Детерминированные конечные автоматы. Тема 3

1. Детерминированные конечные автоматы

Детерминированный конечный автомат
(Finite State Machine) - (X, Q, q0, QF, p)
• X = {a1,…an} - конечный алфавит
• Q – конечное множество состояний
• QF Q – множество заключительных
состояний
• q0 Q – начальное состояние
• p : Q Xk Q (X {L,R,H})k –
программа

2. Пример

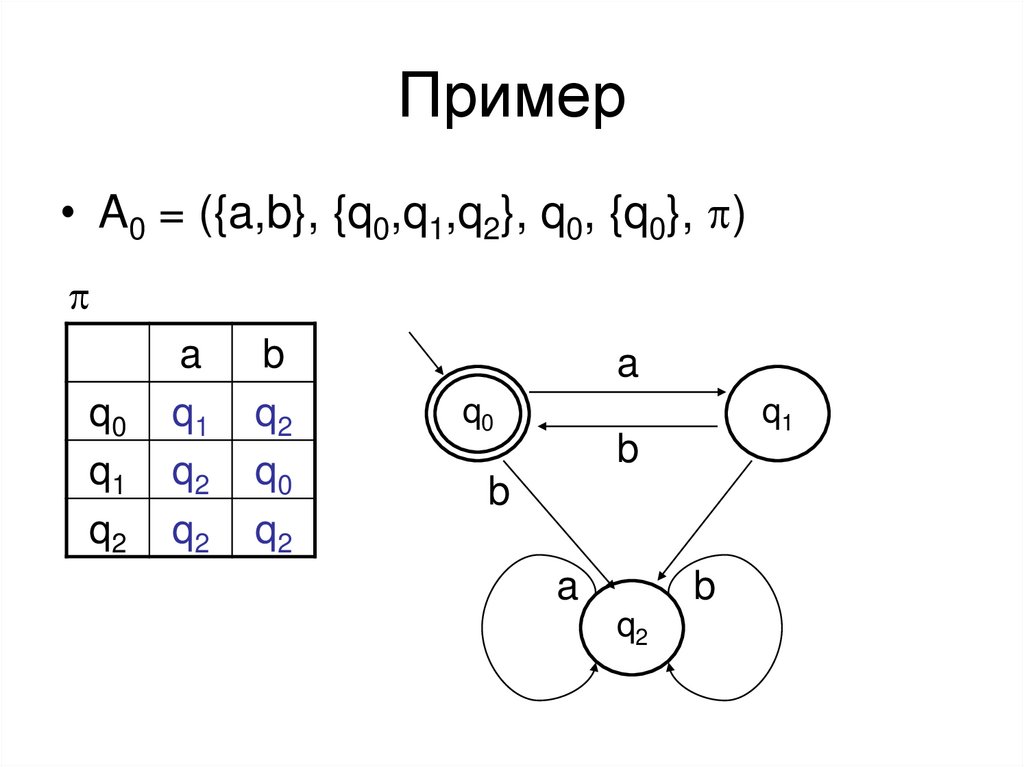
• A0 = ({a,b}, {q0,q1,q2}, q0, {q0}, p)
p
q0
q1
q2
a
q1
q2
q2
b
q2
q0
q2
a
q0
q1
b
b
a
b
q2

3. Язык ДКА

• Язык А - множество цепочек
L(A) = { w=x1,…,xk | k 0 &
p(p(… p(q0,x1)…,xk-1),xk) QF}
• Пример.
L(A0) = { (ab)n | n 0 }
• Обозначение:
LДКА – множество
языков,
допускаемых ДКА
a
q0
q1
b
b
a
a
b
q2

4. Регулярные выражения

• Регулярное выражение над X={a1,…,ak}
– , e, ai – регулярные выражения
– a,b – регулярные выражения регулярными
выражениями являются
• (a b) – конкатенация
• (a+b) – альтернатива
• (a)* - итерация
– других нет
• Приоритет операций: по убыванию *, , +
– Конкатенацию и лишние скобки можно опускать.

5. Регулярные выражения: пример

(((b+e) (((a (a)*) b))*) (a)*)
Эквивалентно
(b+e)(aa*b)*a*

6. Язык регулярного выражения

• L(a,b) X*
– L( ) =
– L(e) = {e}
– L(ai) = {ai}
– L(ab) = { w1w2 | w1 L(a) & w2 L(b) }
– L(a+b) = L(a) L(b)
– L(a*) = e L(a) L(aa) …. – (бесконечное
объединение множеств)
• Множество L регулярно, если L = L(a) для
некоторого a
• Обозначение: Lрег – множество регулярных
языков

7. Недетерминированные конечные автоматы

Недетерминированный конечный
автомат - (X, Q, q0, QF, p)
• X = {a1,…an} - конечный алфавит
• Q – конечное множество состояний
• QF Q – множество заключительных
состояний
• q0 Q – начальное состояние
• p : Q (X e) 2Q – программа

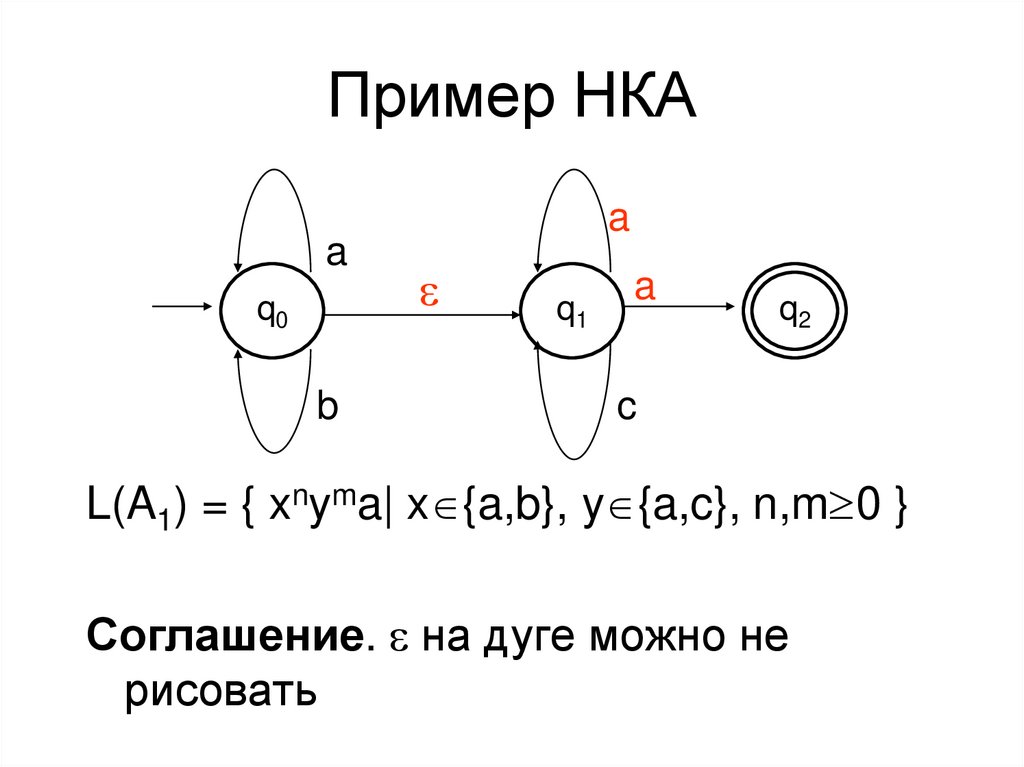
8. Пример НКА

a
q0
b
a
e
q1
a
q2
c
L(A1) = { xnyma| x {a,b}, y {a,c}, n,m 0 }
Соглашение. e на дуге можно не
рисовать

9. Язык НКА

• Обозначение. Если S Q, то
p(S,x) = q S p(q,x)
• Определение. e–замыкание состояния q
qe = { q’ | $ q1,…qk : q1=q & qk=q’
& qi+1 p(qi,e) при i=1..k-1 }
• Неформально: qe – все состояния, включая само q, в
которые можно попасть из q по e–переходам.
• Эквивалентное определение: qe – минимальное
множество, содержащее
{q} p(qe,e)
• Обозначение. Если S Q, то
Se = q S qe

10. Язык НКА

• Язык недетерминированного конечного
автомата А
L(A) = { w=x1,…,xk | k 0 & $ Q1,…,Qk Q :
Q1=q0e & Qk QF
& Qi+1=p(Qi,xk)e при i=1..k-1 }
• Обозначение: LНКА – множество языков,
допускаемых НКА

11. Теорема

Теорема. LНКА = LДКА = Lрег
Доказательство. Докажем
последовательно включения
1. Lрег LНКА
2. LНКА LДКА
3. LДКА Lрег

12. Lрег Н LНКА - структурная индукция

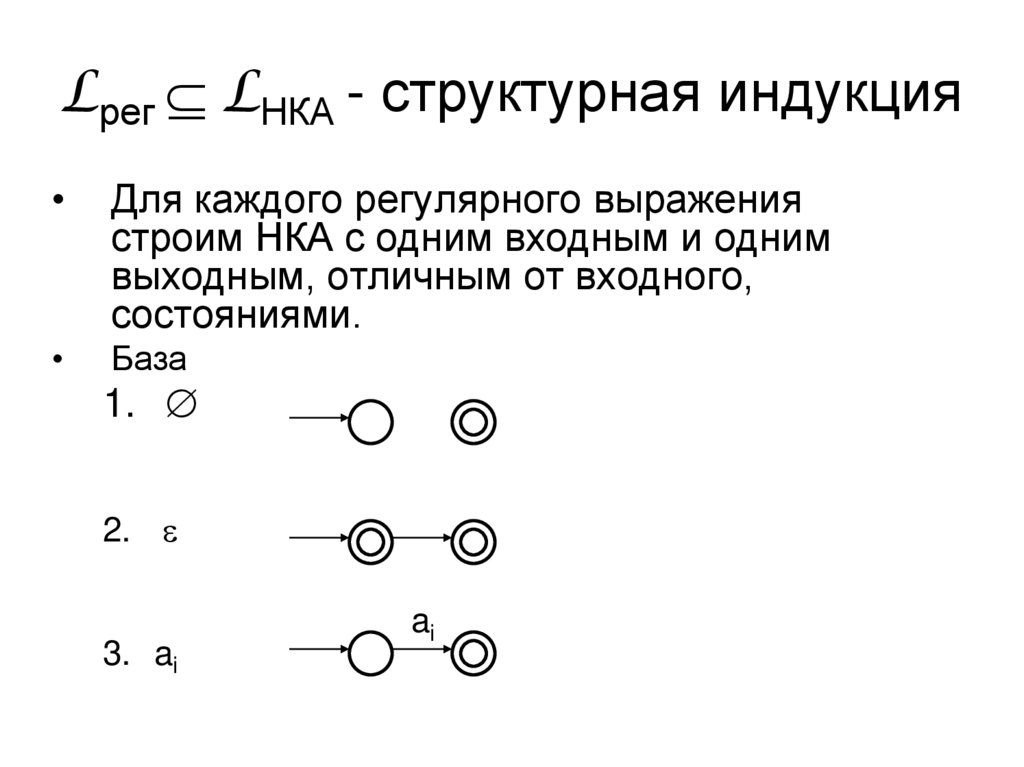
Lрег LНКА - структурная индукция
Для каждого регулярного выражения
строим НКА с одним входным и одним
выходным, отличным от входного,
состояниями.
База
1.
2. e
3. ai
ai

13. Lрег Н LНКА - структурная индукция

Lрег LНКА - структурная индукция
a
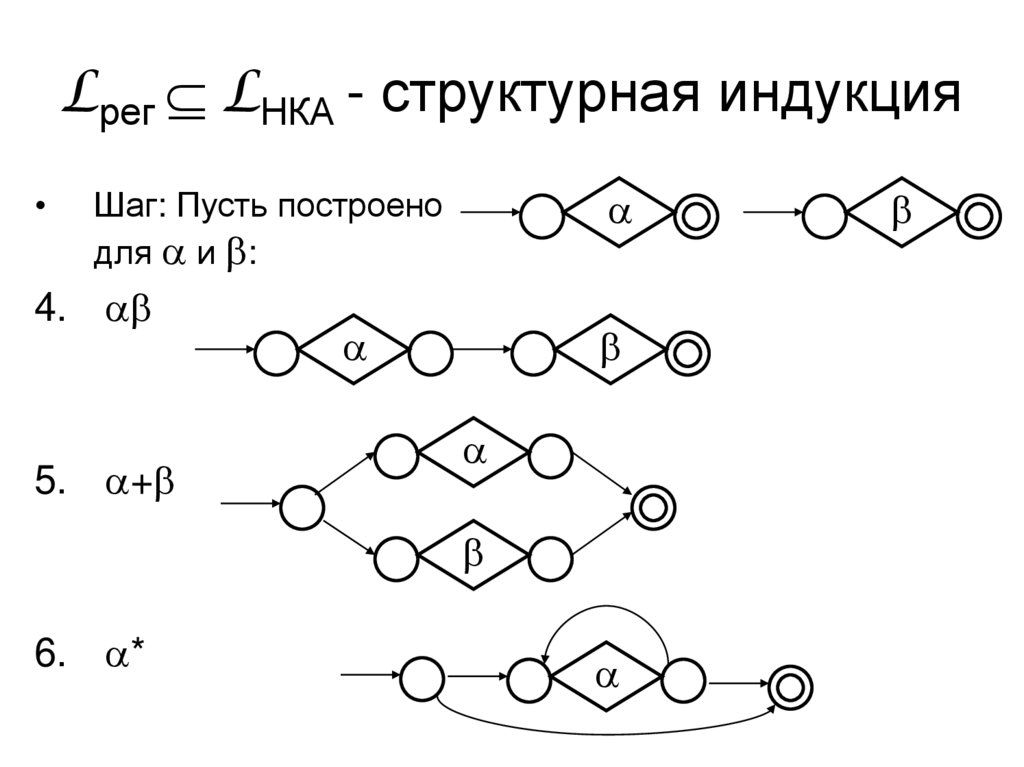
Шаг: Пусть построено
для a и b:
4. ab
5. a+b
a
b
a
b
6. a*
a
b

14. Lрег Н LНКА–пример (b+e)(aa*b)*a*

Lрег LНКА–пример (b+e)(aa*b)*a*
b
a
a
b
a

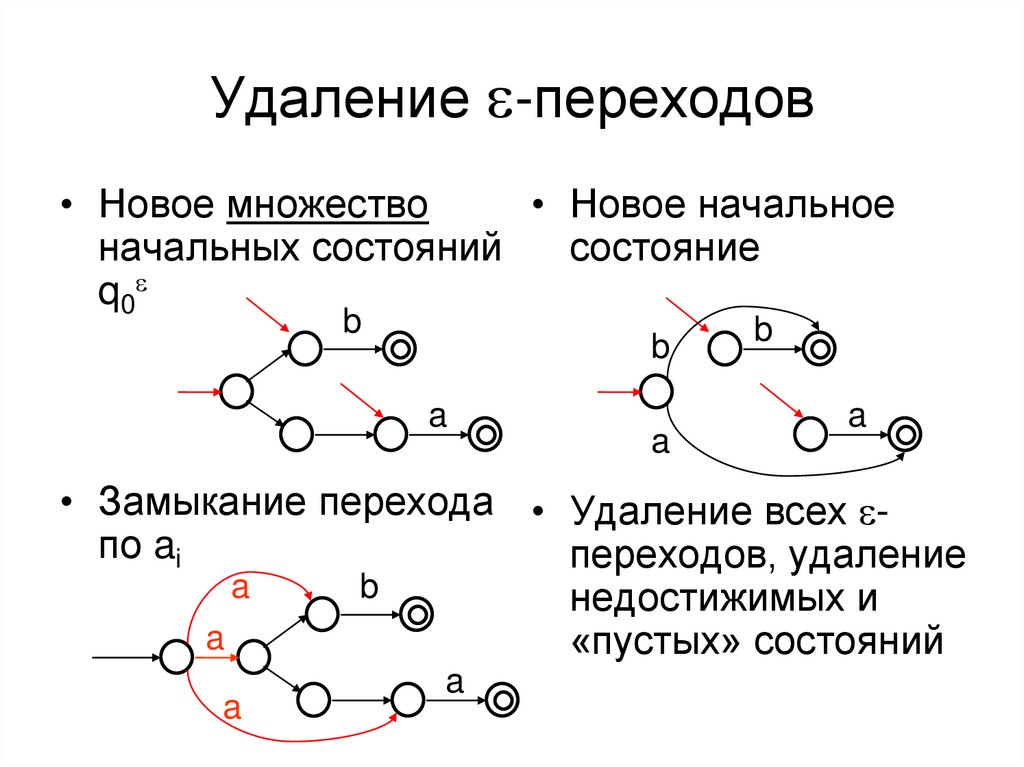
15. Удаление e-переходов

• Новое множество
• Новое начальное
начальных состояний
состояние
q 0e
b
b
a
a
b
a
• Замыкание перехода • Удаление всех eпо ai
переходов, удаление
a
b
недостижимых и
a
«пустых» состояний
a
a

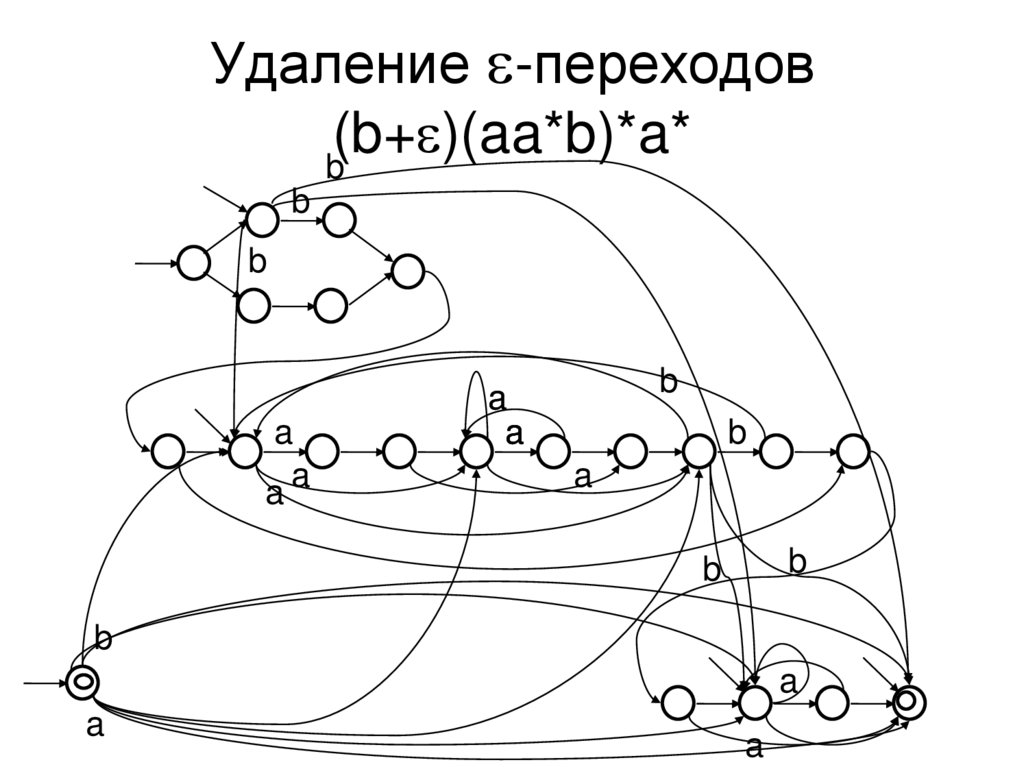
16. Удаление e-переходов (b+e)(aa*b)*a*

b
b
b
a
aa
b
a
a
b
a
b
b
b
a
a
a

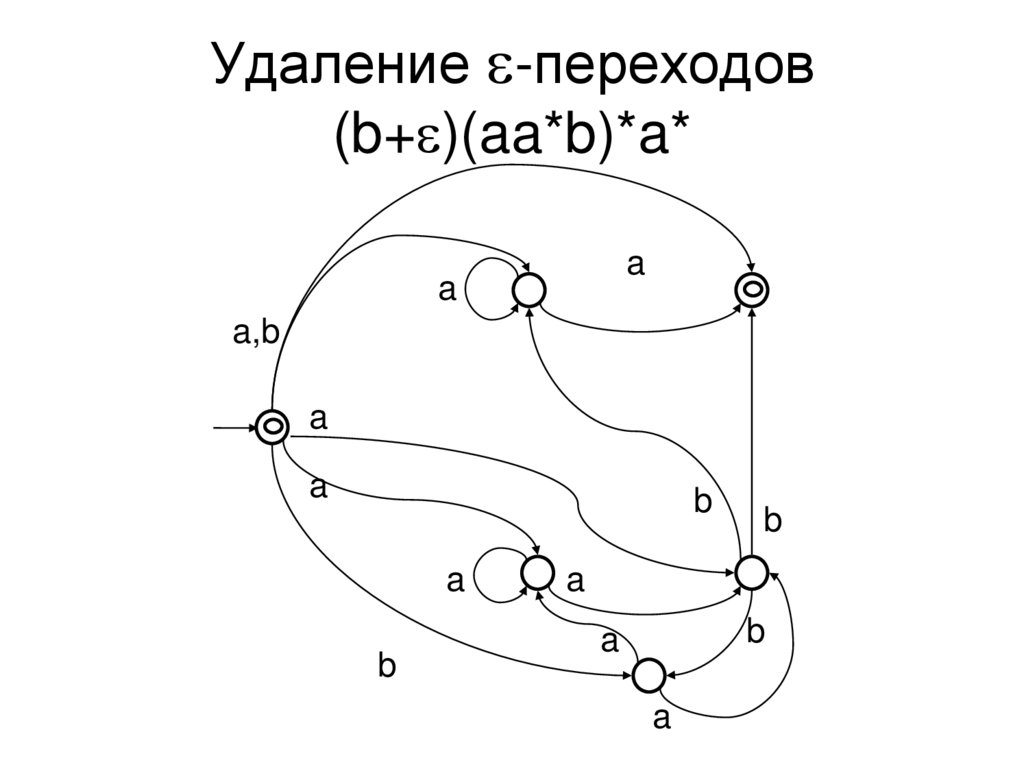
17. Удаление e-переходов (b+e)(aa*b)*a*

a
a
a,b
a
a
b
a
b
b
a
b
a
a

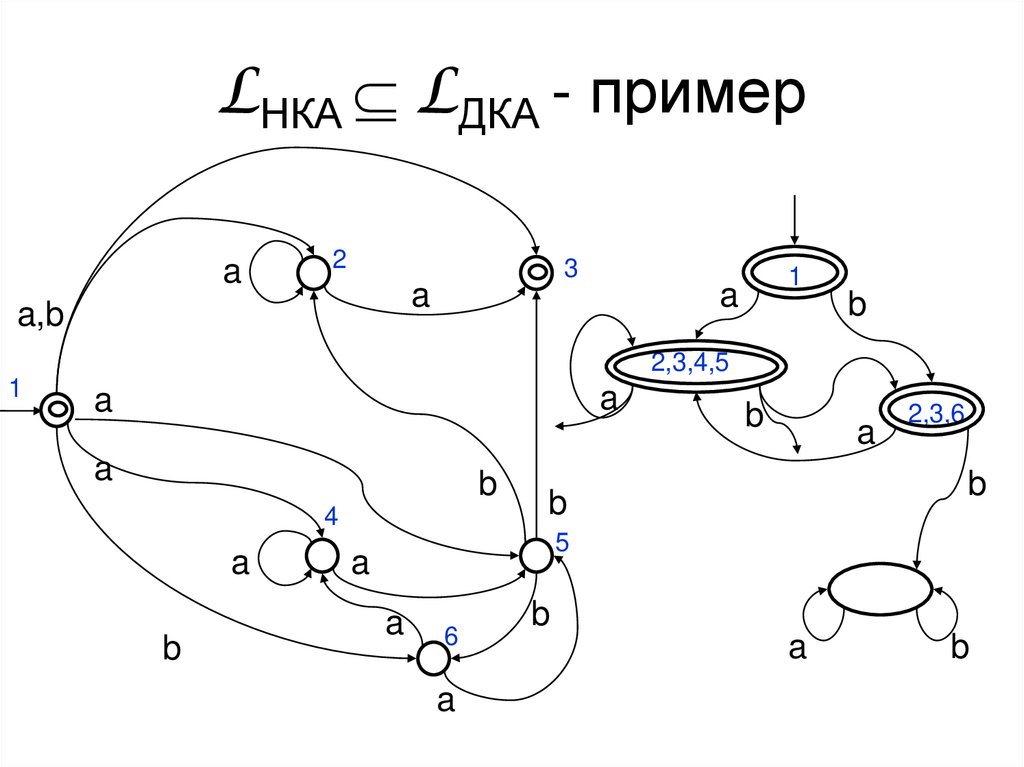
18. LНКА Н LДКА

LНКА LДКА
• Пусть A=(X, Q, q0, QF, p) – НКА.
• Определим A’= (X, 2Q, q0e, QF’, p’)
– QF’ = { S 2Q | S QF }
– p’(S,a) = p(S,x)e
• Индукция по длине w=x1,…,xk
– Пусть q1,…,qk Q такие, что
q1=q0 & qi+1 p(qi,xi+1) при i=1..k-1
– Тогда существуют Q1,…,Qk Q, такие что
Q1=q0e & Qi+1 p’(Qi,xi+1)e при i=1..k-1
– и qi Qi
• И аналогично обратное

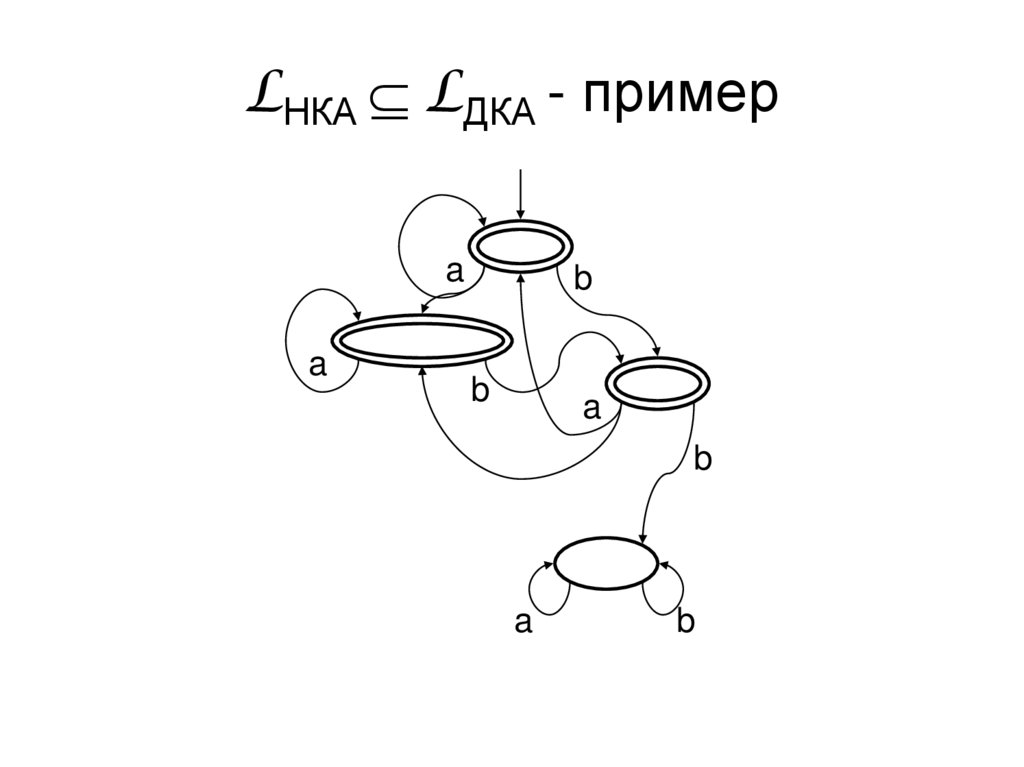
19. LНКА Н LДКА - пример

LНКА LДКА - пример
a
2
3
a
a,b
1
a
b
2,3,4,5
1
a
a
a
b
4
a
b
b
a
2,3,6
b
b
5
a
a
6
a
b
a
b

20. LНКА Н LДКА - пример

LНКА LДКА - пример
a
a
b
b
a
b
a
b

21. LДКА Н Lрег

LДКА Lрег
• Пусть A=(X, Q, q0, QF, p) – ДКА.
– Q = {q1,…,qn}
• Обозначим
– Lij - множество слов по всем путям от qi к qj
– Lijk - множество слов по всем путям от qi к qj
с промежуточными состояниями {q1,…,qk}
– Построим Rijk – регулярное выражение,
такое что L(Rijk) = Lijk.

22. Построение Rijk (индукция по k)

• k = 0) Пусть B = { b X | qj =
p(qi,b) } = {b1,…,bm}
qi
– i j
• Rij0 = , если m=0
• Rij0 = b1 + … + bm, если
m>0
– i=j
• Rij0 = e, если m=0
• Rij0 = e + b1 + … + bm, если
m>0
b1
b2
qj
…
bm
b1
bm…
qi
b2

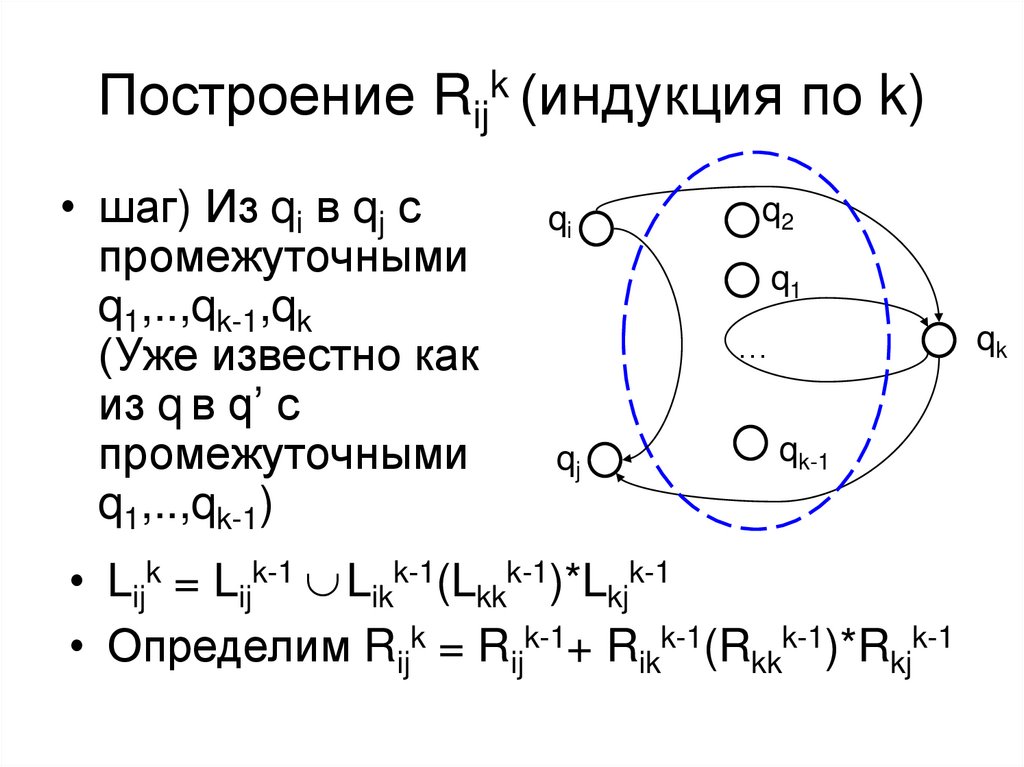
23. Построение Rijk (индукция по k)

• шаг) Из qi в qj с
промежуточными
q1,..,qk-1,qk
(Уже известно как
из q в q’ с
промежуточными
q1,..,qk-1)
qi
q2
q1
qk
…
qj
qk-1
• Lijk = Lijk-1 Likk-1(Lkkk-1)*Lkjk-1
• Определим Rijk = Rijk-1+ Rikk-1(Rkkk-1)*Rkjk-1

24. LДКА Н Lрег

LДКА Lрег
• Пусть q0=qs, s 1..n
• Пусть (без ограничения общности)
QF = {q1,q2,…,qf}
• Тогда R = Rs1 + Rs2 + … + Rsf
• Конец доказательства.

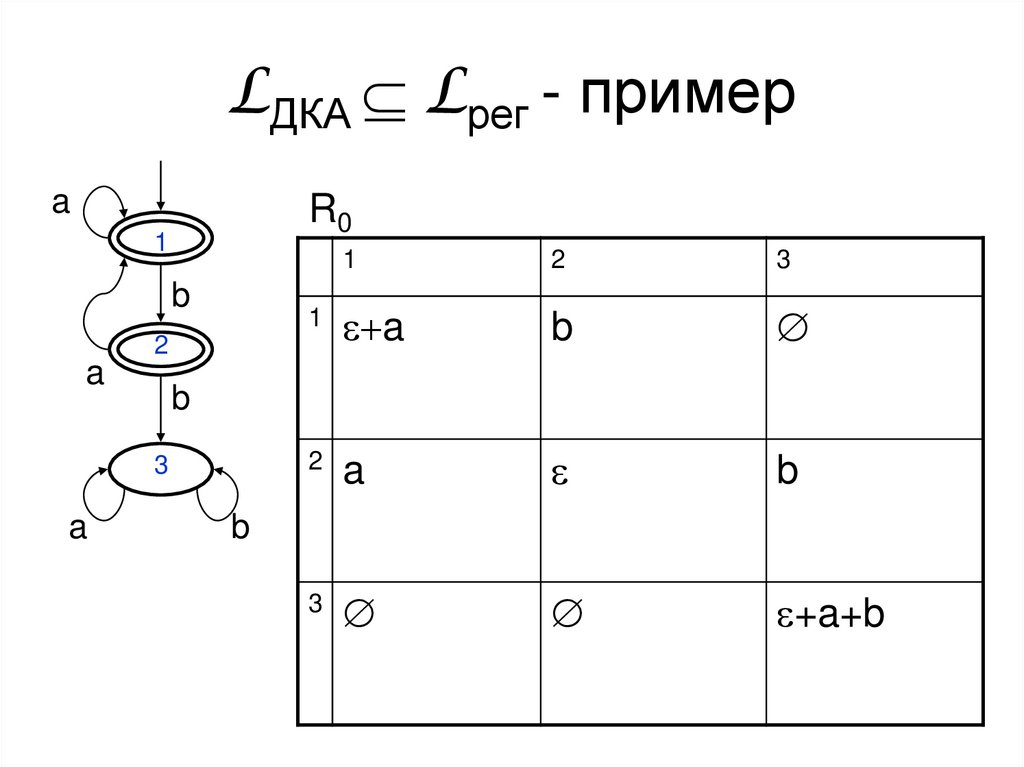
25. LДКА Н Lрег - пример

LДКА Lрег - пример
a
R0
1
b
1
2
3
1
e+a
b
2
a
e
b
3
e+a+b
2
a
b
3
a
b

26. LДКА Н Lрег - пример

LДКА Lрег - пример
R0
R1
1
2
3
1
e+a
b
2
a
e
b
3
e+a+b
1
2
3
e+a+
(e+a)
(e+a)*
(e+a)
2
a+a
(e+a)*
(e+a)
b+
(e+a)
(e+a)*b
+ (e+a)
(e+a)*
e+a
(e+a)*b
b+a
(e+a)*
+
(e+a)*
(e+a)
+
(e+a)*b
e+a+b+
(e+a)*
1
3
Rijk = Rijk-1+ Rikk-1(Rkkk-1)*Rkjk-1

27. LДКА Н Lрег - пример

LДКА Lрег - пример
R1
R2
1
2
1
a*
a*b
2
aa* e+a b
a*b
3
3
e+a
+b
Rijk = Rijk-1+ Rikk-1(Rkkk-1)*Rkjk-1
1
2
3
a*+a*b
a*b+a*b +a*b
(e+aa*b)* (e+aa*b)* (e+aa*b)*
aa*
(e+aa*b) b
2
aa*+(e+a e+aa*b+( b+(e+aa*
a*b)
e+aa*b) b)
(e+aa*b)* (e+aa*b)* (e+aa*b)*
aa*
(e+aa*b) b
3
+ ...
+ ...
e+a+b+
...
1

28. LДКА Н Lрег - пример

LДКА Lрег - пример
R3
1
...
• R113+ R123 =
a*+a*b R22aa*
+ a*bR22
(aa*b)*
…
• R22 = (aa*b)*
...
...
2
1
a*+a*b(aa* a*b(aa*b)*
b)*aa*
2
(aa*b)*aa*
3
...
3

29. LДКА Н Lрег - пример

LДКА Lрег - пример
• R113 =
= a*+a*b R22aa* + a*bR22 =
= a* + a*bR22(e+aa*) =
= a* + a*bR22a* =
= a* + a*b(aa*b)*a*
• Конец примера.

30. Лемма о разрастании (Pumping theorem)

• Лемма. Если L – бесконечный
регулярный язык, то $ a,b, X*, b e :
"n 0 : abn L.
• Доказательство.
– Поскольку L - регулярный, то существует A
– ДКА, L=L(A).
– Поскольку L – бесконечный, то существует
w=x1,…,xk, такое что w L и k>|QA|

31. Доказательство

– Тогда в последовательности состояний
q0=q1,…,qk QF, qi+1=p(qi,xi), cуществует
повторение:
qb=qe, где e>b
– Тогда искомые цепочки:
• a =x1,…,xb-1
• b = xb,…,xe-1
• = xe,…,xk
q1
x1
xe-1
xb-1
qb=qe
• Конец доказательства.
xb
xe
xk
qk

32. Пример

L = {anbn | n>=0} – не регулярный.
• Предположим противное. Тогда по лемме $
a,b, X*, b e : "n 0: abn = anbn.
– b=aaa…a, тогда при повторении b количество a
будет больше b
– b = bbb…b, тогда при повторении b количество a
будет больше b
– b = ...a…b…, тогда при повторении b появится
вхождение a после b.
• Противоречие.

33. Проблема пустоты

• Автомат A пуст, если L(A)=
• Распознавание пустоты:
– Пусть A= (X, Q, q0, QF, p)
– L(A)= , если QF - недостижимо из q0.
– Сложность:O(|Q|)

34. Проблема эквивалентности

Автоматы A и B эквивалентны (A B), если
L(A)=L(B)
Распознавание эквивалентности - 4 способа:
1. Перебор всех цепочек (вплоть до определённой
длины)
2. Алгебраический (сведение к проблеме пустоты)
3. Построением минимального автомата
(канонической формы)
4. Сведение к задаче «Объединить-найти» (почти
линейное время)

35. 1. Перебор всех цепочек

• Теорема. Пусть A1 и A2 – ДКА. Если A1
и A2 не эквивалентны, то $ w L(A1)
L(A2) : |w| |QA1| |QA2|.
• Доказательство.
– Если A1 и A2 не эквивалентны, то $
w L(A1) L(A2) . Пусть w=x1,…,xn, n>
|QA1| |QA2|.
– Тогда в последовательности пар (q11, q12),
…, (qn1, qn2), q1k=q0k, qi+1k = pA(qik,xi) есть
повторение.

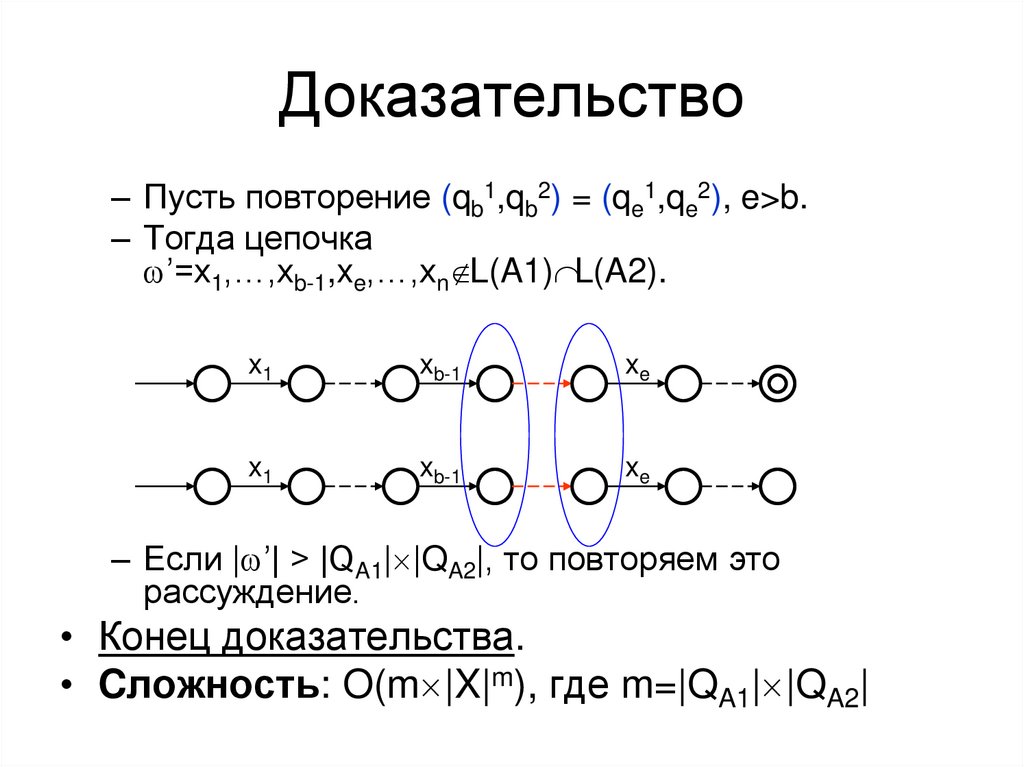
36. Доказательство

– Пусть повторение (qb1,qb2) = (qe1,qe2), e>b.
– Тогда цепочка
w’=x1,…,xb-1,xe,…,xn L(A1) L(A2).
x1
xb-1
xe
x1
xb-1
xe
– Если |w’| > |QA1| |QA2|, то повторяем это
рассуждение.
• Конец доказательства.
• Cложность: O(m |X|m), где m=|QA1| |QA2|

37. 2. Алгебраический (сведение к проблеме пустоты)

• Определим набор операций над
автоматами так, что для каждой
операции язык результата выражается
через язык аргументов
• Построим с помощью этих операций по
автоматам A1 и A2 автомат A такой, что
A пуст тогда и только тогда, когда A1
эквивалентен А2

38. 2. Алгебраический (сведение к проблеме пустоты)

• Отрицание А=(X, Q, q0, QF, p)
– A = (X, Q, q0, Q\QF, p)
– Очевидно, что L( A) = X* \ L(A)
• Произведение Аi=(X, Qi, q0i, QFi, pi), i=1,2
– А1 А2 = (X, Q1 Q2, (q01,q02), QF1 QF2, p), где
p((q1,q2),a) = (p1(q1,a), p2 (q2,a))
– Простой индукцией: L(А1 А2) = L(А1) L(А2)
• Сумма: Аi=(X, Qi, q0i, QFi, pi), i=1,2
– А1+А2 = (X, Q1 Q2, (q01,q02), QF, p), где
p((q1,q2),a) = (p1(q1,a), p2 (q2,a)),
QF= {(q1,q2) | q1 Q1 q2 Q2}
– Простой индукцией: L(А1 А2) = L(А1) L(А2)

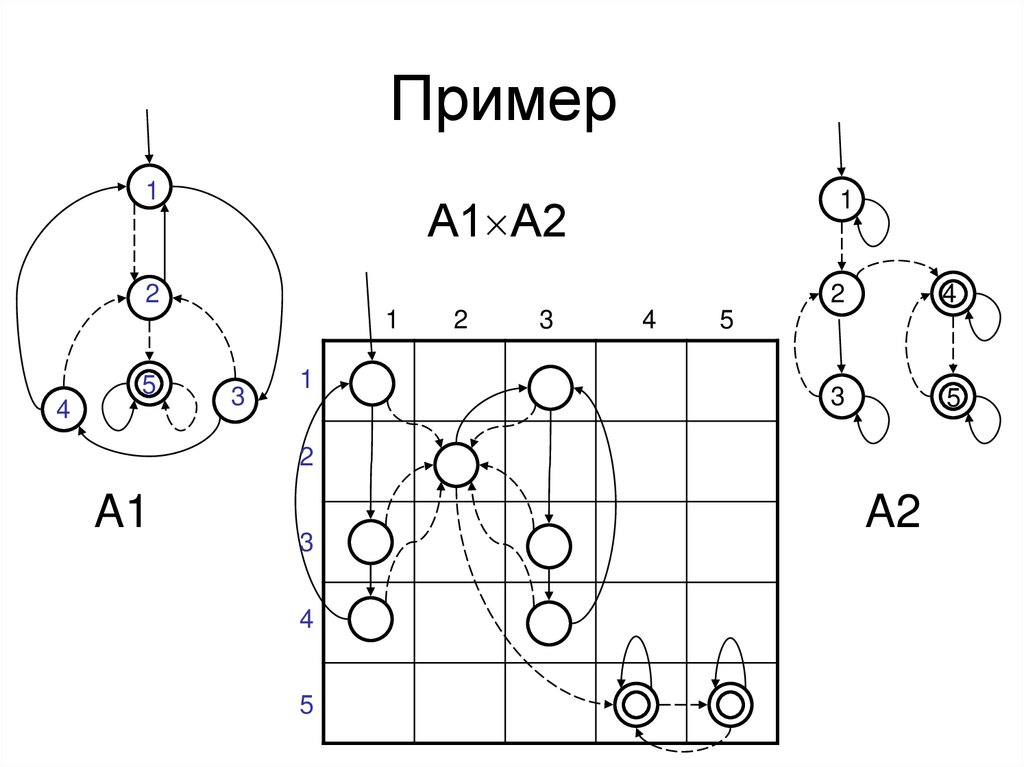
39. Пример

1
1
А1 А2
2
1
5
4
3
1
2
3
4
2
4
3
5
5
2
A1
3
4
5
A2

40. 2. Алгебраический (сведение к проблеме пустоты)

• Рассмотрим автомат
A = А1 А2 + А2 А1
• L(A) = L(А1 А2) L(А2 А1) =
= L(А1) L( А2) L(А2) L( А1) =
= L(А1) (X* \ L(А2)) L(А2) (X* \ L(А1)) =
= (X* L(А1) \ L(А1) L(А2)) …
= L(А1) \ L(А2) L(А2) \ L(А1)
• Cложность:
– Построение А: O(|Q1| |Q2|)
– Проверка пустоты: O(|QA|)

41. 3. Построением минимального автомата

• Пусть Аi=(X,Qi,q0i,QFi, pi), i=1,2.
Cостояния q1 Q1 и q2 Q2 эквивалентны
(q1 q2), если
(X, Q1, q1,QF1,p1) (X,Q2,q2,QF2,p2)
• Автомат минимален, если
– нет недостижимых состояний
– нет эквивалентных состояний

42. 3. Построением минимального автомата

• Теорема. Если A1 и A2 минимальны и
эквивалентны, то A1 и A2 изоморфны.
• Доказательство.
– Пусть А равен A1 A2, в котором удалены
все недостижимые
– Покажем, что "q1 Q1 $! (q1,q2) QA: q1 q2.
(Наоборот - аналогично.)

43. Доказательство

– Поскольку q1 Q1 достижима в A1, то существует
q2 Q2 такое, что (q1,q2) достижима в A1 A2, т.е.
(q1,q2) QA
– Если (q1,q2) QA, то q1 q2, так как иначе
существовали бы w, w’ X* такие, что w «ведёт» от
(q01,q02) к (q1,q2), а w’ – от (q1,q2) к (q’1,q’2) QF1 QF2,
что означало бы неэквивалентность q01 и q02.
– Если (q1,q2), (q1,q’2) QA, то q2=q’2, поскольку в A2
нет эквивалентных.
• Конец доказательства.

44. Грубейшее разбиение

Утверждение: q1 q2 тогда и только тогда,
когда
–
–
{q1,q2} QF {q1,q2} Q\QF –
(любое заключительное состояние не
эквивалентно любому незаключительному)
" a X : p(q1,a) p(q2,a) –
(q1 и q2 не эквивалентны, если существует a X
такое, что p(q1,a) и p(q2,a) не эквивалентны)
Задача: разбить QF=S1 … Sk и
Q\QF=Sk+1 … Sm на минимальное
количество непересекающихся
подмножеств, удовлетворяющих указанным
условиям

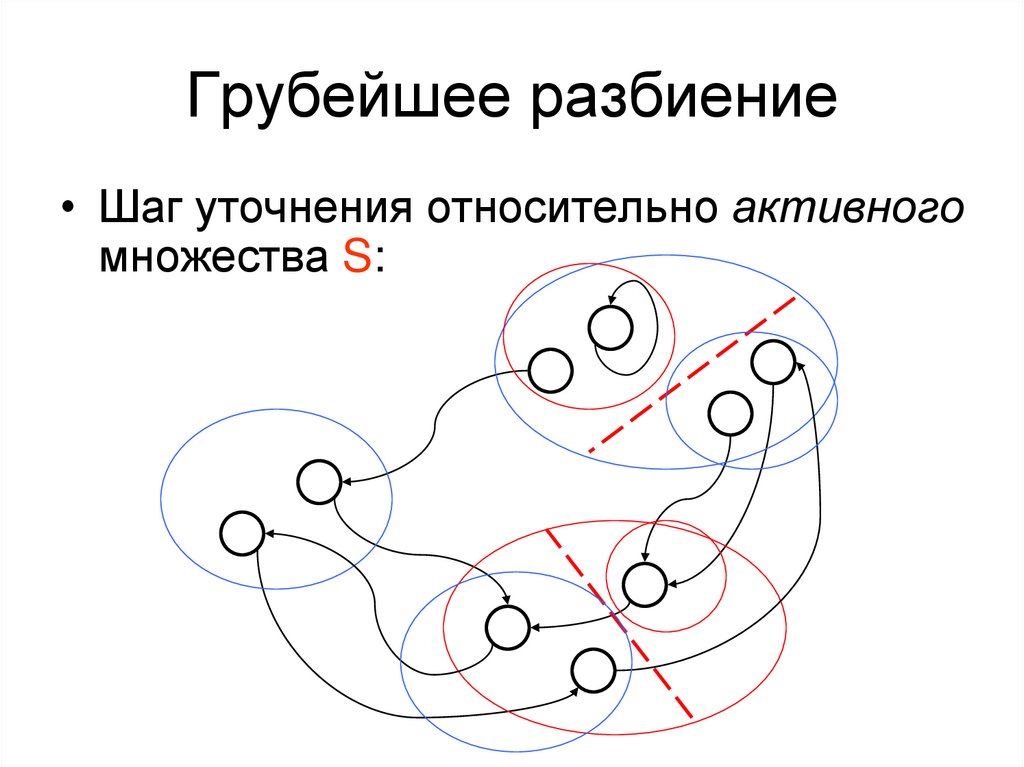
45. Грубейшее разбиение

• Шаг уточнения относительно активного
множества S:

46. Грубейшее разбиение

• Сложность (неформальные
рассуждения):
– При каждом расщеплении размер
активного множества убывает по крайней
мере в два раза
– Собственно расщепление – за линейное
время
– Проверка изоморфизма: O(max(|Q1|,|Q2|))
– Итого: O(n log(n))
(Подробнее – реферат на семинаре.)

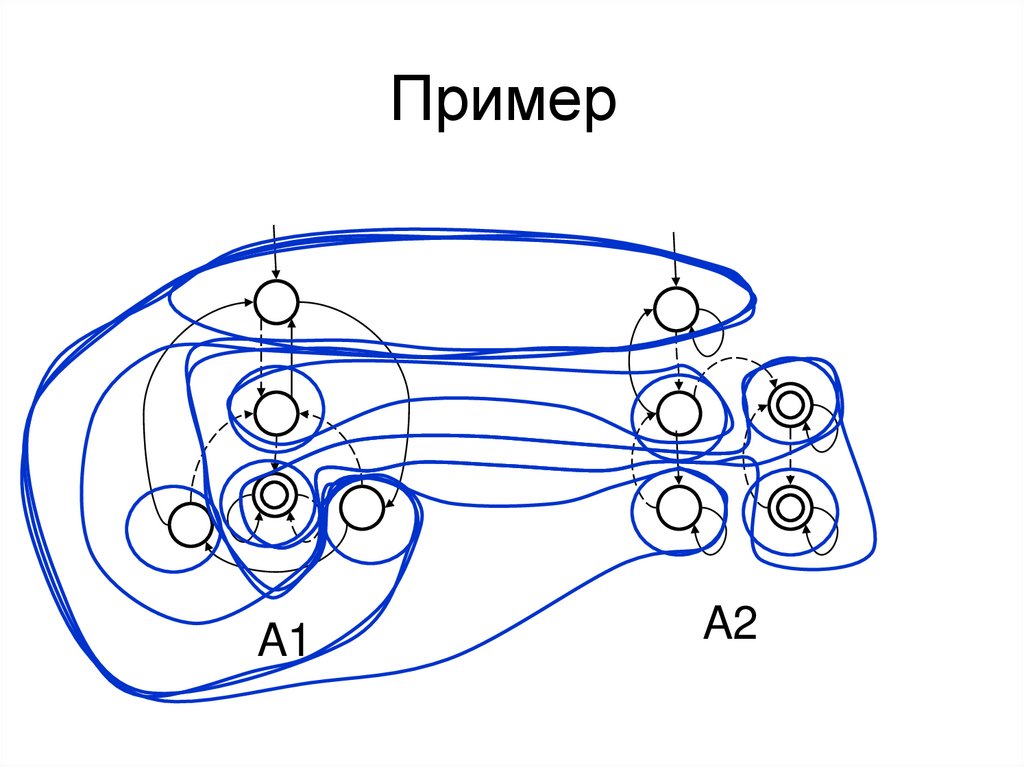
47. Пример

4. Сведение к задаче
«Объединить-найти»
• Изначально не эквивалентны все, за
исключением q01 и q02
• Если q1 q2, то объявляем p(q1,a) p(q2,a)
• Если объявили эквивалентными q1 –
заключительное и q2 – не
заключительное (или наоборот), то
автоматы не эквивалентны

48. 4. Сведение к задаче «Объединить-найти»

Пример
A1
A2

49. Пример

4. Сведение к задаче
«Объединить-найти»
• Актив := (q01, q02);
• Набор := { {q} | q Q1 Q2 }
• Пока $(q1,q2) Актив
– удалить (q1,q2) из Актив
– М1:=Найти(q1), M2:= Найти(q2)
– Если М1 М2 то
• Объединить(М1,М2,М1)
• Для всех a X
–Добавить (p(q1,a),p(q2,a) в Актив

50. 4. Сведение к задаче «Объединить-найти»

• Сложность. O(nG(n))
G(n) = min { k | F(k) n}
– F(0) = 1
– F(k) = 2F(k-1)
0
1
2
3
4
5
1
2
4
16
65536 265536
• G(n) 5 при n 265536
• (Подробнее – реферат на семинаре.)