Similar presentations:
Неоднозначные языки
1. Неоднозначные языки
Язык, порождаемый грамматикой неоднозначный, если он не можетбыть порожден никакой однозначной грамматикой.
Проблема определения, порождает ли данная КС-грамматика
однозначный язык (т.е. существует ли эквивалентная ей однозначная
грамматика), является алгоритмически неразрешимой.
Пример неоднозначного КС-языка:
L = {ai bj ck | i = j или j = k} .
Одна из грамматик, порождающих L, такова:
S → AB | DC
( док-во для цепочки abc )
A → aA |
B → bBc |
C → cC |
D → aDb |
1
2. Бесплодные символы грамматики
Символ A N является бесплодным в грамматике G = (T, N, P, S),если множество { T* | A } пусто.
Алгоритм удаления бесплодных символов:
Вход:
КС-грамматика G (T, N, P, S ),
Выход:
КС-грамматика G' (T, N', P', S ), не содержащая
бесплодных символов, для которой L(G) = L(G').
Метод:
Строим множества N0, N1, ...
1. N0 : ; i : 1.
2. Ni : Ni − 1 { A | A → P и (T Ni − 1 ) } .
Если Ni Ni − 1, то i : i + 1 и переходим к шагу 2,
иначе N' : Ni ; P' состоит из правил множества P,
содержащих только символы из Ni T ; G' : (T, N', P', S).
2
3. Удаление бесплодных символов грамматики. Пример.
S → AC | Bb |A → aCb
B → bB
C → cCc | c
D → Aa | Bb | d
Шаг 0:
Шаг 1:
Шаг 2:
Шаг 3:
N0 : ; i : 1.
N1 : {S, C, D}; i : 2.
N2 : {S, C, D, A}; i : 3.
N3 : {S, C, D, A} = N2, т.е. искомое множество построено.
Удаляем все правила, содержащие нетерминал B, не вошедший в
построенное множество:
S → AC |
A → aCb
C → cCc | c
D → Aa | d
3
4. Недостижимые символы грамматики
Символ x (T N) является недостижимым в грамматикеG = (T, N, P, S), если он не появляется ни в одной сентенциальной
форме этой грамматики.
Алгоритм удаления недостижимых символов:
Вход:
КС-грамматика G (T, N, P, S ),
Выход:
КС-грамматика G' (T', N', P', S ), не содержащая
недостижимых символов, для которой L(G) = L(G').
Метод:
Строим множества V0, V1, ...
1. V0 : {S }; i : 1.
2. Vi : Vi − 1 { x | x T N,
A → x P, A Vi − 1, , (T N ) } .
Если Vi Vi − 1, то i : i + 1 и переходим к шагу 2,
иначе N' : Vi N ; T' : Vi T ; P' состоит из правил множества P, 4
содержащих только символы из Vi ; G' : (T', N', P', S).
5. Удаление недостижимых символов грамматики. Пример
S → AC |A → aCb
C → cCc | c
D → Aa | d
Шаг 0:
Шаг 1:
Шаг 2:
Шаг 3:
V0 : {S}; i : 1.
V1 : {S, A, C, } { }; i : 2.
V2 : {S, A, C, , a, b, c}; i : 3.
V3 : {S, A, C, , a, b, c} = V2, т.е. искомое множество
построено
Удаляем все правила, содержащие символы D и d, не вошедшие в
построенное множество:
S → AC |
A → aCb
C → cCc | c
5
6. Приведенные грамматики
Недостижимые и бесплодные символы в грамматике G = (T, N, P, S)называются бесполезными символами в этой грамматике.
КС-грамматика G называется приведенной, если в ней нет
бесполезных символов.
Алгоритм приведения грамматики:
1)
2)
обнаруживаются и удаляются все бесплодные нетерминалы.
обнаруживаются и удаляются все недостижимые символы.
Удаление символов сопровождается удалением правил вывода,
содержащих эти символы.
Если в алгоритме переставить шаги 1) и 2), то не всегда результатом
будет приведенная грамматика. Например, при такой перестановке шагов
грамматика
S → AB | а
A→ b
B → BA
останется неприведенной.
6
7. Алгоритм устранения правил с пустой правой частью
Вход: КС-гр-ка G (T, N, P, S ).Выход: КС-гр-ка G' (T, N', P', S' ) - неукорачивающая, L(G') L(G).
Метод:
1. Построить множество Х {A N | A } ; N′ : N .
2. Построить P′, удалив из множества правил P все правила
с пустой правой частью.
3. Если S X, то ввести новый начальный символ S′, добавив его в N′,
и в P′ добавить правило S′ S | . Иначе переименовать S в S′.
4. Каждое правило из P′ вида
B → 1A1 2A2... n An n +1,
где Ai X для i 1,..., n, i ( (N′ − X) T )* для i 1,..., n + 1 ,
заменить 2n правилами, соответствующими всем возможным
комбинациям вхождений Аi между i:
B → 1 2... n n + 1 | 1 2... nAn n + 1 | ... | 1 2A2... nAn n + 1 |
1A1 2A2... nAn n + 1
Если i для всех i 1, ..., n + 1, то получившееся правило
B → не включать в множество P′.
5. Удалить бесполезные символы и правила, их содержащие.
7
8. Устранение правил с пустой правой частью. Пример
S → BC | Ab | ABA → Aa |
B→
C→c
Шаг 1:
Шаг 2:
N1 : { A, B };
N2 : { A, B, S };.
S1 → S |
S → BC | C | Ab | b | AB | A | B
A → Aa | a
C→c
Приводим грамматику:
S1 → S |
S → C | Ab | b | A
A → Aa | a
C→c
8
9. Элементы теории трансляции Лексический анализ
В основе лексических анализаторов лежат регулярныеграмматики.
Способы описания регулярных языков:
– регулярные грамматики
(леволинейные или праволинейные)
– конечные автоматы
(недетерминированные или детерминированные)
– регулярные выражения
(см. материал “О регулярных языках” на cmcmsu.info и
методическое пособие по формальным языкам)
9
10. Недетерминированный конечный автомат (НКА)
НКА - это пятерка (K, T, δ , H, S), гдеK - конечное множество состояний;
T - конечное множество допустимых входных символов;
δ - отображение (функция переходов) множества K T в
множество подмножеств K;
H K – множество начальных состояний;
S K – множество заключительных состояний.
δ (A, t) = B означает, что из состояния A по входному символу t
происходит переход в состояние B.
НКА допускает цепочку
a1a2...an , если
δ(H*, a1)=A1; δ(A1, a2)=A2; ... ; δ(An-2, an-1)=An-1; δ(An-1,an)=S*,
где ai T, Aj K, j = 1, 2,..., n-1; i = 1, 2,..., n;
H*– одно из начальных состояний, S*– одно из заключительных
состояний.
Множество цепочек, допускаемых КА, составляет
10
11. Конечные автоматы, диаграммы состояний
Удобным графическим представлением конечных автоматовявляются диаграммы состояний.
Диаграмма состояний (ДС) – неупорядоченный
ориентированный помеченный граф.
Пример . A 1 = {A, B, C, D, E}, {a, b}, , {A, D}, {C, E} ,
где (A,a)=B, (D,a)=E, (B,b)=C, (E,b)=C, (C,b)=C.
ДС:
A a
B b
C
b
D a
Eb
Входящими непомеченными стрелками отмечены начальные вершины
A и D, исходящими – заключительные вершины E и C.
L(A 1) = {abn | n 0}
11
12. Соглашения для работы с диаграммами состояний
a)Если из одного состояния в другое выходит несколько
дуг, помеченных разными символами, то изображается
одна дуга, помеченная всеми этими символами.
a)
Непомеченная
никакими
символами
дуга
соответствует переходу при любом символе, кроме
тех, которыми помечены другие дуги, выходящие из
этого состояния.
a)
Вводится дополнительное состояние ошибки (ER);
переход в это состояние означает, что исходная
цепочка языку не принадлежит.
12
13. Алгоритм построения НКА по леволинейной автоматной грамматике
1. Правило вида А а преобразуется в А Hа, где H – новыйнетерминальный символ, и добавляется правило H ε
2. Множество состояний (вершин) НКА состоит из нетерминалов
преобразованной грамматики.
3. Каждому правилу вида А Bа в автомате соответствует дуга из
состояния В в состояние А, помеченная символом а. Других дуг
нет.
4. Заключительным состоянием автомата является состояние,
соответствующее начальному символу грамматики.
Начальным является каждое состояние A, такое что для
нетерминала A есть правило с пустой правой частью A ε .
13
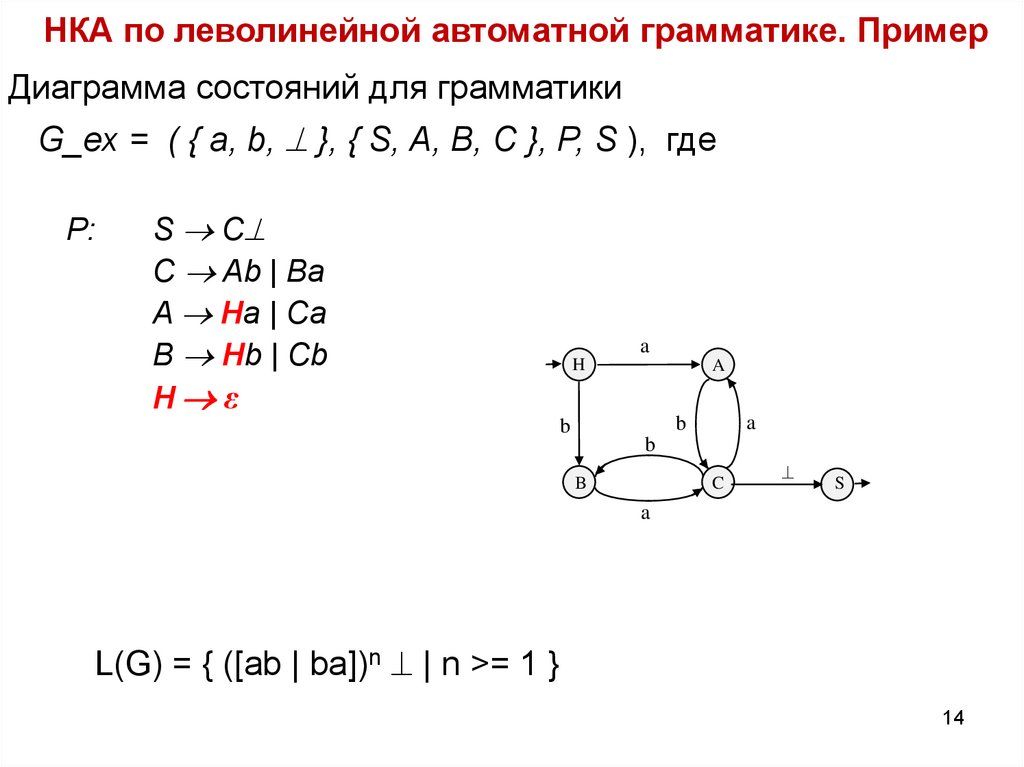
14. НКА по леволинейной автоматной грамматике. Пример
Диаграмма состояний для грамматикиG_ex = ( { a, b, }, { S, A, B, C }, P, S ), где
P:
S C
C Ab | Ba
A Ha | Ca
B Hb | Cb
Н ε
a
H
A
a
b
b
b
B
C
S
a
L(G) = { ([ab | ba])n | n >= 1 }
14
15. Алгоритм построения НКА по праволинейной автоматной грамматике
1. Каждое правило вида А а преобразуется в А аF, где F –новый нетерминальный символ, и добавляется правило F ε
2. Множество состояний (вершин) НКА состоит из нетерминалов
преобразованной грамматики.
3. Каждому правилу вида А аВ в автомате соответствует дуга из
вершины А в вершину В, помеченная символом а. Других дуг нет.
4.
Начальной вершиной автомата является вершина, соответствующая
начальному символу грамматики.
Заключительной является каждая вершина A, такая что для
нетерминала A есть правило с пустой правой частью A ε.
15
16. НКА по праволинейной автоматной грамматике. Пример
Диаграмма состояний для грамматикиG_ex2 = ( { 0, 1, }, { S, B, C }, P, S ), где
P: S 0B
B 1B | 1C | F
C F
F ε
S
0
B
1
1
C
F
L(G) = { 0 1n | n >= 0 }
16
17. Диаграммы состояний инвариантны относительно праволинейных или леволинейных грамматик, по которым они построены!
W t<==>
W Vt <==>
H
V
t
t
W
, где
S
W
W
<==>
W
________________________________________
t
F
W t
<==>
W
, где
S
t
W
V
W tV <==>
W
<==>
W
17
18. Алгоритм построения леволинейной автоматной грамматики по КА с единственным заключительным состоянием
1. Нетерминалами грамматики будут состояния автомата,терминалами – пометки на дугах.
2. Для каждой дуги A
a
B в грамматику добавляется правило
В → Аа. Для каждого начального состояния В в грамматику
добавляется правило В → .
3. Начальным символом будет нетерминал, соответствующий
заключительному состоянию.
(4). К построенной по пунктам 1–3 грамматике можно применить
алгоритм устранения -правил.
18
19. Алгоритм построения праволинейной автоматной грамматики по КА с единственным начальным состоянием
1. Нетерминалами грамматики будут состояния автомата,терминалами – пометки на дугах.
2. Для каждой дуги A
a
B в грамматику добавляется правило
А → Bа. Для каждого заключительного состояния В в
грамматику добавляется правило В → .
3. Начальным символом будет нетерминал, соответствующий
начальному состоянию.
(4). К построенной по пунктам 1–3 грамматике можно применить
алгоритм устранения -правил.
19
20. Детерминированный конечный автомат (ДКА)
НКА называется детерминированным (ДКА), если:имеет единственное начальное состояние, и
любые две дуги, исходящие из одного и того же состояния имеют
различные пометки.
Множество в ДКА можно интерпретировать как
отображение K в множество K.
ДКА допускает цепочку a1a2...an, , если
(H,a1) = A1; (A1,a2) = A2; ... ; (An-2,an-1) = An-1; (An-1,an) = S,
где ai , Aj K, j = 1, 2,..., n-1; i = 1,2,..., n;
H – начальное состояние,
S – одно из заключительных состояний
20
21. Алгоритм разбора по ДКА
1. Объявляем текущим состояние H;2. Многократно (пока не считаем последний символ входной
цепочки) выполняем следующее:
считываем очередной
символ исходной цепочки и переходим из текущего состояния в
другое состояние по дуге, помеченной этим символом.
Состояние, в которое мы при этом попадаем, становится
текущим.
3. Если в результате работы алгоритма прочитана вся
цепочка, на каждом шаге находилась дуга, помеченная
очередным символом анализируемой цепочки, а последний
переход произошел в состояние S, значит исходная цепочка
принадлежит языку.
4. Если на каком-то шаге не нашлось дуги, выходящей из
текущего состояния и помеченной очередным анализируемым
символом или на последнем шаге произошел переход в
состояние, отличное от S, значит исходная
цепочка не
принадлежит языку.
21
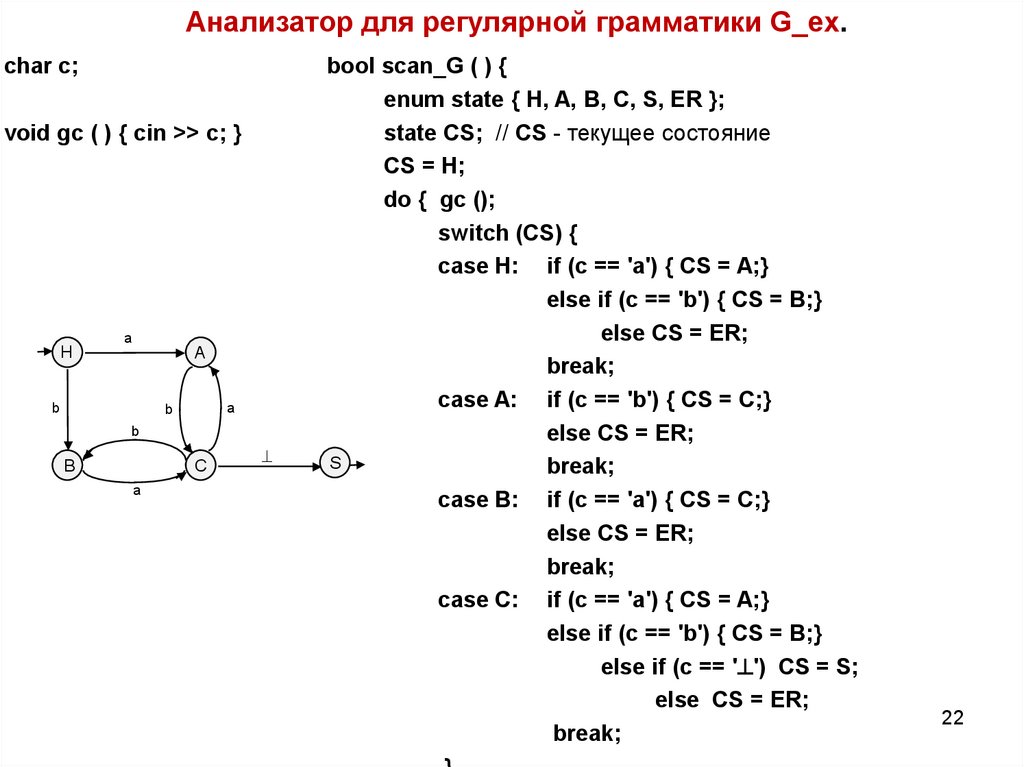
22. Анализатор для регулярной грамматики G_ex.
char c;void gc ( ) { cin >> c; }
H
a
A
b
a
b
b
B
C
a
bool scan_G ( ) {
enum state { H, A, B, C, S, ER };
state CS; // CS - текущее состояние
CS = H;
do { gc ();
switch (CS) {
case H: if (c == 'a') { CS = A;}
else if (c == 'b') { CS = B;}
else CS = ER;
break;
case A: if (c == 'b') { CS = C;}
else CS = ER;
S
break;
case B: if (c == 'a') { CS = C;}
else CS = ER;
break;
case C: if (c == 'a') { CS = A;}
else if (c == 'b') { CS = B;}
else if (c == ' ') CS = S;
else CS = ER;
break;
22
23. О недетерминированном разборе
Разбор по НКА недетерминирован (и неэффективен),если:
автомат имеет несколько начальных состояний, или
из какого-либо состояния НКА выходят несколько дуг,
ведущих в разные состояния, но помеченных одним и
тем же символом.
Для леволинейных грамматик эта ситуация возникает,
когда в правилах вывода есть совпадающие правые
части.
Для праволинейных грамматик аналогичная ситуация
возникает, когда альтернативы вывода из одного
нетерминала грамматики начинаются одинаковыми
терминальными символами.
НО!
Существует
алгоритм
произвольного НКА в ДКА !
преобразования
23
24. Алгоритм построения ДКА по НКА M = (K, T, δ , H, S)
Вход: НКА. Выход: M1 = (K1, T, δ1, H1, S1) – эквивалентный ДКА.Метод:
1. Начальным состоянием Н ДКА объявляем Н1Н2…Нk (каждое Hi –
начальное состояние НКА).
2. Строим отображение δ1 (K1 T → K1) по δ, начиная с состояния H.
3. δ1 для Н К1 :
- если в НКА переход из Н по t детерминирован, переносим
соответствующие отображение в результирующий КА;
- если же в НКА переход из Н по t недетерминирован, то в КА
включаем отображения δ1 по правилу: δ1(H, t) = A1A2...An,
где Ai К, и в НКА есть F(H, t) = Ai для всех 1 <= i <= n
4. Состояния, появляющиеся в правой части отображений δ1
результирующего КА принадлежат К1; для каждого из них строим
отображения δ1 т.о.:
δ1 (A1A2...An, t) = B1B2...Bm, где для каждого 1 <= j <= m в НКА
существует δ (Ai, t) = Bj для каких-либо 1 <= i <= n.
5. Заключительными состояниями построенного детерминированного
24
КА являются все состояния, содержащие S К в своем имени.
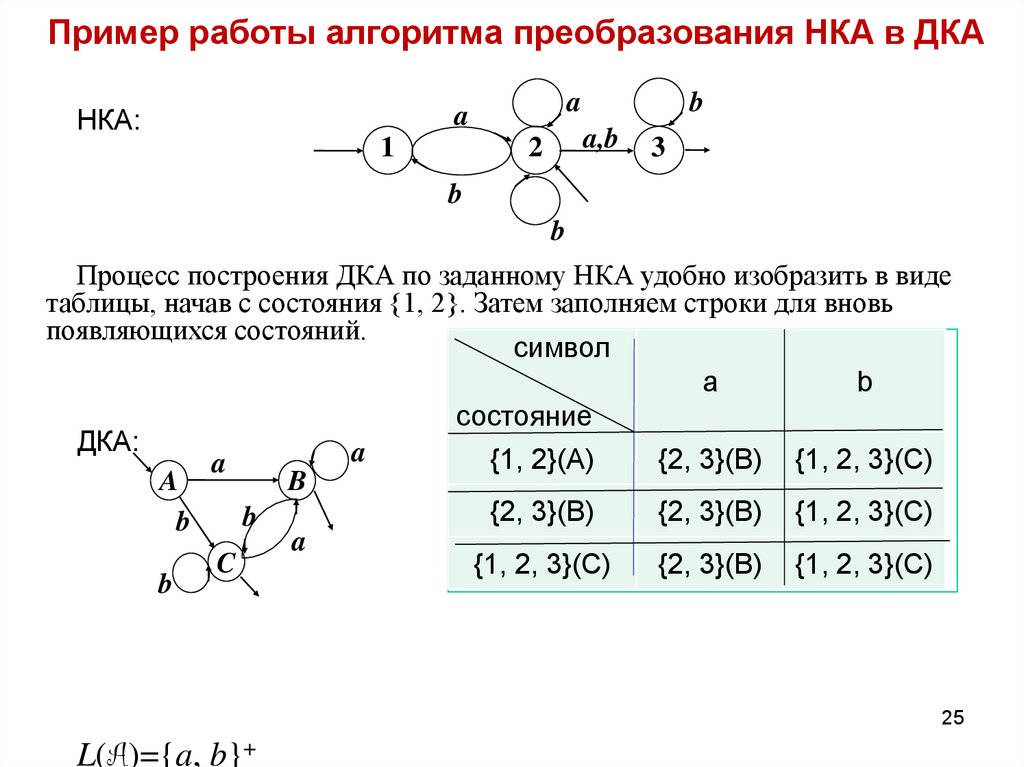
25. Пример работы алгоритма преобразования НКА в ДКА
НКА:a
a
1
b
a,b
2
3
b
b
Процесс построения ДКА по заданному НКА удобно изобразить в виде
таблицы, начав с состояния {1, 2}. Затем заполняем строки для вновь
появляющихся состояний.
символ
a
b
состояние
ДКА:
a
{1, 2}(A)
{2, 3}(B) {1, 2, 3}(C)
a
A
B
{2, 3}(B)
{2, 3}(B) {1, 2, 3}(C)
b
b
a
C
{1, 2, 3}(C)
{2, 3}(B) {1, 2, 3}(C)
b
25
L(A)={a, b}+
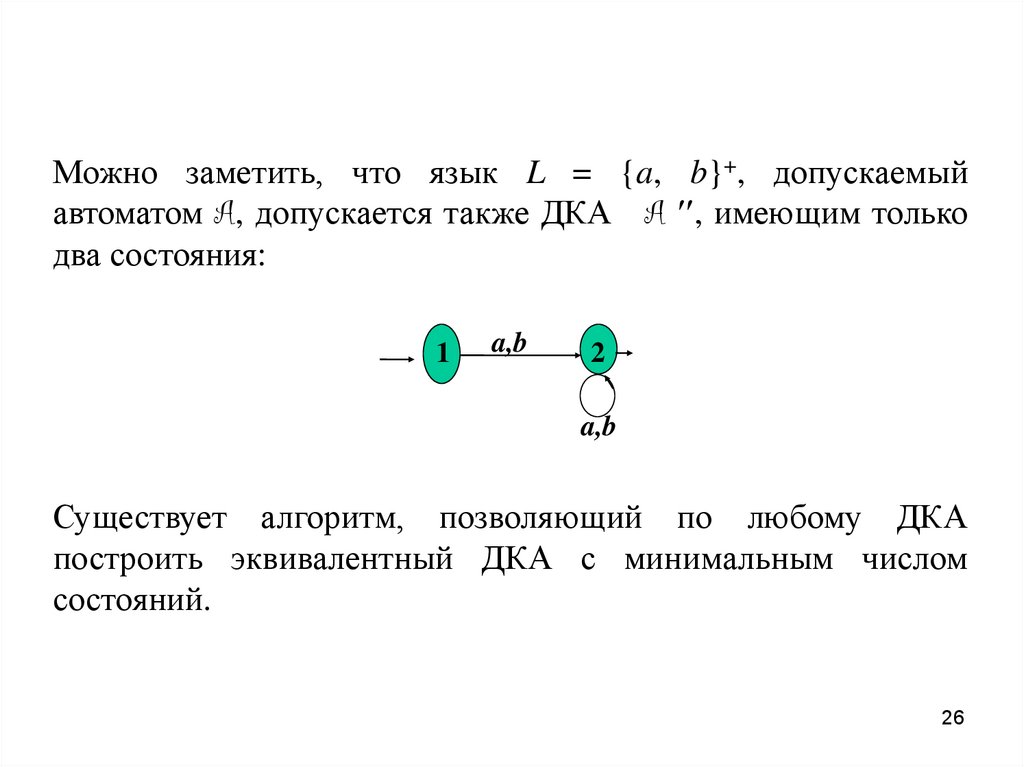
26.
Можно заметить, что язык L = {a, b}+, допускаемыйавтоматом A, допускается также ДКА A , имеющим только
два состояния:
1
a,b
2
a,b
Существует алгоритм, позволяющий по любому ДКА
построить эквивалентный ДКА с минимальным числом
состояний.
26
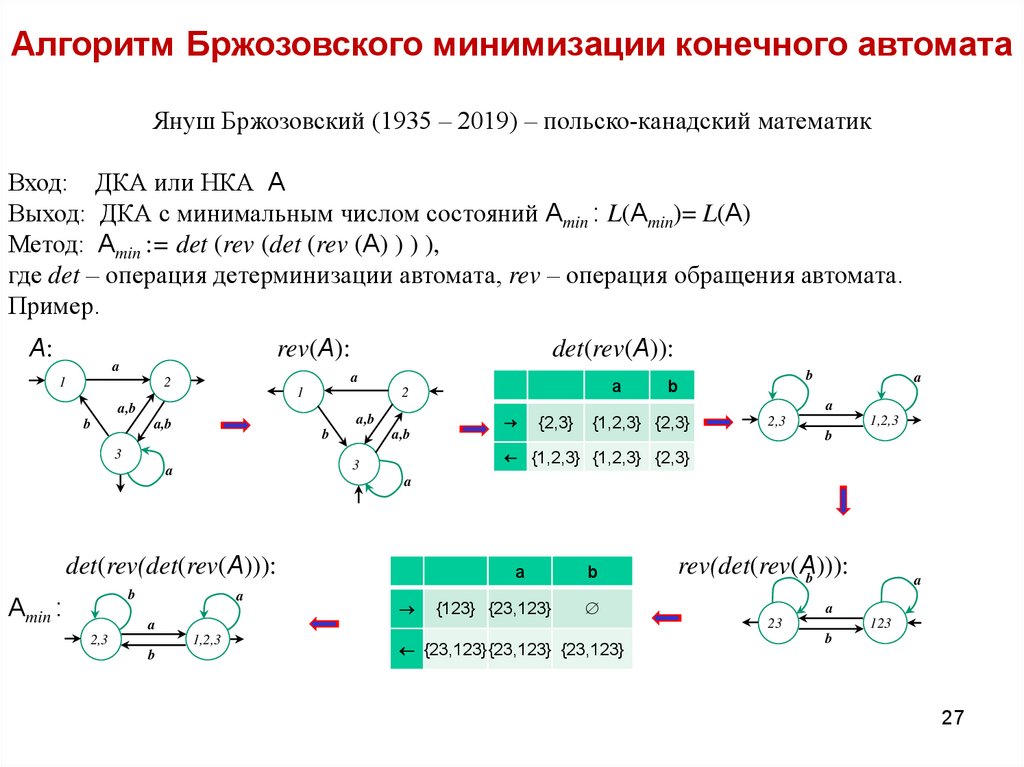
27. Алгоритм Бржозовского минимизации конечного автомата
Януш Бржозовский (1935 – 2019) – польско-канадский математикВход: ДКА или НКА A
Выход: ДКА с минимальным числом состояний Amin : L(Amin)= L(A)
Метод: Amin := det (rev (det (rev (A) ) ) ),
где det – операция детерминизации автомата, rev – операция обращения автомата.
Пример.
A:
rev(A):
a
1
a
2
1
b
b
a
a
a,b
a,b
b
3
a,b
3
a
{2,3}
{1,2,3} {2,3}
b
a
a
{123} {23,123}
b
rev(det(rev(A))):
b
{23,123}{23,123} {23,123}
a
a
123
23
1,2,3
b
b
{1,2,3} {1,2,3} {2,3}
a
2,3
1,2,3
2,3
a
det(rev(det(rev(A))):
Amin :
a
2
a,b
b
det(rev(A)):
b
27
28. Еще один пример детерминизации НКА
S B0 | 0B B0 | C1 | 0 | 1
C -> B0
НКА
ДКА
Праволин. гр-ка:
(H,0) = B
(H,0) = BS
H 0BS | 1B
(H,0) = S
(H,1) = B
B 0BCS
(H,1) = B
(B,0) = BCS
BS 0BCS
(B,0) = B
(BS,0) = BCS
BCS 0BCS | 1B
(B,0) = C
(BCS,0) = BCS
(B,0) = S
(BCS,1) = B
(C,1) = B
H – начальное состояние // начальный символ праволинейной
грамматики
BS и BCS – заключительные состояния (при построении леволинейной
грамматики сводятся в одно заключительное состояние - начальный
символ грамматики: S’ BS | BCS … )
28
29.
Лексический анализформальных языков
29
30. Задачи лексического анализа
1.выделить в исходном тексте цепочку символов, представляющую
лексему, и проверить правильность ее записи;
2.
удалить пробельные литеры и комментарии;
3.
преобразовать цепочку символов, представляющих лексему, в
пару:
( тип_лексемы,
4.
указатель_на_информацию_о_ней );
зафиксировать в специальных таблицах для хранения разных
типов лексем факт появления соответствующих лексем в
анализируемом тексте.
Чтобы решить эту задачу, опираясь на способ анализа с помощью
ДС, на дугах вводится дополнительные пометки-действия.
Теперь каждая дуга в ДС может выглядеть так:
A
t 1,t 2,...,t n
D 1;D 2;...;D m
B
30
31. Лексический анализ языков программирования
Принято выделять следующие типы лексем: идентификаторы,служебные слова, константы и ограничители.
Каждой лексеме сопоставляется пара:
( тип_лексемы,
указатель_на_информацию_о_ней ).
Таким образом, лексический анализатор - это транслятор, входом
которого служит цепочка символов, представляющих исходную
программу, а выходом - последовательность лексем.
Лексемы перечисленных выше типов можно описать с помощью
регулярных грамматик. Например,
идентификатор (I):
I → a | b| ...| z | Ia | Ib |...| Iz | I0 | I1 |...| I9
целое без знака (N):
N → 0 | 1 |...| 9 | N0 | N1 |...| N9
31
32. Описание модельного языка
P →program D1; B
D1 → var D { , D }
D → I { , I }: [ int | bool ]
B → begin S { ; S } end
S → I := E | if E then S else S | while E do S | B | read (I) | write (E)
E → E1 [ = | < | > | <= | >= | != ] E1 | E1
E1 → T { [ + | - | or ] T }
T →
F { [ * | / | and ] F }
F →
I | N | L | not F | (E)
L →
I →
N→
true | false
a | b| ...| z | Ia | Ib |...| Iz | I0 | I1 |...| I9
0 | 1 |...| 9 | N0 | N1 |...| N9
Замечания:
запись вида { } означает итерацию цепочки , т.е. в порождаемой
цепочке в этом месте может находиться либо , либо , либо ,
либо и т.д.
32
запись вида [ | ] означает, что в порождаемой цепочке в этом
33. Контекстные условия
Любое имя, используемое в программе, должно быть описано и толькоодин раз.
В операторе присваивания типы переменной и выражения должны
совпадать.
В условном операторе и в операторе цикла в качестве условия возможно
только логическое выражение.
Операнды операции отношения должны быть целочисленными.
Тип выражения и совместимость типов операндов в выражении
определяются по обычным правилам; старшинство операций задано
синтаксисом.
В любом месте программы, кроме идентификаторов, служебных слов и
чисел, может находиться произвольное число пробелов и
комментариев вида { < любые символы, кроме ‘}’ , ‘{‘ и ‘ ’ > }.
Program, var, int, bool, begin, end, if, then, else, while, do, true, false, read
и write - служебные слова (их нельзя переопределять).
Используется паскалевское правило о разделителях между
идентификаторами, числами и служебными словами.
33
34. Представление лексем
Тип лексемы - задается следующим перечислимым типом:enum type_of_lex {
LEX_NULL, /*0*/
LEX_AND, LEX_BEGIN, … LEX_WRITE, /*18*/
LEX_FIN, /*19*/
LEX_SEMICOLON, LEX_COMMA, … LEX_GEQ, /*35*/
LEX_NUM, /*36*/
LEX_ID, /*37*/
POLIZ_LABEL, /*38*/
POLIZ_ADDRESS, /*39*/
POLIZ_GO, /*40*/
POLIZ_FGO }; /*41*/
Значение лексемы - это номер строки в таблице лексем
соответствующего класса, содержащей информацию о лексеме,34
или непосредственное значение, в случае целых чисел.
35. Таблицы, используемые в лексическом анализаторе модельного языка
TW - таблица служебных слов М-языка;TD - таблица разделителей (ограничителей) М-языка;
TID - таблица идентификаторов анализируемой программы.
35
36.
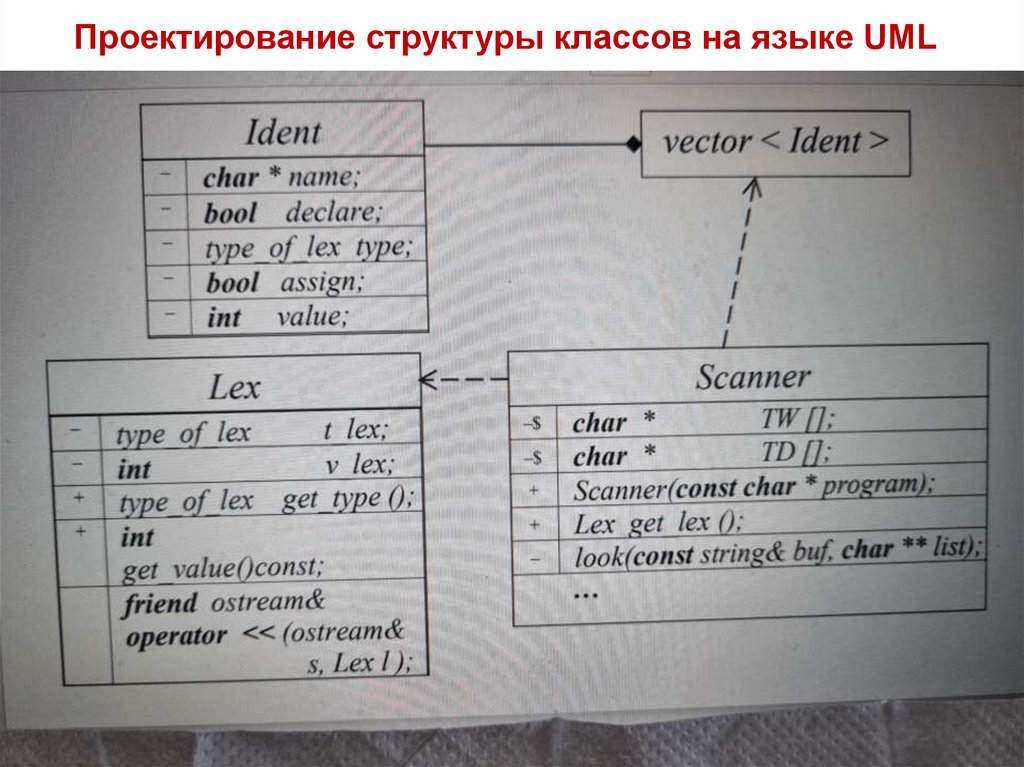
Проектирование структуры классов на языке UML36
37. Класс Lex
class Lex {type_of_lex t_lex;
int v_lex;
public:
Lex ( type_of_lex t = LEX_NULL, int v = 0) {
t_lex = t;
v_lex = v;
}
type_of_lex get_type ( ) const {
return t_lex;
}
int get_value ( ) const {
return v_lex;
}
friend ostream& operator << (ostream & s, Lex l ) {
s << '(' << l.t_lex << ',' << l.v_lex << ");" ;
return s;
37
38. Класс Ident
class Ident { string name;bool declare;
type_of_lex type;
bool assign;
int value;
public:
Ident ( ) { declare = false; assign = false; }
Ident ( const char * n ) {
name = n; declare = false; assign = false; }
bool operator== (const string& s) const { return name == s; }
char * get_name ( ) const { return name; }
bool get_declare ( ) const { return declare; }
void put_declare ( ) { declare = true; }
type_of_lex get_type ( ) const { return type; }
void put_type ( type_of_lex t ) { type = t; }
bool get_assign ( ) const { return assign; }
void put_assign ( ) { assign = true; }
38
int get_value ( ) const { return value; }
39. Таблица идентификаторов TID
vector <Ident> TID;int put (const string & buf) {
vector <Ident> :: iterator k;
if ( (k = find (TID.begin(), TID.end(), buf)) != TID.end() ) )
return k – TID.begin();
TID.push_back ( Ident (buf) );
return TID.size() - 1;
}
39
40. Класс Scanner
class Scanner {FILE *fp;
char c;
int look (const string& buf, char * * list) {
int i = 0;
while (list [ i ]) {
if ( buf == list [ i ] )
return i;
i++; }
return 0; }
void gc ( ) { c = fgetc ( fp ); }
public:
static const char * TW [ ], * TD [ ];
Scanner (const char * program) {
fp = fopen ( program, "r" );
}
Lex get_lex ();
40
41. Таблицы лексем для М-языка
const char * Scanner:: TW [ ] ={ NULL,"and","begin","bool","do","else","end",
//
1
2
3
4
5
6
"if","false","int","not","or","program","read",
// 7
8
9
10
11
12
13
"then","true","var","while","write“ };
// 14
15
16
17
18
const char * Scanner:: TD [ ] = {NULL, ";", "@", ",", ":", ":=",
//
1
2
3
4
5
"(", ")", "=","<", ">", "+", "-", "*", "/", "<=", ">="};
//
6 7 8 9 10 11 12 13 14 15
16
41
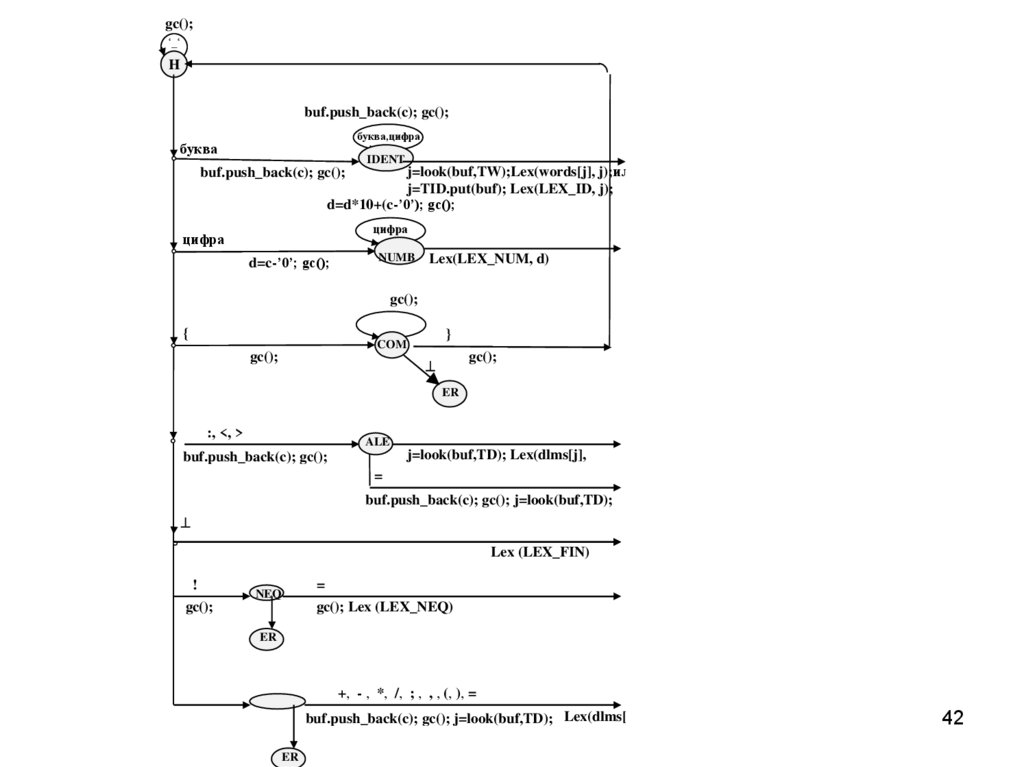
42.
gc();‘ ‘
H
buf.push_back(c); gc();
буква,цифра
буква
IDENT
j=look(buf,TW);Lex(words[j], j);или
j=TID.put(buf); Lex(LEX_ID, j);
d=d*10+(c-’0’); gc();
buf.push_back(c); gc();
цифра
цифра
d=c-’0’; gc();
NUMB
Lex(LEX_NUM, d)
gc();
{
}
COM
gc();
gc();
ER
:, <, >
ALE
buf.push_back(c); gc();
=
j=look(buf,TD); Lex(dlms[j],
j)
buf.push_back(c); gc(); j=look(buf,TD);
Lex(dlms[j], j);
lex(2,N:=)
!
gc();
Lex (LEX_FIN)
=
gc(); Lex (LEX_NEQ)
NEQ
ER
+, - , *, /, ; , , , (, ), =
buf.push_back(c); gc(); j=look(buf,TD); Lex(dlms[j], j);
ER
42
43.
Lex Scanner::get_lex ( ) { enum state { H, IDENT, NUMB, COM, ALE, NEQ };state CS = H; string buf; int d, j;
do { gc (); switch(CS) {
case H: if ( c == ' ' || c == '\n' || c == '\r' || c == '\t‘ )
else
if ( isalpha(c)) { buf.push_back(c); CS = IDENT; }
else
if ( isdigit (c) ) { d = c - '0'; CS = NUMB; }
else
if ( c == '{' ) { CS = COM; }
else
if ( c == ':' || c == '<' || c == '>') {
buf.push_back(c); CS = ALE; }
else
if ( c == '@') return Lex (LEX_FIN);
else
if ( c == '!‘ ) buf.push_back(c); CS = NEQ;
else { buf.push_back(c);
if ( (j = look ( buf, TD)) )
43
return Lex ( (type_of_lex) (j + (int) LEX_FIN), j );
44.
case IDENT:if ( isalpha(c) || isdigit(c) ) {
buf.push_back(c); }
else { ungetc(c, fp);
if ( j = look (buf, TW) )
return Lex ((type_of_lex) j , j );
else {
j = put (buf);
return Lex (LEX_ID, j);
}
break;
case NUMB:
if ( isdigit (c) ) {
d = d * 10 + (c - '0'); }
else { ungetc(c, fp);
return Lex ( LEX_NUM, d); }
break;
case COM:
if ( c == '}' ) { CS = H; }
else
44
45.
case ALE:if ( c == '=‘ ) {
buf.push_back(c);
j = look ( buf, TD );
return Lex ((type_of_lex) ( j + (int) LEX_FIN), j );
}
else {
ungetc(c, fp);
j = look (buf, TD);
return Lex ((type_of_lex) ( j + (int) LEX_FIN), j ); }
break;
case NEQ:
if ( c == '=‘ ) {
buf.push_back(c); j = look ( buf, TD );
return Lex ( LEX_NEQ, j ); }
else throw '!';
break;
} //end switch
} while ( true );
45






































 programming
programming