Similar presentations:
Бинарные отношения
1.
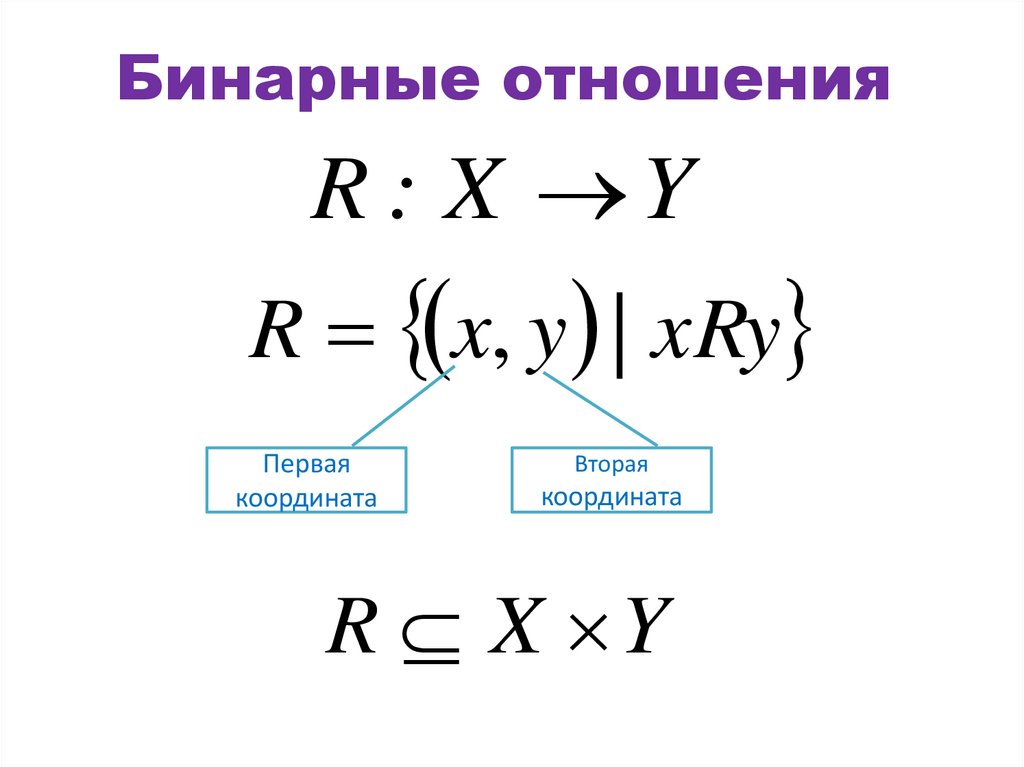
Бинарные отношенияR : X Y
R x, y | xRy
Первая
координата
Вторая
координата
R X Y
2.
Способы задания бинарныхотношений
X 2,3,4,5,6
Y 2,3,4
1) перечисление пар:
R 2,2 , 3,3 , 4,2 , 4,4 , 6,2 , 6,3
2) указание характеристического свойства:
- х делится на у
2 3 4 5 6
3) матричный:
2 1 0 1 0 1
MR
3 0 1 0 0 1
4 0 0 1 0 0
3.
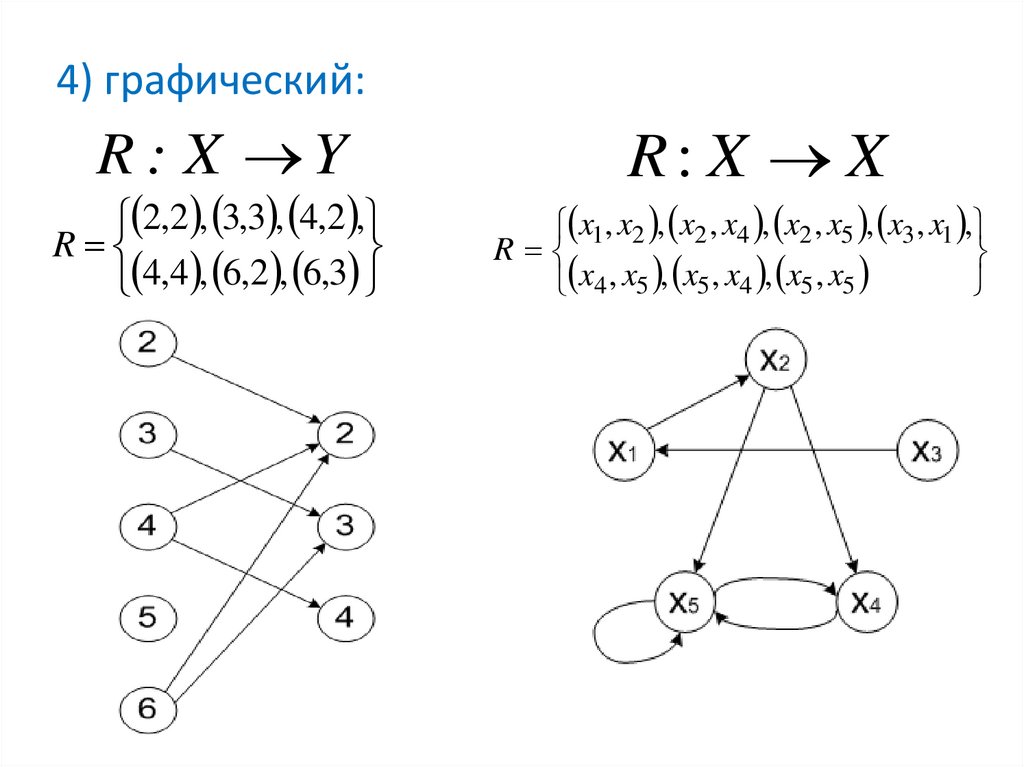
4) графический:R : X Y
2,2 , 3,3 , 4,2 ,
R
4,4 , 6,2 , 6,3
R: X X
x1, x2 , x2 , x4 , x2 , x5 , x3 , x1 ,
R
x4 , x5 , x5 , x4 , x5 , x5
4.
Область определения: Dom R XDom R x | y Y : xRy
Область значений: Im R Y
Im R y | x X : xRy
Dom R x1 , x3 , x4 , x5
Im R y1 , y2 , y4
5.
Сечения: R( xi ) y | xi RyX {x1 , x2 , x3};
Y { y1, y2 , y3 , y4 }
R {( x1, y1 ), ( x1 , y3 ), ( x2 , y1 ), ( x2 , y3 ),
( x2 , y4 ), ( x3 , y1 ), ( x3 , y2 ), ( x3 , y4 )}
R( x1 ) { y1, y3}, R( x2 ) { y1, y3 , y4}, R( x3 ) { y1, y2 , y4}.
Фактор-множество: Y R R( xi ) : xi X
x2
x3
x1
{ y , y } { y , y , y } { y , y , y }
1 3 4
1 2 4
1 3
6.
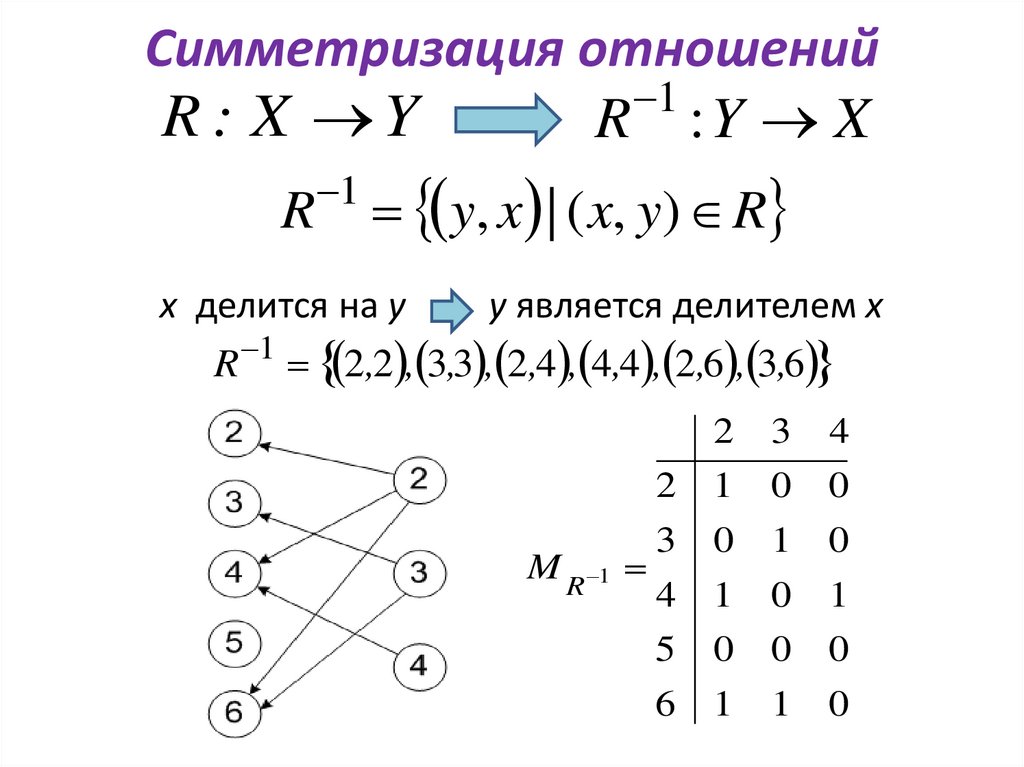
Симметризация отношений1
R : X Y
R :Y X
R
1
y, x | ( x, y) R
х делится на у
у является делителем х
R 1 2,2 , 3,3 , 2,4 , 4,4 , 2,6 , 3,6
2
3
M R 1
4
5
6
2
1
0
1
0
1
3
0
1
0
0
1
4
0
0
1
0
0
7.
Композиция отношенийА: X Y, B :Y Z
С А В : Х Z
C x, z | y : ( x, y) A ( y, z) B
A x1 , y2 , x1 , y3 , x2 , y3 , x4 , y1 , x4 , y2
B y1 , z3 , y1z4 , y2 , z5 , y3 , z2
x1, z2 , x1, z5 , x2 , z2 ,
C A B
x4 , z3 , x4 , z4 , x4 , z5
MC M B M A
8.
Свойства бинарных отношенийR: X X
- Рефлексивность
Е R
x : xRx
- Антирефлексивность
- Симметричность
x, y : yRx xRy
- Асимметричность
R R 1
- Антисимметричность
xRy
x, y :
x y
yRx
R R 1 E
x : xRx
Е R=
xRy yR x
R R 1
- Транзитивность
xRy
x, y, z :
xRz
yRz
R R R





 informatics
informatics








