Синтез цифровых фильтров методом взвешивания с помощью оконных функций

1.

Кафедра электроники и
микропроцессорной техники
Расчетно-графическая работа по дисциплине
«Цифровая обработка сигналов»
Синтез цифровых фильтров
методом взвешивания с помощью
оконных функций

2.

Синтез ЦФ методом взвешивания с помощью оконных
функций
1. Задать в интервале w→[0, p/T] периодическую функцию дискретной амплитудной
частотной характеристики (АЧХ) ФНЧ вектором – A(w);
2. Подставить A(w) в формулу обратного дискретного преобразования Фурье
(ОДПФ) для получения коэффициентов h(m) – импульсной характеристики (ИХ);
3. Сдвинуть во временной области ИХ на m интервалов;
4. Подставить h(m) в формулу дискретного преобразования Фурье (ДПФ) для
получения АЧХ;
5. Получить усечённую и сглаженную оконным преобразованием h’(m) ИХ;
6. Подставить h’(m) в формулу ДПФ для получения сглаженной АЧХ;
7. Оценить групповое время задержки как взятая с обратным знаком производная
ФЧХ по частоте;
8. Построить блок-схему КИХ фильтра;
9. Оценка параметров и характеристик ФНЧ средствами MatLab;
10. Трансформации ФНЧ в ФВЧ.

3.

Сущность метода взвешивания с помощью оконных функций
заключается в получении ИХ конечной длинны путем усечения
ИХ бесконечной длинны
1. Задать в интервале w→[0, p/T] периодическую функцию
дискретной амплитудной частотной характеристики (АЧХ) ФНЧ
вектором – A(w)
wc 30000
w 0
A ( w)
T 0.00003
N 21
fc
p
wc
fs
2 p
3
T
fc 4.775 10
1 if 0 w wc
0 if wc w
i 1
T
4
fs 3.333 10
1
p
T
1
A( w )
0.5
0
4
5 10
w
1 10
5

4.

2. Подставить A(w) в формулу обратного дискретного
преобразования Фурье (ОДПФ) для получения коэффициентов
h(m) – импульсной характеристики (ИХ)
N 1
1
h( m ) F H ( jω ) A( ω ) e jmωT
N m 0
1
H A ( w)
w
m 0
N 1
hh
w
2
1
N
N 1
m 0
H e
w
hh
i m w T
h
m
1
hm
0.5
0
2
4
6
m
8
10
m
1

5.

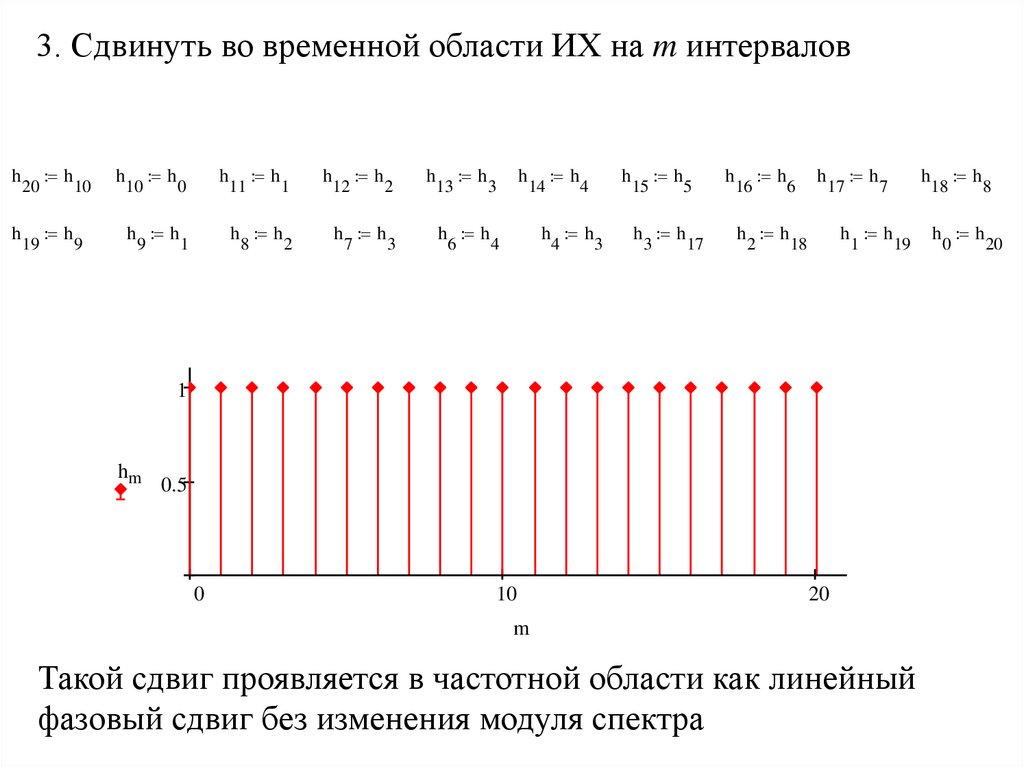
3. Сдвинуть во временной области ИХ на m интервалов
h
h
20
19
h
h
10
9
h
10
h
h h
9
h
0
11
h
1
h h
1
8
2
h
12
h
2
h h
7
3
h
13
h
h h
6
h
3
14
h
h h
4
4
h
4
3
15
h
5
h h
3
17
h
16
h
6
h h
2
h
17
h
h h
18
1
h
7
19
1
hm
0.5
0
10
20
m
Такой сдвиг проявляется в частотной области как линейный
фазовый сдвиг без изменения модуля спектра
18
h
8
h h
0
20

6.

4. Подставить h(m) в формулу дискретного преобразования Фурье
(ДПФ) для получения АЧХ
N 1
W ( ω ) F h( m ) hm e jmωT
m 0
20
N 1
Ww 10
W
w
m 0
4
5
5 10
0
1 10
w
K 20 log W
w
h e i m w T
m
50
w
0
Kw
50
100
0
4
5 10
w
5
1 10

7.

5. Получить усечённую и сглаженную оконным
преобразованием h’(m) ИХ
h ( m ) h( m ) w( m )
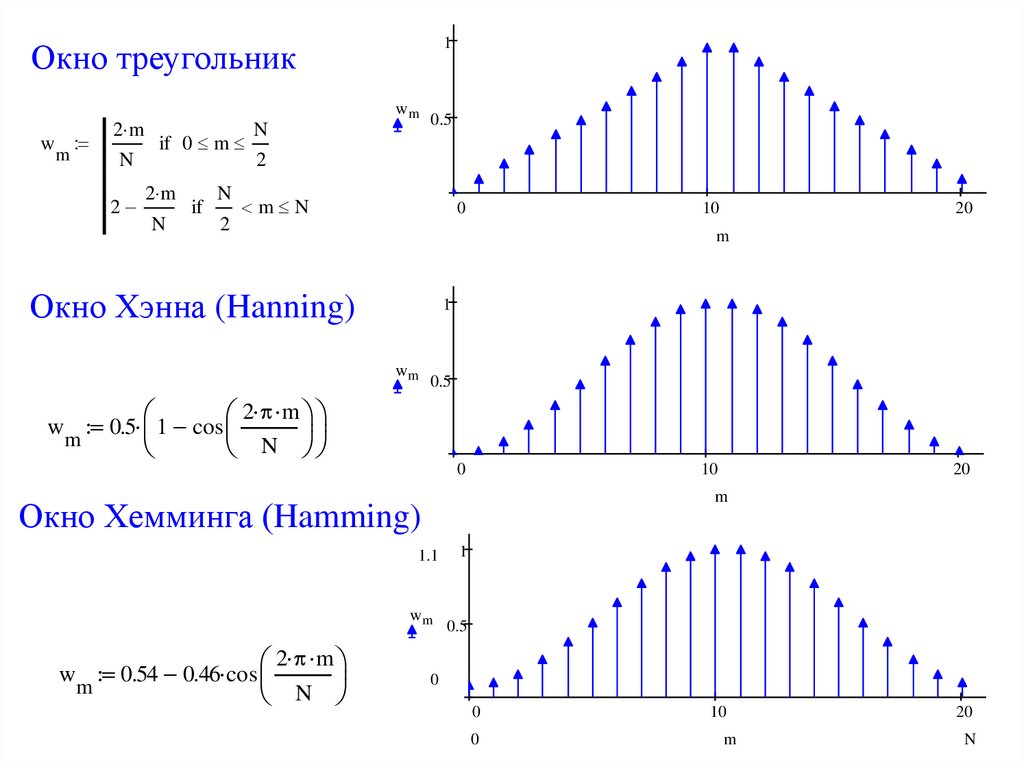
Окно Блэкмана
w 0.42 0.5 cos
1
wm
2 p m
0.08 cos
N
m
4 p m
N
0.5
0
10
20
m
hw h w
m
m
1
m
hwm
0.5
0
10
m
20

8.

1
Окно треугольник
w
m
wm
2 m
if 0 m
N
2
2 m
N
if
N
2
N
0.5
2
m N
0
1
wm
m
0.5
2 p m
N
0
10
w 0.54 0.46 cos
2 p m
N
20
m
Окно Хемминга (Hamming)
m
20
m
Окно Хэнна (Hanning)
w 0.5 1 cos
10
1.1
1
wm
0.5
0
0
10
20
0
m
N

9.

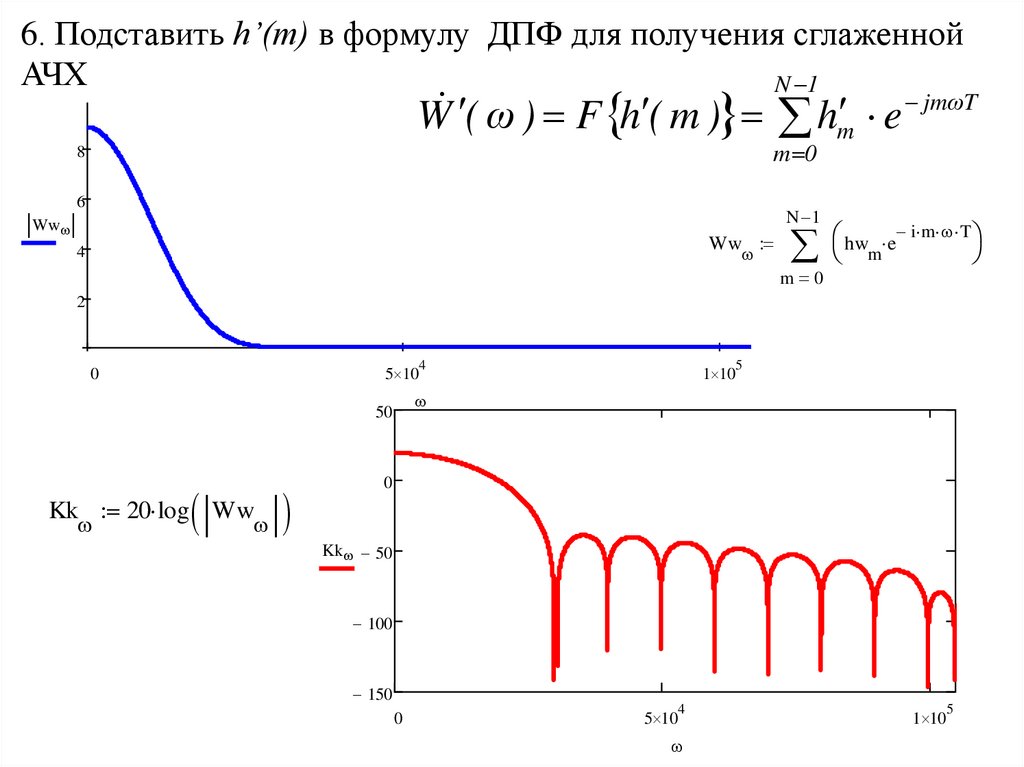
6. Подставить h’(m) в формулу ДПФ для получения сглаженной
АЧХ
N 1
W ( ω ) F h ( m ) hm e jmωT
m 0
8
6
N 1
Www
Ww
w
4
m 0
hw e i m w T
m
2
5 10
0
w
w
5
1 10
w
50
Kk 20 log Ww
4
0
Kkw 50
100
150
0
4
5 10
w
5
1 10

10.

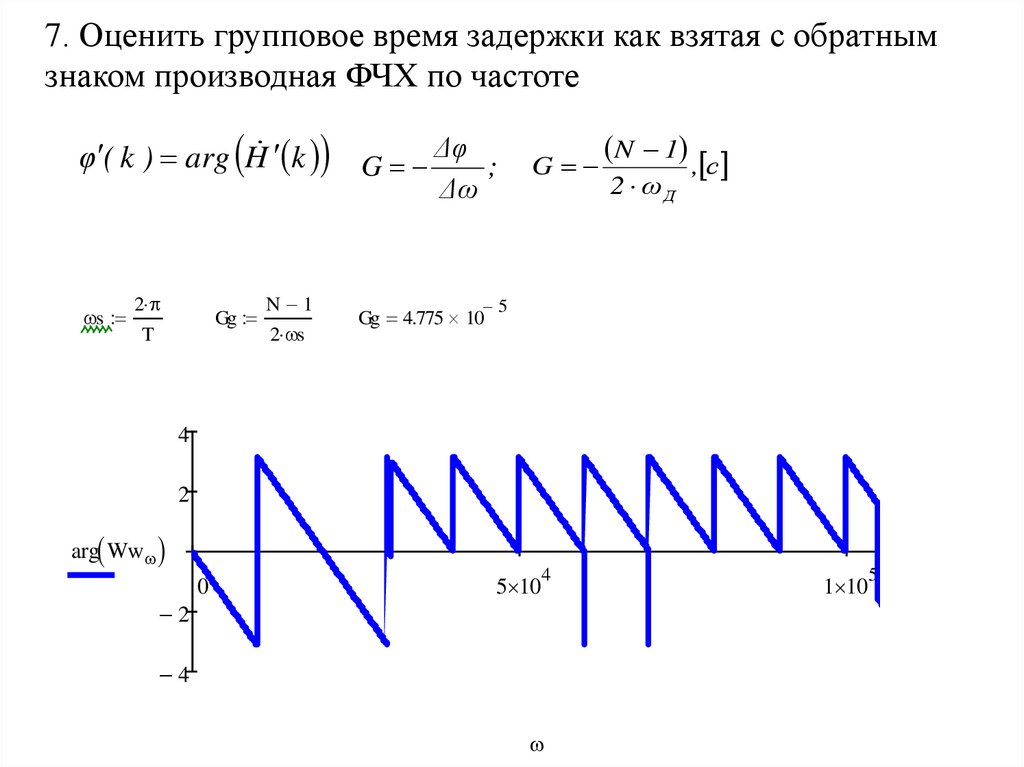
7. Оценить групповое время задержки как взятая с обратным
знаком производная ФЧХ по частоте
φ ( k ) arg H k G Δφ ;
Δω
ws
2 p
Gg
T
N 1
2 ws
G
N 1 , с
2 ωД
5
Gg 4.775 10
4
2
arg Www
0
5 10
4
2
4
w
1 10
5

11.

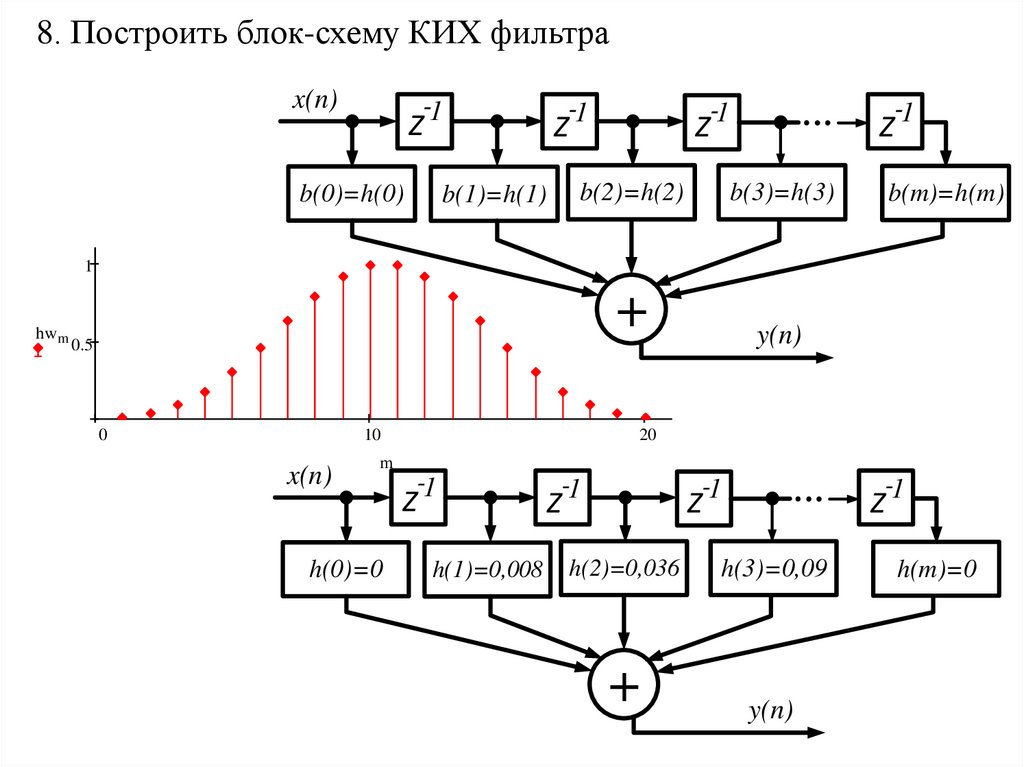
8. Построить блок-схему КИХ фильтра
x(n)
-1
b(0)=h(0)
b(1)=h(1)
-1
-1
-1
b(2)=h(2)
b(3)=h(3)
+
y(n)
b(m)=h(m)
1
hwm
0.5
0
10
x(n)
m
h(0)=0
20
-1
-1
h(1)=0,008
h(2)=0,036
h(3)=0,09
+
y(n)
-1
-1
h(m)=0

12.

9. Оценка параметров и характеристик ФНЧ средствами MatLab

13.

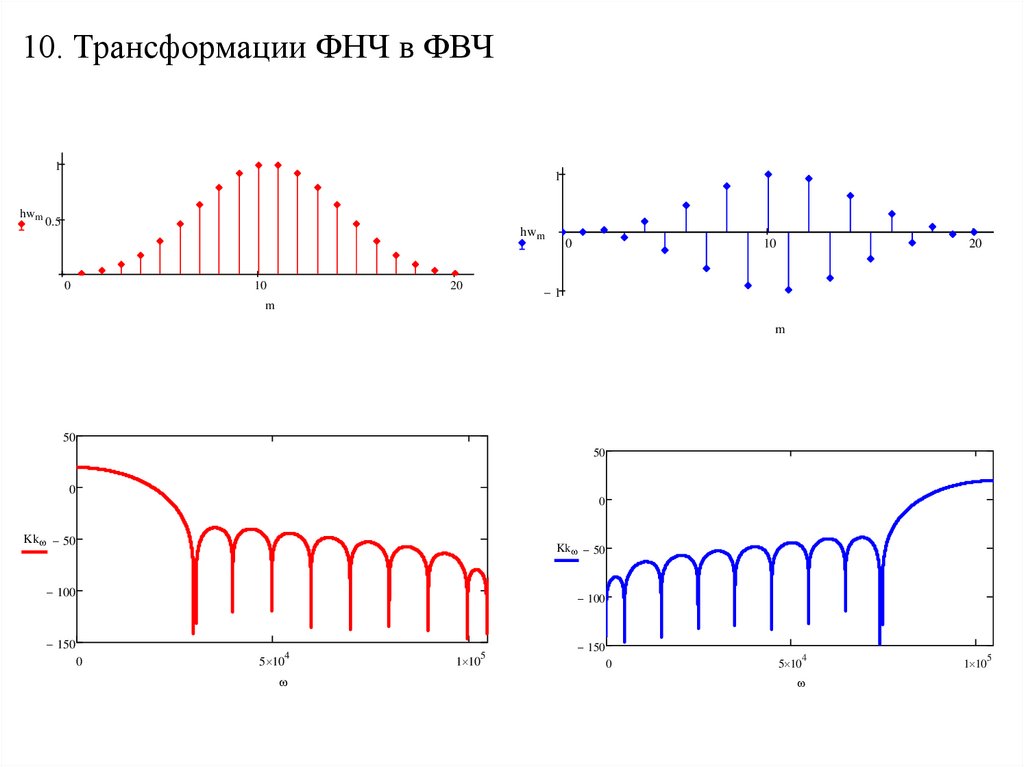
10. Трансформации ФНЧ в ФВЧ
1
hwm
1
0.5
hwm
0
10
20
0
10
20
1
m
m
50
50
0
0
Kkw 50
Kkw 50
100
100
150
0
4
5 10
w
5
1 10
150
0
4
5 10
w
5
1 10