Mncgehhoe pemehhe osparaoh 3agahh gga ypabhehha

1.

MOCKOBCKHH rOCyflAPCTBEHHblH YHHBEPCHTET HMEHH M. B. gOMOHOCOBA OAKYHbTET
BHHHC^HTE^bHOH MATEMATHKH U KHBEPHETHKH KAOEflPA MATEMATHHECKOH OH3HKH
BOHKAPEB CEMEH B^AflHC^ABOBHH
MncgeHHoe pemeHHe oSparaoH 3agaHH gga ypaBHeHHA
Ten^onpoBogHOCTH c Ma^HM napaMeTpoM npu CTapmefi
npOH3BOgHOH
nPEggwngoMHAg nPAKTHKA
Hay^HMH pyKOBogHTe^b:
g.o-M.H., npooECCOP A. M.
gEHHCOB
MoCKB
a
2022

2.

Cogep^aHHe
2
OSpaTHaa 3agaaa 1
Bamog ^opMy,nH gna O3 1 3
PacaeTai gna O3 1 4
HcxogHMe gaHHae c norpemHOCTbro gna O31 9
OSpaTHaa 3agaaa 2 10
Bamog ^opMyna gna O3 2
PacaeTM gna O3 2
11
12
HcxogHaie gaHHae c norpemHocTbro gna O32 14
OSpaTHaa 3agaaa 3 15
Bamog ^opMyna gna O3 3
PacaeTM gna O3 3
16
18
CnacoK ^THpyeMoft nHTepaTypai 26
1

3.

06paTHaa 3agana 1
PaccMOTpuM Ha^a^bHO-KpaeByro 3aga^y g^a ypaBHeHua Ten.nonpoBogHOCTH c CHHrynapHMM BO3Mym,eHHeM
u t ( x , t ) = £2 u x x ( x , t ) , ( x , t ) E Q T , (1)
«x(0,t) = Ux(n,t) = 0, 0 < t < T, (2) u(x, 0) = <^(x), 0 < x < n. (3)
nycTb ^yHKgua <^(x) Heu3BecTHa. TpeSyeTca onpege^HTb <^(x), ec^H 3agaHa gono^HHTe^BHaa HH^opMa^a o pemeHHH 3aga^H (1)-(3)
u(x,T) = g ( x ) ,
2
0 < x < n.

4.

Bbreog ^opMy^M gna 03 1
PaccMOTpuM HaaaabHo-KpaeByro 3agaay gaa ypaBHeHua TenaonpoBogHocTu c CUH-ryaapHbiM Bo3Mym,eHueM
ut(x,t) = e2 u xx (x, t ) , (x,t) e Q T , (1) ux(0,t) = ux(n,t) = 0, 0 < t < T, (2) u(x, 0) = <^(x), 0 < x
< n. (3)
e - noflo*HTejbHHH Ma^un napaMeTp. PemeHue ^TOH 3agaau 6ygeM o6o3HaaaTb u(x, t; e).
npegno^o^HM, aTo ^yHKnua <^(x) ygoBaeTBopaeT caegyromuM ycaoBuaM:
p e C2m+4[0,n], ^(2k+1)(0) = <^(2k+1)(n) = 0, k = 0,1,...,m + 1. (4)
Xopomo H3BecTHo, aTo pemeHue 3agaau (1)-(3) uMeeT Bug
1 nn °°^ pn
u(x,t; e) = — <^(s) ds +
n J 0
— <p(s) cos ns ds exp(- e2n2t) cos nx. (5)
n=1
n J
0
npuMeHUB ^opMyny Teaaopa u ucnoab3oBaB ycaoBua (4), noayauM, aTo gaa ^yHK-guu
u(x,t; e) cnpaBegauBo npegcTaBaeHue
m
tk t
2k
u(x,t; e) = <p(x) + ^2 e —^(2k)(x) + e2(m+1)vm+i(x, t; e). (6
k=1
C^opMyaupyeM o6parayro 3agaay. nycTb ^yHKnua <^(x) Heu3BecTHa. Tpe6yeTca
onpegeauTb <^(x), ecau 3agaHa gonoaHuTeabHaa uH^opMagua o pemeHuu 3agaau
(1)-(3):
u(x,T ; e) = g(x; e), 0 < x < n.(7)
nycTb m =1. YauTbrnaa pa3ao*eHue (6), onpegeauM npu6au*eHHoe pemeHue o6paTHoa 3agaau
KaK pemeHue KpaeBoa 3agaau
e2T^"(x; e) + <^(x; e) = g(x; e), 0 < x < n,
^/(0;e) = ^/(n;e) = °.
PemeHue ^TOH 3agaau onpegeaaeTca ^opMyaoa
x
<^(x; e) = e-1T-1/2[sin(e-1T-1/2n)]-1(cos[e-1T-1/2(x-n)W cos(e-1T-1/2s)g(s; e) ds+
J0
rn
cos(e-1T-1/2x) / cos[e-1T-1/2(s — n)]g(s; e) ds)
3

5.

PacneTM gna 03 1
npu6au:xeHHoe pemeHue 3agaau onpegeaaeTca ^opMyaoii
pX
<p(x; e) = £-1T-1/2[sin(e-1T-1/2n)]-1(cos[e-1T-1/2(x—n)] cos(e-1T-1/2s)g(s; e) ds+
J0
pn
cos(e-1T-1/2x) cos[e-1T-1/2(s — n)]g(s; e) ds)
X
gaa noayaeHua pacaeToB nporpaMMHO peaau3yeM onncaHHHH MeTog. gaa ^TO^o
BBegeM ceTKy c maroM h = —, rge n - aucao KopHea nogbiHTerpaabHoa foyHKauu
n
Ha oTpe3Ke [0,n] + 2 u goMHo:xeHHoe Ha 5.
nocauTaeM 3HaaeHue ^yHKguu B Ka^goM y3ae ceTKu. gaa ^TO^o B ^opMyay BMecTo x
nogcTaBHM Hamu gucKpeTHbie 3HaaeHua. gaabme no MeTogy Tpanegua cauTaeM uHTerpaabi,
ucnoab3ya Ty *e ceTKy.
npoTecTpuyeM nporpaMMy. Bo3bMeM <^(x) = 2cos(2x) + 3cos(3x), Torga g(x) = 2e-4T^ cos(2x) +
3e-9T^ cos(3x).
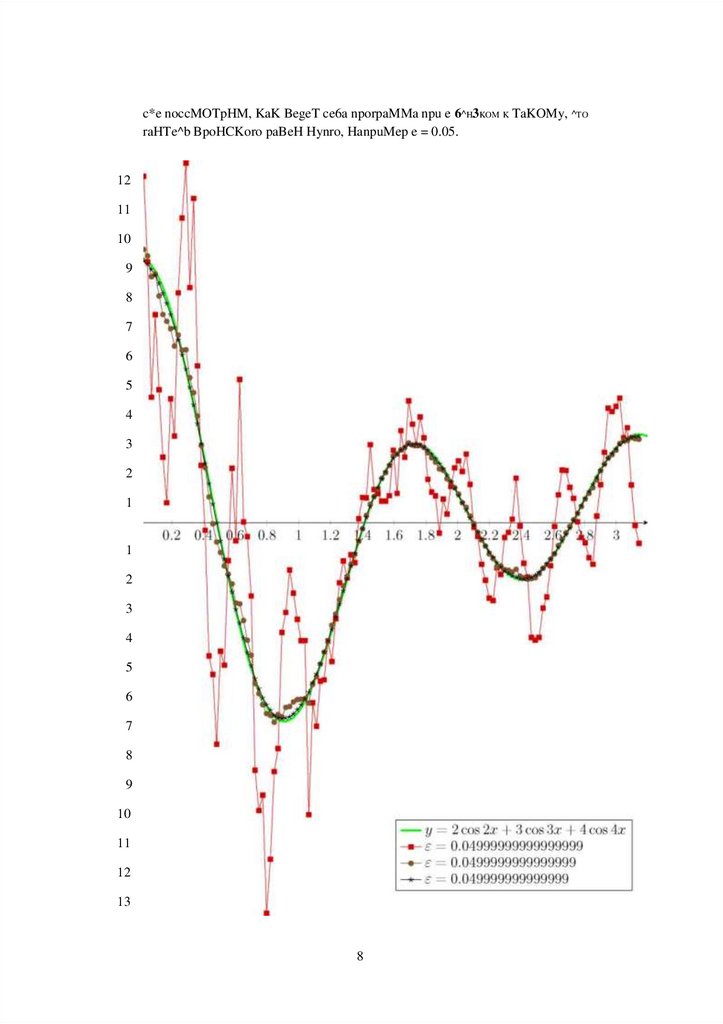
nocTpouM rpa^HK c TOHHMM pemeHueM odparaon 3agaau u npu6au:xeHHbiMu pe-meHHaMH
gaa pa3Hbix e u gaa T = 1. no HeMy MOXHO cgeaaTb Bbmog, aTo gaa MeHbmero e
npu6au:xeHHoe pemeHue ayame, a gaa Soabmero e npudau^eHHoe pe-meHue cuabHo oTauaaeTca
OT ToaHoro.
4

6.

7.

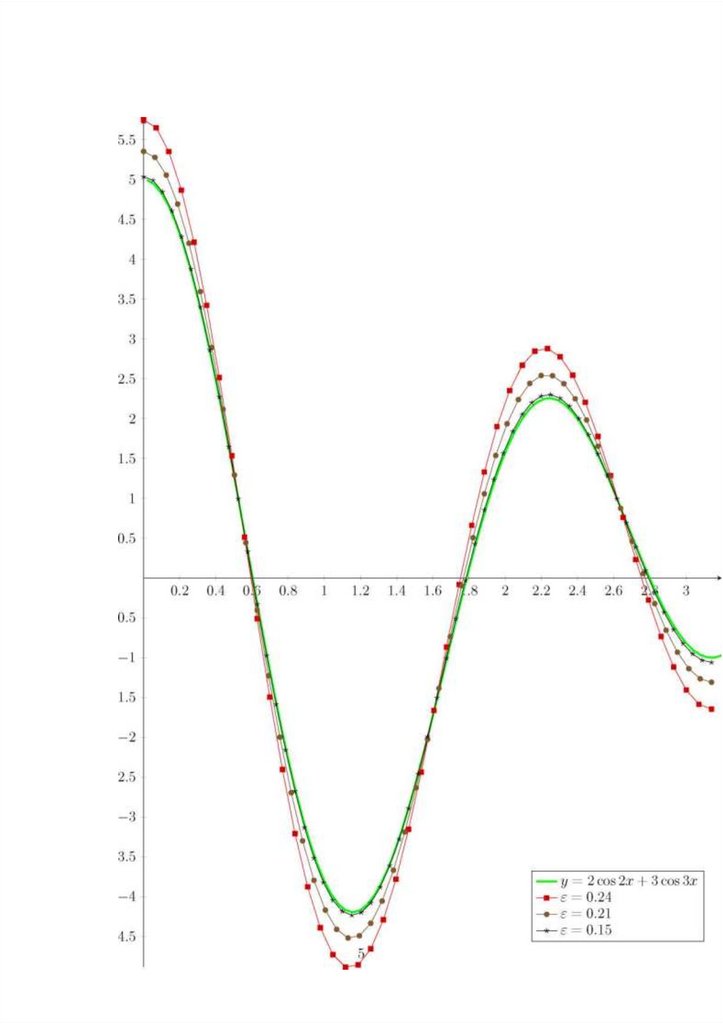
K*e noccMOTpuM, KaK BegeT ce6a nporpaMMa npu e 6^H3KOM K TaKOMy, ^TO
H^HTe^b BpoHCKoro paBeH Hynro, HanpuMep e = 0.1.
6
5
4
3
2
1
1
2
3
4
5
6
7
8
6

8.

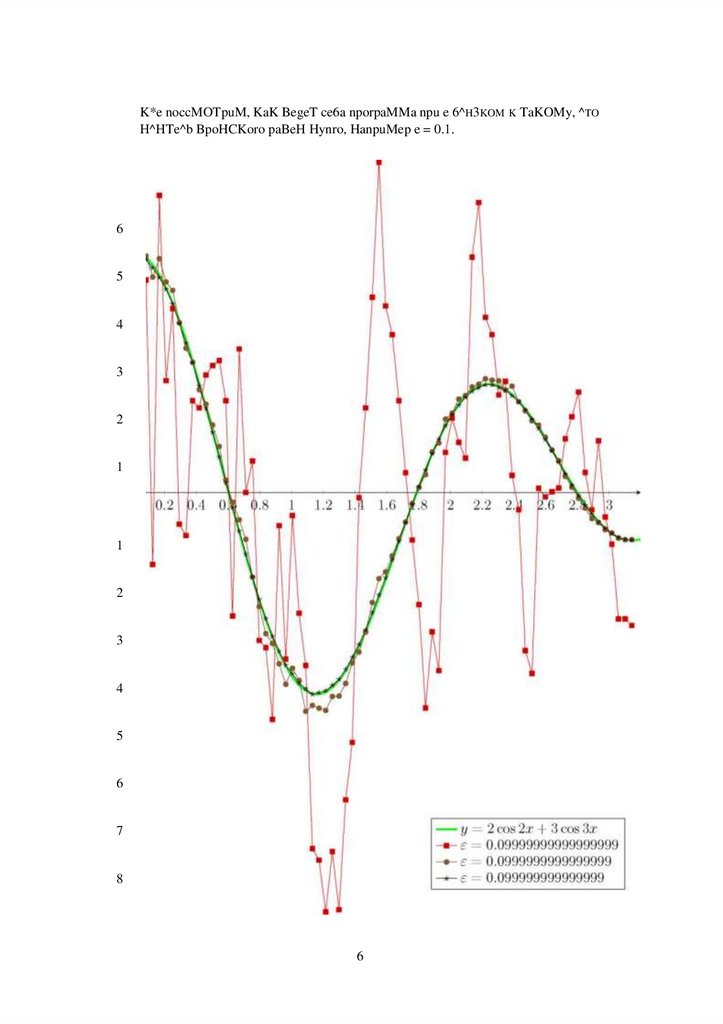
3 neptB03bMeM i p ( x ) = 2 cos(2x)+3 cos(3x)+4 cos(4x), Torga g ( x ) = 2 e
cos(2x) + ^ cos(3x) + 4e-16T^ cos(4x).
4T^
9
8
7
6
5
4
3
2
1
1
2
3
4
5
y = 2 cos 2x + 3 cos 3x + 4 cos 4x e
= 0.19 e = 0.15 e = 0.06
6
7
8
7

9.

c*e noccMOTpHM, KaK BegeT ce6a nporpaMMa npu e 6^H3KOM K TaKOMy, ^TO
raHTe^b BpoHCKoro paBeH Hynro, HanpuMep e = 0.05.
12
11
10
9
8
7
6
5
4
3
2
1
1
2
3
4
5
6
7
8
9
10
11
12
13
8

10.

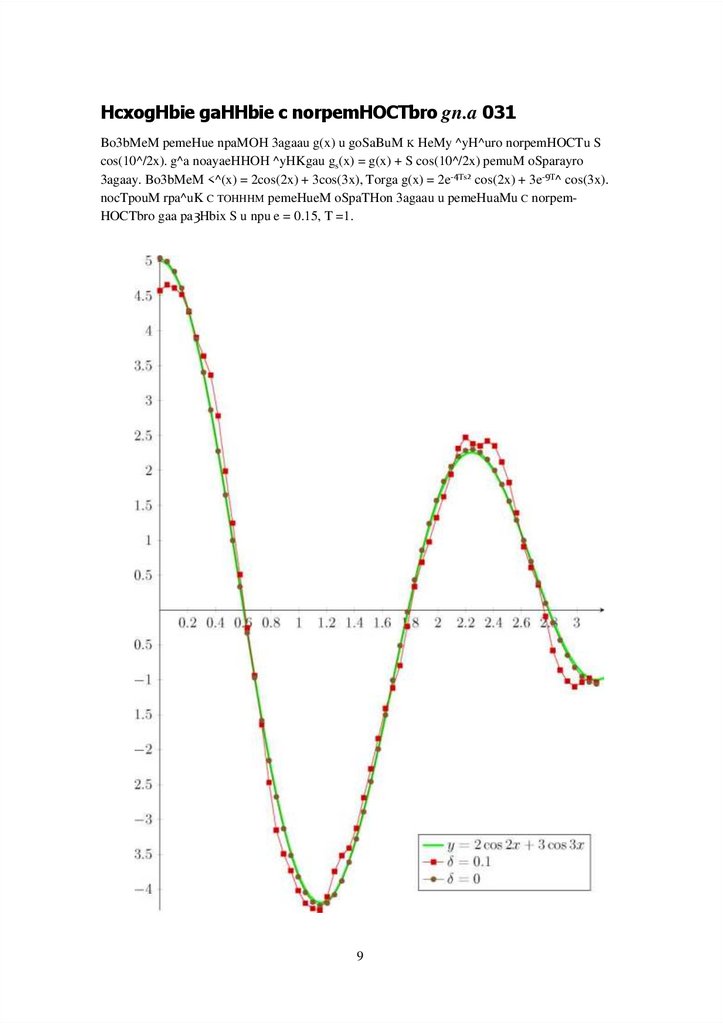
HcxogHbie gaHHbie c norpemHOCTbro gn.a 031
Bo3bMeM pemeHue npaMOH 3agaau g(x) u goSaBuM K HeMy ^yH^uro norpemHOCTu S
cos(10^/2x). g^a noayaeHHOH ^yHKgau gs(x) = g(x) + S cos(10^/2x) pemuM oSparayro
3agaay. Bo3bMeM <^(x) = 2cos(2x) + 3cos(3x), Torga g(x) = 2e-4Ts2 cos(2x) + 3e-9T^ cos(3x).
nocTpouM rpa^uK C TOHHHM pemeHueM oSpaTHon 3agaau u pemeHuaMu C norpemHOCTbro gaa pa3Hbix S u npu e = 0.15, T =1.
9

11.

06paTHaa 3agana 2
PaccMOTpuM Ha^a^bHO-KpaeByro 3aga^y g^a ypaBHeHua Ten.nonpoBogHOCTH c CHHrynapHMM BO3Mym,eHHeM
ut ( x,t) = £2u xx ( x,t), ( x,t ) E Q T , (1) u(0,t) = u(n,t) = 0, 0 < t < T, (2) u(x, 0) = <^(x), 0 <
x < n. (3)
nycTb ^yHKgua <^(x) Heu3BecTHa. TpeSyeTca onpege^HTb <^(x), ec^H 3agaHa gono^HHTe^BHaa HH^opMa^a o pemeHHH 3aga^H (1)-(3)
u(x,T) = g ( x ) , 0 < x < n.
10

12.

Bbreog ^opMy^M gna 03 2
PaccMOTpuM HananbHo-KpaeByro 3agany gna ypaBHeHua TennonpoBogHocTu c CUHrynapHbiM Bo3Mym,eHueM
ut(x,t) = e2u xx ( x , t ) ,
(x,t) e Q T , (1) u(0,t) = u(n,t) = 0, 0 < t < T, (2) u(x, 0) = <^(x), 0 < x <
n. (3)
e - noflo*HTejbHHH Ma^un napaMeTp. PemeHue ^TOH 3aganu 6ygeM o6o3HanaTb u(x, t; e).
npegno^o^HM, nTo ^yHKnua <^(x) ygoBneTBopaeT cnegyromuM ycnoBuaM:
p e C2m+3[0,n], <^(2k)(0) = <^(2k)(n) = 0, k = 0,1,...,m + 1. (4)
Xopomo H3BecTHo, nTo pemeHue 3aganu (1)-(3) uMeeT Bug
^2r n
u ( x , t ; e) = > — i p ( s ) sin ns ds e x p ( - e2n 2 t ) sin n x . (5)
n=1n J
o
npuMeHUB ^opMyny Tennopa u ucnonb3oBaB ycnoBua (4), nonynuM, nTo gna ^yHK-guu
u(x,t; e) cnpaBegnuBo npegcTaBneHue
m
tk
u ( x , t ; e) = <p(x) + ^2 e2kk^(2k)(x) + e2(m+1)vm+i(x, t; e). (6)
k=1
C^opMynupyeM o6parayro 3agany. nycTb ^yHKnua <^(x) Heu3BecTHa. Tpe6yeTca onpegenuTb
<^(x), ecnu 3agaHa gononHUTenbHaa uH^opMagua o pemeHuu 3aganu
(1)-(3):
u ( x , T ; e) = g(x; e), 0 < x < n.(7)
nycTb m =1. YnuTMBaa pa3no*eHue (6), onpegenuM npu6nu:xeHHoe pemeHue o6paraon 3aganu
KaK pemeHue KpaeBon 3aganu
e2T^"(x; e) + <^(x; e) = g(x; e), 0 < x < n,
^(0;e) = ^(n; e) = °.
PemeHue ^TOH 3aganu onpegenaeTca ^opMynon
x
<^(x; e) = e-1T-1/2[sin(e-1T-1/2n)]-1(sin[e-1T-1/2(x—n)] / sin(e-1T-1/2s)g(s; e) ds+
o
sin(e 1T 1/2x) / sin[e 1T 1/2(s — n)]g(s; e) ds)
11

13.

PacneTM gna 03 2
npu6au:*:eHHoe pemeHue 3agaau onpegeaaeTca ^opMyaoii
pX
<p(x; e) = £-1T- [sin(e- T- n)]- (sin[e- T- (x—n)] / sin(e- T- s)g(s; e) ds+
1/2
1
1/2
1
1
1/2
1
1/2
J0
pn
sin(e-1T-1 2x) sin[e-1T-1/2(s — n)]g(s; e) ds)
/
X
gaa noayaeHua pacaeToB nporpaMMHO peaau3yeM onncaHHHH MeTog. gaa ^TO^o
BBegeM ceTKy c maroM h = —, rge n - aucao KopHea nogbiHTerpaabHoa ^yHKnuu
n
Ha oTpe3Ke [0,n] + 2 u goMHo:xeHHoe Ha 5.
nocauTaeM 3HaaeHue ^yHKguu B Ka^goM y3ae ceTKu. gaa ^TO^o B ^opMyay BMecTo x
nogcTaBHM Hamu gucKpeTHbie 3HaaeHua. gaaame no MeTogy Tpanegua cauTaeM
uHTerpaabi, ucnoab3ya Ty *e ceTKy.
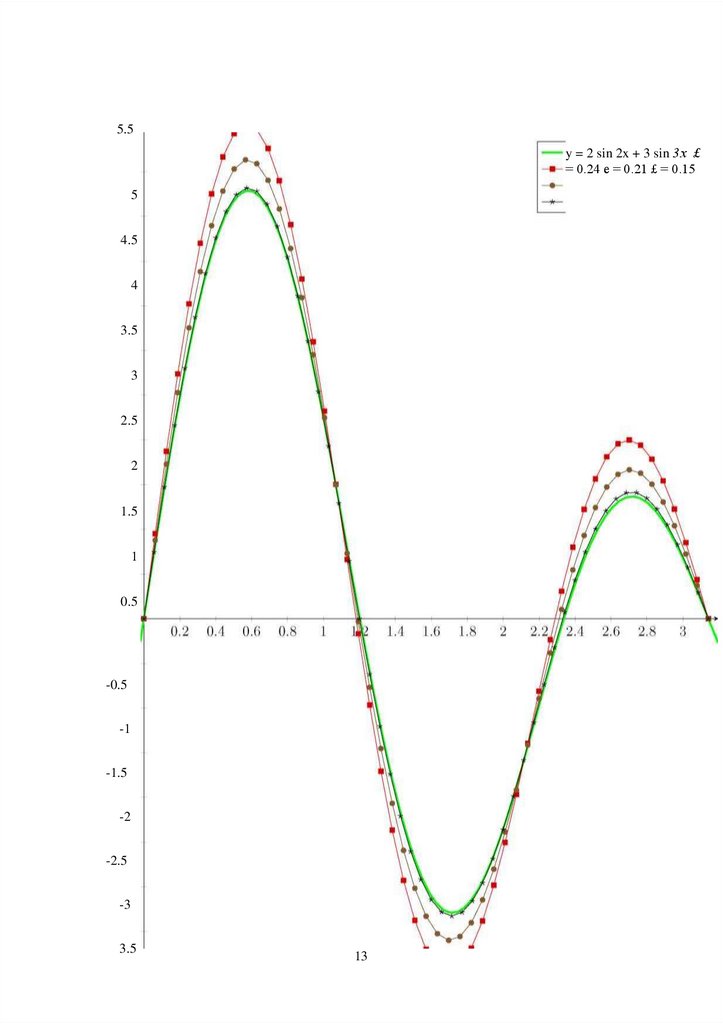
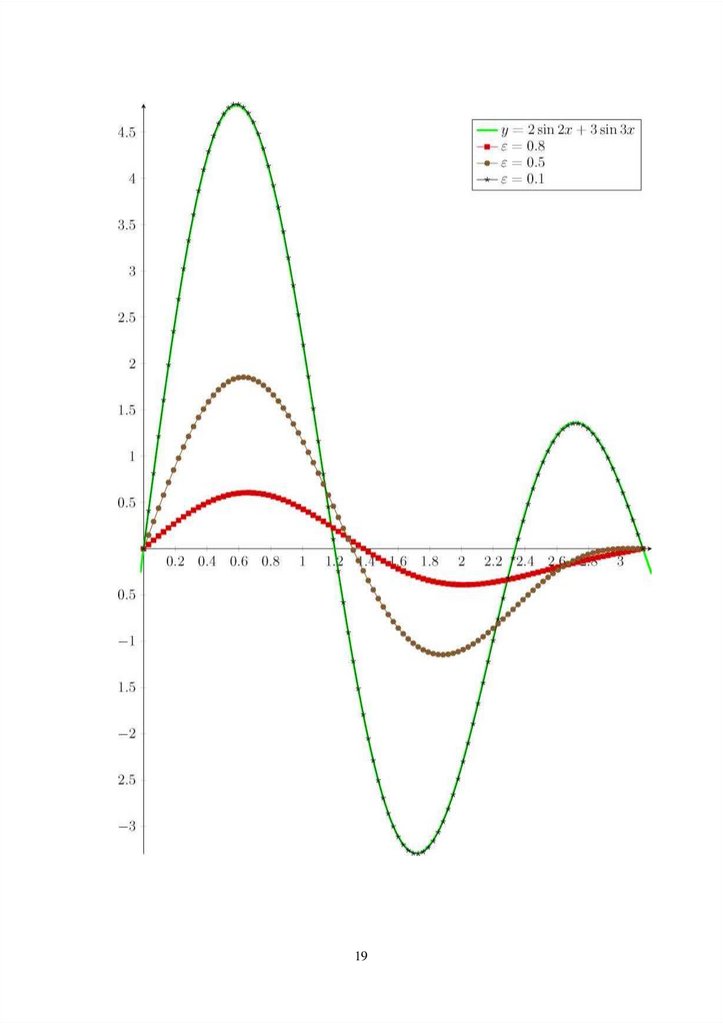
npoTecTpuyeM nporpaMMy. Bo3bMeM <^(x) = 2sin(2x) + 3sin(3x), Torga g(x) = 2e-4T^ sin(2x) +
3e-9T^ sin(3x).
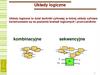
nocTpouM rpa^uK c TOHHMM pemeHueM odparaon 3agaau u npu6au:xeHHbiMu pe-meHuaMu
gaa pa3Hbx e u npu T =1. no HeMy MOXHO cgeaaTb Bbmog, aTo gaa MeHbmero e
npu6au:xeHHoe pemeHue ayame, a gaa Soaamero e npu6au:xeHHoe pe-meHue cuabHo
oTauaaeTca OT ToaHoro.
12

14.

5.5
y = 2 sin 2x + 3 sin 3x £
= 0.24 e = 0.21 £ = 0.15
5
4.5
4
3.5
3
2.5
2
1.5
1
0.5
-0.5
-1
-1.5
-2
-2.5
-3
3.5
13

15.

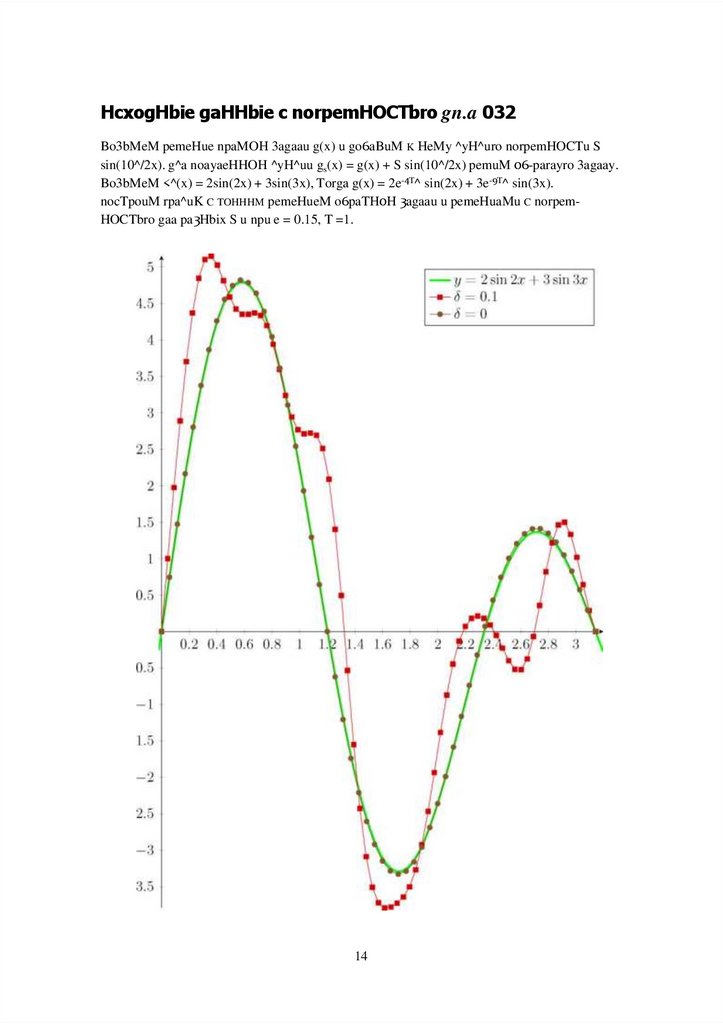
HcxogHbie gaHHbie c norpemHOCTbro gn.a 032
Bo3bMeM pemeHue npaMOH 3agaau g(x) u go6aBuM K HeMy ^yH^uro norpemHOCTu S
sin(10^/2x). g^a noayaeHHOH ^yH^uu gs(x) = g(x) + S sin(10^/2x) pemuM 06-parayro 3agaay.
Bo3bMeM <^(x) = 2sin(2x) + 3sin(3x), Torga g(x) = 2e-4T^ sin(2x) + 3e-9T^ sin(3x).
nocTpouM rpa^uK C TOHHHM pemeHueM o6paTH0H 3agaau u pemeHuaMu C norpemHOCTbro gaa pa3Hbix S u npu e = 0.15, T =1.
14

16.

06paTHaa 3agana 3
PaccMOTpuM Ha^a^bHO-KpaeByro 3aga^y g^a ypaBHeHua Ten.nonpoBogHOCTH c CHHrynapHMM BO3Mym,eHHeM
u t ( x , t ) = £ 2 u x x ( x , t ) + f ( x ) p ( t ) , (x,t) e Q T , (1) u(0,t) = u ( n , t ) = 0, 0 < t < T,
(2) u(x, 0) = 0, 0 < x < n. (3)
nycTb ^yHKnua f (x) Heu3BecTHa. TpeSyeTca onpege^HTb f (x), earn H3Becraa p(t) H
3agaHa gono^HHTe^BHaa HH^opManga O pemeHHH 3aga^H (1)-(3)
u ( x , T ) = g(x), 0 < x < n.
15

17.

Bbreog ^opMy^M gna 03 3
PaccMOTpuM HananbHo-KpaeByro 3agany gna ypaBHeHua TennonpoBogHocTu c CUHrynapHbiM Bo3Mym,eHueM
ut(x,t) = £ 2 u xx (x,t) + f (x)p(t), (x,t) e QT, (1) u(0,t) = u(n,t) = 0, 0 < t < T, (2) u(x, 0) = 0, 0 <
x < n. (3)
e - noflo*HTejbHHH Ma^un napaMeTp. PemeHue ^TOH 3aganu 6ygeM o6o3HanaTb u ( x , t ;
e). Xopomo u3Becrao, nTo pemeHue 3aganu (1)-(3) uMeeT Bug
^ „t
u(x, t; e) =
f n / e - ^ n2(t—T V(r) dr sin nx, (4)
n=1 ^
rge
2r
fn = - f (s) sin nsds .
n ./ °
npegnono^uM, nTo ^yHKnua f (x) ygoBneTBopaeT rregymmuM ycnoBuaM:
f G c2m+3[0,n], f(2k)(0) = f(2k)(n) = 0, k = 0,1,...,m + 1. (5)
a p e C[0, T].
npouHTerpupoBaB no nacTaM uHTerpanui, Bxogamue B ^opMyny (4), nonynuM cnegyrom,ee npegcTaBneHue:
m
u ( x , t ; e) = ^ e 2 k f ( 2 k \ x ) p k (t) + e2(m+1)Vm+i(x, t; e). (6)
k= °
rge
Pk (t) = J (t-f^p(T)dr, k
0,^..^m
a
vm+1(x t; e) = (-1)m+1 ^ f
2(m+1)
nn
°
n=1
t —£ 2 n 2 (t- T )
pm(r) dr sin nx.
e
C^opMynupyeM o6parayro 3agany. nycTb ^yHKnua p(t) 3agaHa, a f (x) Heu3BecTHa.
Tpe6yeTca onpegenuTb f (x), ecnu 3agaHa gononHuTenbHaa uH^opMagua o peme-HUU
3aganu (1)-(3):
u(x,T; e) = g(x; e), 0 < x < n.(7)
nepengeM K nocTpoeHuro npu6nu:xeHHoro pemeHua B cnynae m =1. OnpegenuM
npu6nu*eHHoe pemeHue o6paraon 3aganu KaK pemeHue KpaeBon 3aganu
16

18.

eV(T)/"(x) + po(T)/(x) = g(x; e) 0 < x < n /(0) = f (n) = °.
npu aHagu3e ^Toft 3aganu Hyx:HO paccMaTpuBaTb Tpu cgynaa: pl(T)p0(T) > 0,pl(T)p0(T) < 0,Pi(T
)po(T) = 0.
O^eBugHO, ^TO nepBMH ony^aft aHagoru^eH oSparaoft 3agage 1.
PaccMOTpuM BTopofi cgynafi: pl(T)p 0 (T ) < 0.
PemeHue ^TOH 3agagu onpegegaeTca ^opMyaofi
/(x) = (e(-popi)l/2 sh(e l(-—)l/2n)) l
PI
(sh[e-l(——)l/2(x — n)] / sh(e-l(——)l/2s)g(s; e) ds + PI Jo PI
x
pn
sh(e-l(——)l/2x) / sh[e-l(——)l/2(s — n)]g(s; e) ds) PI Jx PI
nepefigeM K TpeTteMy cayaaro pl(T)p0(T) = 0. BO3MO*HM Tpu BapuaHTa. B
nepBOM pl (T) = 0, p0(T) = 0. Torga pemeHue onpegegaeTca ^opMynofi
/(x) =
g(x;e)
p0(T)
BO BTOPOM p0(T) = 0, pl(T) = 0 u pemeHue noayaaeM u3 ^opMyn
/(x)
1
e2pl(T)
(x
g(x; e)dx
xg(x; e)dx + Clx + C2).
f (0) = f (n) = 0.
TpeTufi cayaafi p0(T) = 0, pl(T) = 0 gga nocTpoeHua npuSgu^eHHoro pemeHua aBaaeTca
Seccogep^aTegtHMM.
17

19.

PacneTM gna 03 3
Bo3bMeM f (x) =
Torga po(T) = T
2sin(2x) + 3sin(3x), p(t) = 1 — t.
T 2 . . T2 T3 . . . £2(-4e-4e2T
- ~ 2 ~ , p I ( T ) = -2—^ , 9 ( x ) =2sin(2x)-
4T + 4) - e-4e2T + 1 16£4
2
-9e2T - 9T + 9) - e-9e2T + 1
Q . ,Q ,£ (-9e
+3 sin(3x)-8T£4-.
Earn B3STb T = 2.5, TO nepeageM K onyaaro pi(T)p0(T) < 0. PemeHue ^Toa 3agaau
onpegeaaeTca ^opMyaoa
f (x) = (£(-poPi)1/2 sh(£ 1(- — )1/2n)) 1
P1
x
(sh[£-1(-—)1/2(x - n)\ / sh(£-1(-—)1/2s)g(s; £) ds + P1
Jo P1
pn
sh(£-1(-—)1/2x) / sh[£-1(-—)1/2(s - n)\g(s; £) ds) P1 dx
P1
gaa noayaeHaa pacaeToB nporpaMMHO peaaa3yeM onncaHHHH MeTog. g.na ^TO^o
h n
BBegeM ceTKy c maroM h = .
nocauTaeM 3HaaeHue ^yH^aa B Ka^goM y3ae ceTKu. gaa ^TO^o B ^opMygy BMecTo x
nogcTaBHM Hama gacKpeTHbie 3HaaeHua. gaabme no MeTogy Tpanegaa cauTaeM
HHTerpa^M, acnoab3ya Ty *e ceTKy. npoTecTpuyeM nporpaMMy, gaa pa3Hbix £ nogyaaeM:
18

20.

19

21.

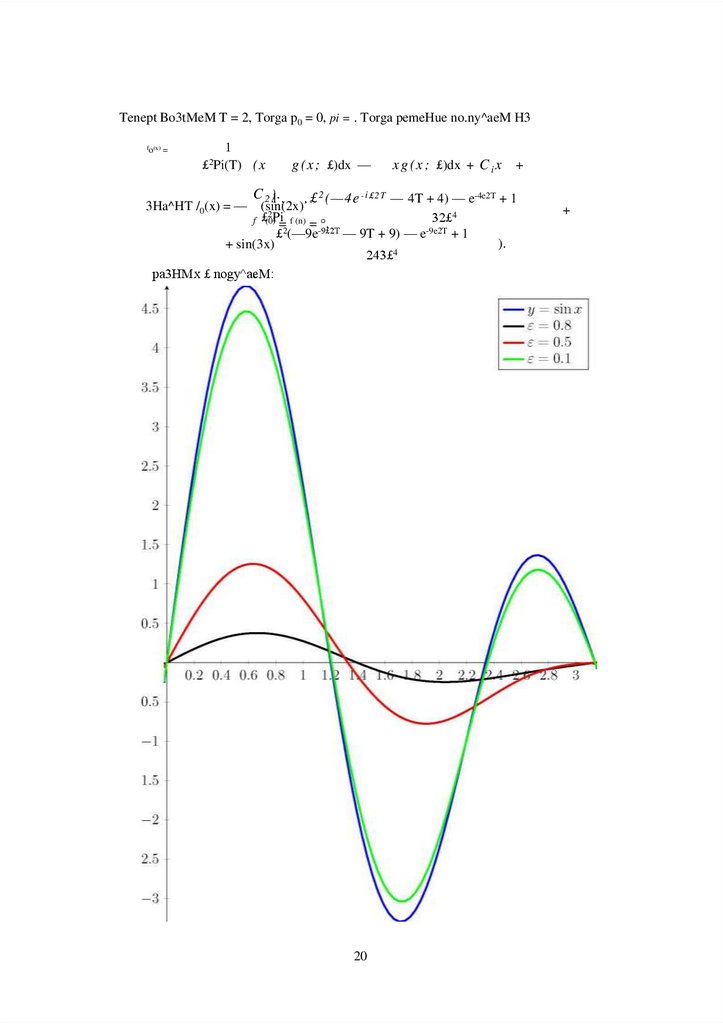
Tenept Bo3tMeM T = 2, Torga p0 = 0, pi = . Torga pemeHue no.ny^aeM H3
fo(x) =
1
£2Pi(T)
(x
g ( x ; £)dx —
x g ( x ; £)dx + C i x +
C 2 )1. , . , £ 2 (—4 e - i £2T — 4T + 4) — e-4e2T + 1
3Ha^HT /0(x) = — (sin(2x)
2
32£4
f £(0)Pi= f (n) = °.
2
-9£2T
-9e2T
£ (—9e
— 9T + 9) — e
+1
).
+ sin(3x)
4
243£
pa3HMx £ nogy^aeM:
20
+

22.

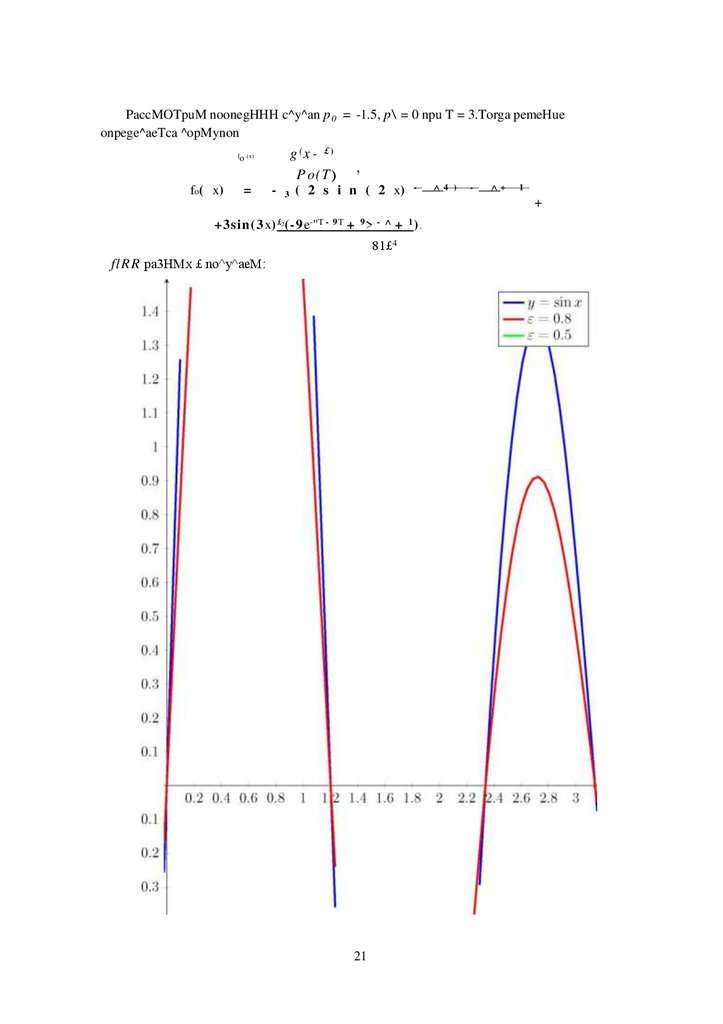
PaccMOTpuM noonegHHH c^y^an p 0 = -1.5, p\ = 0 npu T = 3.Torga pemeHue
onpege^aeTca ^opMynon
fo (x)
fo( x)
=
g (x - £)
P o( T )
’
- 3 ( 2 s i n ( 2 x) -
+3sin(3x) £2(-9e-"T - 9 T + 9 > - ^ + 1 ) .
81£4
flRR pa3HMx £ no^y^aeM:
21
^4 )
-
^+
1
+

23.

PaccMOTpuM cnyaan p 1 ( T ) p o( T ) < 0.
PemeHue ^TOH 3agaau onpegenaeTca ^opMynon
f (x) = (e(-poPi)1/2 sh(e 1(-—)1/2n))x
\-i
PI
(sh[e-1(—p0)1/2(x — n)\ f sh(e-1(—p0)1/2s)g(s; e) ds +
pi Jo P1pn
sh(e 1(——) 1 2 x) sh[e-1(——) 1 2 (s — n)\g(s ; e) ds)
/
/
p1
p1
^na nonyaeHua pacaeToB nporpaMMHO peanu3yeM onncaHHHH MeTog. flns ^TO^o
n
BBegeM ceTKy c maroM hh^^59.
nocauTaeM 3HaaeHue ^yHKnuu B Ka^goM y3ne ceTKH. ^na ^TO^o B ^opMyny BMecTO x
nogcTaBHM Hama gncKpeTHbie 3HaaeHua. flanbme no MeTogy Tpane^n cauTaeM
HHTerpanM, ncnonn3ya Ty *e ceTKy.
3n
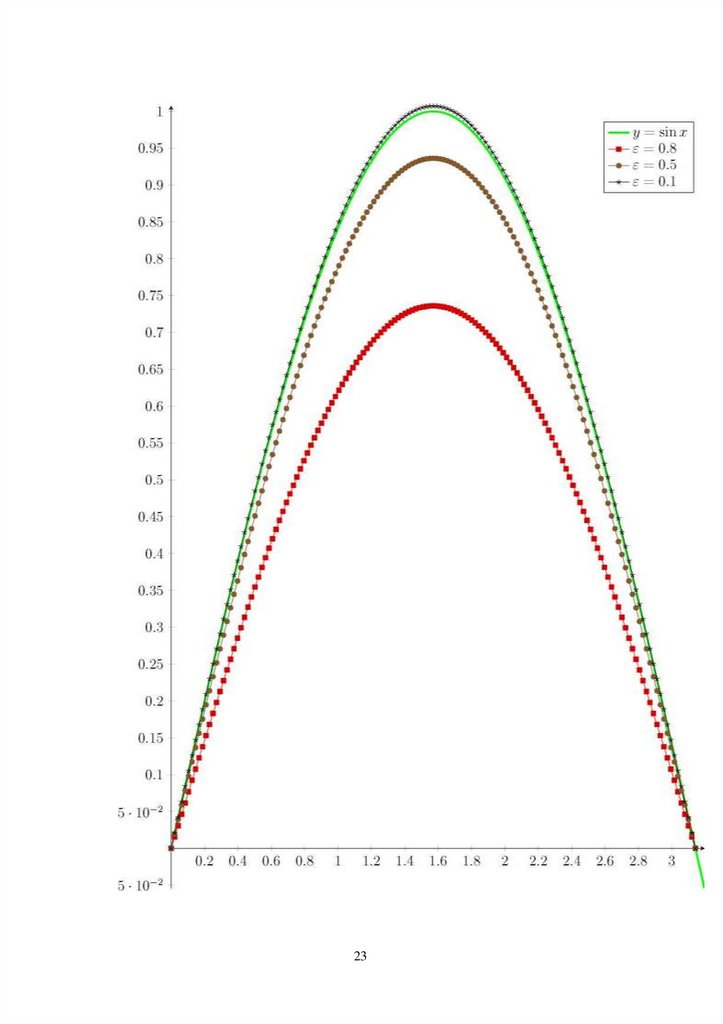
npoTecTpuyeM nporpaMMy. Bo3bMeM p ( t ) = cos(2t ) , f ( x ) = sin(x),T = —, Torga
. , . 2 sin(2T)+ e2 cos(2T) — e 2 e ~ T £2
p 0 = — 0.5,p1 = 0.25, g(x) = sin(x)e4 + 4
^na pa3Hbx e nonyaaeM
22

24.

23

25.

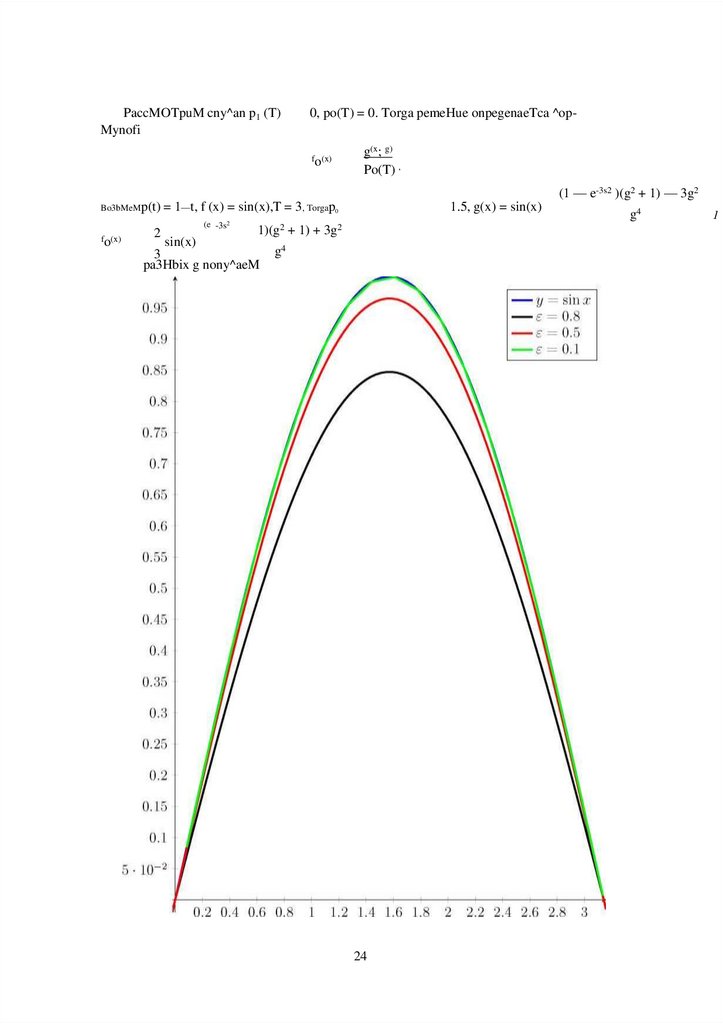
PaccMOTpuM cny^an p1 (T)
Mynofi
0, po(T) = 0. Torga pemeHue onpegenaeTca ^op-
fo(x)
g(x; g)
Po(T) ,
(1 — e-3s2 )(g2 + 1) — 3g2
Bo3bMeMp(t) = 1—t, f (x) = sin(x),T = 3, Torgap0
fo(x)
2
(e -3s2
1.5, g(x) = sin(x)
1)(g2 + 1) + 3g2
sin(x)
3
pa3Hbix g nony^aeM
g4
24
g4
1

26.

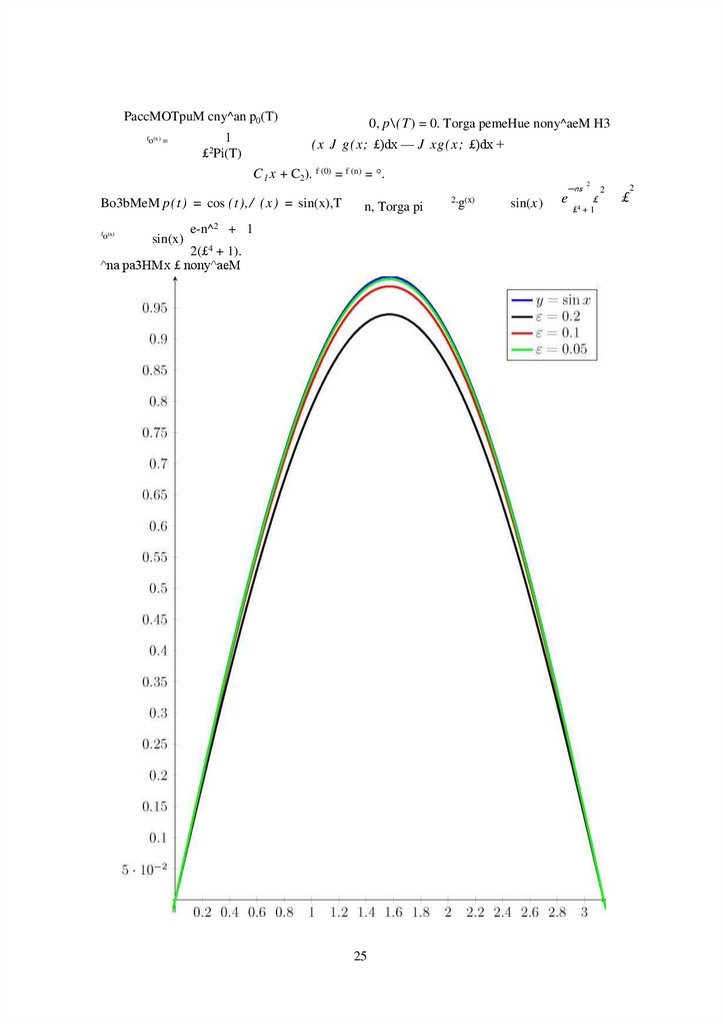
PaccMOTpuM cny^an p0(T)
fo(x) =
1
£2Pi(T)
0, p\(T ) = 0. Torga pemeHue nony^aeM H3
(x J g(x; £)dx — J xg(x; £)dx +
C 1 x + C2). f (0) = f (n) = °.
—ns
Bo3bMeM p(t) = cos (t),/ (x) = sin(x),T
fo(x)
sin(x)
n, Torga pi
e-n^2 + 1
2(£4 + 1).
^na pa3HMx £ nony^aeM
25
2,g(x)
sin(x )
e
2
£
£4 + 1
2
£
2

27.

CnucoK ^HTepaTypbi
[1] ^eHHCOB A.M. BBegeHue B Teopuro o6parabix 3aga^. M.: Mry, 1994.
[2] ^eHHCOB A.M. npuS^u^eHHoe pemeHue o6paTHbix 3aga^ g^a ypaBHeHua
TenaonpoBogHOCTu c cuHryaapHbiM B03Mym,eHueM. M.: Mry, 2021.
[3] ^eMugoBu^ B.n., MapoH H.A. OCHOBM BbiaucauTeabHOH MaTeMaTUKu. — 2. —
Ou3-MaT. 4UT., 1963.
[4] CaMapcKun A.A., Ba6um,eBua n.H. MuoneHHbie MeTogbi pemeHua o6paTHbix
3agaa MaTeMaTuaecKOH ^U3UKU. M.: EguTopuaa yPCC, 2004.
26