Similar presentations:
Графики и свойства функций
1.
ГРАФИКИ И СВОЙСТВАФУНКЦИЙ
2.
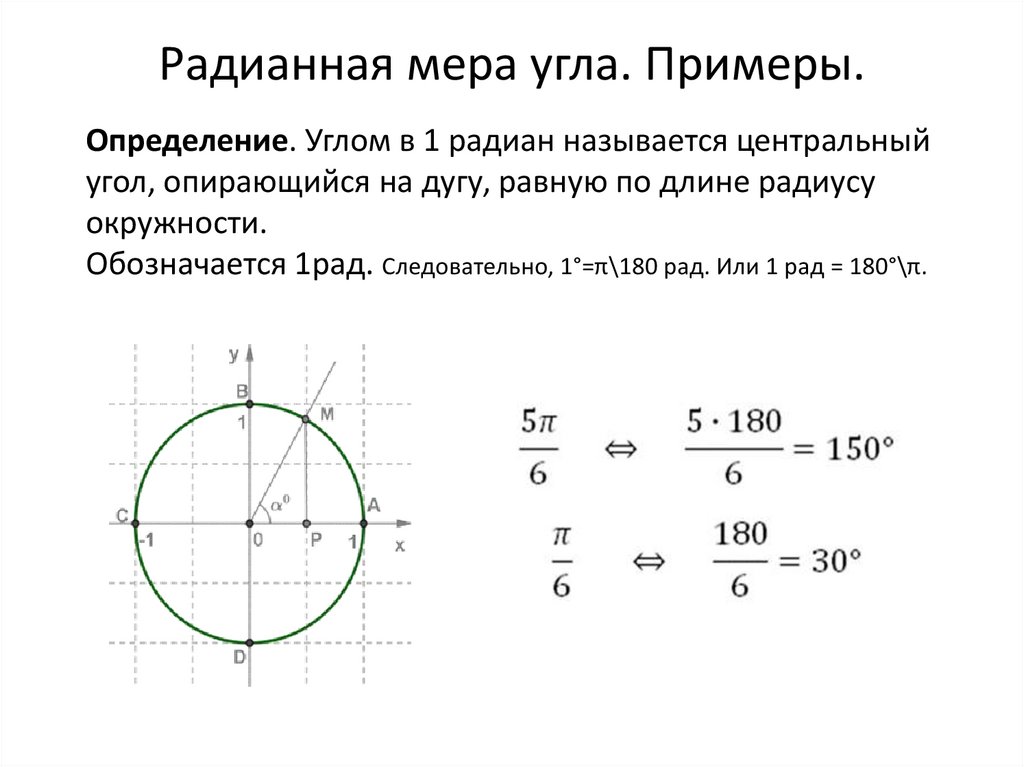
Радианная мера угла. Примеры.Определение. Углом в 1 радиан называется центральный
угол, опирающийся на дугу, равную по длине радиусу
окружности.
Обозначается 1рад. Следовательно, 1°=π\180 рад. Или 1 рад = 180°\π.
3.
Тригонометрические функции: определениесинуса и косинуса угла
Синус острого угла в прямоугольном треугольнике –
это отношение противолежащего катета к гипотенузе.
sin∠A=BC/AB.
Косинус острого угла в прямоугольном треугольнике –
это отношение прилежащего катета к гипотенузе.
cos∠A=АC/AB.
4.
Тригонометрические функции: определениетангенса и котангенса угла
Тангенс острого угла в прямоугольном треугольнике –
это отношение противолежащего катета к прилежащему.
tg∠A=ВC/AС.
Котангенс острого угла в прямоугольном
треугольнике – это отношение прилежащего катета к
противолежащему.
сtg∠A=АC/ВС.
5.
Соотношения между тригонометрическими функциямиодного и того же угла.
6.
Основные тригонометрические тождества1.
7.
Понятие функции. Основныеэлементарные функции.
Определение: Функцией y = f (x) называется
зависимость переменной У от переменной Х
такая, что для любого значения Х существует
единственное значение У.
• У-зависимая переменная –функция.
• Х-независимая переменная –аргумент
• Множество значений Х образует
ОБЛАСТЬ ОПРЕДЕЛЕНИЯ функции.
• Множество значений У образует
ОБЛАСТЬ ЗНАЧЕНИЯ функции.
8.
9.
10.
11.
Определение:Числовые функции,
заданные формулами
у=sin x и y = cos x,
называют соответственно
синусом и косинусом.
12.
y=sin xу
1
-π/2
-3π/2
-π
π
0
-1
π/2
2π
3π/2
3π
5π/2
х
13.
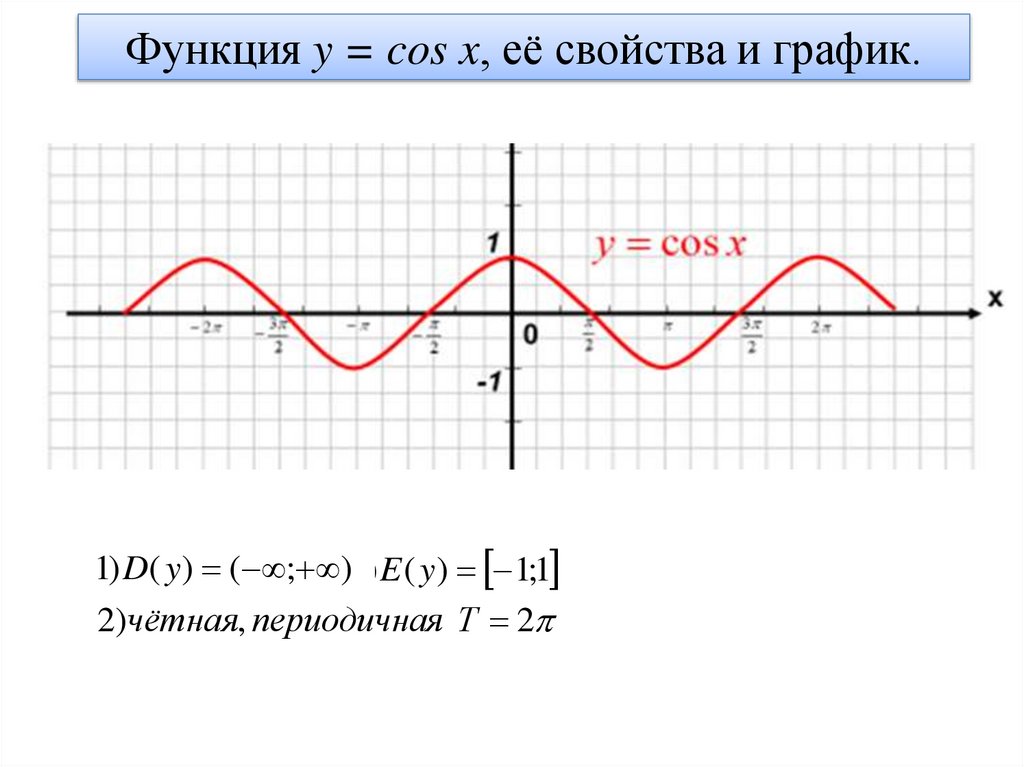
Функция y = cos x, её свойства и график.1) D( y ) ( ; )
2)чётная, периодичная Т 2
3) Возрастает на ;0
2
4) Убывает на 0;
2
1) D( y ) ( ; )5) E ( y ) 1;1
2)чётная, периодична
я Т 2
6) ограничена
7) yнаим
1
3) Возрастает на ;0
2 1
yнаиб
14.
Определение:Функция вида y=xn, где n-любое
действительное число называют
степенной функцией.
15.
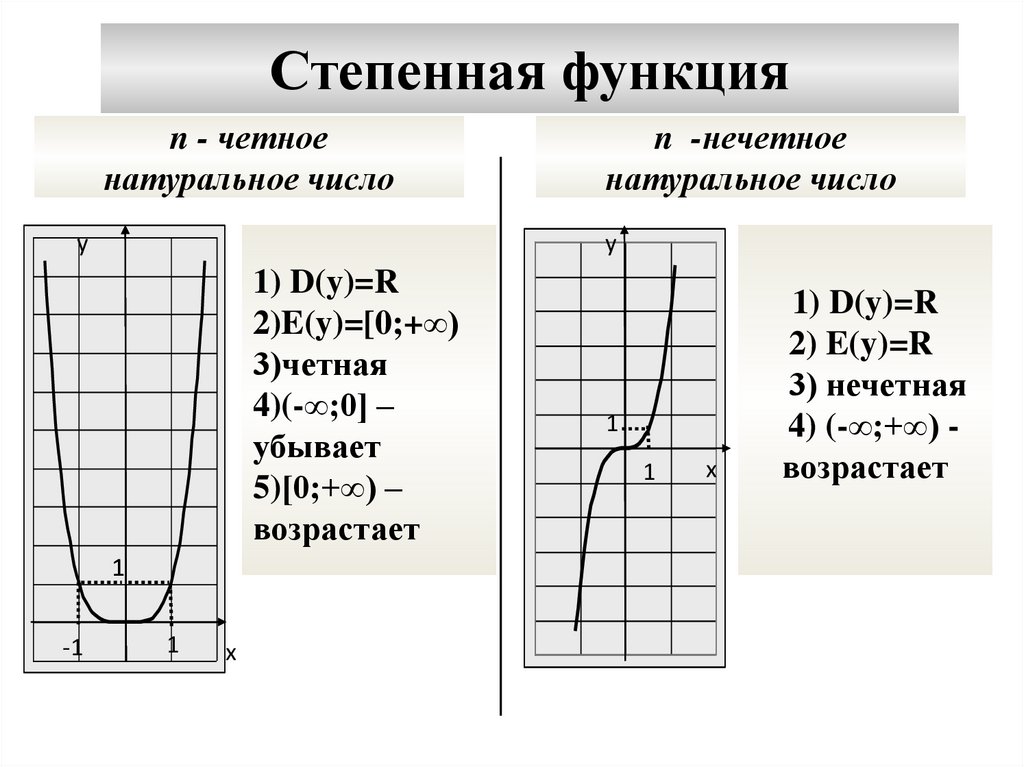
Степенная функцияn - четное
натуральное число
у
у
1) D(y)=R
2)E(y)=[0;+∞)
3)четная
4)(-∞;0] –
убывает
5)[0;+∞) –
возрастает
1
-1
n -нечетное
натуральное число
1
х
1
1
х
1) D(y)=R
2) E(y)=R
3) нечетная
4) (-∞;+∞) возрастает
16.
Степенная функцияn - четное
натуральное число
у
у
1) D(y)=R
2)E(y)=[0;+∞)
3)четная
4)(-∞;0] –
убывает
5)[0;+∞) –
возрастает
1
-1
n -нечетное
натуральное число
1
х
1
1
х
1) D(y)=R
2) E(y)=R
3) нечетная
4) (-∞;+∞) возрастает
17.
Определение:Функция вида y x ,где n-любое
n
действительное число называют
иррациональной функцией.
18.
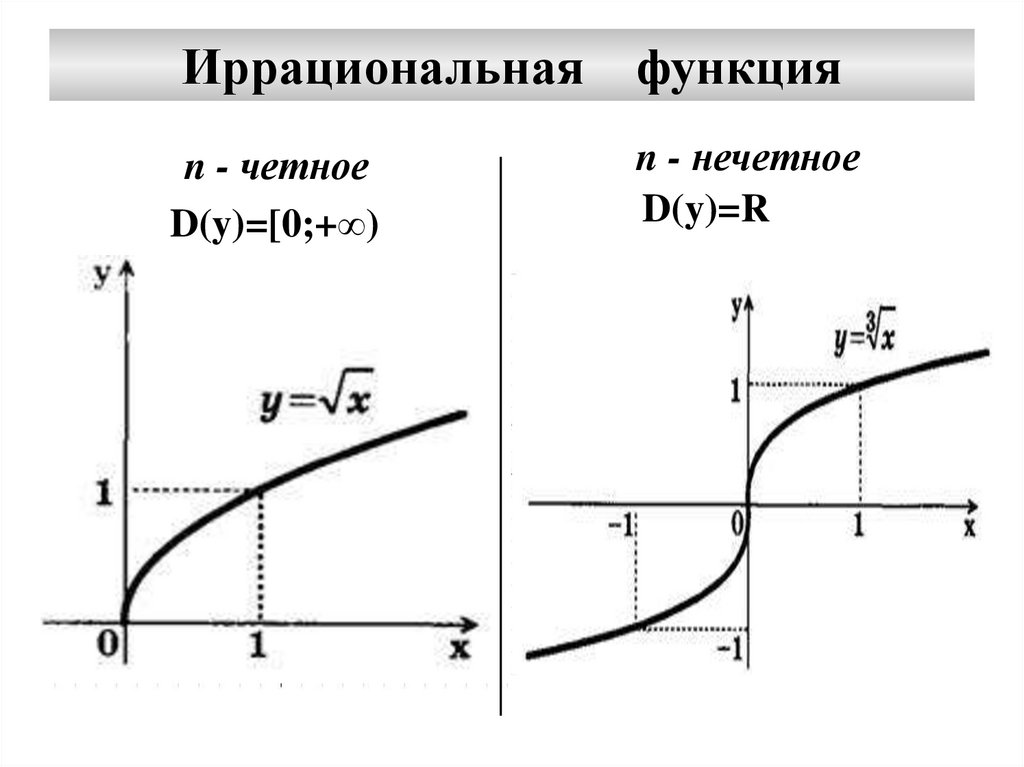
Иррациональнаяфункция
n - четное
D(y)=[0;+∞)
n - нечетное
D(y)=R
R
• 2)E(y)=[0;+∞)
19.
20.
Определение:Показательной функцией
называется – функция вида
y a
x
a >0, a 1
где x – переменная,
a – заданное число
21.
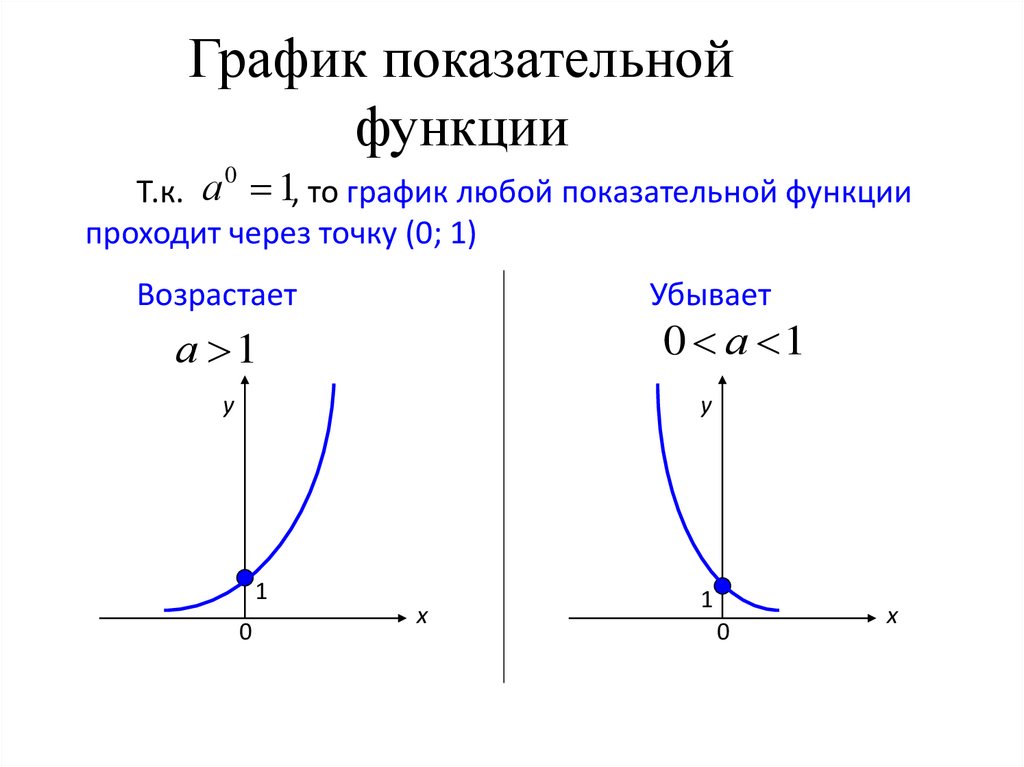
График показательнойфункции
Т.к. а 1, то график любой показательной функции
проходит через точку (0; 1)
0
Возрастает
Убывает
0 а 1
а 1
у
у
1
0
х
1
0
х
22.
Свойства показательной функцииn - четное
натуральное число
у
у
1) D(y)=R
2)E(y)=[0;+∞)
3)четная
4)(-∞;0] –
убывает
5)[0;+∞) –
возрастает
1
-1
n -нечетное
натуральное число
1
х
1
1
х
1) D(y)=R
2) E(y)=R
3) нечетная
4) (-∞;+∞) возрастает
23.
Определениелогарифма
Логарифмом положительного числа b по
основанию a, а>0, a≠1, называется
показатель степени в которую надо возвести
число a, чтобы получить число b.
log a b х
а b
х
24.
Определение:Логарифмической
функцией называется –
функция вида
у = logax a >0, a 1
где x – переменная,
a – заданное число
25.
у = log хвозрастает
при a > 1;
a
y = log х
убывает
при 0 < a < 1;
a
1
26.
Свойства логарифмовЛогарифм единицы
log a 1 0
log a a 1
Логарифм произведения
положительных чисел
log a xy log a x log a y
Логарифм частного
положительных чисел
x
log a log a x log a y
y
Логарифм степени
положительных чисел
log a a n
n





















 mathematics
mathematics








