Вклад Франсуа Виета в решение кубических уравнений. Исследовательская работа по математике

1.

Вклад Франсуа Виета в решение
кубических уравнений
Исследовательская работа
по математике
Ученицы 11 «А» класса МОУ «Лингвистическая
гимназия № 23 им. А. Г. Столетова г. Владимира»
Гурьяновой Наны

2.

Объектная область
исследования –
математика.
Объект исследования кубические уравнения
Предмет исследования
– история поиска формул
для решения кубических
уравнений.

3.

Цель:
установить вклад
Франсуа Виета в
решение вопроса о
нахождении общего
способа решения
кубических
уравнений.
Гипотеза:
Значим ли вклад Франсуа
Виета в решение
кубических уравнений при
условии того, что общий
метод решения
исследовался многими
математиками?

4.

Задачи:
Изучить литературу по
данному вопросу;
Выяснить историю
кубических уравнений;
Проанализировать
деятельность
математиков, работающих
с данными уравнениями;
Составить список
европейских математиков,
исследовавших
кубические уравнения;

5.

Задачи:
Проанализировать
деятельность Франсуа
Виета;
Оценить вклад Ф.Виета в
решение кубических
уравнений;
Сравнить различные
способы решения
кубических уравнений;
Обобщить изученные
материалы.
Методы исследования:
Анализ и синтез
Сравнение
Обобщение

6.

Истории поиска формул для решения
алгебраических уравнений европейскими
математиками
Леонардо из Пизы (Фибоначчи) (1220 г.)
Доказал, что корни уравнения
х 3 + 2х 2 + 10х = 20 нельзя выразить с
помощью евклидовых
иррациональностей вида а+ в .
Лука Пачоли
(1494 г.)
В книге «Сумма знаний» писал, что
решение уравнений х 3 + рх = q,
х 3 + q = рх столь же невозможно при
современном ему состоянию науки,
как и квадратура круга.
Сципион Даль Ферро
( 1515 г.)
Нашел способ решения уравнения
х 3 + рх = q, т.е. х 3 + рх + q = 0 с р >
0 и q < 0.
Никколо Тарталья (Фонтана)
(1535 г.)
Изобрел способ решения х
q.
Джироламо Кардано
Нашел решение уравнения
3
+ рх =

7.

Джироламо Кардано
(знал тайну Никколо Тартальи)
(1545 г.)
Лудовико Феррари (ученик
Кардано ) (1547 г.)
Нашел решение уравнения
х3 + рх + q = 0 и в том случае, когда р < 0,
а q > 0.
Нашел способ решения кубического уравнения
с членом второй степени.
Открыл формулы для решения уравнений
четвертой степени.
Франсуа Виет
(1540 – 1603)
Открыл формулы, выражающие коэффициенты
приведенного квадратного трехчлена и
кубического многочлена через их корни.
Паоло Руффини
( 1765 – 1822) и
Нильс Хенрик Абель
(1802 – 1829)
Доказали, что уравнения пятой и более высоких
степеней не имеют общего решения в
радикалах.
Эварист Галуа
(1811 – 1832)
Открыл способ, позволяющий по данному
уравнению определить, имеет ли оно решение
в радикалах.

8.

Выводы:
Существует тесная зависимость между
математикой и общекультурными устремлениями
каждой эпохи.
Арабские математики внесли особенно
значительный вклад в области алгебры.
Самая важная роль в развитии западной
математики принадлежит античной греческой
цивилизации.
Усилиями математиков разных европейских стран в
16 веке был решен вопрос об общем способе решения
кубических уравнений.

9.

Франсуа ́Вие́т
(1540 — 1603)
Выдающийся французский
математик, один из
основоположников алгебры.
По образованию и основной
профессии — юрист. Около
1570 года подготовил
«Математический Канон» —
труд по тригонометрии, —
который издал в Париже в
1579 году. Ввёл буквенные
обозначения для
коэффициентов уравнения и
неизвестных величин.

10.

Вклад Франсуа Виета в решение кубических
уравнений
Кубическое уравнение — полиномиальное уравнение третьей
степени, канонический вид которого ax³ + bx² + cx + d = 0,
где а ≠ 0.
Уравнение можно привести к более простому(каноническому)
виду: y³ + py + q = 0, где p = - b²/3a² + c/a, q = 2b³/27a³ – bc/3a² +d/a
Заменяя x новым y, связанным с x равенством х = у – b/3a.
Величина q2/4 + p3/2 называется дискриминантом кубического
уравнения х3 + pх + q = 0.
Если q2/4 + p3/27 > 0, то уравнение имеет один действительный
корень.
Если q2/4 + p3/27 = 0, то уравнение имеет кратный (совпадающий)
корень

11.

Вклад Франсуа Виета в решение кубических
уравнений
Если q2/4 + p3/27 < 0, то уравнение имеет три
действительных корня.
Случай q2/4 + p3/27 < 0 называется неприводимым, т.
к. если искать корни уравнения по формуле Кардано,
то возникает необходимость извлекать квадратный
корень из отрицательного числа q2/4 + p3/27. Значит
невозможно решить это уравнение, оставаясь в области
действительных чисел.

12.

Вклад Франсуа Виета в решение кубических
уравнений
Франсуа Виет, воспользовавшись формулой cos3α = 4 cos3 α - 3 cosα,
нашел решение для неприводимого случая в тригонометрических
функциях.Это решение эквивалентно извлечению кубических корней из
комплексных чисел.
В 1593 году Фразсуа Виет доказал, что любое кубическое уравнение
можно свести либо к удвоению куба, либо к трисекции угла.
Франсуа Виет выяснил как связаны коэффициенты кубического
многочлена x3 + аx2 + bx + c с его корнями х1, х2, х3.
Знаменитые «формулы Виета» для коэффициентов многочлена как
функций его корней:
а = - (х1 + х2 + х3),
b = х1х2 + х2х3 + х3х1,
c = - х1 х2 х3.

13.

Выводы к второй главе:
Франсуа Виет внес большой вклад в решение
кубических уравнений:
установил связь коэффициентов кубического
многочлена с его корнями;
доказал, что любое кубическое уравнение можно
свести либо к удвоению куба, либо к трисекции
угла;
нашел решение для неприводимого случая в
тригонометрических функция.

14.

Примеры решения кубических уравнений
х3 - 19х + 30 = 0
Первый способ. По теореме Безу.
По теореме Безу, многочлен f(x) делится без остатка на двучлен х-а
только тогда, когда а является корнем уравнения.
Любой целый корень с целыми коэффициентами является делителем его
свободного числа.
1. Найдём все целые делители свободного члена уравнения:
+1,-1, +2, -2, +3, -3, +5, -5, +6, -6, +10 -10.
2. Непосредственной проверкой убеждаемся, что х=2 — корень
уравнения.
3. Делим многочлен х3 - 19х + 30 на двучлен х-2, в частном получится
х² + 2х - 15.
4. Разложим многочлен на множители: (х² + 2х - 15)(х-2)
5. Найдём корни уравнения (х² + 2х — 15)(х-2)=0: x1=3, х2=-5, х3=2
По основной теореме алгебры многочлен степени n имеет не более n
различных корней. Значит мы нашли все имеющиеся корни.

15.

Примеры решения кубических уравнений
х3 - 19х + 30 = 0
Второй способ. По формуле Кардано.
p = -19, q = 30.
Подставляем в формулу числа p и q.
 
3
x= −
 
3
30
30 2 −19 3
30
30 2 −19 3
 

 − − 


2
4
27
2
4
27
Так как 30²/4 + (-19)³/27 < 0, то мы не можем продолжить решение
без использования комплексных чисел.

16.

Примеры решения кубических уравнений
х3 - 19х + 30 = 0
Третий способ. Графический.
Педставим уравнение в виде х³= 19х - 30 и рассмотрим две функции:
у = х³ и у = 19 - 30.

17.

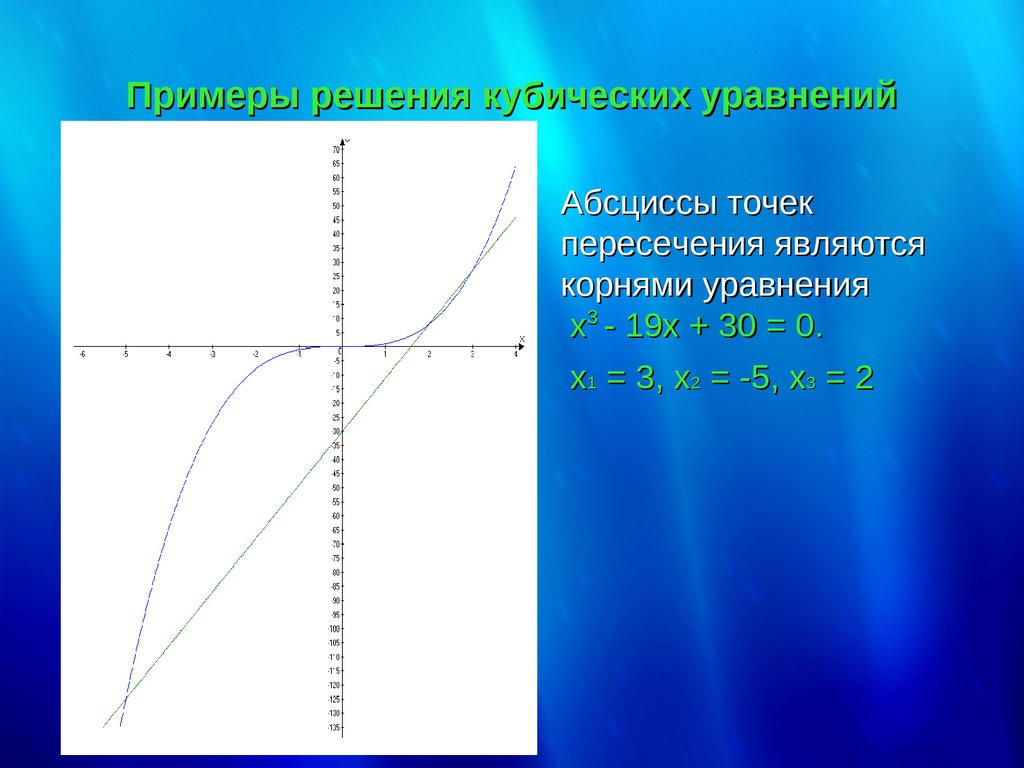
Примеры решения кубических уравнений
Абсциссы точек
пересечения являются
корнями уравнения
х3 - 19х + 30 = 0.
х1 = 3, х2 = -5, х3 = 2

18.

Выводы к третьей главе:
Применение формулы Кардано к решению кубических
уравнений часто приводит к громоздким, не поддающимся
алгебраическим преобразованиям, выражениям. Это очень
снижает их практическую значимость.
Известные в школьном курсе методы (разложение на
множители, графический метод) гораздо приятнее
применять к решению кубических уравнений.
Поиски общей формулы решения кубических уравнений и
ее исследование дали мощный импульс для развития
современной алгебры, определили на многие годы вперед
пути ее развития.

19.

Заключение:
Проведенное исследование помогло выяснить:
Историю кубических уравнений.
Проанализировать деятельность математиков,
работающих с данными уравнениями.
Составить список европейских математиков, исследовавших
кубические уравнения.
Проанализировать деятельность и оценить вклад Франсуа
Виета в решение кубических уравнений.
Сравнить различные способы решения кубических уравнений.
Французский математик Франсуа Виет решил так
называемый «неприводимый» случай в тригонометрических
функциях, тем самым, внеся большой вклад в решение
кубических уравнений.