Similar presentations:
Сравнение двух групп и множественные сравнения. Лекция 6
1. ЛЕКЦИЯ 6
x1 x2t
sx1 x2
СРАВНЕНИЕ ДВУХ ГРУПП И
МНОЖЕСТВЕННЫЕ
СРАВНЕНИЯ
2. 6.1. Принцип теста Стьюдента (t-теста)
3. Схема испытания диуретического действия препарата Х
10 добровольцевПРЕПАРАТ
ПЛАЦЕБО
4. Результат испытания действия диуретика
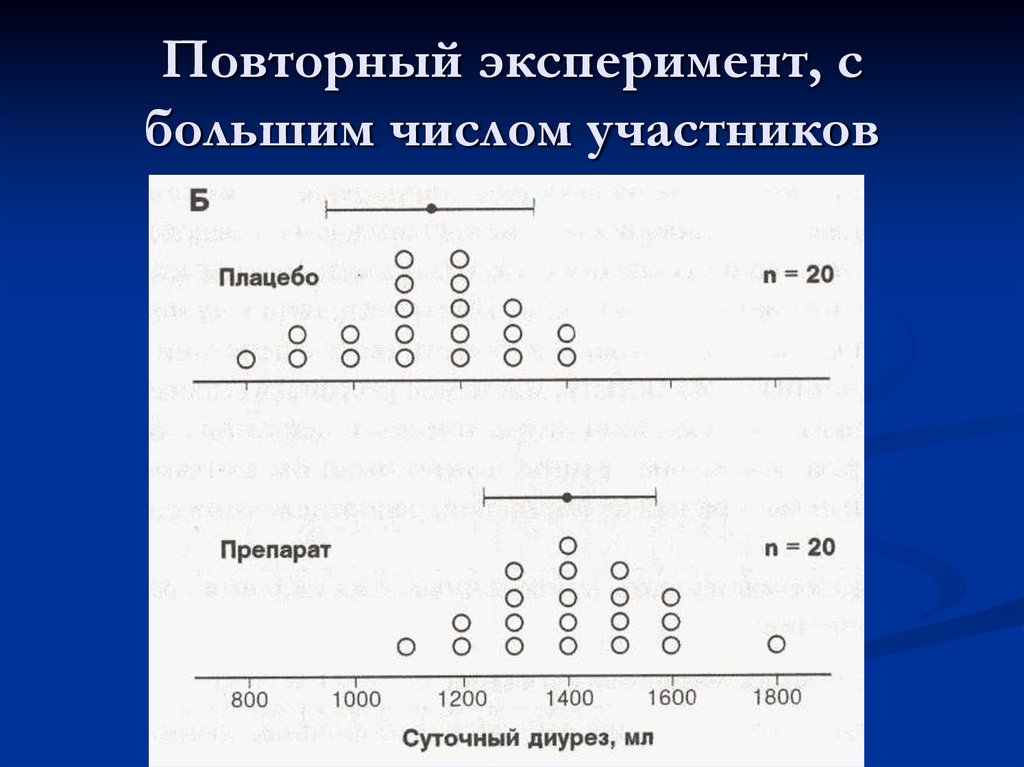
5. Повторный эксперимент, с большим числом участников
6. Точность выборочной средней оценивается с помощью стандартной ошибки
ssx
n
7.
Чем меньшестандартные ошибки средних
двух сравниваемых групп,
тем меньше и неопределенность
в оценке разности этих двух средних.
8. Критерий Стьюдента (t-критерий)
x1 x2t
sx1 x2
9. Стандартное отклонение разности двух чисел
10. Дисперсия разности двух случайно извлеченных значений
11. Стандартная ошибка разницы двух средних
sx1 x2 s s2
x1
2
x2
12. 6.2. Критическое значение t
13. Распределение 200 человек по величине диуреза (t = -0.2)
14. Еще одна пара выборок… (t = -2.2)
15. И еще одна пара выборок… (t = 0)
16. Распределение значений t, вычисленных по 200 парам выборок
-20
t-распределение
симметрично
относительно 0
2
17. В 10 случаях из 200 (т.е. в 5% всех случаев) t меньше -2.1 или больше +2.1
18. Распределение значений t при бесконечно большом числе испытаний
-20
2
19. t = -2.2: различия есть???
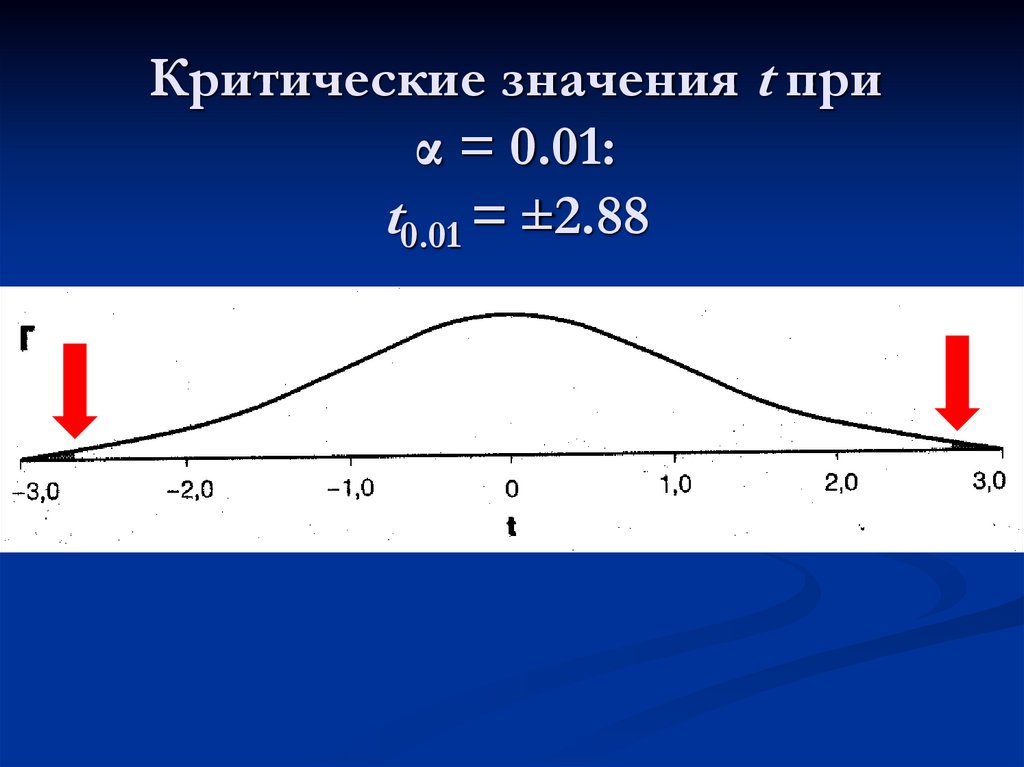
20. Критические значения t при α = 0.01: t0.01 = ±2.88
21. t = -2.2: различий нет!!!
22. Уровень значимости следует оговаривать до начала изложения результатов!
В разделе Материал и методы:... «различия считали статистически
значимыми при Р<0.01»
23. Чем определяется критическое значение t ?
Уровнем значимости:чем < α, тем > t
Числом степеней свободы:
df = n1 + n2 – 2
чем > n1 + n2 , тем <t
24. 6.3. Типичные ошибки в использовании критерия Стьюдента
25.
Критерий Стьюдентапредназначен исключительно
для сравнения ДВУХ групп!!!
26. Пример неправильного использования t-теста
ВЕЩЕСТВОВЕЩЕСТВО
ПЛАЦЕБО
А
В
С
Р1
Р2
Р3
27. Вероятность ошибиться хотя бы в одном из k сравнений при α = 0.05
Р′ = 0.05k28. Результаты исследования влияния гормонов человека на рост марсиан
29. Результаты исследования влияния гормонов человека на рост марсиан
t = 0.93t = 2.39
t0.05 = 2.101
t = 1.34
F = 2.74
F0.05 = 3.35
30.
Критерий Стьюдента являетсяпараметрическим критерием!
31. 6.4. Непараметрические методы сравнения двух выборок
32. Мы рассмотрим ранговые тесты:
U-тест Манна-Уитни (Mann-Whitney U-test);
Тест Уилкоксона (Wilcoxon
matched pairs test)
33. Пример подсчета суммы рангов в двух сравниваемых выборках
Выборка Ахi
Ранг
104
2
109
6
112
7
118
8
118
8
Сумма рангов =
31
Выборка В
хi
Ранг
100
1
105
3
107
4
107
4
108
5
Сумма рангов =
17
34. Данные Норм. распр., Ненорм. распр., дисп. одн. дисп. неодн. Зависимые Независимые Зависимые Независимые Парный t-тест t-тест
ДанныеНорм. распр.,
дисп. одн.
Зависимые
Независимые
Парный t-тест t-тест
Ненорм. распр.,
дисп. неодн.
Зависимые
Независимые
Тест Вилкоксона U-тест
35. 6.5. Методы множественных сравнений
36. Для чего разработаны методы множественных сравнений?
Дисперсионный анализпозволяет проверить гипотезу о
равенстве всех средних. Но если
гипотеза не подтверждается,
нельзя узнать, какая именно
группа отличается от других.
37. Post-hoc анализ (=апостериорный анализ):
Это группа методов, используемыхпосле дисперсионного анализа
для уточнения его результатов.
38. Поправка Бонферрони (Bonferroni correction):
α′ = α/kНапример, при k = 3, в каждом
из сравнений
α′ = 0.05/3 = 0.017 (1.7%)
Работает, если k невелико!
39. Критерий Ньюмена-Кейлса (Newman-Keuls test)
qx A xB
1
1
2 n A nB
S
2
вну
40. Другие методы множественных сравнений:
Критерий Тьюки (Tukey honestsignificant difference (HSD) test);
Критерий Шеффе (Scheffe test);
Критерий Даннета (Dunnet test)
41.
Результаты выполнениятеста Тьюки в программе
STATISTICA








































 mathematics
mathematics








