Проверка статистических гипотез. Сравнение двух математических ожиданий. Лекция 16

1.

Лекция 16
Проверка статистических
гипотез. Сравнение двух
математических ожиданий.
Аскарова А.Ж.

2. План лекции

1. Сравнение математических
ожиданий.
2. Проверка гипотез о равенстве
средних при известных
дисперсиях.
3. Примеры.
Аскарова А.Ж.

3. Сравнение математических ожиданий

Теорема (о распределении выборочных
характеристик).
Если генеральная совокупность Х распределена по
нормальному закону с параметрами a и , то:
1) случайная величина X в распределена нормально
с параметрами a,
n
nDв
2
2) 2 имеет распределение n 1 ;
3) случайные величины X и D независимы.
в
в
Аскарова А.Ж.

4. Сравнение математических ожиданий

Проверка гипотезы о равенстве математических
ожиданий двух генеральных совокупностей имеет
важное практическое значение. Действительно,
иногда оказывается, что средний результат хв
одной серии наблюдений отличается от среднего
результата у в другой серии.
Возникает вопрос: можно ли это различие
объяснить случайной ошибкой экспериментов или
оно неслучайно? Иначе говоря, можно ли считать, что
результаты экспериментов представляют собой
выборки из двух генеральных совокупностей с
одинаковыми средними.
Аскарова А.Ж.

5. Сравнение математических ожиданий

Пусть генеральные совокупности Х и Y
распределены по нормальному закону, причем их
средние квадратические отклонения известны и
равны соответственно x и y .
Требуется по двум независимым выборкам
х1 , х2 ,..., хn и y1, y2 ,..., ym из
генеральных совокупностей Х и Y проверить
гипотезу о равенстве генеральных средних
Основная гипотеза имеет вид: Н0: М(Х) = М(У)
Аскарова А.Ж.

6. Сравнение математических ожиданий

Построим критерий проверки этой гипотезы,
основываясь на следующем соображении: так как
приближенное представление о математическом
ожидании дает выборочная средняя, то в основе
проверки гипотезы
Н0: М(Х) = М(У)
(1)
должно лежать сравнение выборочных
средних X в , Y в .
Найдем закон распределения разности X в Y в .
Аскарова А.Ж.

7. Сравнение математических ожиданий

Разность
X Y
в
в
является случайной
величиной, и если гипотеза (1) верна, то
x1 ... xn y1 ... ym
M X в Yв М
M X M Y 0
n
m
Пользуясь свойствами дисперсии, получим
x1 ... xn y1 ... ym nD X mD Y x y
D X в Yв D
2
2
n
m
n
m
n
m
2
2
Аскарова А.Ж.
(2)

8. Сравнение математических ожиданий

Так как случайная величина X в Y в является
линейной комбинацией независимых нормально
распределенных случайных величин
Y1 , Y2 ,..., Ym , то X в Y в распределена по
нормальному закону с параметрами а 0,
2
2
х
n
y2
m
Аскарова А.Ж.

9. Сравнение математических ожиданий

В качестве критерия выберем пронормированную
случайную величину X в Y в , т.е.
K
X в Yв
x2
n
m
2
y
(3)
Таким образом, если (1) верна, то случайная
величина К имеет нормальное распределение
Аскарова А.Ж.

10. Сравнение математических ожиданий

Теперь зададимся уровнем значимости и
перейдем к построению критических областей и
проверке гипотезы (1)
1. Альтернативная гипотеза имеет вид
Н1: М(Х) > М(У)
(4)
В этом случае критическая область есть интервал
х ; , где Р(К>К )= α
пр
кр
Аскарова А.Ж.

11. Сравнение математических ожиданий

Подставляя в (3) числовые значения, найдем
значение критерия Кнаб.
Если
Кнаб>Ккр , то гипотезу Н0 (1)
отвергаем и принимаем гипотезу Н1 (4).
Поступая таким образом, можно допустить ошибку
первого рода с вероятностью .
Аскарова А.Ж.

12. Сравнение математических ожиданий

2. Альтернативная гипотеза имеет вид
Н1: М(Х) ≠ М(У)
(5)
В этом случае наибольшая мощность критерия
достигается при двусторонней критической
области, состоящей из двух интервалов
; хлев и хпр ; .
Критические точки определяются из условия
Р(К>|Ккр|)= α/2
Аскарова А.Ж.

13. Сравнение математических ожиданий

Если числовое значение критерия Кнаб ,
вычисленное по формуле (3) попадает в интервал
; хлев или в интервал хпр ; , то принимаем
гипотезу Н1.
Если
х лев К наб хпр , то принимаем гипотезу Н .
0
Аскарова А.Ж.

14. Сравнение математических ожиданий

Для проверки гипотезы, соответствие двух
выборок принадлежности к одной и той же
генеральной совокупности, рассмотрим вопрос о
значимости расхождений между выборочным
значением математических ожиданий. Выдвинем
нулевую гипотезу о равенстве математических
ожиданий. Н0: Мx =Мy
Аскарова А.Ж.

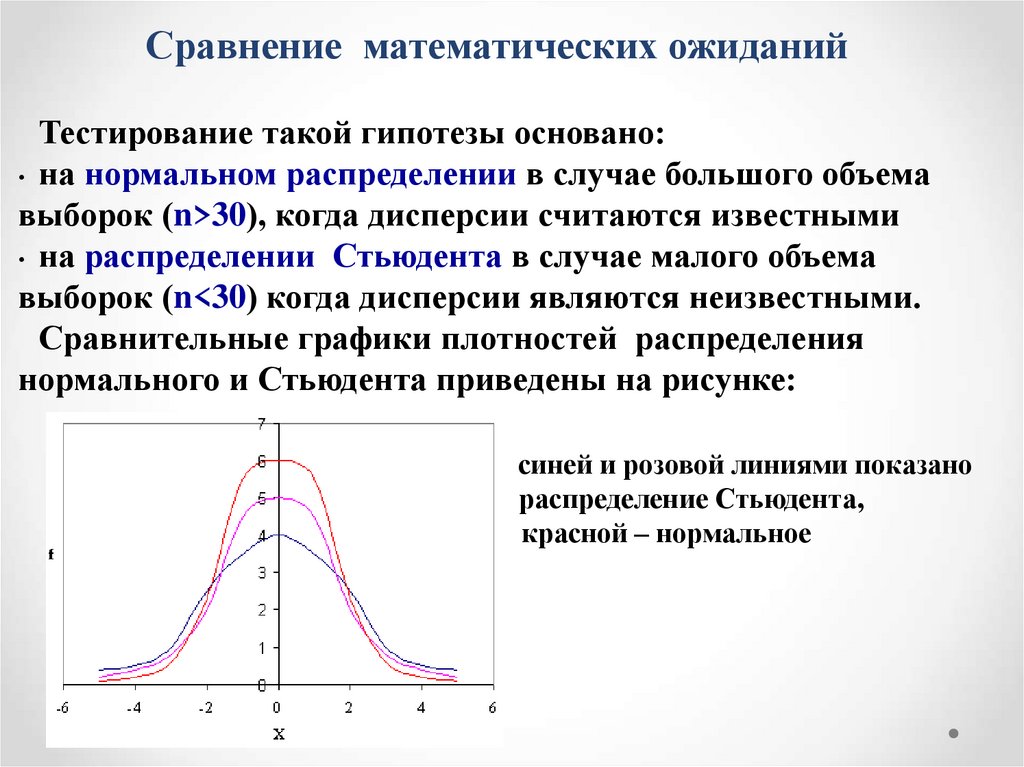
15. Сравнение математических ожиданий

Тестирование такой гипотезы основано:
• на нормальном распределении в случае большого объема
выборок (n>30), когда дисперсии считаются известными
• на распределении Стьюдента в случае малого объема
выборок (n<30) когда дисперсии являются неизвестными.
Сравнительные графики плотностей распределения
нормального и Стьюдента приведены на рисунке:
синей и розовой линиями показано
распределение Стьюдента,
красной – нормальное

16. Проверка гипотезы о равенстве средних при известных дисперсиях

Для того чтобы при заданном уровне значимости α =0.05
проверить нулевую гипотезу Н0: Мх=Му о равенстве
математических ожиданий двух больших нормальных
выборок с известными дисперсиями Dх и Dу,
необходимо:
Вычислить наблюдаемое значение критерия:
Z набл X Y
Dx D y
nx n y
Построить критическую область в зависимости от
конкурирующей гипотезы:

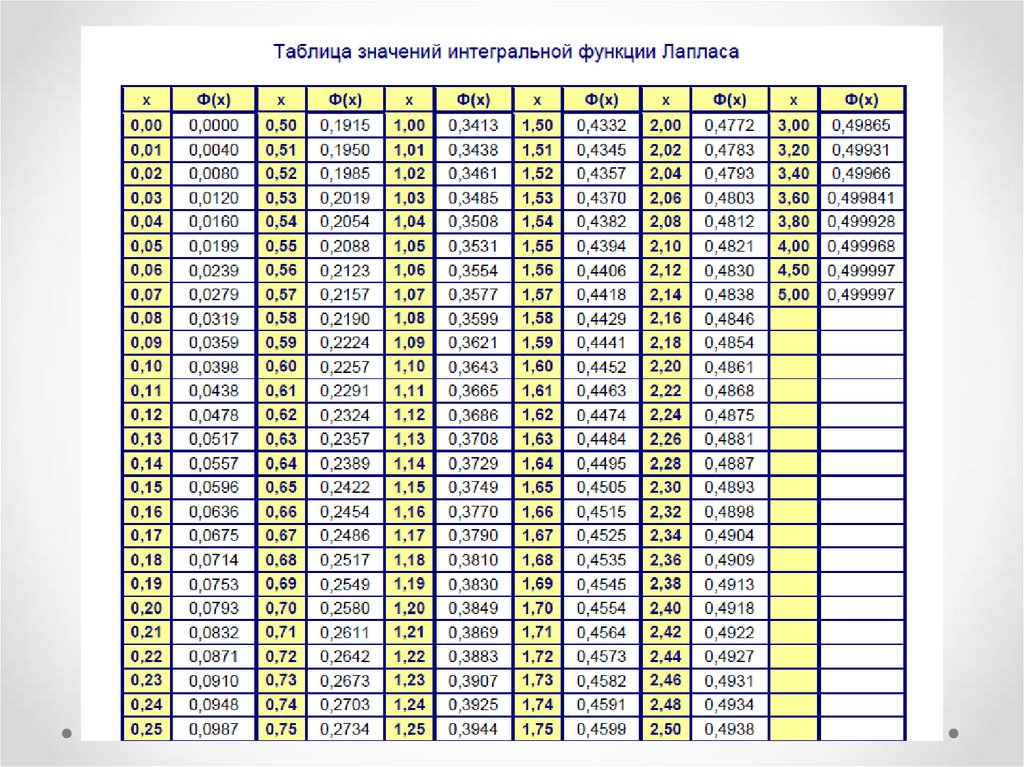
17. Проверка гипотезы о равенстве средних при известных дисперсиях

• при конкурирующей гипотезе Н1: Мх ≠ Му по таблице
функции Лапласа находят критическую точку zкр из
равенства Ф(zкр) = (1 – α) /2.
Если |Zнабл| < zкр, то нет оснований отвергать нулевую
гипотезу.
Если |Zнабл| > zкр, то нулевую гипотезу отвергают.
при конкурирующей гипотезе Н1: Мх > Му по таблице
функции Лапласа находят критическую точку zкр из
равенства Ф(zкр) = (1 – 2α) /2.
Если Zнабл < zкр, то нет оснований отвергать нулевую гипотезу.
Если Zнабл > zкр, то нулевую гипотезу отвергают.

18. Проверка гипотезы о равенстве средних при известных дисперсиях

при конкурирующей гипотезе Н1: Мх < Му по
таблице функции Лапласа находят
«вспомогательную критическую точку» zкр из
равенства Ф(zкр) = (1 – 2α) /2.
Если Zнабл > - zкр, то нет оснований отвергать
нулевую гипотезу.
Если Zнабл < - zкр, то нулевую гипотезу отвергают.

19. Пример 1

По двум независимым выборкам, извлеченным
из нормальных генеральных совокупностей,
объемы которых равны n = 12 и m = 8 , найдены
средние значения хв = 143 , у в = 122.
• Генеральные дисперсии известны: x2 D( X ) 36,
y2 D(Y ) 8. При уровне значимости α = 0.005
проверить гипотезу Н0 :M(X ) = M(Y) при
конкурирующей гипотезе M(X ) > M(Y) .
Аскарова А.Ж.

20. Решение

Критическую точку находим по таблице Лапласа
из условия Ф(zкр) = (1 – 2α) /2.
При уровне значимости α = 0.005 получаем
Ф(zкр) = (1 – 2α) /2= 0,495.
Получаем zкр = 2,58.
Наблюдаемое значение критерия
K наб
143 122 21
10,5
2
36 8
12 8
Так как 10,5>2,58, то гипотеза о равенстве
генеральных средних отвергается на уровне
значимости 0,005
Аскарова А.Ж.

21.

22.

23. Пример 2

По двум большим независимым выборкам объемов
nх = 40 и nY = 50 нормальных распределений найдены
выборочные значениями математических
ожиданий
x = 130 и у = 140.
Дисперсии известны DX = 80 и DY = 100.
При уровне значимости a = 0.01 проверить нулевую
гипотезу H0: mX = mY о равенстве математических
ожиданий при конкурирующей гипотезе H1: mX≠mY.

24. Решение

Найдем наблюдаемое значение критерия:
=
= - 5.
По условию конкурирующая гипотеза имеет вид
H1: mX≠ mY, поэтому критическая область – двусторонняя.
Найдем критическую точку zkp из равенства
Ф(zkp) = (1- a)/2 = (1 – 0.01)/2 = 0.495 .
По таблице функции Лапласа находим zkp = 2.58 .
Так как |Zнабл|= |-5|= 5 > zkp = 2.58, то нулевую гипотезу
отвергают. Другими словами, выборочными значениями
математических ожиданий различаются значимо.

25. Проверка гипотезы о равенстве средних при неизвестных дисперсиях

Постановка задач: пусть генеральные совокупности
распределены нормально, причем их дисперсии Dx и Dy
заранее не известны. Взяты две выборки малого объема,
требуется сравнить средние этих генеральных совокупностей.
Методика проверки задач: заключается в использовании
критерия Стьюдента при условии, что генеральные
дисперсии не известны, однако в предположении, что они
равны между собой.
Такая задача возникает: если сравниваются средние размеры
двух партий деталей, изготовленных на одном и том же
станке. Естественно будет предположить, что дисперсии
контролируемых размеров одинаковы.

26. Алгоритм проверки

1)Прежде чем сравнивать средние требуется проверить
Н0: Dх=Dу
2) Если гипотеза подтвердилась нужно вычислить
наблюдаемое значение критерия:
Тн
Х Y
x S x2 y S y2
nx n y (nx n y 2)
nx n y
3) Строим критическую область в зависимости от
конкурирующей гипотезы

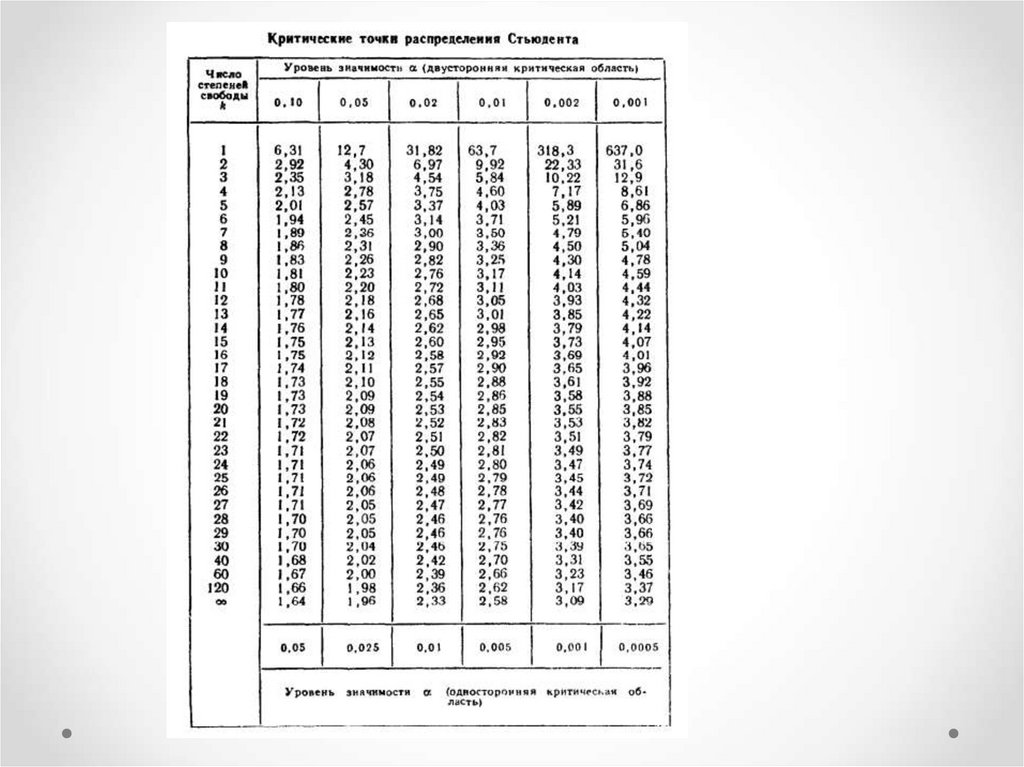
27. Алгоритм проверки

а) Если Н1: Мх ≠ Му – двусторонняя критическая область
строится исходя из условия чтобы вероятность попадания
наблюдаемого значения критерия в эту область была равна
принятому уровню значимости α взятого из таблицы
Стьюдента для числа степеней свободы в верхней части
таблицы, т.е. для двусторонней критической области при
условии |Тнабл| < tкр(α,υ), то нет основания отвергать нулевую
гипотезу; если |Тнабл| > tкр(α,υ), то нулевую гипотезу
отвергают.

28. Алгоритм проверки

б) Если Н1: Мх >Му строится правосторонняя
критическая область, а критическую точку находят
по таблице Стьюдента из нижней части.
Если Тнабл < tкр, то нет основания отвергать нулевую
гипотезу .
Если Тнабл > tкр, то нулевую гипотезу отвергают.

29. Алгоритм проверки

в) При конкурирующей гипотезе Н1: Мх < Му по таблице
критических точек распределения Стьюдента, по заданному
уровню значимости α,помещенному в нижней строке таблицы,
и числу степеней свободы k= nх + nу–2 найти
«вспомогательную критическую точку» tкр односторонней
критической области.
Если Тнабл < - tкр, то нет основания отвергать нулевую
гипотезу.
2
Если Тнабл > - tкр, то нулевую гипотезу отвергают.
2
2
S2
Т набл ( X Y )
2
y
S x2 S
nx n y
2
S x2 S y
( )
nx n y
Тнабл и число степеней свободы.
Sx y
nx n y
x
y

30. Пример 3

По двум малым независимым выборкам объемов nX = 5
и nY = 5 нормальных распределений найдены выборочные
значениями математических ожиданий
x = 13.32 и
у = 13.80 и исправленные выборочные дисперсии
S²x= 3.37 и S2y= 0.46 . При уровне значимости
a = 0.05 проверить нулевую гипотезу H0: mX = mY при
конкурирующей гипотезе H1: mX≠mY.
Аскарова А.Ж.

31. Решение

Исправленные выборочные дисперсии различны,
поэтому проверим предварительно гипотезу о равенстве
дисперсий, используя критерий Фишера.
Найдем отношение большей исправленной дисперсии к
меньшей
= 3.37/0.46 ≈ 7.33.
Дисперсия S²x значительно больше дисперсии S2y ,
поэтому в качестве конкурирующей гипотезы примем
гипотезу H1: DX > DY. В этом случае критическая область –
правосторонняя. По таблице критических точек
распределения Фишера, по уровню значимости a = 0.05 и
числам степеней свободы k1 = nX - 1 = 5 – 1 = 4 и
k2 = nY = 5 - 1 = 5 – 1 = 4 находим критическую точку:

32. Решение

Fkp(a, k1, k2) = Fkp(0.05, 4, 4) = 6.39.
Так как Fнабл = 7.33 > Fkp = 6.39, то гипотеза о равенстве
дисперсий отклоняется.
Вычислим наблюдаемое значение критерия Стьюдента:
≈ - 0.55 .
Число степеней свободы
=
≈5
Аскарова А.Ж.

33. Решение

По условию конкурирующая гипотеза имеет
вид H1: mX≠mY, поэтому критическая область –
двусторонняя.
По таблице критических точек распределения Стьюдента,
по уровню значимости a = 0.05, помещенному в верхней
строке таблицы, и числу степеней свободы
k= nX + nY - 2 = 5 + 5 – 2 = 8 находим критическую точку:
tkp(a, k) = tkp(0.05, 8) = 2.31.
Так как |Tнабл|= 0.55 < tkp = 2.31, то нет оснований отвергать
нулевую гипотезу о равенстве математических ожиданий.
Другими словами, математические ожидания различаются
незначимо.
Аскарова А.Ж.