Similar presentations:
Треугольники — они повсюду!
1.
Треугольники — они повсюду!Презентация Бородиной В. 9Б класс.
2.
Понятие треугольникаОтметим какие-нибудь три точки, не
лежащие на одной прямой, и соединим их
отрезками. Получим геометрическую
фигуру, которая называется
треугольником. Отмеченные три точки
называются вершинами, а отрезки –
сторонами треугольника.
Треугольник
3.
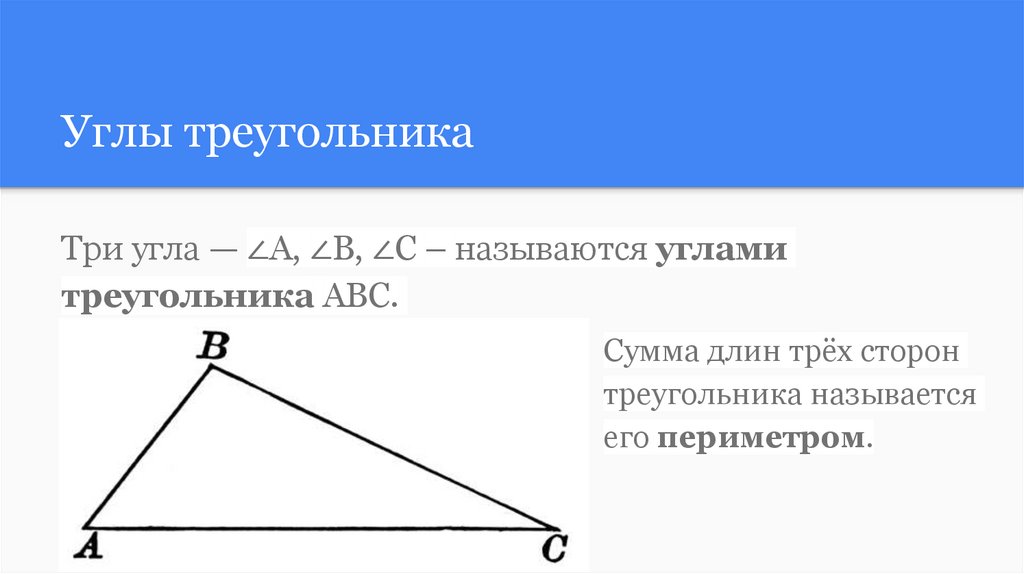
Углы треугольникаТри угла — ∠A, ∠B, ∠С – называются углами
треугольника ABC.
Сумма длин трёх сторон
треугольника называется
его периметром.
4.
Равные треугольникиЕсли два треугольника равны, то
элементы (т.е. стороны и углы)
одного треугольника
соответственно равны элементам
другого треугольника. В равных
треугольниках против соответственно
равных сторон лежат равные углы, и
обратно: против соответственно
равных углов лежат равные стороны.
5.
Первый признак равенства треугольникаКаждое утверждение, справедливость которого устанавливается путём рассуждений,
называется теоремой, а сами рассуждения называются доказательством теоремы.
Теорема:
Если две стороны и угол между ними одного треугольника соответственно
равны двум сторонам и углу между ними другого треугольника, то такие
треугольники равны.
Доказанная теорема выражает признак, по которому можно сделать вывод о равенстве
треугольников. Он называется первым признаком равенства треугольников.
6.
Перпендикуляр к прямойРассмотрим a и точку A, не лежащую на этой прямой.
Соединим точку A отрезком с точкой H прямой a. Отрезок AH
называется перпендикуляром, проведённым из точки A
к прямой a, если прямые AH и a перпендикулярны. Точка H
называется основанием перпендикуляра.
Теорема:
Из точки, не лежащей на прямой, можно провести
перпендикуляр к этой прямой, и притом только один.
7.
Медианы, биссектрисы и высотытреугольника
Отрезок, соединяющий вершину треугольника с серединой противоположной
стороны, называется медианой треугольника.
Отрезок биссектрисы угла треугольника, соединяющий вершину
треугольника с точкой противоположной стороны, называется
биссектрисой треугольника.
Перпендикуляр, проведённый из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
8.
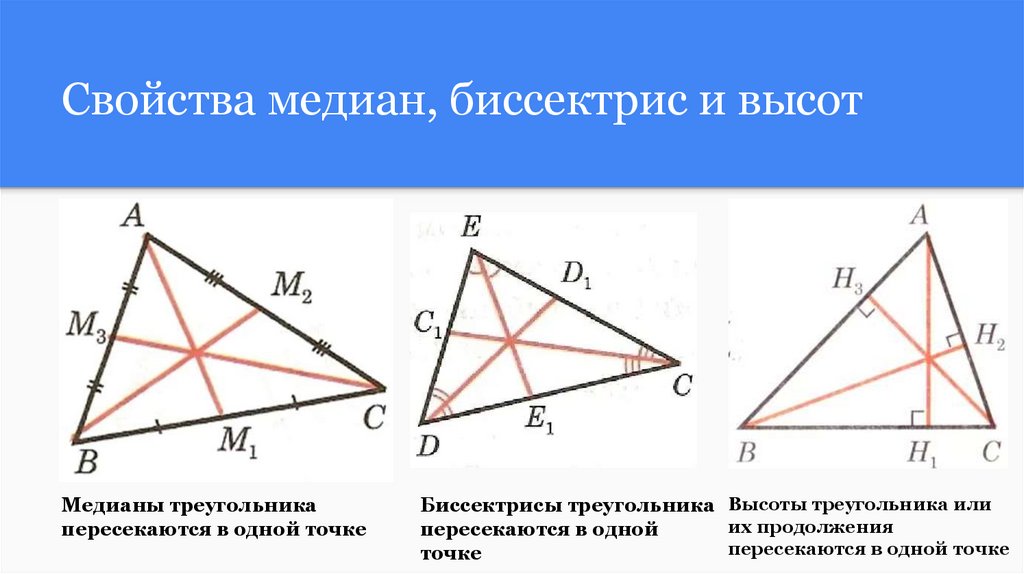
Свойства медиан, биссектрис и высотМедианы треугольника
пересекаются в одной точке
Биссектрисы треугольника Высоты треугольника или
их продолжения
пересекаются в одной
пересекаются в одной точке
точке
9.
Свойства равнобедренного треугольникаТреугольник называется
равнобедренным, если две его стороны
равны. Равные стороны называются
боковыми сторонами, а третья сторона –
основанием равнобедренного
треугольника.
Треугольник, все стороны которого равны,
называется равносторонним.
Теорема:
В равнобедренном треугольнике углы
при основании равны.
10.
Свойства равнобедренного треугольникаТеорема:
В равнобедренном треугольнике биссектриса, проведённая к
основанию, является медианой и высотой.








 mathematics
mathematics








