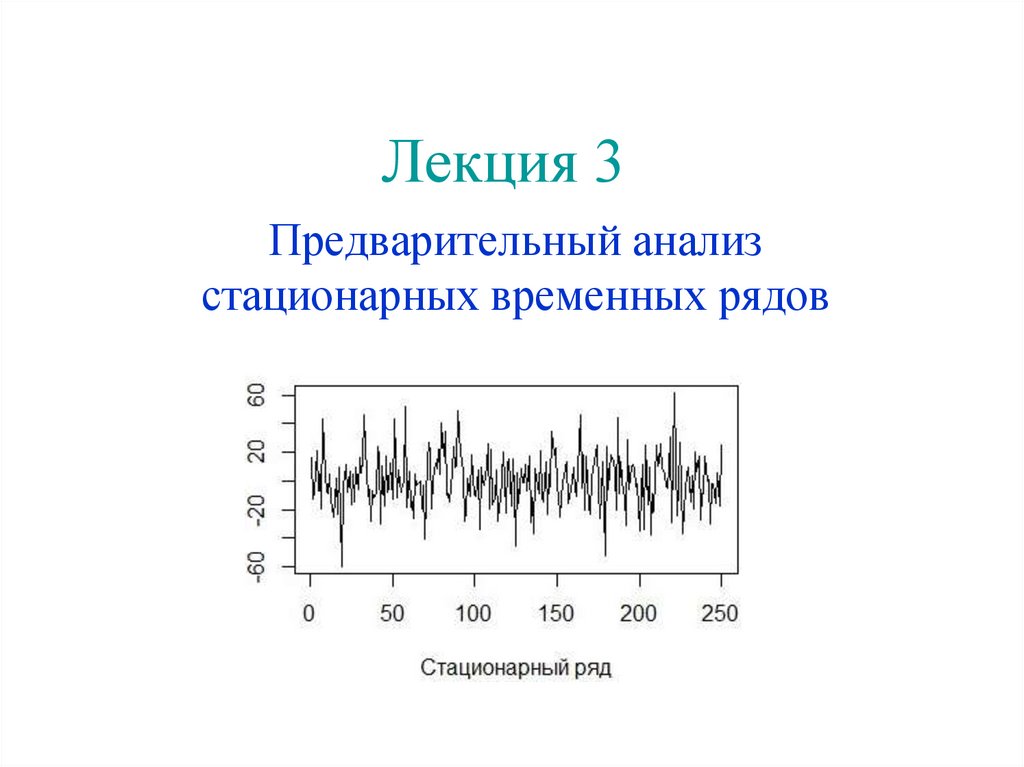
Предварительный анализ стационарных временных рядов. Лекция 3

1. Лекция 3

Предварительный анализ
стационарных временных рядов

2. План лекции

1. Этапы предварительного анализа стационарных
временных рядов
2. Компоненты временных рядов
3. Описательные характеристики стационарных
временных рядов
4. АКФ и ЧАКФ стационарных временных рядов
5. Параметрические критерии отсутствия тренда
6. Непараметрические критерии отсутствия тренда
7. Критерии проверки отсутствия сезонности
2

3. Реализуемые компетенции

ПК*-1 Способен переходить от содержательной постановки проблемы к математически
формализованному описанию, проводить исследования на основе построенной модели,
содержательно анализировать результаты; разрабатывать на их основе решения:
ПК*-1-В-2 Применяет математический инструментарий для описания социальных,
экологических, экономических процессов на макро и/или микро уровне в форме
математических моделей, их последующего исследования и выработки решений.
ПК*-5 Способен использовать знания современных языков программирования,
стандартных пакетов прикладных программ, информационно телекоммуникационной
сети "Интернет", инструментальных средств анализа данных при решении практических
задач управления информацией:
ПК*-5-В-3
Применяет
знания
стандартных
ППП,
информационно телекоммуникационных технологий, сети "Интернет" для поиска и
систематизации информации, анализа данных и моделирования, оформления
выполненных работ и представления их в виде презентаций, докладов
3

4. 1. Этапы предварительного анализа стационарных временных рядов

1.
2.
3.
4.
5.
Построение графика временного ряда
Проверка гипотезы об отсутствии тренда
Расчет описательных характеристик
Оценка АКФ и ЧАКФ
Проверка гипотезы об отсутствии
сезонности
4

5. 2. Компоненты временных рядов

Пусть рассматривается стационарный временной ряд 1, N 1 ,..., N
(ему соответствует y1, N у1 ,..., у N - апостериорный временной ряд). Далее в
зависимости от целей термин «временной ряд» будет использоваться и по
отношению к собственно случайной последовательности 1 ,..., N и к ее
реализации у1 ,..., у N .
Принято считать, что уровень временного ряда t , t 1,..., N можно
разложить на компоненты: тренд « f t », цикличность « сt », сезонность « vt »,
белый шум « t ».
5

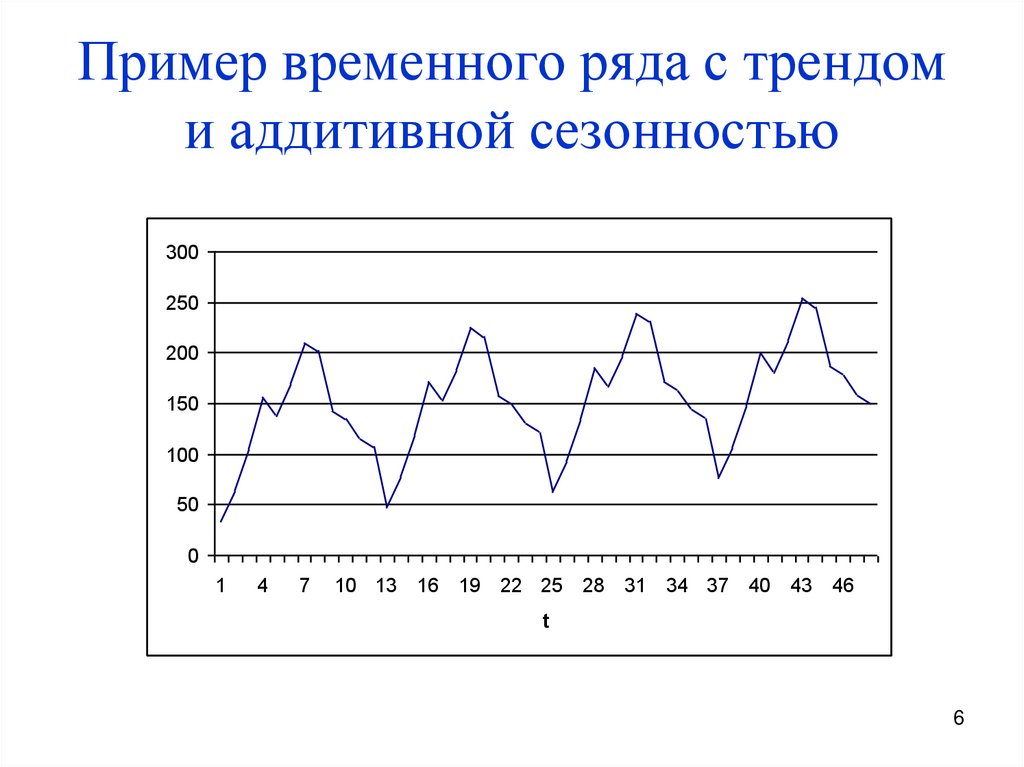
6. Пример временного ряда с трендом и аддитивной сезонностью

300
250
200
150
100
50
0
1
4
7
10 13 16 19 22 25 28 31 34 37 40 43 46
t
6

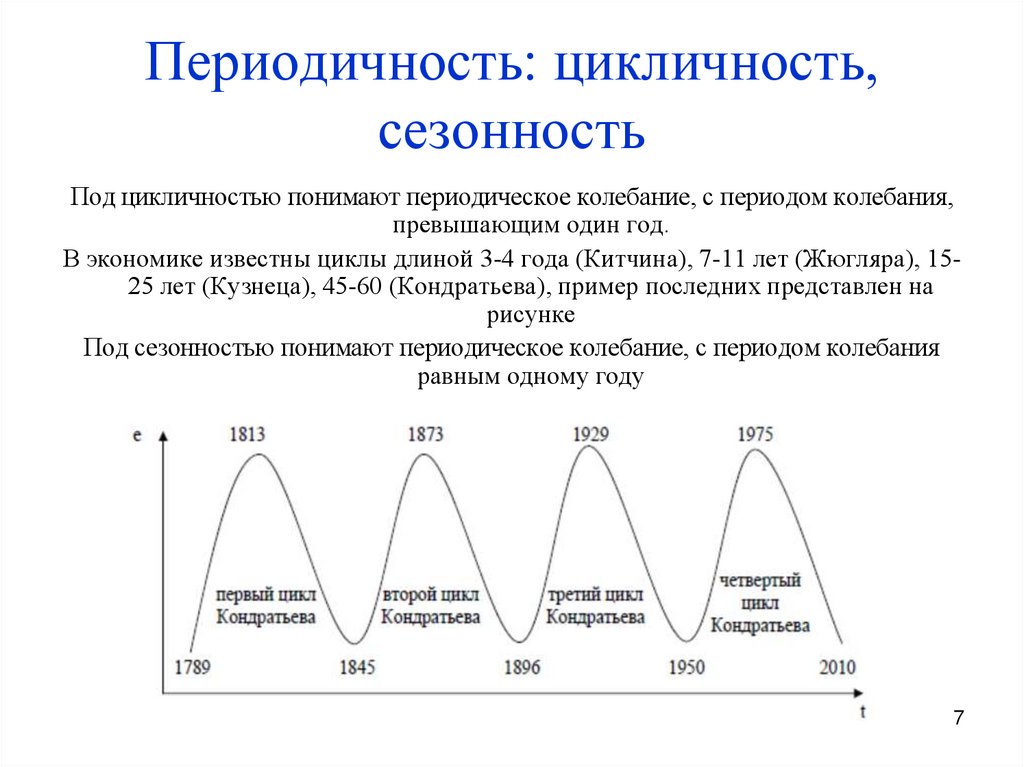
7. Периодичность: цикличность, сезонность

Под цикличностью понимают периодическое колебание, с периодом колебания,
превышающим один год.
В экономике известны циклы длиной 3-4 года (Китчина), 7-11 лет (Жюгляра), 1525 лет (Кузнеца), 45-60 (Кондратьева), пример последних представлен на
рисунке
Под сезонностью понимают периодическое колебание, с периодом колебания
равным одному году
7

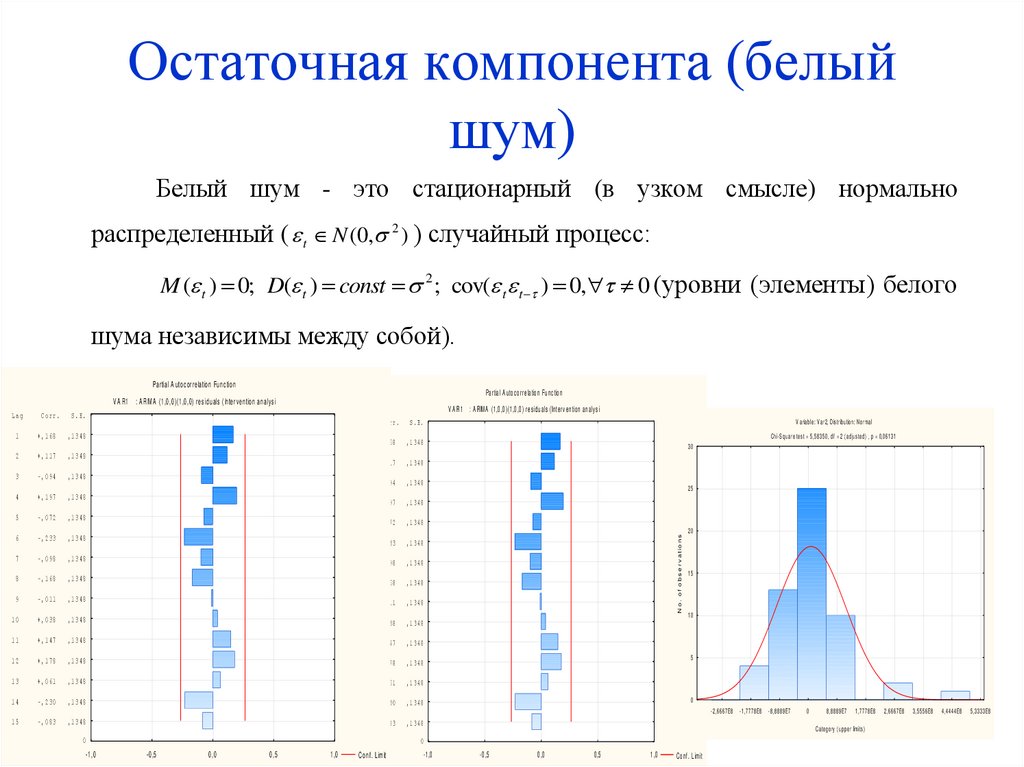
8. Остаточная компонента (белый шум)

Белый шум - это стационарный (в узком смысле) нормально
распределенный ( t N (0, 2 ) ) случайный процесс:
M ( t ) 0; D( t ) const 2 ; cov( t t ) 0, 0 (уровни (элементы) белого
шума независимы между собой).
Partial A utoc orrelation Func tion
Partial A utoc orrelation Func tion
V A R1 : A RIMA (1,0,0)(1,0,0) res iduals (Interv ention analy s i
Corr.
S.E.
1
+,168
,1348
2
+,117
,1348
3
-,094
,1348
4
+,197
,1348
5
-,072
,1348
6
-,233
,1348
7
-,098
,1348
8
-,168
,1348
9
-,011
10
Lag
Corr.
S.E.
1
+,168
,1348
2
+,117
,1348
3
-,094
,1348
4
+,197
,1348
5
-,072
,1348
6
-,233
,1348
7
-,098
,1348
8
-,168
,1348
,1348
9
-,011
,1348
+,038
,1348
10
+,038
,1348
11
+,147
,1348
11
+,147
,1348
12
+,178
,1348
12
+,178
,1348
13
+,061
,1348
13
+,061
,1348
14
-,230
,1348
14
-,230
,1348
15
-,083
,1348
15
-,083
,1348
V ariable: V ar2, Dis tribution: Normal
Chi-S quare tes t = 5,58350, df = 2 (adjus ted) , p = 0,06131
30
25
N o . o f o b s e r v a ti o n s
Lag
V A R1 : A RIMA (1,0,0)(1,0,0) res iduals (Interv ention analy s i
20
15
10
5
0
-2,6667E8
0
-1,0
0,0
0,5
1,0
Conf . Limit
-1,0
-8,8889E7
0
8,8889E7
1,7778E8
Category (upper limits )
0
-0,5
-1,7778E8
-0,5
0,0
0,5
1,0
Conf . Limit
2,6667E8
3,5556E8
4,4444E8
8
5,3333E8

9. Виды взаимодействия компонент временного ряда

Априорная модель временного ряда может быть представлена в виде
суммы (теоретически суммы всех компонент) соответствующих компонент
(аддитивный тип),
t f t ct vt t
(1)
в виде произведения (мультипликативный)
t f t * ct * vt * t
(2)
или может быть смешанного типа, например:
t f t * ct * vt t .
(3)
Модель стационарного временного ряда может быть представлена как:
t vt t .
(4)
9

10. 3. Описательные характеристики стационарных временных рядов

Для стационарных эргодических временных рядов рассчитываются
основные описательные характеристики, такие как оценка среднего, оценка
дисперсии, оценка моды, медианы и др.
Оценка среднего стационарного эргодического временного ряда
определяется по формуле:
N
yt
y t 1 ,
N
(5)
где y t - уровни временного ряда;
N – длина временного ряда (объем выборки).
Оценка дисперсии стационарных эргодических временных рядов имеет
вид:
N
( y y)
S t2 t 1
2
t
N
.
(6)
10

11. 4. Выборочные автокорреляционная и частная автокорреляционная функции стационарных эргодических временных рядов

По
реализации
случайной
выборки
найдена
оценка
среднего
временного ряда y . Тогда оценка R̂ ( ) r( ) - значение выборочной
автокорреляции порядка , которая определяется формулой:
N
y t y y t y
r̂ ( ) t 1 N
,
(7)
( y t y) 2
t 1
11

12. Выборочные автокорреляционная и частная автокорреляционная функции стационарных эргодических временных рядов

Оценка
частного
коэффициента
автокорреляции
порядка
стационарного временного ряда определяется по формуле:
Rˆ1,1
rˆчастн ( )
Rˆ Rˆ
,
(8)
11 1 ,1
где Rˆ i ,i - алгебраические дополнения матрицы R̂ :
r̂ 1
1
1
r̂ 1
R̂
...
...
r̂ r̂ 1
... r̂
... r̂ 1
...
... ,
...
1
(9)
______
где r̂ ( j ) – оценка коэффициента автокорреляции j-го порядка, j 1, .
12

13. Оценки АКФ и ЧАКФ ряда динамики авиаперевозок пассажиров

13

14. Оценки АКФ и ЧАКФ ряда первых разностей динамики авиаперевозок пассажиров

14

15. 5. Параметрические тесты проверки гипотезы об отсутствии тренда

• Отсутствие тренда сренднего: критерий
Стьюдента, критерий Фишера
(использование средней оценки дисперсии
по подпериодам), Критерий Аббе-Линника,
Кокса-Стюарта
• Отсутствие тренда дисперсии: критерий
Фишера (отношение оценок дисперсий),
критерий Кокрена, критерий Бартлетта
15

16. Критерий Стьюдента проверки гипотезы об отсутствии тренда среднего

Временной ряд y1, N длиной N разбивается на две части, не обязательно
одинаковые по количеству содержащихся в них значений, с количеством
наблюдений N1 ( t 1,2,...N1 ) и N 2 ( t N1 1,...N) соответственно.
Выдвигается нулевая гипотеза:
Н 0 : М 1,i М 2, j , i 1,..., N1, j N1 1,..., N
(постоянство
математического ожидания или отсутствие тренда среднего)
Н1 : i, j : М 1,i М 1, j
16

17. Критерий Стьюдента проверки гипотезы об отсутствии тренда среднего

Для каждой из частей определяются оценки y1 и S 12 , y 2 и S 22 - среднего и
дисперсии соответственно
а) дисперсии на участках не равны между собой. Если
нулевая
гипотеза верна, то статистика:
t( 1, N )
y( 1, N1 ) y( 2 ,N2 )
S
2
( 1, N1 )
N1
(значение статистики
tнабл t( у1,N )
S
2
( 2 , N 2 )
N (0,1)
(10)
N2
y1 y2
S12 S22 .
N1 N 2
17

18. Критерий Стьюдента проверки гипотезы об отсутствии тренда среднего

Дисперсии на участках равны между собой 12 22 2 .
Статистика находится по формуле
t( 1, N )
(t
y1 y2
S
y( 1, N1 ) y( 1, N1 )
S ( 1, N )
N1 N 2
St ( N1 N 2 2) ,
N1 N 2
(11)
N1 N 2
)
N1 N 2
18

19. Критерий Фишера (отношение дисперсий)

Предварительно производят разбиение исходного временного ряда на 2
части.
Н0 : 1 2
Н1 : 1 2
Статистика критерия Фишера определяется по следующей формуле:
F( 1, N )
max( S12( 1, N ) ; S 22( 1, N ) )
min( S12( 1, N ) ; S 22( 1, N ) )
F ( ; 1 ; 2 ) ,
(12)
где S12 и S 22 - несмещенные оценки дисперсии временного ряда на первой и
второй
частях
соответственно
с
числом
измерений
и
N1
N 2 . 1 N1 1 2 N 2 1 .
19

20. Критерий Кокрена

применяется в предположении, что объемы этих частей равны между
собой, т.е. N1 N 2 ...N n n .
Н 0 : 1 ... n
Н 1 : 1 ... n
Статистика критерия определяется по следующей формуле:
2
/( S12 S 22 ... S n2 ) ), (13)
K S 2max /( S 21 S 22 ... S 2n ) ( K набл S max
2
max ( S k2 ) j 1,2...n
где S max
j
20

21. Критерий Кокрена

Критическое значение находят выражая его через табличное значение,
найденное по распределению Фишера-Снедекора по формуле:
K крит
где
Fkp F 1 (1
Fкр
(n 1) Fкр
,
(14)
, 1 , 2 ) для заданного уровня значимости , числа степеней
n
свободы 1 n 1, 2 (n 1) 1 . Если K наб K крит , то нулевая гипотеза
отвергается, в противном случае принимается.
21

22. 6. Непараметрические тесты проверки гипотезы об отсутствии тренда

• Проверка отсутствия тренда среднего: Тест МаннаУитни, критерий Вальда-Вольфовитца, критерий
Шахнесси, Критерий серий, основанный на медиане
выборки, Критерий «восходящих» и «нисходящих»
серий, Критерий Фостера-Стюарта, критерий,
основанный на ранговой корреляции, критерий
Бартелса, Критерий Рамачандрана-Ранганатана,
критерий случайности Олмстеда, критерий инверсий,
Критерий кумулятивной суммы, знаково-ранговый
критерий Холина.
• Проверка отсутствия тренда дисперсии: критерий
Сиджела-Тьюки, Критерий Фостера-Стюарта
22

23. Тест Сиджела-Тьюки

Выдвигается нулевая гипотеза об отсутствии тренда среднего в ряду
динамики:
Н 0 : М 1,i М 2, j , i 1,..., N1, j N1 1,..., N
Н1 : i, j : М 1,i М 1, j
Алгоритм проверки по критерию Сиджела – Тьюки:
1.
Исходный временной ряд уt, t=1, 2, …, N центрируется.
2.
Временной ряд длиной N делится на две части (желательно
равные), так что на первой из них располагаются элементы первой
центрированной совокупности у1, а на второй – элементы совокупности – у2.
23

24. Тест Сиджела-Тьюки

3. Элементы из двух центрированных совокупностей у1 и у2
объединяются
в
одной
таблице
с
запоминанием
«своей
совокупности» согласно следующему правилу ранжирования. Ранг 1
приписывается наименьшему отрицательному значению, которое
располагается
на
первом
месте
вверху
таблицы.
Ранг
2
приписывается наибольшему положительному значению, которое
располагается на последнем месте в низу таблицы. Ранг 3
присваивается значению, следующему за наименьшим, которое
располагается на втором месте в верху таблицы. Ранг 4 – значению,
следующему за наибольшим, которое располагается в таблице на
втором месте снизу. Ранг 5 приписывается третьему по порядку
наименьшему значению. Оно располагается в таблице на третьем
месте сверху. Ранг 6 третьему по порядку наибольшему значению,
которое располагается на третьем месте таблицы снизу и т.д.
24

25. Тест Сиджела-Тьюки

4. Строится статистика z:
z ( 1, N )
где
N1+N2
–
R1
–
сумма
количество
R1
рангов
элементов
N1 ( N1 N 2 1) 1
2
2 N (0,1) ,
N1 ( N1 N 2 1)
12
элементов
первой
в
и
первой
(15)
совокупности
второй
у 1,
совокупности
соответственно.
25

26. Критерий Фостера-Стюарта

Критерий одновременно проверяет отсутствие тренда среднего и
дисперсии. Каждый уровень ряда сравнивается со всеми предшествующими.
При этом определяются вспомогательные характеристики:
1, у у t 1 , у t 2 ,..., у1
mt t
0,иначе
и
1, у уt 1 , уt 2 ,..., у1
lt t
0,иначе
Вычисляется величина разности d t mt lt , t 2, N и величина
N
N
t 2
t 2
st mt lt , t 2, N . Далее рассчитываются величины d d t и S S t .
26

27. Критерий Фостера-Стюарта

Показатель S применяется для обнаружения тенденции в дисперсиях,
d- для обнаружения тенденции в средней. Для проверки нулевой гипотезы
используют статистику:
t
D
f
(16)
или
t=
S 1, N f 2
L
S f2
),
St ( N 1) ( t набл
L
(17)
где L 2 ln N 3,4253 , f 2 ln N 0,8456 .
Формулы для f и L применимы при N>50
27

28. Критерий, основанный на ранговой корреляции

Выдвигается нулевая гипотеза об отсутствии тренда:
Н0: 0
Н1 0
Рассчитывается коэффициент ранговой корреляции Спирмэна:
6Q
,
3
N N
(18)
Q ( X t t) 2 .
(19)
ˆ 1
где X t - ранг y t ,
N
t 1
Для проверки гипотезы используется статистика:
t ( 1,n )
x , ( 1,n )
2
1 x , ( 1,n )
N 2 St ( N 2) ,
(20)
28

29. Критерий серий, основанный на медиане выборки

______
H0: M( t )=const, t 1, N
H1: M( t ) const
Этапы реализации данного метода:
1.
Серии «+» и «-» формируются при сравнении значений
исходного ряда с медианным значением.
2.
Определяется
длина наибольшей серии k max N и число
серий V N .
3.
Рассматриваются неравенства:
k max N 3,3 lg( N 1)
.
V
N
0
,
5
N
1
1
,
96
N
1
(21)
Если хотя бы одно из неравенств нарушено, то гипотеза об отсутствии
тренда отвергается.
29

30. Критерий «восходящих» и «нисходящих» серий

______
H0: M( t )=const, t 1, N
H1: M( t ) const
Критерий «восходящих» и «нисходящих» серий реализуется в виде
следующей последовательности шагов:
- Определяется последовательность знаков исходя из следующих
условий:
" " , уt уt 1 0
i
" " , уt уt 1 0
(22)
- подсчитывается N - число серий в совокупности i ,
где под серией понимается подряд идущие «+» или «-»
- определяется продолжительность самой длинной серии max ( N ) :
30

31. Критерий «восходящих» и «нисходящих» серий

проверка гипотез основана на том, что при условии случайности ряда
протяженность самой длинной серии не должна быть слишком большой, а
общее число серий не должно быть слишком маленьким.
1
16 N 29
]
( N ) [ (2 N 1) 1,96
,
3
90
( N ) ( N )
0
max
(23)
где 0 ( N ) находится по таблице:
N
<26
26-153
153-170
0 (N )
5
6
7
Если не выполняется одно из условий системы (23), следовательно, Н0
отвергается, то есть существует трендовая составляющая.
31

32. 7. Тестирование сезонности стационарных временных рядов

• Построение графика (лишь предположение)
• Анализ выборочных АКФ и ЧАКФ
позволяют сделать лишь предположение о
наличии сезонности
• Применение специальных критериев
32

33. Критерий «пиков и ям» проверки гипотезы об отсутствии периодичности

Н0: отсутствие сезонности
Н1: наличие сезонности
Условимся говорить, что в точке к временной ряд имеет пик, если
одновременно уk-1<уk, уk+1<уk и имеет яму, если значение уk меньше обеих
соседних. Будем говорить, что в точке к – экстремальная точка ряда, если в
этой точке пик или яма. Если в ряду попадается несколько равных значений,
причем все они больше (или, соответственно, меньше) их окружающих, то все
эти точки воспринимаются как одна экстремальная точка
Число экстремальных точек, обозначается через e .
Для проверки нулевой гипотезы строится t- статистика:
t ( 1,N )
3e - 2N 4
10 N (0,1) .
16 N 29
(24)
33

34. Сведение задачи проверки наличия периодичности к задаче дисперсионного анализа

Пусть, например, рассматривается аддитивная модель временного ряда
t f t vt t ,
(25)
где t=1,2,…,N.
Период сезонной составляющей известен и равен m. Тогда исходный
временной ряд можно представить в виде матрицы Y с элементами:
y ij fˆij vˆij zij ,
(26)
где i=1,2,…,n; j=1,2,…,m,
n*m=N, то есть n – число полных фаз сезонной волны.
34

35. Сведение задачи проверки наличия периодичности к задаче дисперсионного анализа

Запишем эту матрицу:
Год
Месяц/квартал
j=1 j=2 j=3 … j=m-1 j=m
i=1
y11
y12
y13 …
y 1m-1
y1m
i=2
y 21
y 22
y 23 …
y 2m-1
y 2m
…
…
…
… …
…
..
i=n
y n1
y n2
y n3 …
y nm-1
y nm
Для выяснения влияния фактора сезонности на уровни временного ряда
применим однофакторный дисперсионный анализ
35

36. Сведение задачи проверки наличия периодичности к задаче дисперсионного анализа

Н 0 : v1 ... vm (нет влияния сезонности)
Н 1 : i, j : vi v j (есть влияние сезонности)
Критерий Краскала-Уоллиса
Для реализации критерия необходимо от ряда y t перейти к ряду рангов
R t которые записываются в таблицу аналогичной размерности:
Год
Сезон
j=1
j=2
… j=m
i=1
R 11
R 12
…
R 1m
i=2
R 21 R 22
…
R 2m
…
…
…
….
..
i=n
R n1 R n2
…
R nm
36

37. Сведение задачи проверки наличия периодичности к задаче дисперсионного анализа

Рассчитываются средние ранги по каждому столбцу (сезону):
1 n
R * j R ij .
n i 1
(27)
Если влияния сезонного фактора нет, то средние ранги будут мало
отличаться от среднего ранга по всему временному ряду:
R
N 1
.
2
(28)
Строится статистика:
m
12
2
n j R* j R 2 (m 1) .
W( 1, N )
N ( N 1) j 1
(29)
37

38. Литература к лекции

1.
2.
3.
4.
Кобзарь А.И. Прикладная математическая статистика.
Для инженеров и научных работников. – М.:
ФИЗМАТЛИТ, 2006. – 816 с.
Струнов В.И.. О применении критерия Аббе для анализа
независимости рядов измерений, характеризующихся
отличными от нормального законами распределения //
Измерительная техника. 2006. № 8. – С. 13-17.
Тихомиров, Н.П. Эконометрика [Текст] : учеб. для
вузов / Н.П. Тихомиров, Е.Ю. Дорохина; Рос. Эконом.
Акад. им. Г.В. Плеханова. -М. : Экзамен, 2003. - 512 с.
Химмельблау, Д. Анализ процессов статистическими
методами. / Д. Химмельблау. – М.: Мир, 1973. – 957
38