Similar presentations:
Временные ряды в эконометрических исследованиях
1. Временные ряды в эконометрических исследованиях
1.Специфика временного ряда как источника данных в
эконометрическом моделировании
2. Автокорреляция уровней ряда и ее последствия
3. Моделирование тенденций временного ряда
4. Использование трендовых моделей для прогнозирования
5. Моделирование периодических колебаний
6. Моделирование взаимосвязей по временным рядам. Методы
исключения тенденции
7. Автокорреляция в остатках. Критерий Дарбина-Уотсона
8. Обобщенный метод наименьших квадратов при построении модели
регрессии по временным рядам
9. Сезонные колебания их учет при построении эконометрических
моделей
10. Модели с лаговыми переменными. Метод инструментальных
переменных. Метод Алмон
2. Модели на основе рядов динамики
• Модели изолированного динамического ряда• Модели системы взаимосвязанных рядов
динамики
• Модели автрегрессии
• Модели с распределенным лагом
3. Компоненты временного ряда
• Тенденция (T)• Периодические колебания (P)
• Случайные колебания (E)
yt f (T , P, E )
4. Ряд без тенденции и периодических колебаний (стационарный ряд)
yt y E5. Ряд с тенденцией
y1
2
3
4
5
6
7
8
9
10
yt f (T ) E
t
6. Ряды с периодическими колебаниями
yy
20
20
5
5
1
2
t
1
Ряд с периодическими и случайными
колебаниями
y t f ( P, E )
2
t
Ряд с тенденцией, периодическими и
случайными колебаниями
yt f (T , P, E)
7.
Аддитивнаямодель
Мультипликативная
yt T P E
yt T P E
yо
yо
10
5
10
5
1
2
t
модель
1
2
t
8. Автокорреляция уровней ряда
Корреляционная зависимость междупоследовательными значениями уровней
временного ряда называется автокорреляцией
уровней ряда
ryt yt 1
yt yt 1 yt yt 1
y y
t
t 1
9. Пример
Имеются данные о расходах на конечноепотребление и уровне дохода за 7 промежутков
времени в д.е. yt - расходы на потребление, xtдоходы
t
1
2
3
4
5
6
7
yt
7
8
10
9
11
12
14
12
13
16
15
16
18
19
xt
10.
txt 1
xt
1
12
-
2
3
4
5
6
7
Итого
13
16
15
16
18
19
Х
12
13
16
15
16
18
Х
rxt xt 1 0,81
yt
yt 1
7
8
10
9
11
12
14
Х
-
7
8
10
9
11
12
X
ryt yt 1 0,84
11. Этапы построения модели тенденции (уравнения тренда)
• Выбор математической функции, описывающейтенденцию
• Оценка параметров модели
• Проверка адекватности выбранной функции и оценка
точности модели
• Расчет точечного и интервального прогнозов
12. Виды математических функций, описывающих тенденцию
• Функции с монотонным характером возрастания(убывания) и отсутствием пределов роста (снижения)
• Кривые с насыщением, т. е. устанавливается нижняя или
верхняя граница изменения уровней ряда
• S-образные кривые, т. е. кривые с насыщением, имеющие
точку перегиба
13. Уравнения трендов
линейная: y a bt2
y
a
bt
ct
параболическая:
b
степенная: y at
b
y
a
гипербола:
t
t
y
a
b
показательная:
a bt
y
e
экспонента:
14. Линейный тренд
yt a btt
yt a bt yt yt yt 1
1
a b
2
a 2b
3
a 3b
b
b
4
a 4b
b
-
15. Парабола 2-го порядка
yt a bt ct2
t
yt a bt ct 2
Скорость
Ускорение
yt yt yt 1
t t t 1
1
a b с
-
-
2
a 2b 4с
b 3с
-
3
a 3b 9c
b 5с
2c
4
a 4b 16c
b 7с
2c
16. Показательная функция
yt a bt
t
yt a bt
K yt yt 1
1
ab
-
2
ab 2
b
3
ab3
b
4
ab 4
b
17. Степенной тренд
y attb
K n 1 t b
период
b
- базисный коэффициент роста
- средний коэффициент роста за
18. Использование трендовых моделей для прогнозирования
Se( yˆ p )1 t p t 2
MS E 1
2
n t t
yˆ p ttab. Se yˆ p Yˆp yˆ p ttab. Se yˆ p
19. Методы исключения тенденции при моделировании взаимосвязей по временным рядам
• Метод отклонений от тренда• Метод последовательных разностей
• Включение в модель регрессии по временным
рядам фактора времени
20. Метод отклонений от тренда
eyt yt yˆtext xt xˆt
eyt a b ext
21.
( yt yˆt ) b( xt xˆt )yt yˆt b( xt xˆt )
y p yˆt p b( x p xˆt p )
22.
yp- прогнозное значение уt
yˆ t p - прогноз у по тренду при t=p
xp
xˆt p
- прогнозное значение хt
- прогноз хt исходя из уравнения
тренда при t=p
23. Метод последовательных разностей
yt yt yt 1xt xt xt 1
yt a b xt
24.
( yt yt 1 ) a b( xt xt 1 )yt yt 1 a b( xt xt 1 )
y p y n a b( x p xn )
25.
y p - прогнозное значение уровня ряда yt
yn
- конечный уровень динамического ряда
x p и x n - то же по ряду
xt
yt
26. Включение в модель регрессии по временным рядам фактора времени
yt a bxt ctP aK L e
b1
b2
ct
ln P ln a b1 ln K b2 ln L ct
27. Пример Исключение тенденции методом отклонений от тренда
t1
2
3
4
5
6
7
Xt
12
13
16
15
16
18
19
Доходы
Доходы
(усл.де
н.ед.)
x = 1,1071t + 11,143
R2 = 0,91
20
18
16
14
12
10
8
6
4
2
0
Ряд1
Линейная (Ряд1)
1
2
3
4
5
Годы
6
7
y= 1,0714t + 5,8571
R2 = 0,9221
16
14
12
10
8
6
4
2
0
Расходы на потребление
Годы
Расход
ы на
потреб
ление
товара
(усл.де
н.ед.)
yt
7
8
10
9
11
12
14
Ряд1
Линейная (Ряд1)
1
2
3
4
5
Годы
6
7
28.
tyt
Xt
ey
ex
1
7
12
0,071429
-0,25
2
8
13
0
-0,35714
3
10
16
0,928571
1,535714
4
9
15
-1,14286
-0,57143
5
11
16
-0,21429
-0,67857
6
12
18
-0,28571
0,214286
7
14
19
0,642857
0,107143
29.
ВЫВОД ИТОГОВРегрессионная статистика
Множественный
0,729664
R
R-квадрат 0,53241
Нормированный
0,438892
R-квадрат
Стандартная 0,50382
ошибка
Наблюдения
7
Дисперсионный анализ
df
SS
MS
F
Регрессия
1 1,445113 1,445113 5,693128
Остаток
5 1,269173 0,253835
Итого
6 2,714286
Коэффициенты
Стандартнаяt-статистика
ошибка
Нижние 95%
Верхние 95%
Y-пересечение
4,69E-16 0,190426 2,46E-15 -0,48951 0,489506
ex
0,652632 0,273522 2,386028 -0,05048 1,355743
eˆ
y
t
0 , 652
e
xt
30. Пример Исключение тенденции методом первых разностей
Расходына
потребле
ние
товара
(усл.ден.е
д.)
Годы
t
yt
1
2
3
4
5
6
7
Доходы
(усл.ден.ед.)
Xt
7
8
10
9
11
12
14
∆y t
12
13
16
15
16
18
19
∆Xt
1
2
-1
2
1
2
1
3
-1
1
2
1
Регрессионная статистика
Множественный R 0,750824
R-квадрат
∆y=0,39+0,66∆x
0,563737
Дисперсионный анализ
df
Регрессия
Остаток
Итого
1
4
5
SS
3,852201258
2,981132075
6,833333333
Коэффициенты
Стандартная ошибка
Y-пересечение
0,396226
0,48893051
Переменная X 1
0,660377
0,290468006
MS
F
3,852201258 5,168776
0,745283019
t-статистика
0,810394129
2,273494309
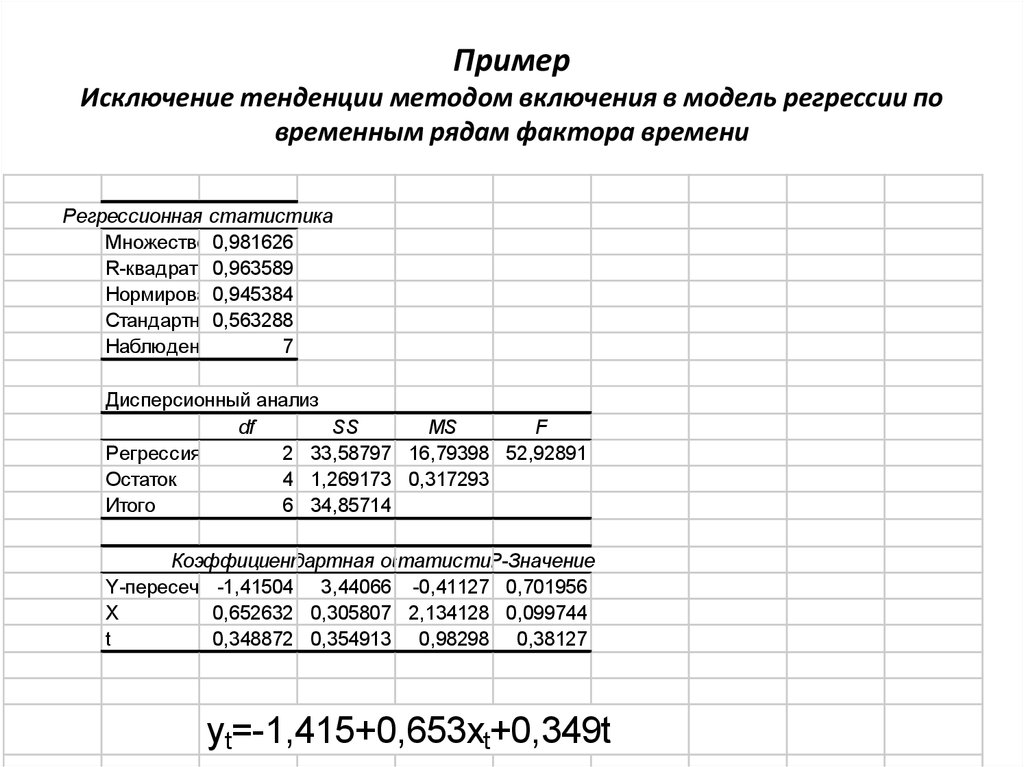
31. Пример Исключение тенденции методом включения в модель регрессии по временным рядам фактора времени
Регрессионная статистикаМножественный
0,981626
R
R-квадрат 0,963589
Нормированный
0,945384
R-квадрат
Стандартная0,563288
ошибка
Наблюдения
7
Дисперсионный анализ
df
SS
MS
F
Регрессия
2 33,58797 16,79398 52,92891
Остаток
4 1,269173 0,317293
Итого
6 34,85714
Коэффициенты
Стандартнаяt-статистика
ошибка
P-Значение
Y-пересечение
-1,41504 3,44066 -0,41127 0,701956
X
0,652632 0,305807 2,134128 0,099744
t
0,348872 0,354913 0,98298 0,38127
yt=-1,415+0,653xt+0,349t
32. Автокорреляция в остатках Критерий Дарбина-Уотсона
• Коэффициент автокорреляции в остаткахn
et et 1 et et 1
rae
et et 1
rae
e e
t 2
n
t t 1
2
e
t
t 1
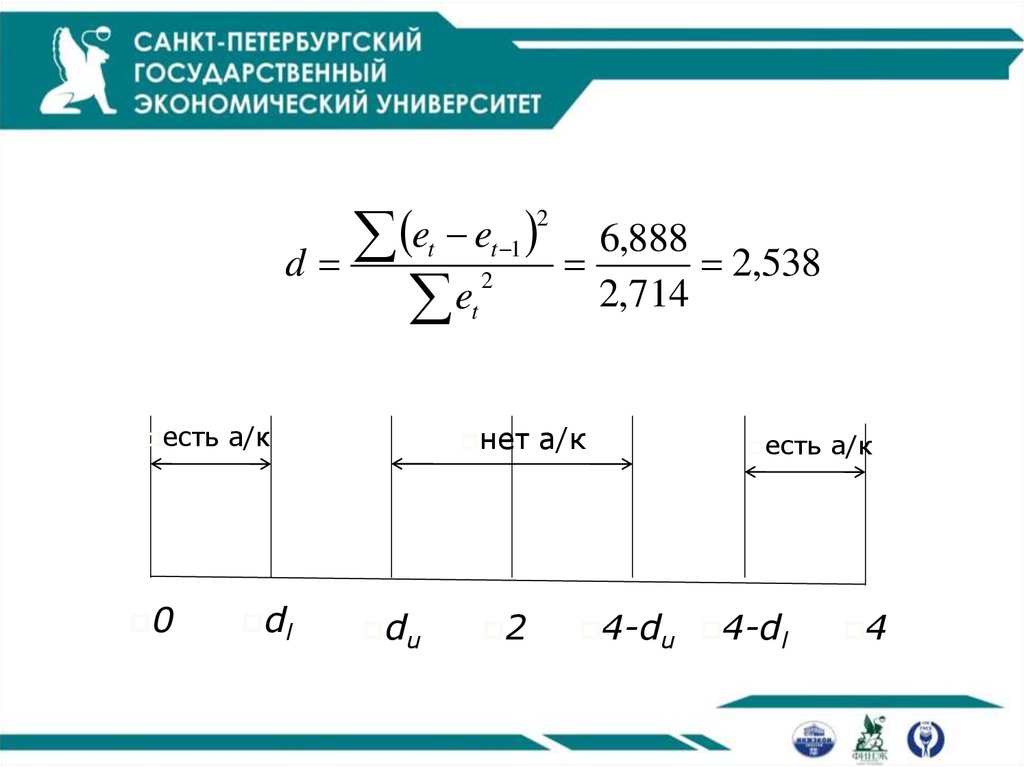
33. Критерий Дарбина-Уотсона
nd
2
(
e
e
)
t t 1
t 2
n
2
e
t
t 1
d 2(1 rae )
0 d 4
34. Пример
yˆt 5,857 1,07tt
yt
yˆ t
et
et 1
et et 1
et et 1 2
1
7
6,928571
0,071429
-
-
-
0,005102
2
8
8
0
0,071429
-0,07143
0,005102
0
3
10
9,071429
0,928571
0
0,928571
0,862245
0,862245
4
9
10,14286
-1,14286
0,928571
-2,07143
4,290816
1,306122
5
11
11,21429
-0,21429
-1,14286
0,928571
0,862245
0,045918
6
12
12,28571
-0,28571
-0,21429
-0,07143
0,005102
0,081633
7
14
13,35714
0,642857
-0,28571
0,928571
0,862245
0,413265
X
X
X
X
X
6,887755
2,714286
Итого
e e
d
e
2
t 1
2
t
t
6,888
2,538
2,714
et
2
35.
e ed
e
2
t 1
2
t
t
есть
0
нет
а/к
dl
du
2
6,888
2,538
2,714
а/к
есть
4-du 4-dl
а/к
4
36. Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам (ОМНК )
Алгоритм ОМНК1. Преобразование исходных
*
*
переменных
xt xt re xt 1
y y r y
t
2.
Применение обычного МНК к
уравнению и определение a*
и b
3.
Расчет параметра a
4.
Переход к исходному
уравнению
yt* a* bxt* Vt
a*
a
1 re
yt a bxt et
t
e t 1
37. Поправка Прайса-Винстена
1x x1 1 r
2
e
1
y y1 1 r
2
e
38.
dre 1
2
39. Пример По данным за 1995-2003 гг. по Тамбовской области рассматривается зависимость потребления растительного масла на душу населения (y, кг) от
потребленияовощей (x, кг)
Годы
yt
xt
et
et 1
y t*
x t*
1
1995
1996
1997
1998
1999
2000
2001
2002
2003
2
7,2
7,5
7,9
8,6
9,5
10,9
10,3
10,1
10,7
3
100
101
103
105
121
121
120
119
124
4
-0,272
-0,108
0,021
0,450
-0,818
0,582
0,117
0,053
-0,025
5
-0,272
0,108
0,021
0,450
-0,818
0,582
0,117
0,053
6
5,97
11,525
12,093
13,016
14,307
16,210
16,393
15,858
16,346
7
82,916
156,9
159,46
162,578
179,696
188,64
187,64
186,081
190,522
yˆt 6,0791 0,1355x
t
3,5
8,9
R 2 0,9188
re
F 79,2
et et 1 0,734
0,55901
2
1,314
et
40. Расчет преобразованных значений
y 7,2 1 ( 0,559) 5,97*
1
2
x1* 100 1 ( 0,559) 2 82,916
y 7,5 ( 0,559)7,2 11,525
*
2
x 101 ( 0,559)100 156,9
*
2
• и т.д.
41.
y 2,8156 0,0984 x*
R 2 0,961
*
F 172,3
a a* /(1 re ) 1,806
yˆ 1,806 0,0984 x
R2 0,845
re 0,239
42. Моделирование периодических колебаний
• Ряды могут содержать только периодические колебания• Ряды могут содержать и периодические колебания и
тенденцию
43.
• Для выявления измерения периодическихколебаний во временных рядах можно
использовать метод гармонического
анализа ряда
• Сущность метода состоит в представлении
функций в виде суммы гармонических
колебаний
44. Ряд Фурье
• Ряд Фурье -один из методов моделирования временногоряда с периодическими колебаниями
• Его построение зависит от наличия или отсутствия
тенденции в ряду динамики. При отсутствии тенденции
методика построения ряда Фурье применяется
непосредственно к уровням динамического ряда
Если же в ряду динамики наблюдается тенденция, то ряд
Фурье применяется к отклонениям от тенденции
45. Моделирование периодических колебаний
• Ряд Фурье можно описать в виде функции:yˆ t a0 a1 cos t b1 sin t a2 cos 2t b2 sin 2t
• Это ряд с двумя гармониками. Могут быть и 3 и 4 гармоники. Чаще
всего используется ряд Фурье не более чем с 4 гармониками.
0 - среднее значение ряда
a
• Параметры определяются с помощью МНК
46. Учет сезонности при построении модели регрессии
yt a bxt c1z1 c2 z2 c3 z3z1 = 1 – для первого квартала,
0 – для остальных;
z2 = 1 – для второго квартала,
0 – для остальных;
z3 = 1 – для третьего квартала,
0 – для остальных.
47. Переход от общего уравнения к уравнениям за каждый квартал
• для I квартала• для II квартала
• для III квартала
• для IV квартала
yt (a c1 ) bxt
yt (a c2 ) bxt
yt (a c3 ) bxt
yt a bxt
48. Пример. Объем продаж товара фирмой (у – тыс. ед.) исследуется в зависимости от объема продаж его дочерним предприятием (х – тыс. ед.) по данны
Пример. Объем продаж товара фирмой (у – тыс. ед.) исследуется взависимости от объема продаж его дочерним предприятием (х –
тыс. ед.) по данным за 5 лет
Кварталы
Годы
2006
2007
2008
2009
2010
Итого
В
среднем
I
у
11
11
10
10
11
53
10,6
II
х
9
10
7
12
8
46
9,2
у
15
16
14
16
18
79
15,8
Итого
III
х
10
9
10
9
16
54
10,8
у
6
4
7
8
7
32
6,4
IV
х
8
3
8
11
6
36
7,2
у
12
13
12
13
12
62
12,4
х
9
11
11
12
12
55
11
у
44
44
43
47
48
226
45,2
х
36
33
36
44
42
191
38,2
49.
годквартал
2006
2007
2008
2009
2010
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
1
2
3
4
yt
t
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
xt
11
15
6
12
11
16
4
13
10
14
7
12
10
16
8
13
11
18
7
12
z1
9
10
8
9
10
9
3
11
7
10
8
11
12
9
11
12
8
16
6
12
z2
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
z3
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
0
0
1
0
50.
ВЫВОД ИТОГОВyˆt 8,896 0,319 xt 1,227 z1 3,464 z2 4,789 z3
Регрессионная статистика
Множественный
0,977311
R
R-квадрат 0,955137
Нормированный
0,943173
R-квадрат
Стандартная0,865054
ошибка
Наблюдения
20
Дисперсионный анализ
df
SS
MS
F Значимость F
Регрессия
4 238,9752 59,74381 79,83739 6,32E-10
Остаток
15 11,22478 0,748319
Итого
19
250,2
Коэффициенты
Стандартная t-статистика
ошибка
P-Значение
Нижние 95%
Верхние 95%
Y-пересечение
8,895575 1,072979 8,290537 5,53E-07 6,608574 11,18258
xt
0,318584 0,090983 3,501588 0,003213 0,124659 0,512509
z1
-1,22655 0,571093 -2,14772 0,048484 -2,44381 -0,00929
z2
3,463717 0,547411 6,327455 1,36E-05 2,296938 4,630495
z3
-4,78938 0,647194 -7,40023 2,22E-06 -6,16884 -3,40992
51. Моделирование сезонных колебаний
yi T S E• Аддитивная модель
• Мультипликативная модель
yi T S E
• Приблизительно равная сезонная вариация указывает на
существование аддитивной модели.
• Усиление сезонной вариации с возрастанием тренда
указывает на существование мультипликативной модели.
52. Построение аддитивной модели
1. Нахождение сглаженных уровней динамического ряда методомскользящих средних;
2. Оценка сезонной компоненты и ее корректировка;
3. Элиминирование сезонной компоненты из исходных данных временного ряда;
4. Построение уравнения линейного тренда по уровням ряда с элиминированием сезонности;
5. Расчет выровненных значений трендовой составляющей;
6. Расчет теоретических уровней ряда с учетом сезонности;
7. Расчет случайной компоненты, позволяющий оценить качество построенной модели.
53. Пример
Количество проданной продукции в течение последних 13 кварталовТаблица 1
Год
I
II
III
IV
Квартал
1
2
3
4
1
2
3
4
1
2
3
4
1
Объем продаж,
тыс. шт
239
201
182
297
324
278
257
384
401
360
335
462
481
54.
Объем продаж, тыс. шт.Объем продаж
600
500
400
300
Объем продаж
200
100
0
1
2
3
4 5
6
7
8
Квартал
9 10 11 12 13
55. Расчет сезонной компоненты в аддитивной модели
ГодКвартал
1
2
1
2
I
3
4
1
II
2
3
4
1
III
2
3
IV
4
1
Объем
Скользящая
Центрированная
продаж
средняя за 4 скользящая
тыс.
шт
квартала
средняя
Yt
3
4
5
239
201
229,75
182
240,4
251
297
260,6
270,25
324
279,6
289
278
299,9
310,75
257
320,4
330
384
340,3
350,5
401
360,3
370
360
379,8
389,5
335
399,5
409,5
462
481
-
Оценка
сезонной
компоненты
6=3-5
-58,4
36,4
44,4
-21,9
-63,4
43,8
40,8
-19,8
-64,5
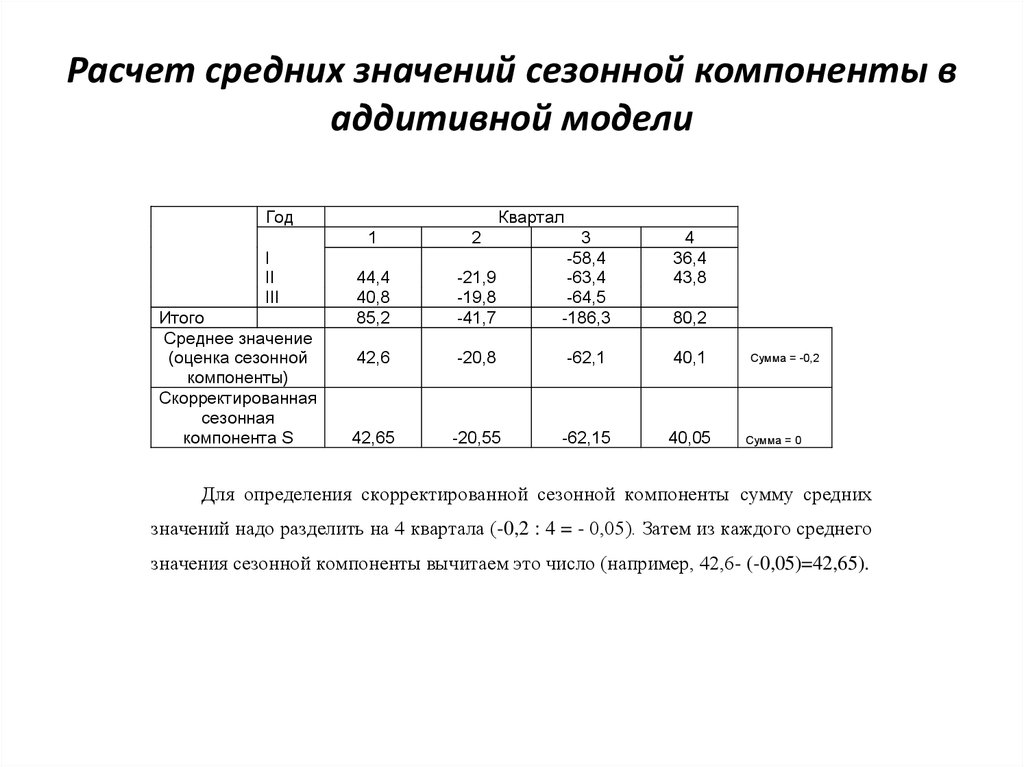
56. Расчет средних значений сезонной компоненты в аддитивной модели
КварталГод
I
II
III
Итого
Среднее значение
(оценка сезонной
компоненты)
Скорректированная
сезонная
компонента S
-21,9
-19,8
-41,7
3
-58,4
-63,4
-64,5
-186,3
4
36,4
43,8
42,6
-20,8
-62,1
40,1
42,65
-20,55
-62,15
40,05
1
2
44,4
40,8
85,2
80,2
Сумма = -0,2
Сумма = 0
Для определения скорректированной сезонной компоненты сумму средних
значений надо разделить на 4 квартала (-0,2 : 4 = - 0,05). Затем из каждого среднего
значения сезонной компоненты вычитаем это число (например, 42,6- (-0,05)=42,65).
57.
Год1
I
II
III
IV
Десезона
лизирова
Скоррект нный
ированна объем
продаж,
Объем
я
продаж сезонная тыс.шт.
тыс. шт компонен Yt - S=T+
Квартал
та S
E
Yt
2
3
4
5=3-4
1
239
42,65
196,35
2
201
-20,55
221,55
3
182
-62,15
244,15
4
297
40,05
256,95
1
324
42,65
281,35
2
278
-20,55
298,55
3
257
-62,15
319,15
4
384
40,05
343,95
1
401
42,65
358,35
2
360
-20,55
380,55
3
335
-62,15
397,15
4
462
40,05
421,95
1
481
42,65
438,35
r2 1
T
T+S
E=yt-(T+S)
6
7=6+4
8=3-7
199,998 242,648
219,977 199,427
239,957 177,807
259,936 299,986
279,915 322,565
299,894 279,344
319,873 257,723
339,852 379,902
359,831 402,481
379,810 359,260
399,790 337,640
419,769 459,819
439,748 482,398
79,884
0,9992
104481,692
-3,648
1,573
4,193
-2,986
1,435
-1,344
-0,723
4,098
-1,481
0,740
-2,640
2,181
-1,398
E2
y t y n 2
9
13,310
2,473
17,585
8,914
2,060
1,806
0,523
16,792
2,194
0,547
6,967
4,758
1,954
10
7081,896
14921,600
19924,452
684,032
0,716
2038,884
4376,352
3702,236
6060,000
1357,628
140,328
19278,212
24915,360
79,884
104481,692
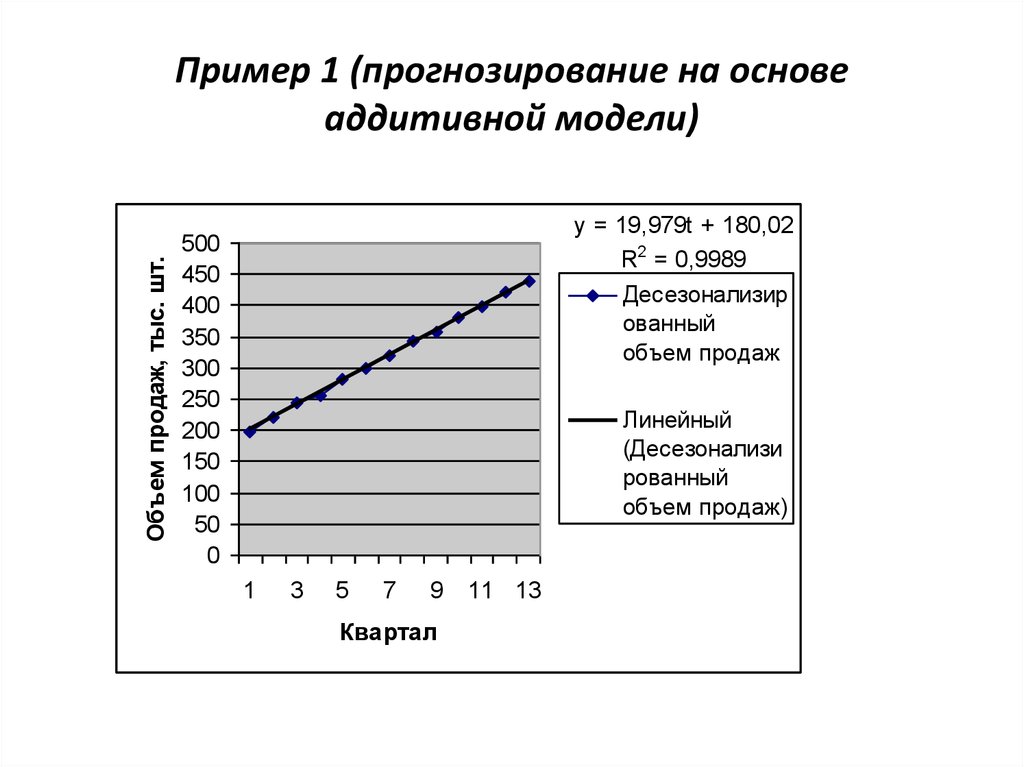
58. Пример 1 (прогнозирование на основе аддитивной модели)
Объем продаж, тыс. шт.Пример 1 (прогнозирование на основе
аддитивной модели)
y = 19,979t + 180,02
R2 = 0,9989
Десезонализир
ованный
объем продаж
500
450
400
350
300
250
200
150
100
50
0
Линейный
(Десезонализи
рованный
объем продаж)
1
3
5
7
9
Квартал
11 13
59.
Прогнозирование по тренду с учетом сезонной компонентыГод
1
IV
Трендовый
Квартал
прогноз
2
1
2
3
4
3
438,35
460,20
480,20
500,20
Скорректированная
сезонная
компонента S
4
42,65
-20,55
-62,15
40,05
Прогноз с
учетом
сезонной
компоненты
5=3+4
481,00
439,65
418,05
540,25
60. Пример 2 Построение мультипликативной модели
Количество проданной продукции в течение последних 13 кварталовГод
Квартал
Объем продажт тыс.
Yt
шт
1
2
1
2
3
4
1
2
3
4
1
2
3
4
1
3
70
66
65
71
79
66
67
82
84
69
72
87
94
I
II
III
IV
61.
Объем продаж, тыс. шт.Объем продаж тыс. шт
100
80
60
Объем продаж
тыс. шт
40
20
0
1
3
5
7
9
Квартал
11 13
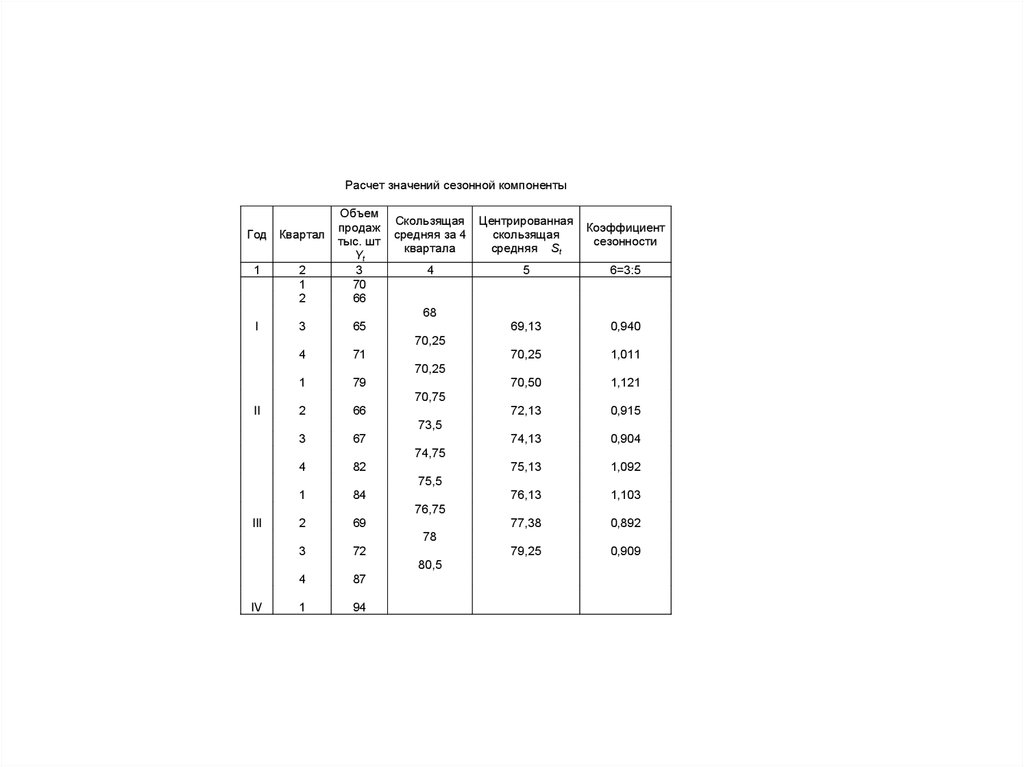
62.
Расчет значений сезонной компоненты1
2
1
2
Объем
продаж
тыс. шт
Yt
3
70
66
I
3
65
Год Квартал
Скользящая
средняя за 4
квартала
Центрированная
скользящая
средняя St
Коэффициент
сезонности
4
5
6=3:5
69,13
0,940
70,25
1,011
70,50
1,121
72,13
0,915
74,13
0,904
75,13
1,092
76,13
1,103
77,38
0,892
79,25
0,909
68
70,25
4
71
70,25
1
79
70,75
II
2
66
73,5
3
67
74,75
4
82
75,5
1
84
76,75
III
2
69
78
3
72
80,5
IV
4
87
1
94
63.
Расчет средних значений сезонной компонентыГод
I
II
III
Итого
Среднее значение
(оценка сезонной
компоненты)
Скорректированна
я сезонная
компонента S
Квартал
1
2
0,915
0,892
1,807
3
0,94
0,904
0,909
2,753
4
1,011
1,092
1,121
1,103
2,224
2,224:2=1,112
1,807:2=0,903
2,753:3=0,918
2,103:2=1,051
Сумма =
3,984
1,116
0,907
1,055
Сумма = 4
0,922
k 4 / 3,984 1,004
2,103
64.
Год1
I
II
III
IV
Скоррек
тирован Десезонали
ная
зированны
Объем
продажт сезонная й объем
тыс. шт компоне продаж,
Квартал
нта S
тыс.шт.
Yt
2
3
4
5=3:4
1
70
1,116
62,7
2
66
0,907
72,8
3
65
0,922
70,5
4
71
1,055
67,3
1
79
1,116
70,8
2
66
0,907
72,8
3
67
0,922
72,7
4
82
1,055
77,7
1
84
1,116
75,3
2
69
0,907
76,1
3
72
0,922
78,1
4
87
1,055
82,5
1
94
1,116
84,2
E=yt/(T*
S)
T*S
T
6
7=6*4
8=3/7
65,933
73,581
0,951
67,2967
61,038
1,081
68,6604
63,305
1,027
70,0242
73,876
0,961
71,3879
79,669
0,992
72,7516
65,986
1,000
74,1154
68,334
0,980
75,4791
79,630
1,030
76,8429
85,757
0,980
78,2066
70,933
0,973
79,5703
73,364
0,981
80,9341
85,385
1,019
82,2978
91,844
1,023
65.
y = 1,3634t + 64,562R2 = 0,8209
90,00
80,00
70,00
60,00
50,00
Ряд1
40,00
Линейный (Ряд1)
30,00
20,00
10,00
0,00
1
2
3
4
5
6
7
8
9 10 11 12 13
66.
Объем продаж, тыс. шт.Квартальные объемы продаж компании
100
80
Объем продажт
60
Десезонализирован
ный объем продаж,
40
20
0
1 2 3 4 5 6 7 8 9 10 11 12 13
Квартал
67. Пример 2 (прогнозирование на основе мультипликативной модели)
Прогнозирование по тренду с учетом сезонной компонентыГод
Квартал
1
2
1
2
3
4
IV
Скорректированная
Трендовый
сезонная
прогноз
компонента S
3
84,23
83,64
85
86,36
4
1,116
0,907
0,922
1,055
Прогноз с
учетом
сезонной
компоненты
5=3*4
94,00
75,86
78,37
91,11
68. Модели с лаговыми переменными
• 1) модели с лаговыми объясняющими переменными или иначемодели с распределенными лагами
yt a b0 xt b1xt 1 ... bk xt k et
• 2) модели с лаговыми зависимыми переменными – модели
авторегрессии
yt a bxt c1 yt 1 ... ck yt k et
• 3) модели с лаговыми зависимыми и независимыми переменными, т.
е. авторегрессионные модели с распределенными лагами
yt a b1 yt 1 ... bk yt k c0 xt c1xt 1 ... ck xt k et
69. Модель с распределенными лагами
yˆt a b0 xt b1xt 1 b2 xt 2 b3 xt 3 b4 xt 4• Данная модель означает, что изменение во времени t
объясняющей переменный x будет влиять на значения
результативного признака y в течение 4-х следующих
моментов времени
70.
• Коэффициент b0- краткосрочный мультипликатор. Онхарактеризует среднее изменение результата y при
изменении на 1 единицу своего измерения в
фиксированный момент времени t.
• В момент времени t+1 воздействие объясняющей
переменной x на результат y составит ( b0 b1 ) единиц, а
в момент времени t+2 общее изменение y составит
( b0 b1 b2 ) единиц.
71. Промежуточные мультипликаторы
• при k=4:b0 b1
b0 b1 b2
b0 b1 b2 b3
- изменение y в момент времени t+1;
- изменение y в момент времени t+2;
- изменение y в момент времени t+3.
72.
• Долгосрочный мультипликаторk
b
j 0
j
• При k=4 долгосрочный мультипликатор составит
b0 b1 b2 b3 b4
• Он характеризует общее среднее изменение y через 4
временных интервала при увеличении x в момент
времени t на 1 единицу
73. Относительные коэффициенты модели
j• Характеризует долю общего изменения y в
момент времени t+j.
j
bj
b
j
0 j 1
j
1
74. Средняя величина лага
kj j j
j 0
• Показывает средний интервал времени, в течение которого будет
происходить изменение зависимой переменной y под воздействием
изменения объясняющей переменной x в момент времени t.
• Чем меньше величина среднего лага, тем быстрее реагирует результат
y на изменение x. И наоборот, высокое значение среднего лага
показывает, что воздействие объясняющей переменной на результат
будет сказываться с течением длительного промежутка времени.
75. Медианный лаг
• тот период времени, в течение которого смомента времени t будет реализована половина
общего эффекта воздействия объясняющей
переменной x на результат yt.
Me
j 0
j
0,5
76. Пример
yˆ t 0,8 0,7 xt 1,0 xt 1 1,5 xt 2 0,6 xt 3 0,2 xt 4• где t – время в годах, yt - основные
производственные фонды ( млн. руб.),
• xt - размер инвестиций (млн. руб.)
77.
• Рост инвестиций на 1 млн. руб. в текущем периоде приводит к ростуосновных производственных фондов:
• - в том же периоде на 0,7 млн. руб. (краткосрочный мультипликатор);
• - через 1 год на 0,7+1=1,7 млн. руб.;
• - через 2 года на 0,7+1+1,5=3,2 млн. руб.;
• - через 3 года на 3,8 млн. руб. (промежуточный, как и предыдущие
два, мультипликатор);
• - через 4 года на 4 млн. руб. (долгосрочный мультипликатор).
78.
• Относительные коэффициенты модели:0 = 0,7 / 4 = 0,175;
1 = 1 / 4 = 0,25;
2 = 1,5 / 4 = 0,375;
3 = 0,6 / 4 = 0,15;
4 = 0,2 / 4 = 0,05.
• В текущем году реализуется 17,5% воздействия увеличения
инвестиций на рост основных производственных фондов, а через год
еще 25%. Через 2 года – еще 37,5%, через 3 года – еще 15% и через 4
года – еще 5%.
79.
• j = 0 ∙ 0,175 + 1 ∙ 0,25 + 2 ∙ 0,375 + 3 ∙ 0,15 + 4 ∙ 0,05 = 1,65 года.• Основная часть эффекта увеличения инвестиций проявляется через
1,65 года.
• Медианный лаг составляет два года, т. е. увеличение инвестиций в
период времени t на 1 млн. руб. приводит к росту размера основных
производственных фондов через 2 года на величину, составляющую
половину долгосрочного мультипликатора, т. е. на 2 млн. руб.
80. Модели авторегрессии
yt a b0 xt с1 yt 1 et• параметр b0 характеризует краткосрочное изменение yt под
воздействием изменения xt на 1 единицу.
• долгосрочный мультипликатор изменения y:
b0
b
1 c1











































































 mathematics
mathematics








