Анализ временных рядов

1. Data Science

Анализ временных рядов
MVP
DEDICATED
TEAM
SUPPORT

2. Лекция

11.11.2002
04.11.2002
28.10.2002
21.10.2002
14.10.2002
07.10.2002
30.09.2002
23.09.2002
16.09.2002
09.09.2002
02.09.2002
26.08.2002
19.08.2002
12.08.2002
05.08.2002
29.07.2002
22.07.2002
15.07.2002
08.07.2002
01.07.2002
24.06.2002
17.06.2002
10.06.2002
03.06.2002
27.05.2002
20.05.2002
13.05.2002
06.05.2002
29.04.2002
22.04.2002
15.04.2002
08.04.2002
01.04.2002
Лекция
Анализ временных рядов
3,50E+09
3,00E+09
2,50E+09
2,00E+09
1,50E+09
1,00E+09
5,00E+08
0,00E+00

3. Анализ временных рядов

временным рядом называют
последовательность наблюдений,
упорядоченных по времени
Аргумент (t) дискретно меняется через равные
промежутки.

4. Визуализация временного ряда

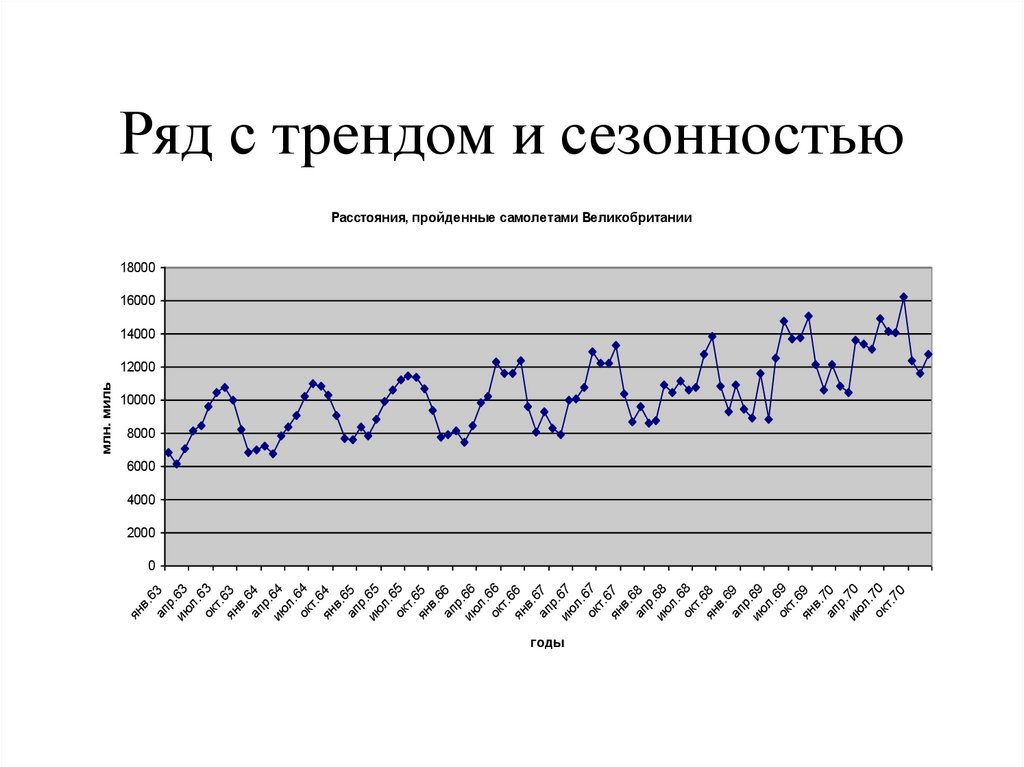
месячные международные авиаперевозки
в течение 12 лет.
(Бокс и Дженкинс, 1976, стр. 531)

5. Модели временных рядов.

Такие модели объясняют поведение
переменной, меняющейся с течением
времени, исходя только из ее
предыдущих значений. К этому классу
относятся модели тренда, сезонности,
тренда и сезонности (аддитивная и
мультипликативная формы) и др.

6. Модель временного ряда

случайная
составляющая
тренд
Y(t) = f(t)+g(t)+ (t)
периодическая
(сезонная)
составляющая

7. Ряд с трендом и сезонностью

ян
в.
6
ап 3
р.
ию 63
л.
6
ок 3
т.6
ян 3
в.
6
ап 4
р.
ию 64
л.
ок 64
т.6
ян 4
в.
6
ап 5
р.
ию 65
л.
6
ок 5
т.6
ян 5
в.
6
ап 6
р.
ию 66
л.
ок 66
т.6
ян 6
в.
6
ап 7
р.
ию 67
л.
ок 67
т.6
ян 7
в.
6
ап 8
р.
ию 68
л.
6
ок 8
т.6
ян 8
в.
6
ап 9
р
ию .69
л.
ок 69
т.6
ян 9
в.
7
ап 0
р.
ию 70
л.
ок 70
т.7
0
млн. миль
Ряд с трендом и сезонностью
Расстояния, пройденные самолетами Великобритании
18000
16000
14000
12000
10000
8000
6000
4000
2000
0
годы

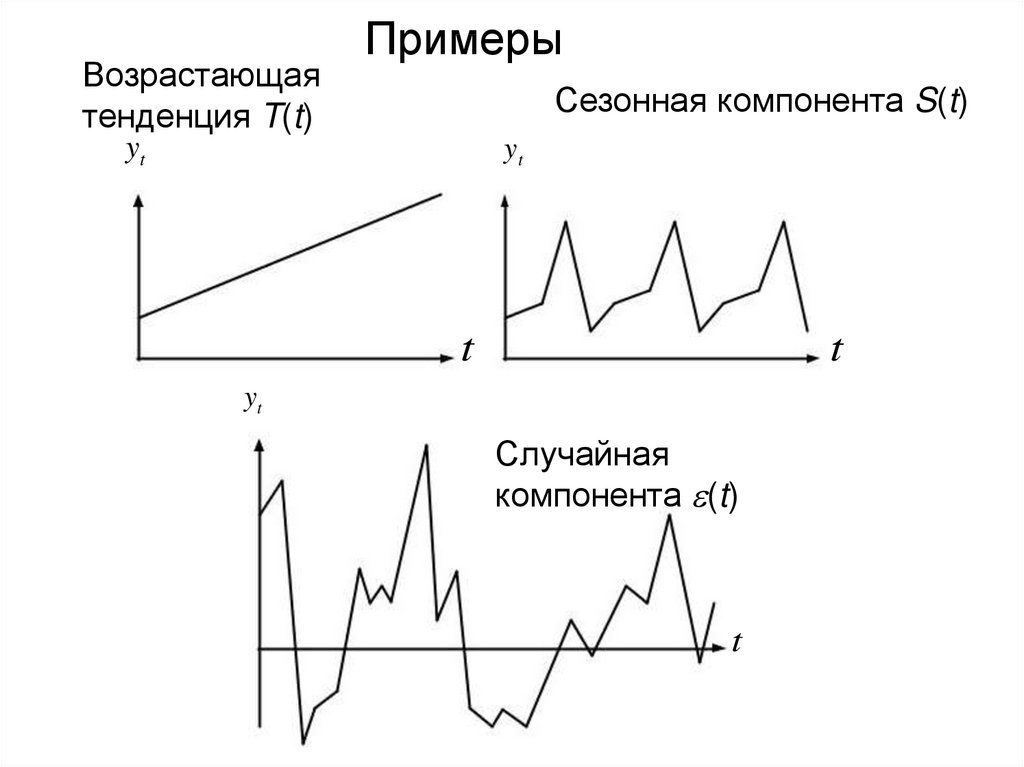
8.

Возрастающая
тенденция T(t)
Примеры
Сезонная компонента S(t)
yt
yt
t
t
yt
Случайная
компонента (t)
t

9.

Модель, в которой временной ряд представлен
как сумма перечисленных компонент, называется
аддитивной моделью временного ряда.
Модель, в которой временной ряд представлен
как произведение перечисленных компонент,
называется мультипликативной моделью
временного ряда.

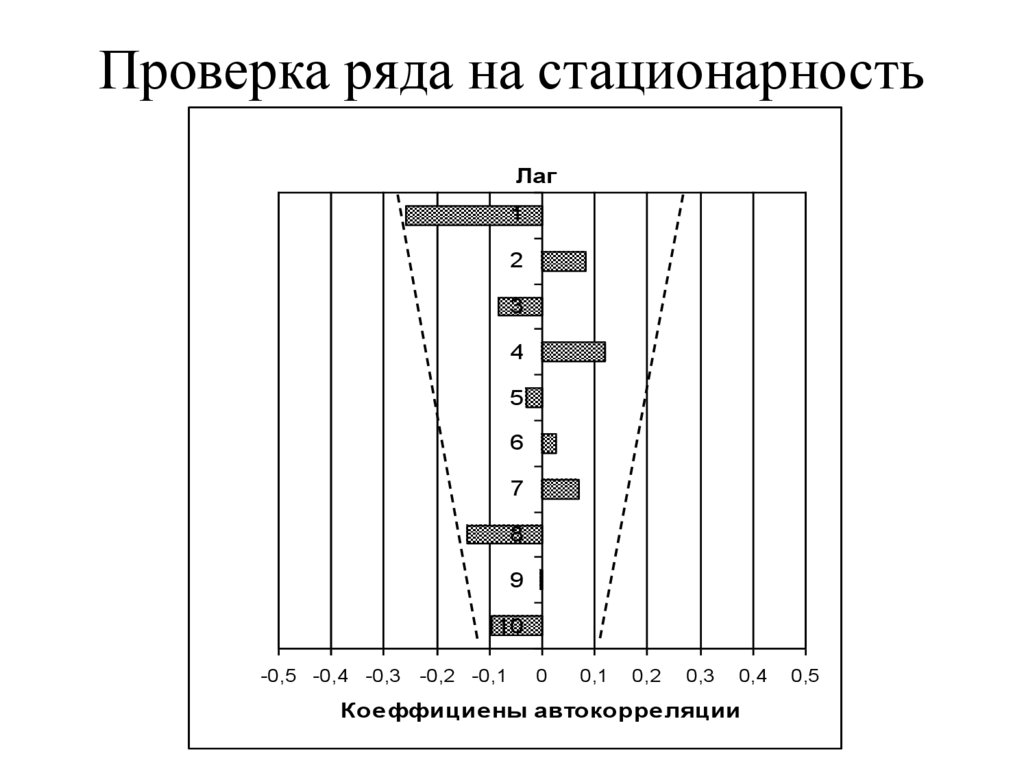
10. Стационарность ряда

Ряд называется слабо стационарным или
просто стационарным, если средние,
дисперсии и ковариации не зависят от
времени t.

11. Стационарный случайный процесс

1.Математическое ожидание постоянно
(стационарность в широком смысле).
2. Автокорреляционная функция зависит
только от разности аргумента.
В.Е. Гмурман. Теория вер. и мат. статистика. Стр. 386-449

12.

Автокорреляция уровней
временного ряда
Автокорреляция элементов временного ряда –
корреляционная зависимость между последовательными
элементами временного ряда.
Лаг – число периодов, по которым рассчитывается
коэффициент автокорреляции между парами элементов ряда.
Автокорреляционная функция временного ряда –
последовательность коэффициентов автокорреляции с лагами,
равными 1, 2, 3 ….
Замечание. С увеличением лага число пар значений, по
которым рассчитывается коэффициент автокорреляции
уменьшается. Для статистической достоверности используется
правило: максимальный лаг не больше n/4.

13. Проверка ряда на стационарность

Лаг
1
2
3
4
5
6
7
8
9
10
-0,5 -0,4 -0,3
-0,2 -0,1
0
0,1
0,2
0,3
0,4
Кое ффицие ны автокорре ляции
0,5

14.

• Коэффициент автокорреляции остатков
первого порядка определяется по формуле:
n
r1
t 2
t
t 1
n
2
t
t 2
• Критерий Дарбина-Уотсона и коэффициент
автокорреляции остатков первого порядка
связаны соотношением
d 2(1 r1 )

15. Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона:

1. Выдвигаются гипотезы:
• Гипотеза H0 об отсутствии автокорреляции
остатков.
• Гипотеза H1 о наличии положительной
автокорреляции в остатках.
• Гипотеза H1* о наличии отрицательной
автокорреляции в остатках.

16.

2. По специальным таблицам определяются
критические значения критерия ДарбинаУотсона dL и dU для заданного числа
наблюдений n (начиная со второго значения),
числа независимых переменных k и уровня
значимости . По этим значениям числовой
промежуток 0;4 разбивают на 5 отрезков.

17. Алгоритм проверки гипотезы о наличии автокорреляции остатков

Есть
Зона
положительная
неопре
автокорреляция деленостатков. Н0
ности
отклоняется. С
вероятностью
P=(1- )
принимается Н1
0
dL
Зона
Нет
оснований неопреде
ленотклонять
Hо.
ности
Автокорре
-ляция
отсутствуе
т
dU
2 4 d
U
Есть
отрицательная
автокорреляция
остатков. Н0
отклоняется. С
вероятностью
P =(1- )
принимается Н1*
4 dL
4

18.

Следующие тесты проверяют стационарность
ряда. Это расширенный тест Дики–Фуллера
(ADF). Еще один очень часто используемый тест,
тест Филлипса–Перрона (PP). Оба теста
проверяют нулевую гипотезу о
нестационарности процесса при альтернативной
гипотезе о том, что процесс стационарен. Тест
Филлипса–Перрона учитывает возможность
гетероскедастичности ошибок
Рассчитанная ADF-статистика сравнивается с N процентным (N=5%, 1%)
уровнем значимости и на основе данного сравнения делается вывод о
стационарности/нестационарности ряда.

19.

ВЫЯВЛЕНИЕ СТРУКТУРЫ РЯДА:
•Если наиболее высоким оказался коэффициент
автокорреляции первого и/или второго порядка,
исследуемый ряд содержит только тенденцию.
•Если все коэффициенты автокорреляции оказались
значимыми (высокими), то исследуемый ряд содержит
только тенденцию.
•Если наиболее высоким оказался коэффициент
автокорреляции порядка t , ряд содержит циклические
колебания с периодичностью в t моментов времени.

20. Обнаружение нестационарности

ОБНАРУЖЕНИЕ
НЕСТАЦИОНАРНОСТИ
Визуальный анализ временного ряда.
Возможно, временной ряд содержит видный
на глаз временной тренд и сезонность
(периодичную компоненту). Возможно, что
разброс значений возрастает или убывает со
временем (признак «случайного блуждания»).
Это может служить указанием на зависимость
среднего и, соответственно, дисперсии от
времени. Во всех трех случаях ряд, скорее
всего, не будет стационарным.

21. Избавление от нестационарности

ИЗБАВЛЕНИЕ ОТ
НЕСТАЦИОНАРНОСТИ
• Выделить тренд и сезонность, т. е.
неслучайную составляющую временного
ряда.
• Если ряд представляет «случайное
блуждание», то взятие последовательных
разностей делает ряд стационарным. На
практике порядок разностей, как
правило, не больше двух.

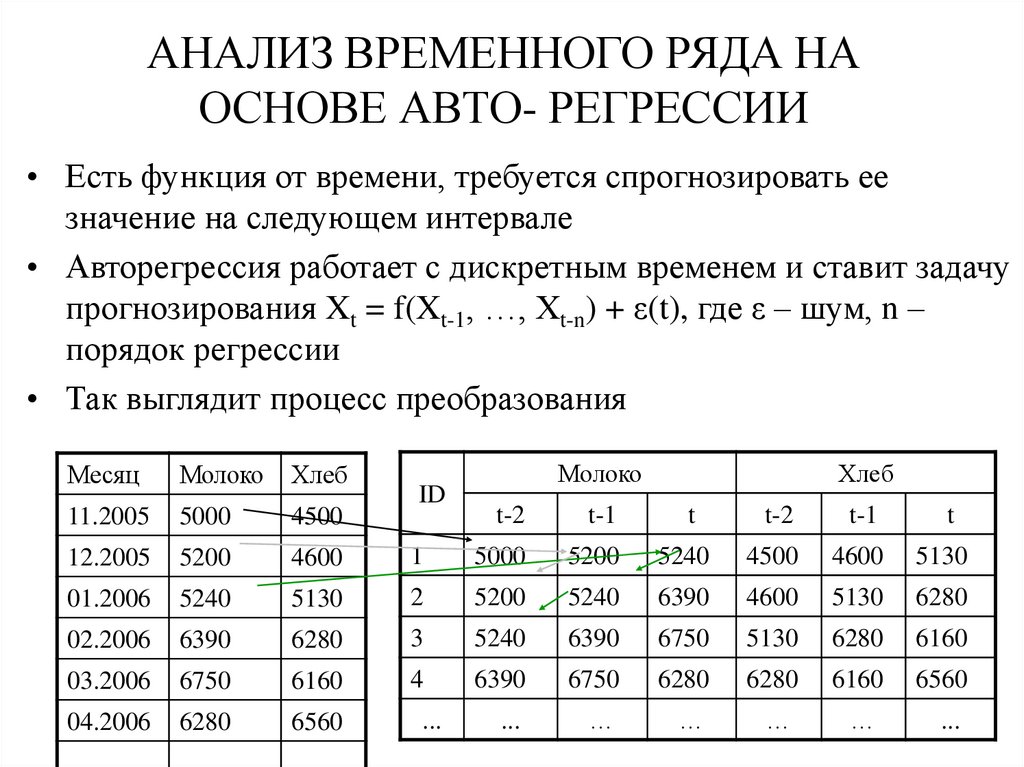
22. Анализ временного ряда на основе авто- регрессии

АНАЛИЗ ВРЕМЕННОГО РЯДА НА
ОСНОВЕ АВТО- РЕГРЕССИИ
• Есть функция от времени, требуется спрогнозировать ее
значение на следующем интервале
• Авторегрессия работает с дискретным временем и ставит задачу
прогнозирования Xt = f(Xt-1, …, Xt-n) + ε(t), где ε – шум, n –
порядок регрессии
• Так выглядит процесс преобразования
Месяц
Молоко
Хлеб
11.2005
5000
4500
12.2005
5200
4600
01.2006
5240
02.2006
ID
Молоко
t-2
t-1
1
5000
5200
5130
2
5200
6390
6280
3
03.2006
6750
6160
4
04.2006
6280
6560
...
Хлеб
t
t-2
t-1
t
5240
4500
4600
5130
5240
6390
4600
5130
6280
5240
6390
6750
5130
6280
6160
6390
6750
6280
6280
6160
6560
...
…
…
…
…
...

23. Анализ временного ряда

АНАЛИЗ ВРЕМЕННОГО РЯДА
• В случае линейной авторегрессии уравнение приобретает
вид X(t) = a1X(t-1) + a2X(t-2) + ... + anX(t-n) + ε(t)
• Для нахождения коэффициентов авторегрессии используется
метод Юля – Уолкера (Yule – Walker, 1927 г.) минимизации
среднеквадратичного отклонения между модельным и
наблюдаемым временным рядом

24.

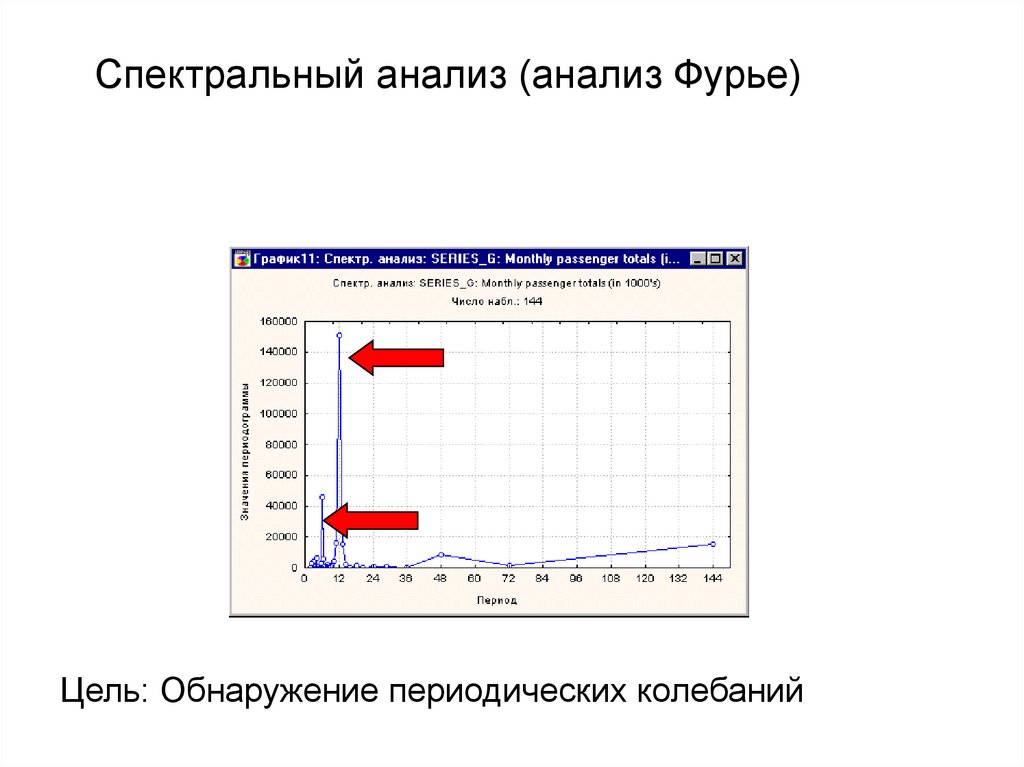
Спектральный анализ (анализ Фурье)
Цель: Обнаружение периодических колебаний

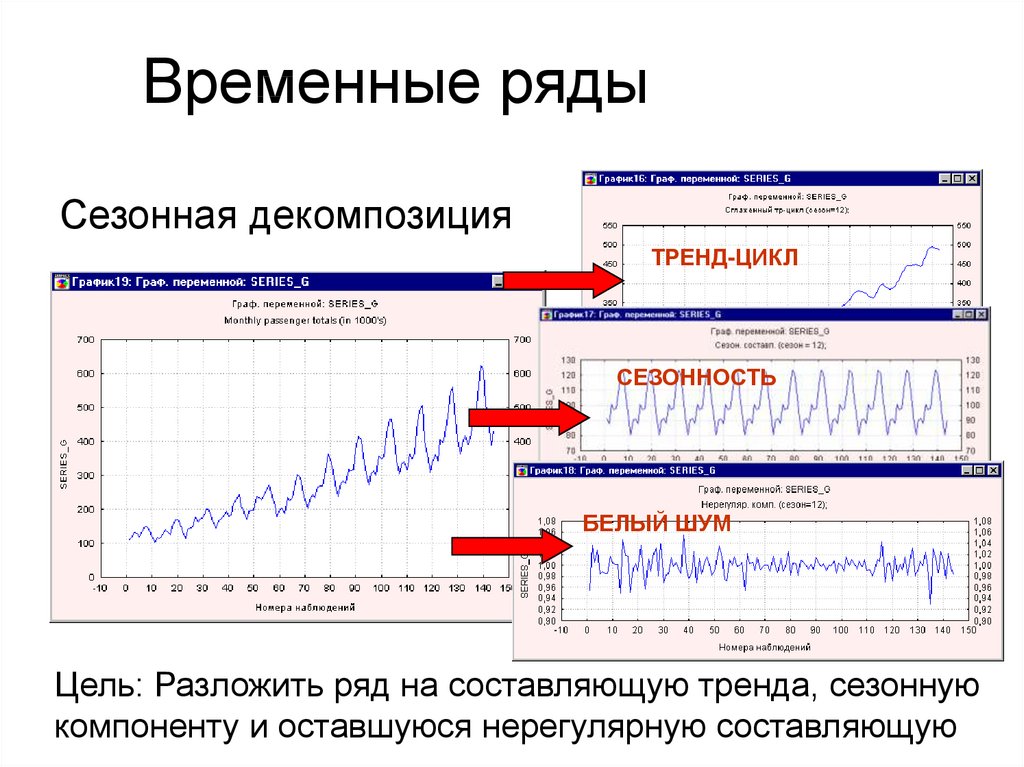
25. Временные ряды

Сезонная декомпозиция
ТРЕНД-ЦИКЛ
СЕЗОННОСТЬ
БЕЛЫЙ ШУМ
Цель: Разложить ряд на составляющую тренда, сезонную
компоненту и оставшуюся нерегулярную составляющую

26. Модели стационарных временных рядов

Модели Бокса-Дженкинса.
Модели авторегрессии и скользящего
среднего ARMA(p,q)

27. ARMA(p,q)

Yt 1Yt 1 ... pYt p t 1 1 ... q t q
t ~ iid(0, 2 )
процесс авторегрессии порядка p и скользящего
среднего порядка q –ARMA(p,q)
p
Yt
1
q
t
1
-авторегрессионный член порядка p
-член скользящего среднего порядка q

28. Анализ стационарных временных рядов

Спецификация ARMA-моделей.
Оценивание модели.
Проверка адекватности модели.
Прогнозирование на основе
построенной модели.

29. Спецификация ARMA-моделей.

• Определение p и q.
Для этого можно построить графики
автокорреляционной функции и частной
автокорреляционной функции ряда для того,
чтобы определить подходящие значения p и q.
Автокорерляционные функции и частные
автокорреляционные функции процессов AR(1),
AR(2), MA(1), MA(2) и ARMA(1,1) легко опознать.

30. Спецификация ARMA-моделей (продолжение)

На этом этапе мы можем сформулировать
несколько гипотез относительно
возможных значениях порядков p и q. Для
подходящих значений автокорреляционная
функция остатков ARMA(p,q) – модели
похожа на «белый шум».

31. Оценивание модели

В современные пакеты встроены
различные методы оценивания ARIMA –
моделей, такие как линейный или
нелинейный МНК. полный или условный
метод максимального правдоподобия.

32. Проверка адекватности модели

Необходимо проверить правильность
предположений относительно параметров
модели. Для этого
• проверяем статистическую значимость
коэффициентов модели должны
достоверно отличатся от нуля
• проверяем отсутствие автокорреляции в
остатках ARMA(p,q) – модели

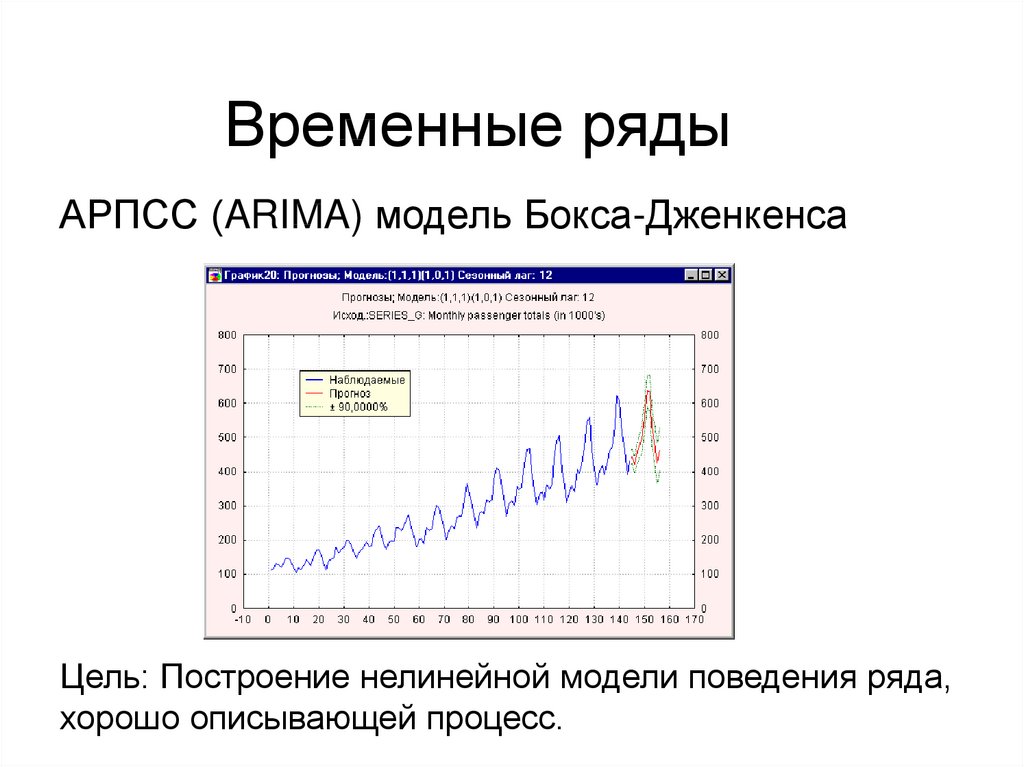
33. Временные ряды

АРПСС (ARIMA) модель Бокса-Дженкенса
Цель: Построение нелинейной модели поведения ряда,
хорошо описывающей процесс.

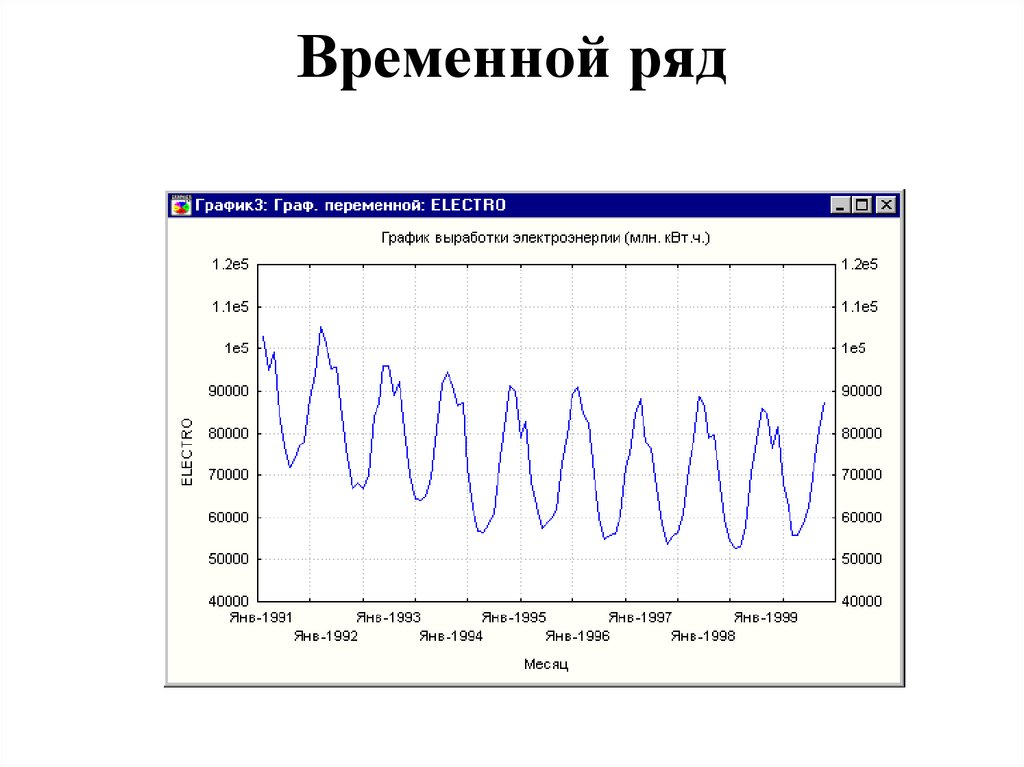
34. Временной ряд

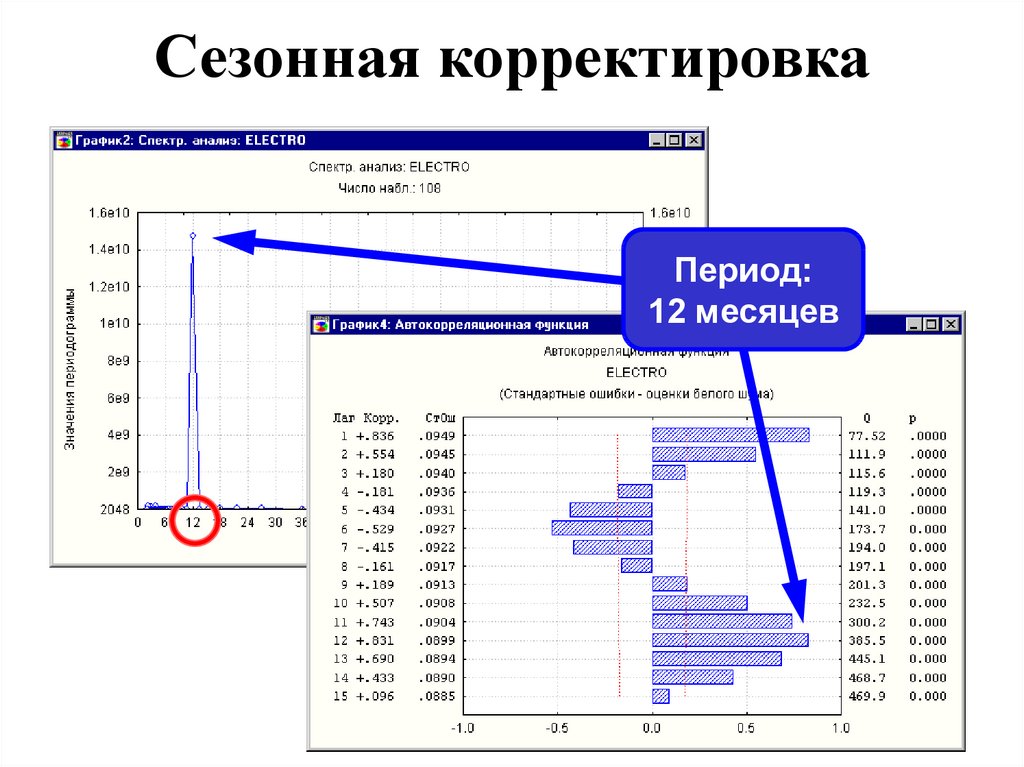
35. Сезонная корректировка

Период:
12 месяцев

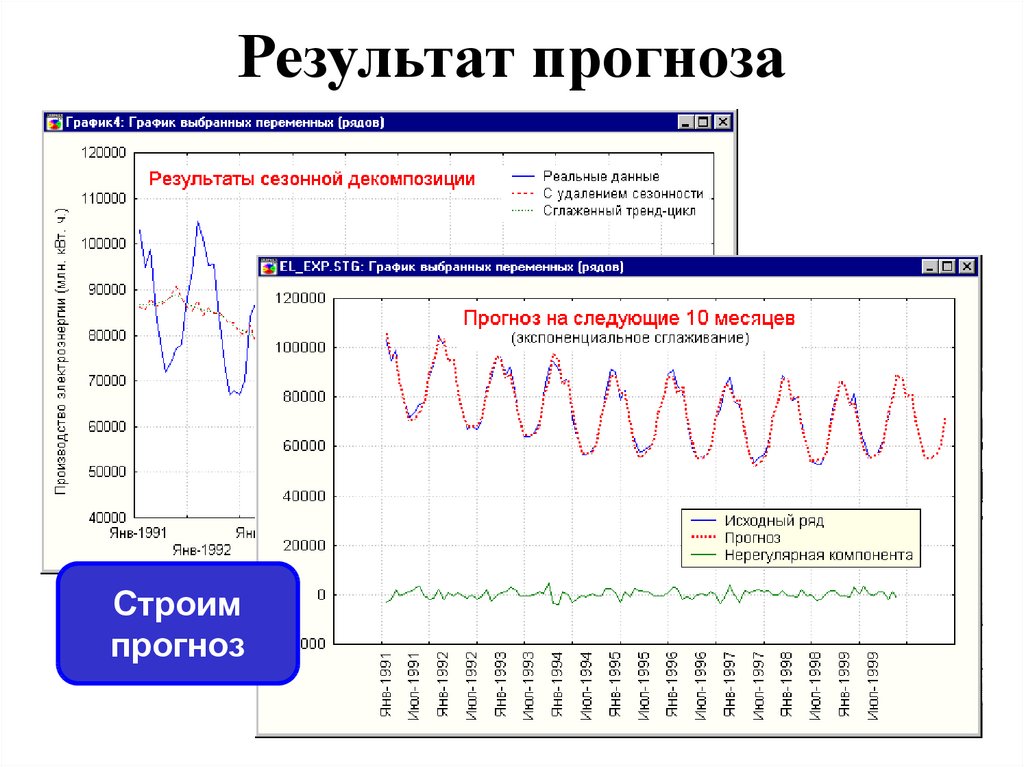
36. Результат прогноза

Строим
прогноз

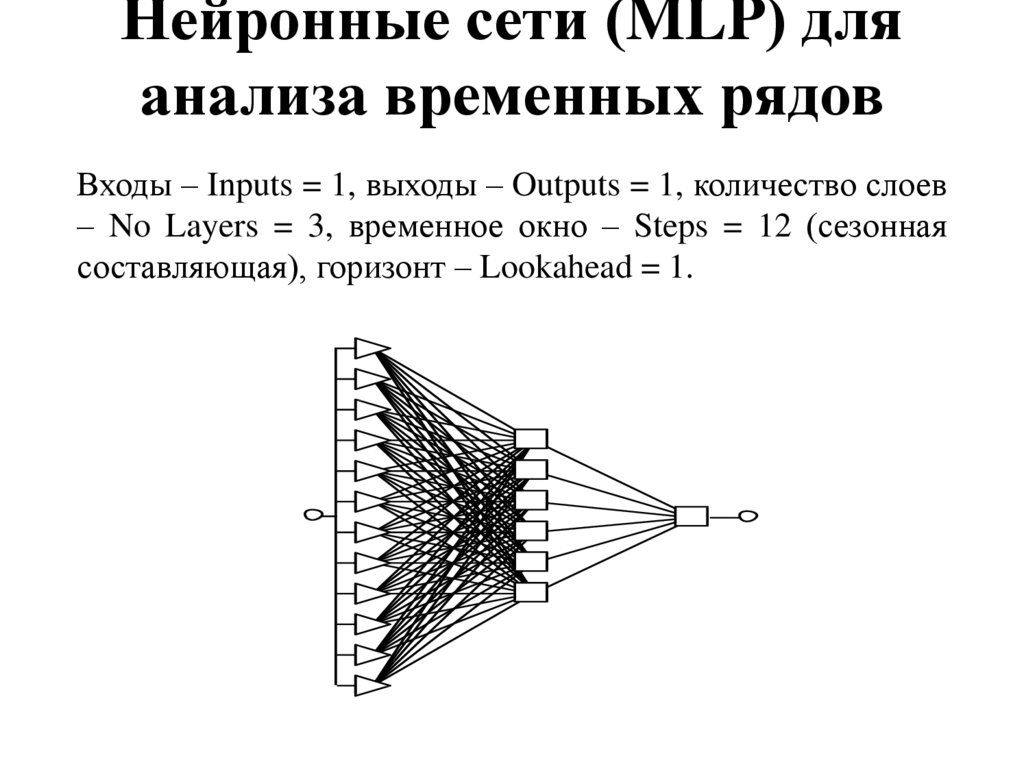
37. Нейронные сети (MLP) для анализа временных рядов

Входы – Inputs = 1, выходы – Outputs = 1, количество слоев
– No Layers = 3, временное окно – Steps = 12 (сезонная
составляющая), горизонт – Lookahead = 1.

38. ВОПРОСЫ?