Представление чисел в компьютере

1.

ПД.03 ИНФОРМАТИКА
И ИКТ

2.

12. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В
КОМПЬЮТЕРЕ

3.

Содержание
1.Понятие систем счисления?
2.Представление чисел в компьютере.
• Вещественные числа
• Три формы записи (кодирования) целых чисел со знаком
• Дополнительный код
• Арифметические операции над числами с плавающей
запятой

4.

Система счисления
– называется совокупность символов (цифр) и правил их
использования для представления чисел
Используются два типа систем счисления:
• позиционная – представление числа зависит от порядка записи
цифр.
• непозиционная – представление числа не зависит от порядка
записи цифр

5.

Представление чисел в компьютере
• Для представления чисел в памяти компьютера используются два
формата: формат с фиксированной точкой и формат с плавающей
точкой. В формате с фиксированной точкой представляются только
целые числа, в формате с плавающей точкой – вещественные числа
(целые и дробные).
• Целые числа могут представляться в компьютере со знаком или без
знака.
• Целые числа без знака обычно занимают в памяти один или два байта.
• Целые числа со знаком обычно занимают в памяти компьютера один,
два или четыре байта, при этом самый левый (старший) разряд
содержит информацию о знаке числа. Знак "плюс" кодируется нулем, а
"минус" - единицей.

6.

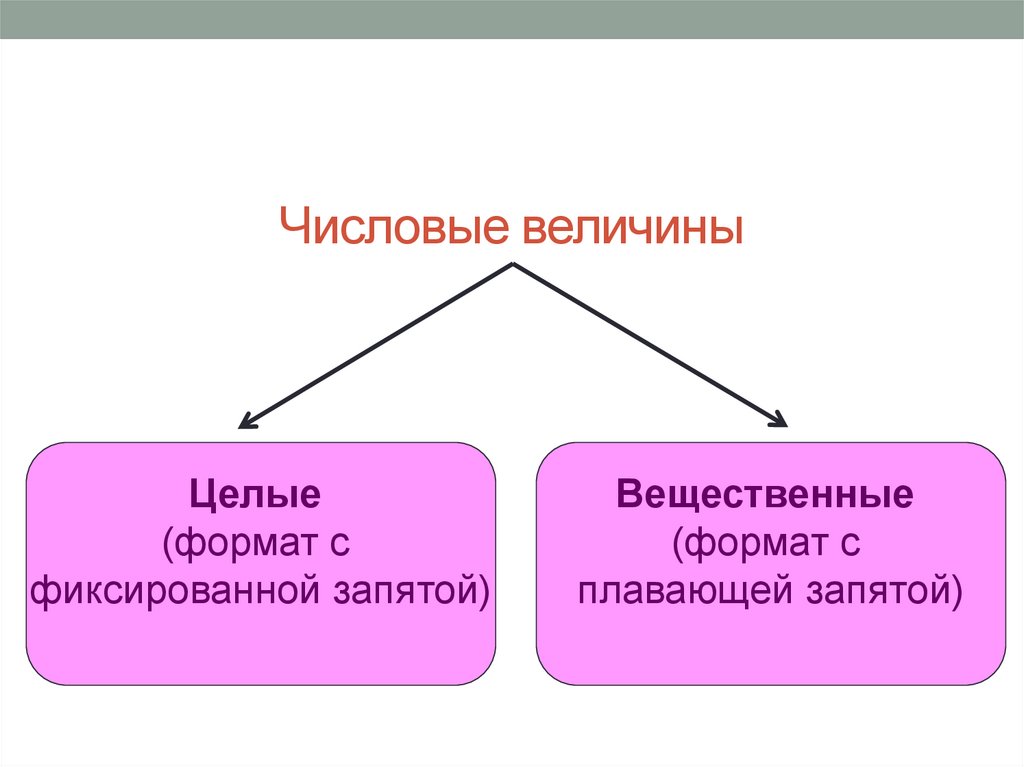
Числовые величины
Целые
(формат с
фиксированной запятой)
Вещественные
(формат с
плавающей запятой)

7.

Целые числа без знака
Целые числа без знака обычно занимают в памяти один или
два байта и принимают:
в однобайтовом формате значения от 000000002 до 111111112 ,
в двубайтовом формате — от 00000000 000000002 до 11111111
111111112.
Диапазоны значений целых чисел без знака
Формат числа в
байтах
Диапазон
Запись с
порядком
Обычная
запись
1
0 ... 28–1
0 ... 255
2
0 ... 216–1
0 ... 65535
7

8.

Целые беззнаковые числа
8
Беззнаковые данные – не могут быть отрицательными.
Байт (символ)
память: 1 байт = 8 бит
Си: unsigned char
Паскаль: byte
младший
старший
7
6
5
4
3
2
1
0
0
1
0
0
1
1
1
0
старший полубайт
старшая цифра
416
младший полубайт
младшая цифра
E16
10011102 = 4E16 = ‘N’
биты

9.

Пример 1. Для хранения целого числа без знака используется один
байт. Записать представление числа 19.
1 шаг: Переведем число 19 из десятичной системы счисления в
двоичную.
19 2
18 9
1 8
1
2
4
4
0
19 = 100112
2
2
2
0
2
1
0
1
2
0
2 шаг: Так как для представления числа в компьютере выделен 1 байт,
то код числа должен содержать 8 знаков (8 бит). Поэтому впереди числа
дописываем 3 незначащих нуля.
19 =
0
0
0
1
0
0
1
1
9

10.

Целые беззнаковые числа
10
Целое без знака
память: 2 байта = 16 бит
диапазон значений 0…65535, 0…FFFF16 = 216-1
Си: unsigned int
Паскаль: word
15 14 13 12 11 10
9
8
7
6
5
4
3
2
1
0
0 1 0 0 1 1 0 1 0 1 1 1 1 0 1 0
старший байт
младший байт
4D16
7A16
1001101011110102 = 4D7A16
Длинное целое без знака
память: 4 байта = 32 бита
диапазон значений 0…FFFFFFFF16 = 232-1
Си: *unsigned long int
Паскаль: **dword
биты

11.

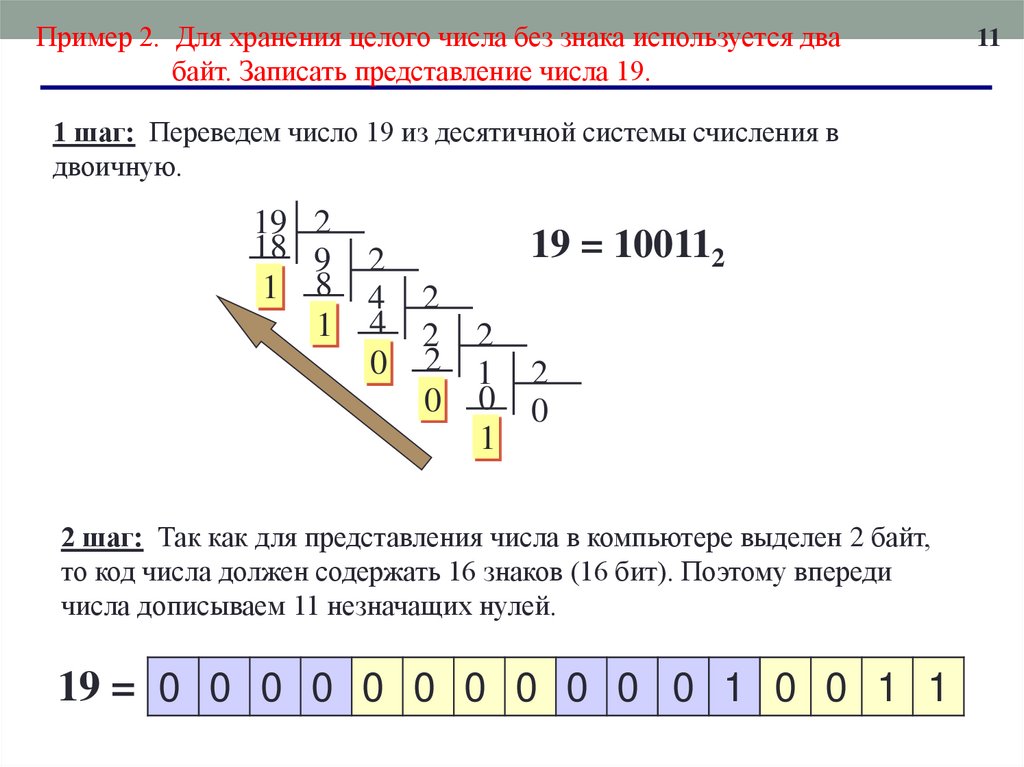
Пример 2. Для хранения целого числа без знака используется два
байт. Записать представление числа 19.
1 шаг: Переведем число 19 из десятичной системы счисления в
двоичную.
19 2
18 9
1 8
1
2
4
4
0
19 = 100112
2
2
2
0
2
1
0
1
2
0
2 шаг: Так как для представления числа в компьютере выделен 2 байт,
то код числа должен содержать 16 знаков (16 бит). Поэтому впереди
числа дописываем 11 незначащих нулей.
19 = 0 0 0 0 0 0 0 0 0 0 0 1 0 0 1 1
11

12.

Целые числа со знаком
Целые числа со знаком обычно занимают в памяти компьютера
один, два или четыре байта, при этом самый левый (старший)
разряд содержит информацию о знаке числа. Знак “плюс”
кодируется нулем, а “минус” — единицей.
Диапазоны значений целых чисел без знака
Формат числа в байтах
Диапазон
Запись с порядком Обычная запись
1
-27 ... 27–1
-128 ... 127
2
-215 ... 215–1
-32768 ... 32767
4
-231…231-1
-2147483648 ...
2147483647
12

13.

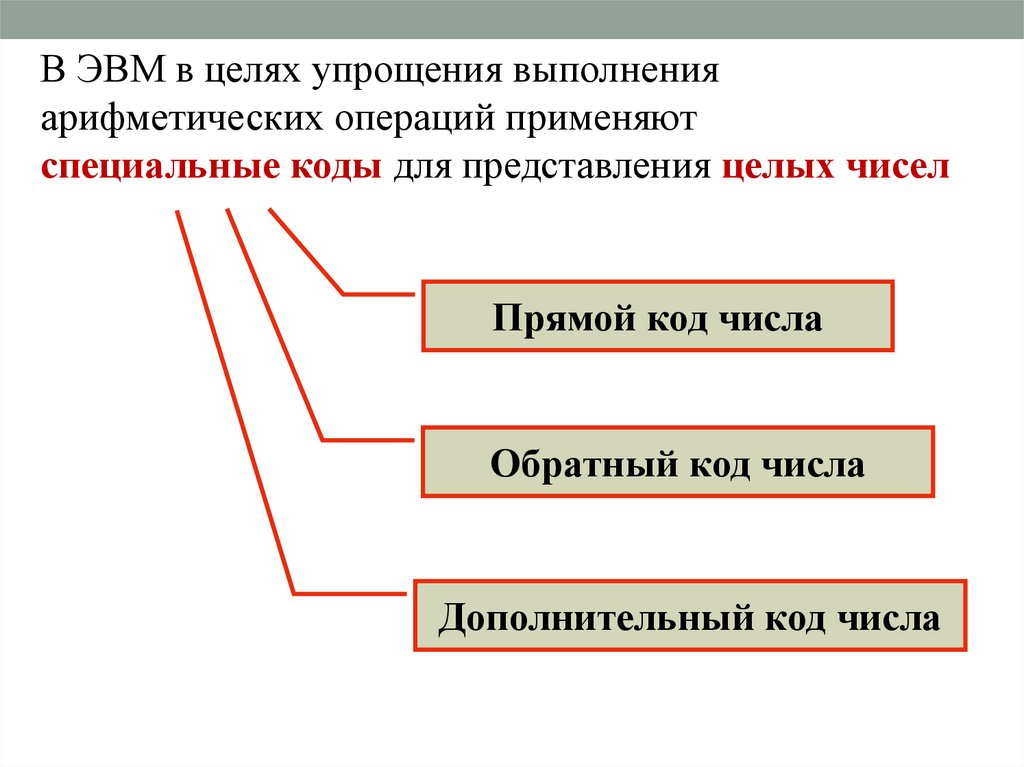
В ЭВМ в целях упрощения выполнения
арифметических операций применяют
специальные коды для представления целых чисел
Прямой код числа
Обратный код числа
Дополнительный код числа

14.

В компьютерной технике применяются три формы записи
(кодирования) целых чисел со знаком:
прямой код, обратный код и дополнительный код.
Прямой код – чаше всего отводится 2 байта памяти (16 бит), в
старший разряд записывается «0» если число положительное и «1»
– если число отрицательное.
Обратный код – для положительных чисел совпадает с прямым
кодом, для отрицательных чисел образуется из прямого кода
заменой нулей единицами, а единиц – нулями, кроме цифр
знакового разряда.
Пример. Число -5710 = -1110012
прямой
1
0
0
0
0
0
0
0
0
0
1
1
1
0
0
1
обратный
1
1
1
1
1
1
1
1
1
1
0
0
0
1
1
0

15.

Дополнительный код используется для представления
отрицательных чисел, позволяет заменить арифметическую
операцию вычитания операцией сложения, что существенно
упрощает работу процессора и увеличивает его быстродействие.
Дополнительный код отрицательного числа А, хранящегося в n
ячейках равен 2n – │A│. Образуется из обратного кода с
последующим прибавлением единицы к его младшему разряду
1310
–1210
Прямой код
00001101
10001100
Обратный код
–
11110011
Дополнительный код
–
11110011
+
1
11110100

16.

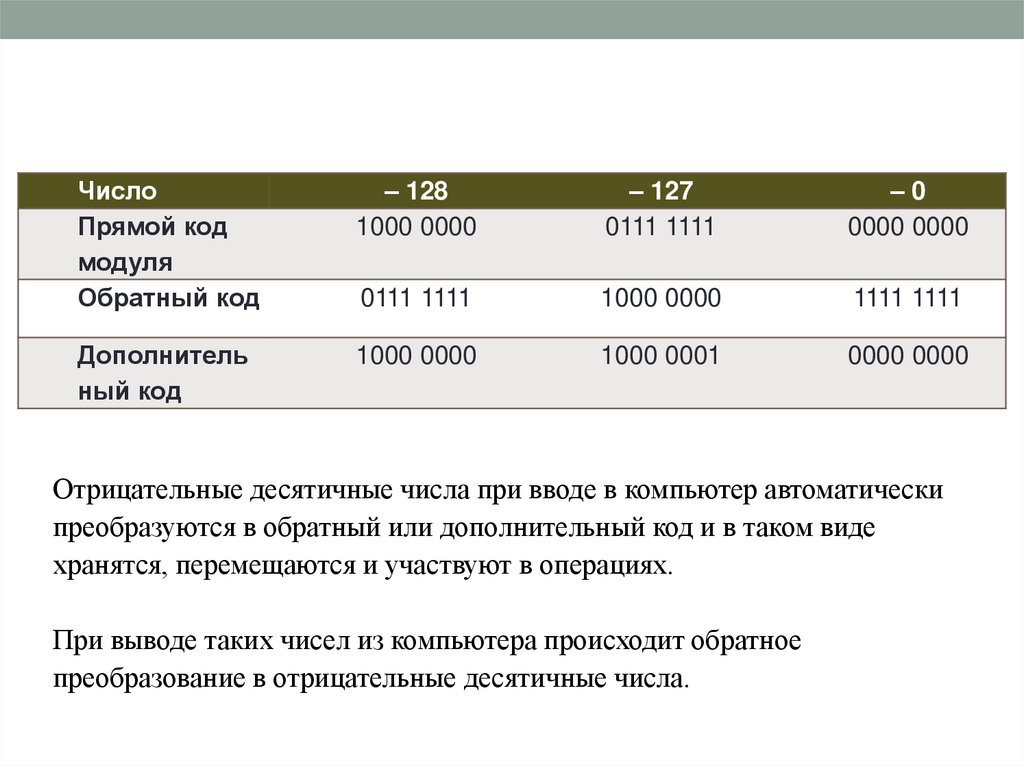
Число
Прямой код
модуля
Обратный код
– 128
1000 0000
– 127
0111 1111
–0
0000 0000
0111 1111
1000 0000
1111 1111
Дополнитель
ный код
1000 0000
1000 0001
0000 0000
Отрицательные десятичные числа при вводе в компьютер автоматически
преобразуются в обратный или дополнительный код и в таком виде
хранятся, перемещаются и участвуют в операциях.
При выводе таких чисел из компьютера происходит обратное
преобразование в отрицательные десятичные числа.

17.

Определим диапазон чисел, которые могут храниться в оперативной
памяти в формате длинных целых чисел со знаком (отводится 32 бита
памяти): минимальное число –231 = –214748364810
максимальное число 231 – 1 = 214748364710
Разрядность
Минимум
(без знака)
Максимум
(без знака)
Минимум
(со знаком)
Максимум
(со знаком)
8
0
16
0
32
0
255
65535
4294967295
–128
–32768
–2147483648
127
32767
2147483647
– простота и наглядность представления чисел, простота алгоритмов
реализации арифметических операций
– небольшой диапазон представляемых чисел, недостаточный для решения
большинства прикладных задач

18.

Примеры
Пример. Число –7210 = –10010002 в однобайтовом формате
1
1
0
0
1
0
0
0
Пример. Число 6210 = 1111102 в однобайтовом формате
0
0
1
1
1
1
1
0

19.

Задание.
Записать представление чисел 234 и 400 в двухбайтовом формате
для компьютера
234 =
400 =

20.

Представление вещественных чисел
в компьютере
формат с фиксированной запятой – целые числа
формат с плавающей запятой – вещественные числа
Вещественные числа хранятся и обрабатываются в компьютере в формате с
плавающей запятой. В этом случае положение запятой в записи числа может
изменяться.
Формат чисел с плавающей запятой базируется на экспоненциальной форме
записи, в которой может быть представлено любое число.
Формат числа
Диапазон абсолютных
значений
Биты мантиссы
Размер в
байтах
(битах)
10-45 … 1038
10-39 … 1038
10-324 … 10308
10-4932 … 104932
23+1
используется редко
52+1
64+1
4 (32)
6 (48)
8 (64)
10 (80)
одинарный
вещественный
двойной
расширенный
Пример. Число 7210 = 10010002 в однобайтовом формате
0
1
0
0
1
0
0
0

21.

ЭКСПОНЕНЦИАЛЬНАЯ ФОРМА ЗАПИСИ ЧИСЛА
Любое число A в системе счисления с основанием q можно записать
в виде A = m ∙ qn, где m называется мантиссой числа, а n – порядком
числа.
Такой способ записи чисел называется представлением числа с
плавающей точкой.
Примеры
345,67 = 34567 10-2
345,67 = 3,4567 102
345,67 = 0,34567 103

22.

Способ представления числа с плавающей запятой, опирается на нормализованную
(экспоненциальную) запись действительных чисел.
Определение. Нормализованной называется запись отличного от нуля
действительного числа в виде m• qn, где q – целое число (положительное,
отрицательное или ноль), а m – правильная P-ричная дробь, у которой первая
цифра после запятой не равна нулю, т. е. 1/P≤m<1. При этом m называется
мантиссой числа, q – порядком числа.
Пример:
порядок n=2.
0,0836= 0,836*102, здесь нормализованная мантисса: m=0,836,
ненормализованное число
нормализованное число

23.

Вещественные числа
Например, 123,45 = 0,12345 · 103
Порядок указывает, на какое количество позиций и в каком
направлении должна сместиться десятичная запятая в мантиссе.
Число в формате с плавающей запятой может занимать в памяти 4
байта (обычная точность) или 8 байтов (двойная точность).
При записи числа выделяются разряды для хранения знака
мантиссы, знака порядка, порядка и мантиссы.
*Мантисса M и порядок n определяют диапазон изменения чисел
и их точность.

24.

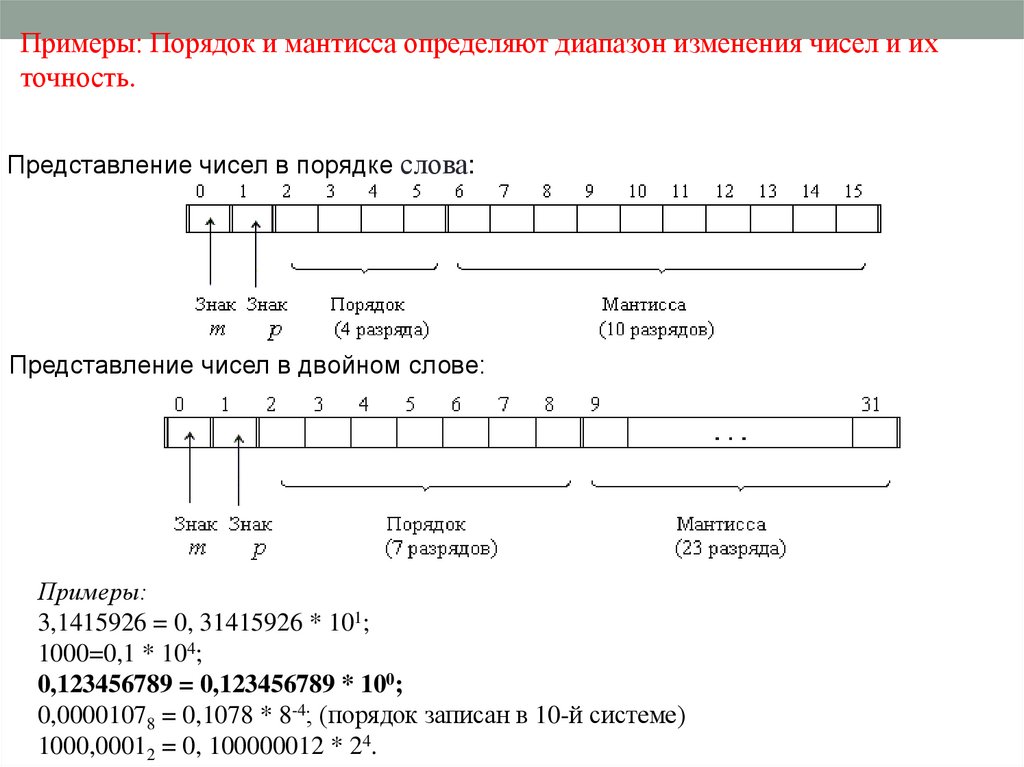
Примеры: Порядок и мантисса определяют диапазон изменения чисел и их
точность.
Представление чисел в порядке слова:
Представление чисел в двойном слове:
Примеры:
3,1415926 = 0, 31415926 * 101;
1000=0,1 * 104;
0,123456789 = 0,123456789 * 100;
0,00001078 = 0,1078 * 8-4; (порядок записан в 10-й системе)
1000,00012 = 0, 100000012 * 24.

25.

Определим максимальное число и его точность для
формата чисел обычной точности
• Для хранения порядка и его знака отводится 8
разрядов, а для хранения мантиссы и ее знака – 24
разряда:
01 1 1 1 1 1 1 01 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
знак и порядок
знак
и
мантисса

26.

Определим максимальное число и его точность для
формата чисел обычной точности
Максимальное значение порядка числа составит 11111112 = 12710, и,
следовательно, максимальное значение числа составит:
2127 = 1,7014118346046923173168730371588 · 1038.
Максимальное значение положительной мантиссы равно:
223 – 1 ≈ 223 = 2(10*2,3) ≈ 10002,3 = 10(3 · 2,3) ≈ 107.
Таким образом, максимальное значение чисел обычной точности вычислений
составит 1,701411·1038 (количество значащих цифр десятичного числа в данном
случае ограниченно 7 разрядами).

27.

Умножение и деление чисел с плавающей
запятой
При умножении чисел в формате с плавающей запятой
порядки складываются, а мантиссы перемножаются.
При делении из порядка делимого вычитается порядок
делителя, а мантисса делимого делится на мантиссу делителя.
Затем число обязательно нормализуется, т. е. после запятой
должна стоять цифра, отличная от нуля.
Умножение
0,1 × 25
× 0,1 × 23
______________
0,01 × 28 = 0,1 × 27
Деление
0,1 × 25
: 0,1 × 23
______________
1 × 22 = 0,1 × 23

28.

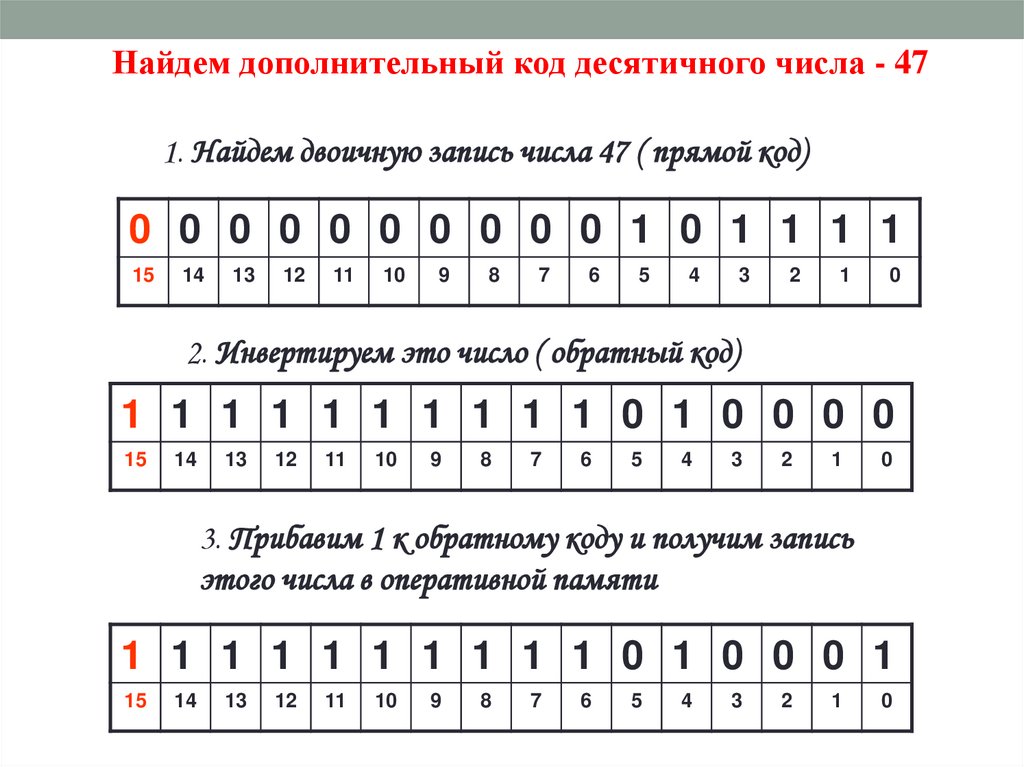
Найдем дополнительный код десятичного числа - 47
1. Найдем двоичную запись числа 47 ( прямой код)
0 0 0 0 0 0 0 0 0 0 1 0 1 1 1 1
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
2. Инвертируем это число ( обратный код)
1 1 1 1 1 1 1 1 1 1 0 1 0 0 0 0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
3. Прибавим 1 к обратному коду и получим запись
этого числа в оперативной памяти
1 1 1 1 1 1 1 1 1 1 0 1 0 0 0 1
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0

29.

Задание 1. Записать внутреннее представление следующих десятичных чисел,
используя 8 – разрядную ячейку:
6410
- 12010
Прямой код
Обратный код
Дополнительный код

30.

Д/З
• 1. Представьте в восьмиразрядном формате прямые
коды десятичных чисел: 1) 64; 2) 58; 3) 72; 4) -96.