Similar presentations:
Приложения булевых алгебр к переключательным схемам
1.
Приложениябулевых алгебр к
переключательным
схемам
Михаил Новокрещёнов Александрович
Ист-212
2.
План работы:Для начала чтобы
рассмотреть главную тему
рассмотрим само понятие булева
алгебра.
Разберём её основы и двинемся
дальше
После мы рассмотрим понятие
переключательных схем и её
составляющих.
И под конец мы рассмотрим всё
вместе
А когда пройдем все эти этапы мы
напишем итог
3.
Булева алгебраБулева алгебра-это раздел алгебры, в котором значениями
переменных являются значения истинности true и false,
обычно обозначаемые 1 и 0 соответственно. (что-то знакомое
да?)
Вместо элементарной алгебры, где значениями переменных
являются числа, а простыми операциями являются сложение
и умножение, основными операциями булевой алгебры
являются конъюнкция (и), обозначаемая как ∧, дизъюнкция
(или), обозначаемая как ∨, и отрицание.
4.
Элементы булевой алгебрыОсновными элементами булевой алгебры являются:
Логические константы;
Переменные;
Операция;
Выражения;
Функции;
Законы;
Рассмотрим эти элементы по отдельности :)
Я хочу
спать
5.
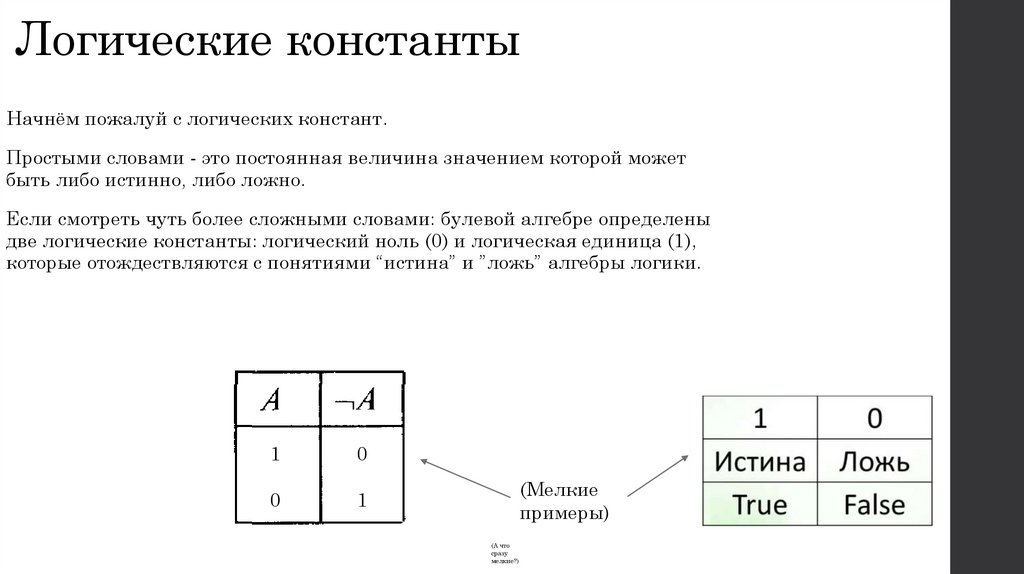
Логические константыНачнём пожалуй с логических констант.
Простыми словами - это постоянная величина значением которой может
быть либо истинно, либо ложно.
Если смотреть чуть более сложными словами: булевой алгебре определены
две логические константы: логический ноль (0) и логическая единица (1),
которые отождествляются с понятиями “истина” и ”ложь” алгебры логики.
1
0
0
1
(Мелкие
примеры)
(А что
сразу
мелкие?)
6.
ПеременныеСледующие по списку переменные и операции.
Булевы (логические, двоичные) переменные - переменные, принимающие
значения из множества {0,1}.
Операции
Основными операциями булевой алгебры являются отрицание, конъюнкция
и дизъюнкция.
Операция отрицания является унарной, а конъюнкция и дизъюнкция – nарными. Операции обозначаются следующим образом:
Отрицание
Конъюнкция
Дизъюнкция
7.
ВыраженияПомогите!
Логическим (булевым) выражением называется совокупность
булевых переменных, соединенных знаками булевых операций при
возможном наличии скобок для изменения порядка выполнения
операций. При отсутствии скобок порядок выполнения операций
определяется их приоритетом (значимостью). Для булевых
операций порядок убывания приоритета следующий:
Пример:
Ещё один
пример:
8.
ФункцииБулевой (логической) функцией называется функция, аргументами
которой являются булевы переменные, а сама функция принимает
значение из множества {0,1}.
Областью определения булевой функции является совокупность
2x двоичных наборов ее аргументов. Набор аргументов можно
рассматривать как n компонентный двоичный вектор.
Булеву функцию можно задать с помощью следующих форм:
Аналитической;
Табличной;
Графической;
Таблично-графической;
Числовой;
Символической.
9.
Аналитическая формаАналитическая форма – булева
функция задается логическим
выражением.
Например:
10.
Табличная формаТабличная форма – булева функция задается таблицей
истинности.
В качестве примера составим таблицу истинности для функции y1 :
11.
Основные законы булевой алгебрыК основным законам булевой алгебры относятся:
1. Коммутативные (переместительные) законы:
2. Ассоциативные (сочетательные) законы:
3. Дистрибутивные (распределительные) законы:
4. Закон двойного отрицания:
12.
Основные законы булевой алгебры (2):5. Законы тавтологии (идемпотентности):
6. Законы нулевого элемента:
7. Законы единичного элемента:
8. Законы дополнительного элемента:
13.
Основные законы булевой алгебры (3):9. Законы двойственности (де Моргана):
10. Законы поглощения:
11. Правила сокращения:
12.Правила склеивания:
14.
Переключательные схемыПосле рассмотрения некоторых основ булевой алгебры, мы можем
приступить к рассмотрению, переключательных схем и уже после ответить
на главный вопрос этой презентации.
Переключательная схема — это схематическое изображение некоторого
устройства, состоящего из переключателей и соединяющих их
проводников, а также из входов и выходов, на которые подаётся и с
которых снимается электрический сигнал.
(Каждый переключатель имеет только два состояния: замкнутое и разомкнутое.)
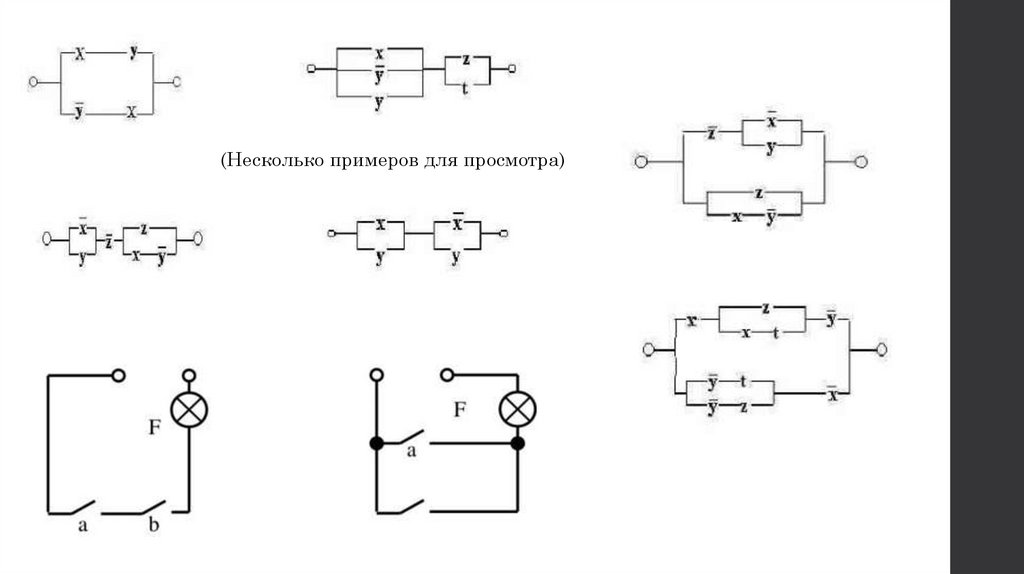
Рассмотрим несколько примеров переключательных схем:
15.
(Несколько примеров для просмотра)16.
Рассмотрим несколько схем с логическимипеременными и функцией проводимостью F:
Найдем функцию проводимости F
некоторых переключательных схем и
найдём переключательную схему по
функции проводимости F:
Y
X
Z
F(x, y, z, o) = x
z
y o
17.
Схемы• Две схемы называются равносильными, если через одну из них проходит
ток тогда и только тогда, когда он проходит через другую (при одном и
том же входном сигнале).
• Из двух равносильных схем более простой считается та схема, функция
проводимости которой содержит меньшее число логических операций
или переключателей.
Разобрав определение переключательной схемы и её некоторые виды,
разберём задачи при рассмотрении таких схем: синтез и анализ схемы.
Синтез схемы по заданным условиям ее работы сводится к следующим трём этапам 1. составлению функции проводимости по таблице истинности, отражающей эти условия;
2. упрощению этой функции;
3. построению соответствующей схемы.
Анализ схемы сводится к 1. определению значений её функции проводимости при всех возможных наборах входящих в
эту функцию переменных.
2. получению упрощённой формулы.
Разберём пару примеров:
18.
Пример:Построим схему, содержащую 4 переключателя x, y, z и t, такую, чтобы она
проводила ток тогда и только тогда, когда замкнут контакт переключателя
t и какой-нибудь из остальных трёх контактов.
Решение. В этом случае можно обойтись без построения таблицы истинности.
Очевидно, что функция проводимости имеет вид F(x, y, z, t) = t . (x v y v z).
19.
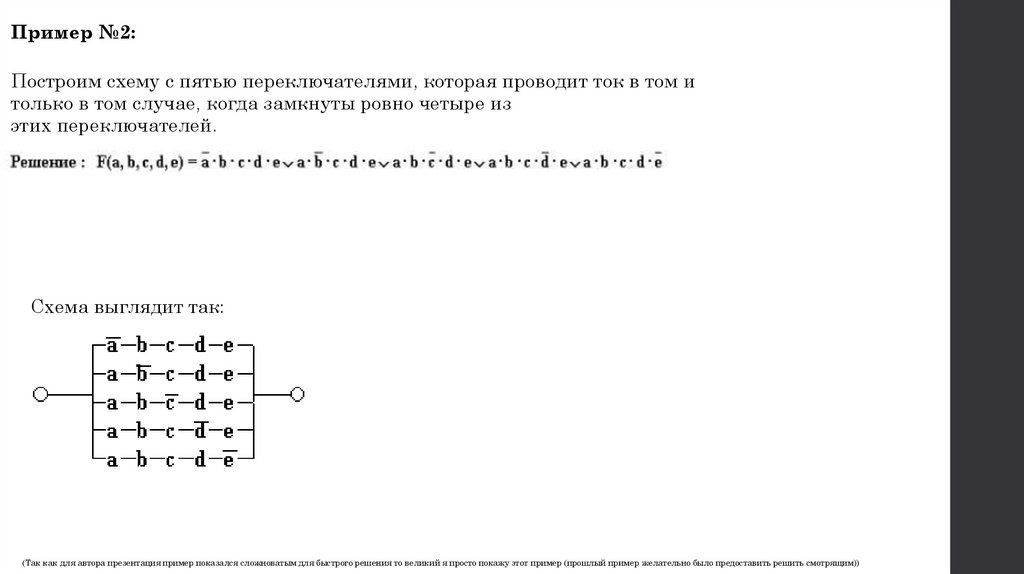
Пример №2:Построим схему с пятью переключателями, которая проводит ток в том и
только в том случае, когда замкнуты ровно четыре из
этих переключателей.
Схема выглядит так:
(Так как для автора презентация пример показался сложноватым для быстрого решения то великий я просто покажу этот пример (прошлый пример желательно было предоставить решить смотрящим))
20.
Итог:Подведём итог, сегодня мы рассмотрели приложения булевых алгебр
к переключательным схемам и поняли как булева алгебра связана с
переключательными схемами, как можно находить функции проводимости
по схемам, как находить схемы по формулам и рассмотрели сами схемы, за
это время, что мы изучали эту тему мы смогли увидеть связь булевой
алгебры и переключательных схем.

















 mathematics
mathematics








