Similar presentations:
Теорема о произведении отрезков хорд. Теорема о произведении отрезков секущих. Теорема о квадрате касательной
1.
ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ ХОРД.ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ СЕКУЩИХ.
ТЕОРЕМА О КВАДРАТЕ КАСАТЕЛЬНОЙ.
2.
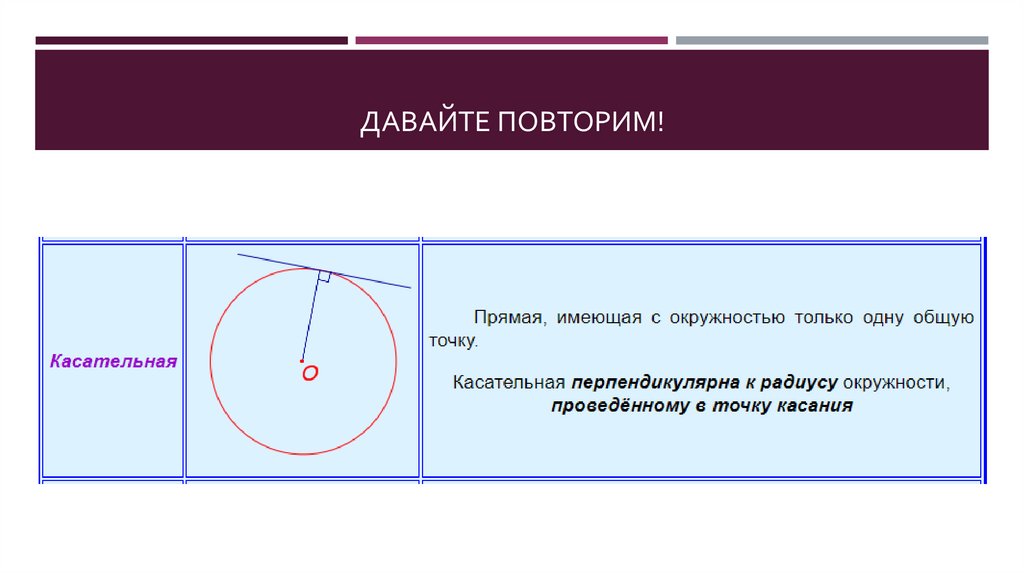
ДАВАЙТЕ ПОВТОРИМ!3.
ДАВАЙТЕ ПОВТОРИМ!4.
ДАВАЙТЕ ПОВТОРИМ!5.
ДАВАЙТЕ ПОВТОРИМ!6.
ДАВАЙТЕ ПОВТОРИМ!7.
ДАВАЙТЕ ПОВТОРИМ!8.
ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ ХОРДЕсли две хорды окружности пересекаются, то произведение отрезков одной хорды, равно
произведению отрезков другой хорды.
9.
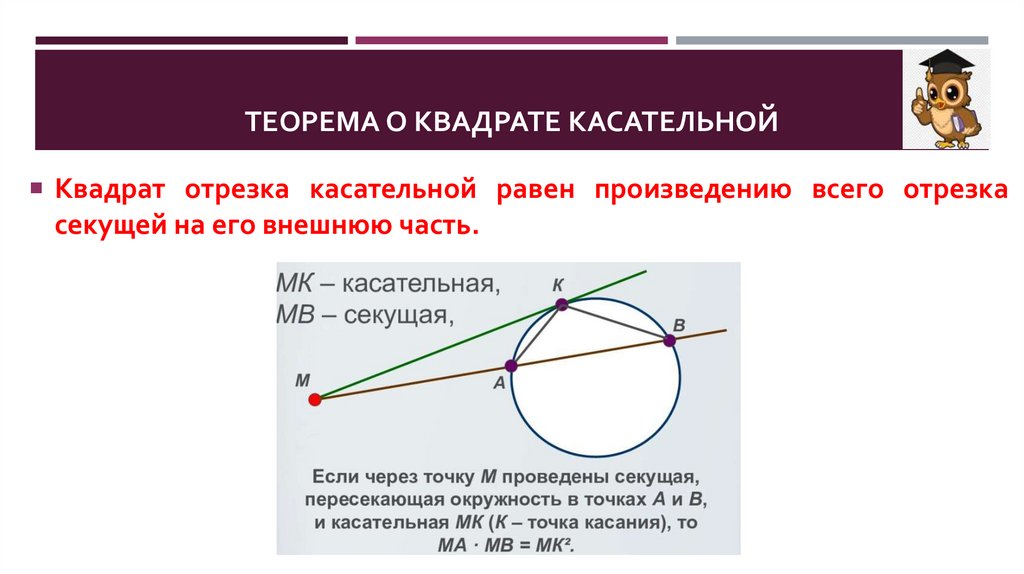
ТЕОРЕМА О КВАДРАТЕ КАСАТЕЛЬНОЙКвадрат отрезка касательной равен произведению всего отрезка
секущей на его внешнюю часть.
10.
ТЕОРЕМА О ПРОИЗВЕДЕНИИ ОТРЕЗКОВ СЕКУЩИХЕсли из точки, лежащей вне окружности, проведены две секущие, то
произведение одной секущей на её внешнюю
произведению другой секущей на её внешнюю часть.
часть
равно
11.
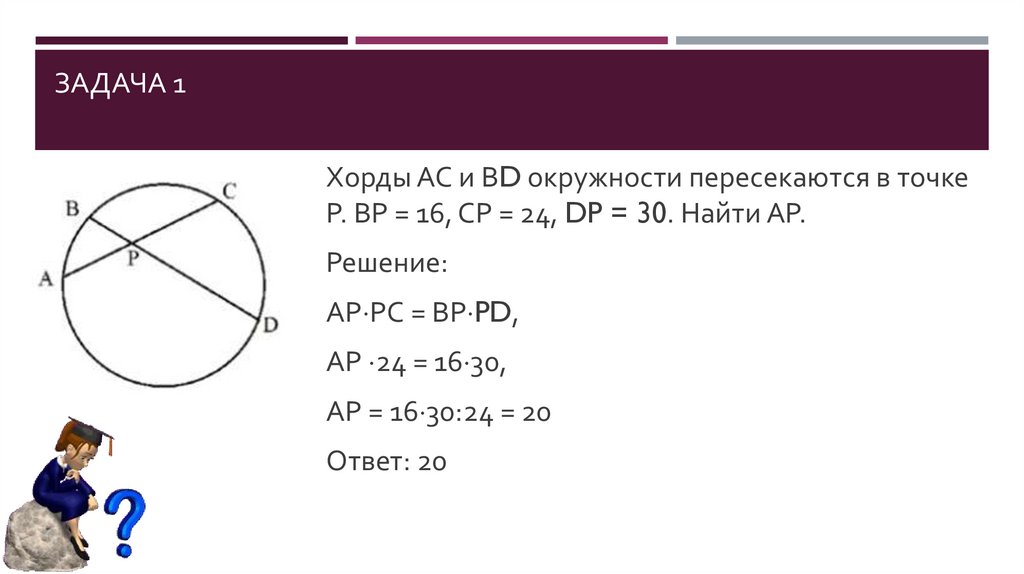
ЗАДАЧА 1Хорды АС и ВD окружности пересекаются в точке
Р. ВР = 16, СР = 24, DP = 30. Найти АР.
Решение:
АР РС = ВР PD,
АР 24 = 16 30,
АР = 16 30:24 = 20
Ответ: 20
12.
ЗАДАЧА 2Через точку A, лежащую вне окружности,
проведены две прямые. Одна прямая касается
окружности в точке K. Другая прямая пересекает
окружность в точках B и C, причём AB = 5, AC = 20.
Найдите AK.
Решение:
АК2 = АВ АС,
АК2 = 5 20 = 100,
АК = 10
Ответ: 10
13.
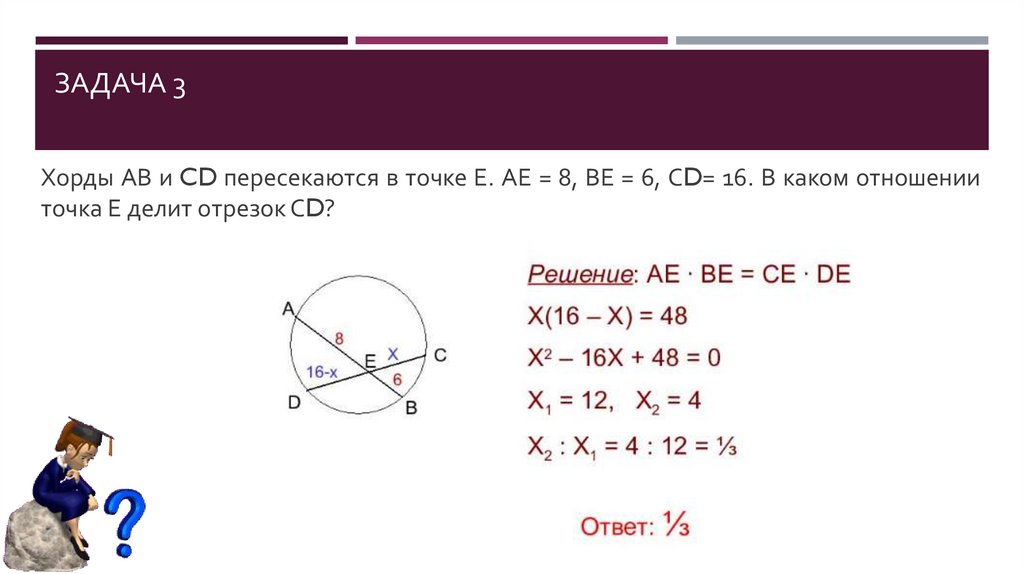
ЗАДАЧА 3Хорды АВ и CD пересекаются в точке Е. АЕ = 8, ВЕ = 6, СD= 16. В каком отношении
точка Е делит отрезок СD?
14.
ЗАДАЧА 4Из точки вне окружности проведена секущая, пересекающая окружность в
точках, удаленных от данной на 12 и 20. Расстояние от данной точки до
центра окружности 17. Найдите радиус окружности.
Дано: АВ = 12, АС = 20, АО = 17.
Найти: ДО = ОЕ.
Решение.
АВ АС = АD AE
АВ АС = (AO – DO)(AO + EO), АВ АС = (AO – r)(AO + r)
АВ АС = AO2 – r2
12 20 = 172 - r2
r2 = 289 – 240, r2 = 47
r1 = 7, r2 = -7 – не уд.
Ответ: 7
15.
ДАВАЙТЕ ЗАКРЕПИМОтвет: 6
Ответ: 9
Ответ: 6











 mathematics
mathematics








