Similar presentations:
Касательная, хорда, секущая, радиус
1.
Подготовка к ОГЭЗадние №10
Тема:
«Касательная,хорда,секущая,
радиус.»
Источник:https://oge.sdamgia.ru/?redir=1
2.
Повторим теоремы по этой теме.1.Угол между касательной и хордой,проходящей через
точку касания,измеряется половиной заключённой в нём
дуги.
D
B
α
C
A
C₁
3.
2.Произведение отрезков одной из двухпересекающихся хорд равно произведению
отрезков другой хорды.
C
E
A
D
B
4.
3.Угол между двумя пересекающимися хордамиизмеряется суммой заключенной между ними дуг.
B
K
A
M
D
C
L
5.
4.Угол между двумя секущими,проведенными из
.
одной точки ,измеряется полуразностью
заключенных между ними дуг.
Q
B
M
P
A
6.
5.Угол между касательной и секущей,проведенными из одной точки ,измеряется
полуразностью заключенных внутри него дуг.
K
1
M
)
B
2
A
7.
6. Угол между двумя касательными ,проведеннымииз одной точки ,равен 180⁰ минус величина
заключенной внутри него дуги,меньшей
полуокружности.
K
M
)
L
8.
Найти: MN=?М
О
15
30⁰
H
₍
K
Проведем прямую от точки М в точку N.
N
Ответ:MN=15.
∠MKO= 30⁰ , ∠ MKO= 90⁰ =› ∠ HMK = 60⁰
∠ HKN = ∠MKH = 60⁰
∠KMH=∠MKN=60⁰=›∠HNK=180⁰(KMH+MKN)=60⁰
Из этого сделаем вывод,что ▲ MNKравносторонний =›
MK=MN=15.
9.
Задача 2.Дано : ON=15
M
12
N
15
Найти: MN=?
О
Ответ:MN=9
Рассмотрим ▲ MON
∠ OMN= 90⁰=› ▲ MONпрямоугольный
ON- гипотенуза
MO-катет
Найдем MN:
MN= ON²-OM²= √225-√144 =√81=9
10.
Задача 3Дано: OM=ON=10
MN=16
M
10
O
10
}
K
N
Ответ:OK=4
Найти:OK=?
16
Рассмотрим ▲ MON
OM=ON=10(по условию)
=> ▲MON- равнобедренный
OK-медиана проведенная к основанию
=>
что NK=KN=8
Рассмотрим ▲ OKM:
т.к OK-медиана проведенная к
основанию,то она еще и высота=>
∠OKM=90⁰=>▲OKM- прямоугольный;
MO-биссектриса =10
KM-катет=8
Найдем OK:
OK= OM²-MK²= √100-√64=√16=4
11.
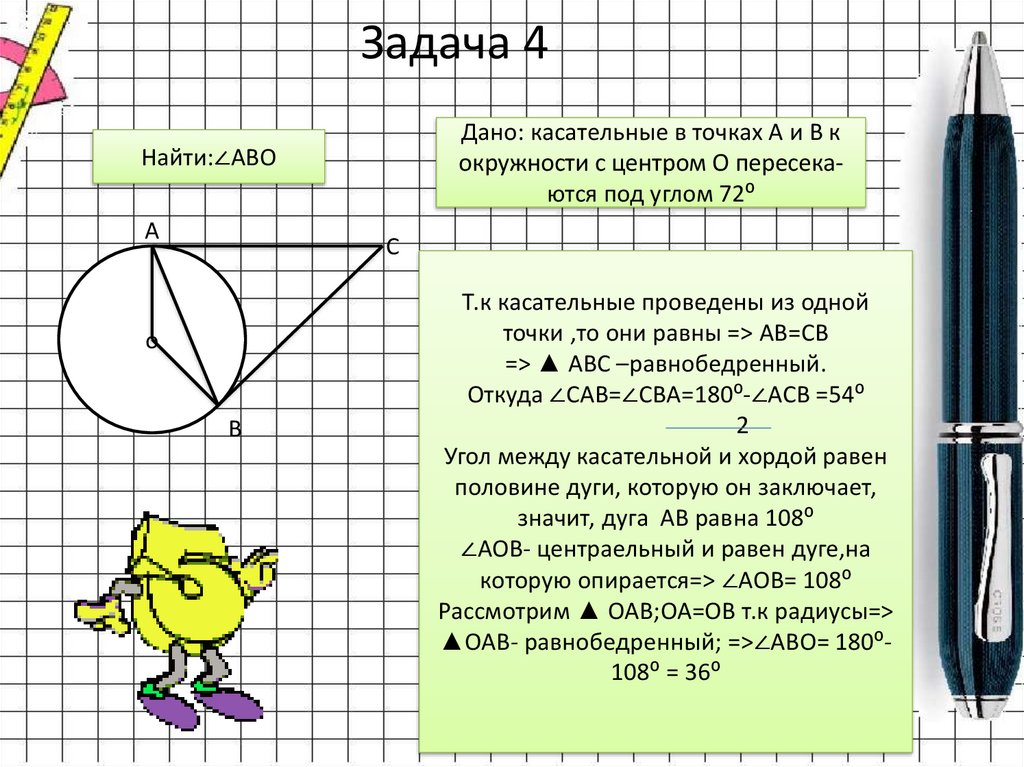
Задача 4Дано: касательные в точках A и B к
окружности с центром O пересекаются под углом 72⁰
Найти:∠ABO
А
С
о
В
Т.к касательные проведены из одной
точки ,то они равны => AB=CB
=> ▲ ABC –равнобедренный.
Откуда ∠CAB=∠CBA=180⁰-∠ACB =54⁰
2
Угол между касательной и хордой равен
половине дуги, которую он заключает,
значит, дуга AB равна 108⁰
∠AOB- центраельный и равен дуге,на
которую опирается=> ∠AOB= 108⁰
Рассмотрим ▲ OAB;OA=OB т.к радиусы=>
▲OAB- равнобедренный; =>∠ABO= 180⁰108⁰ = 36⁰
12.
Задача 5Найдите величину (в градусах ) угла α, опирающегося на
хорду AB ,равную градусу окружности.
Решение:
С
Проведем радиусы OA и OB.
а
О
А
В
Ответ:∠ ACB= 30⁰
Так как по условию задачи хорда AB равна
радиусу, то треугольник AOB — равносторонний, следовательно, все его углы
равны 60°. ∠AOB — центральный и равен
60° Угол ACB — вписанный и опирается на
ту же дугу, что и ∠ AOB. Таким образом, ∠
ACB= 60⁰:2=30⁰
13.
Задача 6Радиус OB окружности с центром в точке O пересекает хорду AC в
точке D и перпендикулярен ей. Найдите длину хорды AC, если BD = 1
см, а радиус окружности равен 5 см.
A
O
B
D
C
Найдем отрезок DO:
DO = OB − BD = 5 − 1 = 4.
Так как OB перпендикулярен AC, треугольник
AOD — прямоугольный. По теореме Пифагора имеем: AD=√AO²-√OD²=√25-√16=3 .
Треугольник AOC — равнобедренный так
как AO = OC = r, тогда AD = DC. Таким образом, AC = AD·2 = 6.
14.
Задача 7К окружности с центром в точке O проведены касательная AB и
секущая AO . Найдите радиус окружности, если , AB=21,AO=75 .
O
A
B
Соединим отрезком точки O и B; полученный отрезок — радиус, проведённый в
точку касания, поэтому OB перпендикулярен AB. Задача сводится к нахождению катета OB прямоугольного треугольника
AOB: по теореме Пифагора равен:
√75²-√21²=72
15.
Задача 8Сторона AC треугольника ABC проходит через центр описанной
около него окружности. Найдите ∠C , если ∠A = 44. Ответ дайте в
градусах.
B
A
O
D
Решение.
Угол ABC − прямой, так как он вписанный и опирается на диаметр. Следовательно треугольник ABC − прямоугольный, а ∠C=90-44=46
Ответ: 46.














 mathematics
mathematics








