Окружности. Свойства касательных хорд и секущих

1.

ЭЛЕКТИВНЫЙ КУРС В 10 КЛАССЕ
Тема: «Окружности. Свойства
касательных хорд и секущих.
Учитель: Погорелова Н.Г.
2010-2011уч.год.

2.

Тема : «Окружности. Свойства касательных
хорд и секущих.
Цели:
- Обобщить и систематизировать знания
учащихся по теме: «Окружность»;
- Познакомить учащихся с методами и
приемами решения задач;
- Сформировать умение применить
полученные знание при решении
нестандартных задач.

3.

ПОВТОРЕНИЕ
А
N
В
.
О
а
M
C
N
•АВ – хорда
MN – секущая
а - касательная к
окружности
K
.
О
М
L
•< COK – центральный угол
< NML – вписанный в
окружность угол.

4.

M
O
Свойства касательных, хорд и секущих
• Отрезки касательных
от точки А до точек касания
A
равны;
N
• Прямая,
проходящая через центр
окружности и заданную точку, делит
угол между касательными пополам
• Квадрат длины отрезка касательной равен произведению длины
секущей на длину ее внешней части:
MA 2 AN AK

5.

M
O
F
.
A
N
C
K
Q
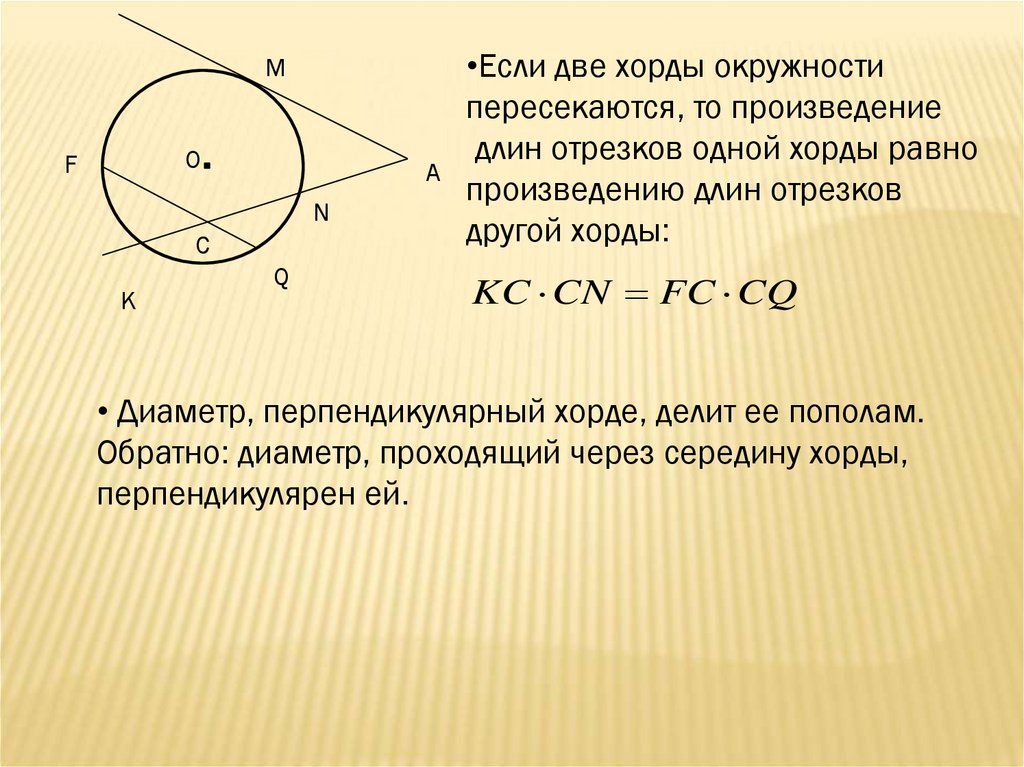
•Если две хорды окружности
пересекаются, то произведение
длин отрезков одной хорды равно
произведению длин отрезков
другой хорды:
KC CN FC CQ
• Диаметр, перпендикулярный хорде, делит ее пополам.
Обратно: диаметр, проходящий через середину хорды,
перпендикулярен ей.

6.

N1
M1
•Если из точки А, взятой вне
окружности, проведены две секущие
, то AN и AN
А
AN1 AM1 AN2 AM 2 , где AM и AM
-внешние части секущих
1
.
2
1
M2
2
N2
• Если в окружности радиуса R,
вписанный
N
угол, опирающий на хорду длины а,
равен а,
то а = 2R*sina
1
• Вписанные углы, опирающиеся на одну и ту же дугу
окружности, равны. Их градусная мера равна половине
градусной меры дуги, на которую они опираются.

7.

•Вписанный угол, опирающийся на диаметр, является
прямым.
c
a
.
b
• Угол, между пересекающимися
хордами :
a b
c
2
•Угол между секущими,
пересекающимися вне окружности:
a
c
.
b
b a
c
2

8.

• Угол между касательной и
b a
секущей:
с
a
c
b
2
• Угол между касательными:
b a
c
a
2
a
с
b
• Угол между касательной и хордой
a
c
2
с
а