Similar presentations:
Теория графов. Основные понятия
1.
ТЕОРИЯ ГРАФОВТЕМА: ОСНОВНЫЕ ПОНЯТИЯ
1
ТЕОРИИ ГРАФОВ
2.
ОСНОВНЫЕ ПОНЯТИЯТермин впервые появился 1936 г.
Венгерский математик Денеш Кёниг
(21 сентября 1884 – 19 октября 1944)
2
3.
34.
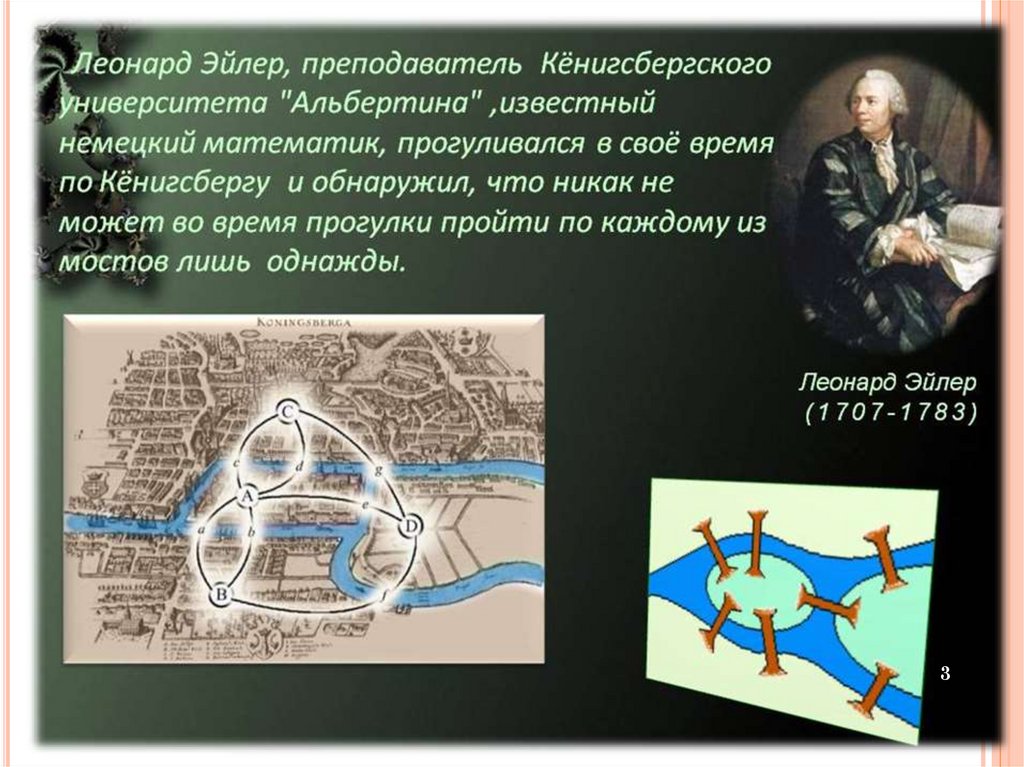
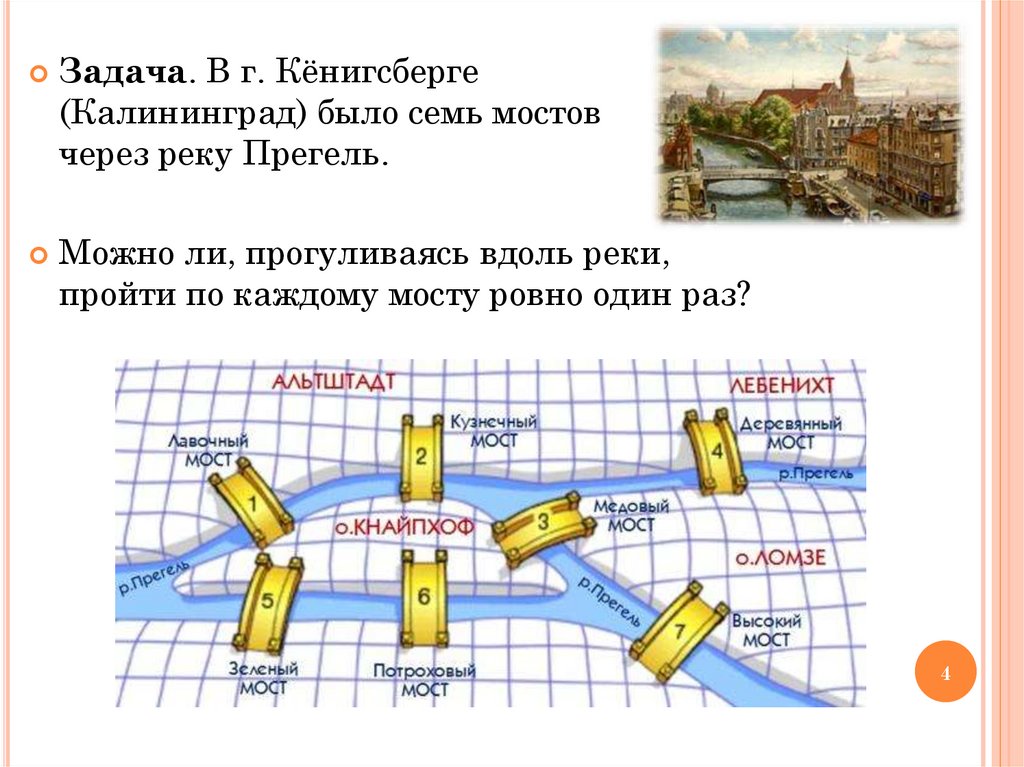
Задача. В г. Кёнигсберге(Калининград) было семь мостов
через реку Прегель.
Можно ли, прогуливаясь вдоль реки,
пройти по каждому мосту ровно один раз?
4
5.
Задача о трех домах и трехколодцах (1930 г.)
На хуторе три дома и три колодца.
Требуется провести от каждого
дома к каждому колодцу тропинку
так,
чтобы
тропинки
не
пересекались.
Польский математик
Казимир Куратовский
(1896-1980)
5
6.
67.
Пусть V – непустое множество,V(2) – множество всех его двухэлементных
подмножеств.
Определение
Пара (V , E ) , где E V ( 2) называется графом.
Элементы множества V называются вершинами
графа.
Элементы множества E называются ребрами
графа.
Обозначения: множество вершин – VG,
множество ребер – EG.
7
8.
ОпределениеЧисло вершин графа G называется
порядком графа - |G|;
Если |VG|=n, |EG|=m, то граф G
называется (n,m)-графом.
8
9.
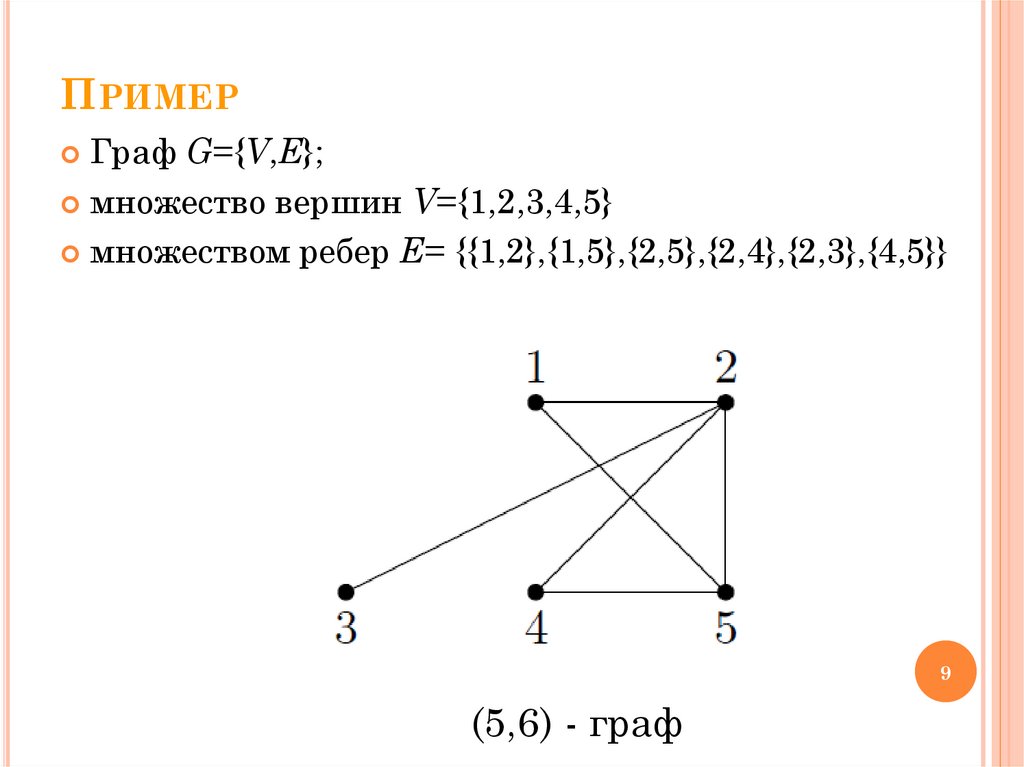
ПРИМЕРГраф G={V,E};
множество вершин V={1,2,3,4,5}
множеством ребер E= {{1,2},{1,5},{2,5},{2,4},{2,3},{4,5}}
9
(5,6) - граф
10.
ОпределениеВершины u и v графа
называются смежными,
если множество {u,v}
является ребром графа.
В этом случае u и v – концы ребра {u,v}
10
11.
ОпределениеРебра графа называются смежными,
если они имеют общий конец.
11
12.
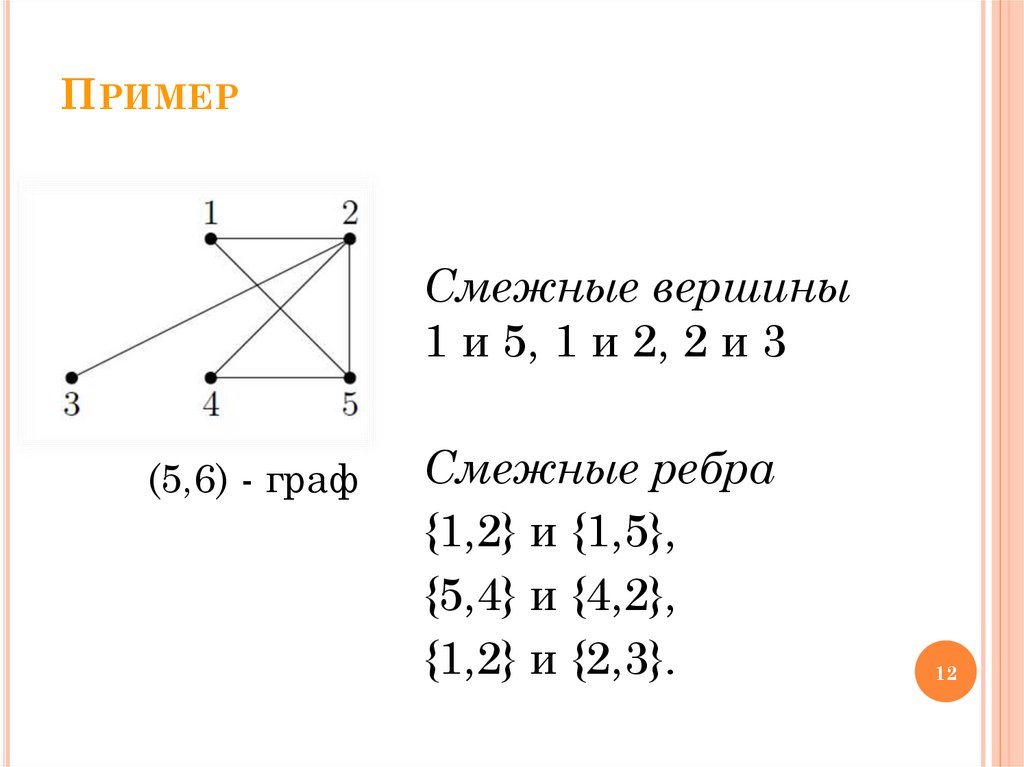
ПРИМЕРСмежные вершины
1 и 5, 1 и 2, 2 и 3
(5,6) - граф
Смежные ребра
{1,2} и {1,5},
{5,4} и {4,2},
{1,2} и {2,3}.
12
13.
ОпределениеВершина v и ребро e
называются инцидентными,
если v является концом ребра e (т.е. e={u,v}).
13
14.
ОпределениеМножество всех вершин графа,
смежных с вершиной v,
называется окружением вершины v
и обозначается N(v).
14
15.
ОпределениеКоличество всех вершин графа
в окружении вершины v
называется степенью вершины v
и обозначается deg v =|N(v)|.
15
16.
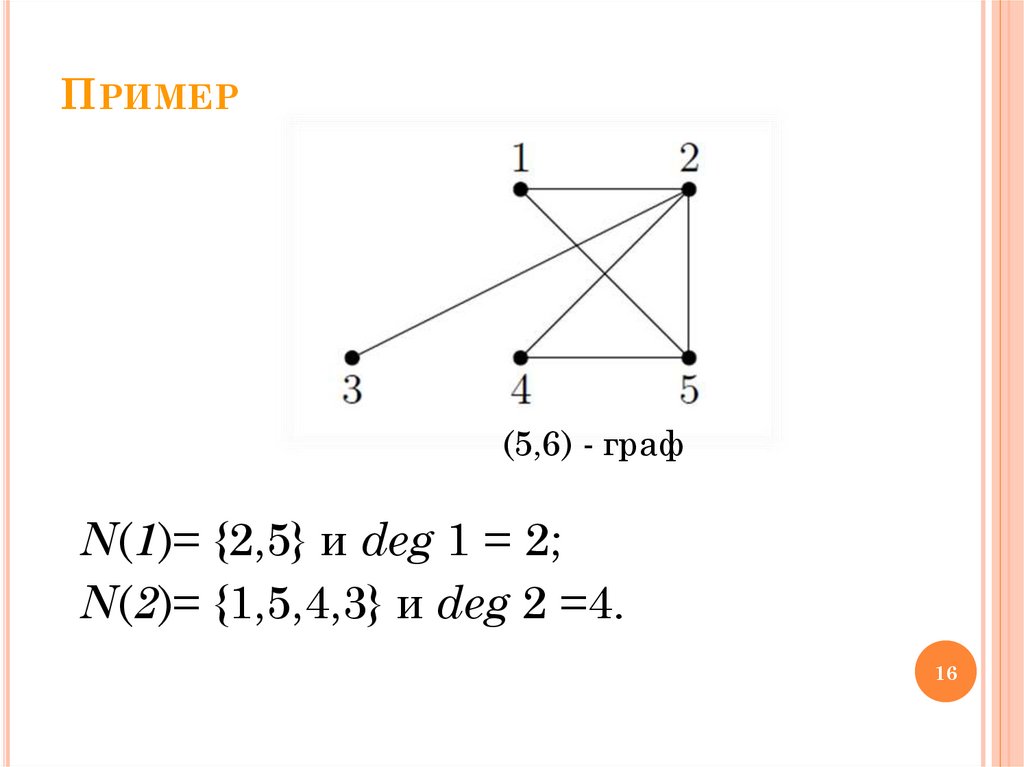
ПРИМЕР(5,6) - граф
N(1)= {2,5} и deg 1 = 2;
N(2)= {1,5,4,3} и deg 2 =4.
16
17.
НЕКОТОРЫЕ ВИДЫ ГРАФОВОпределение
Граф называется пустым,
если в нем нет ребер.
On – пустой граф порядка n (n-вершин).
1
2
3
17
18.
ОпределениеГраф называется полным,
если любые две его вершины смежны,
т.е. E= V(2).
Kn – полный граф порядка n (n-вершин).
18
19.
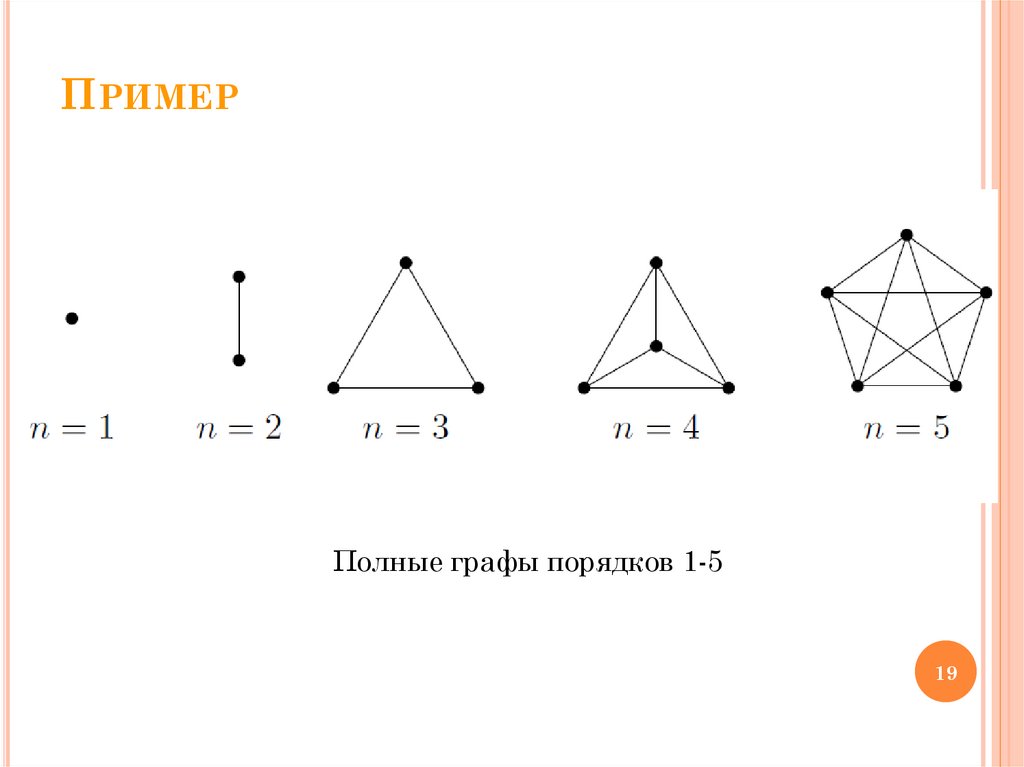
ПРИМЕРПолные графы порядков 1-5
19
20.
ОпределениеГраф называется двудольным, если
существует такое разбиение множества
вершин этого графа на две доли (два блока),
при котором концы каждого ребра
принадлежат разным долям.
Если любые две вершины в разных долях
смежны, то граф называется полным
двудольным графом и обозначается Kp,q ,
где p и q – количество вершин графа в долях.
20
21.
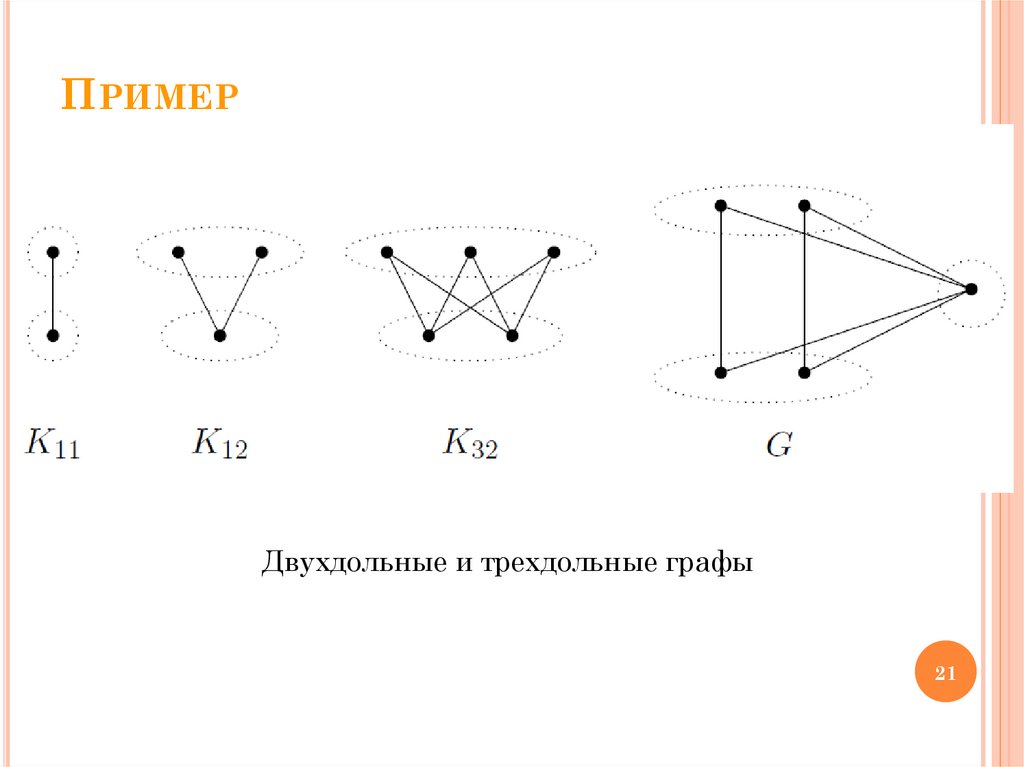
ПРИМЕРДвухдольные и трехдольные графы
21
22.
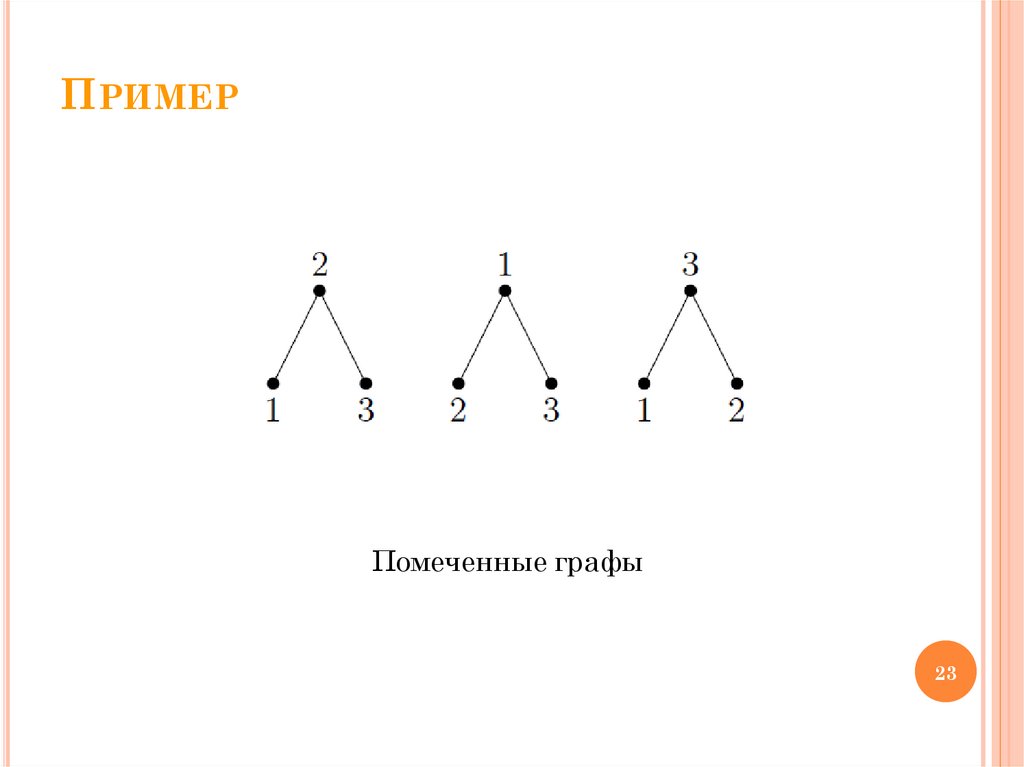
ОпределениеГраф называется помеченным,
если всем его вершинам присвоены
некоторые метки,
например, номера 1,2, …,n.
22
23.
ПРИМЕРПомеченные графы
23
24.
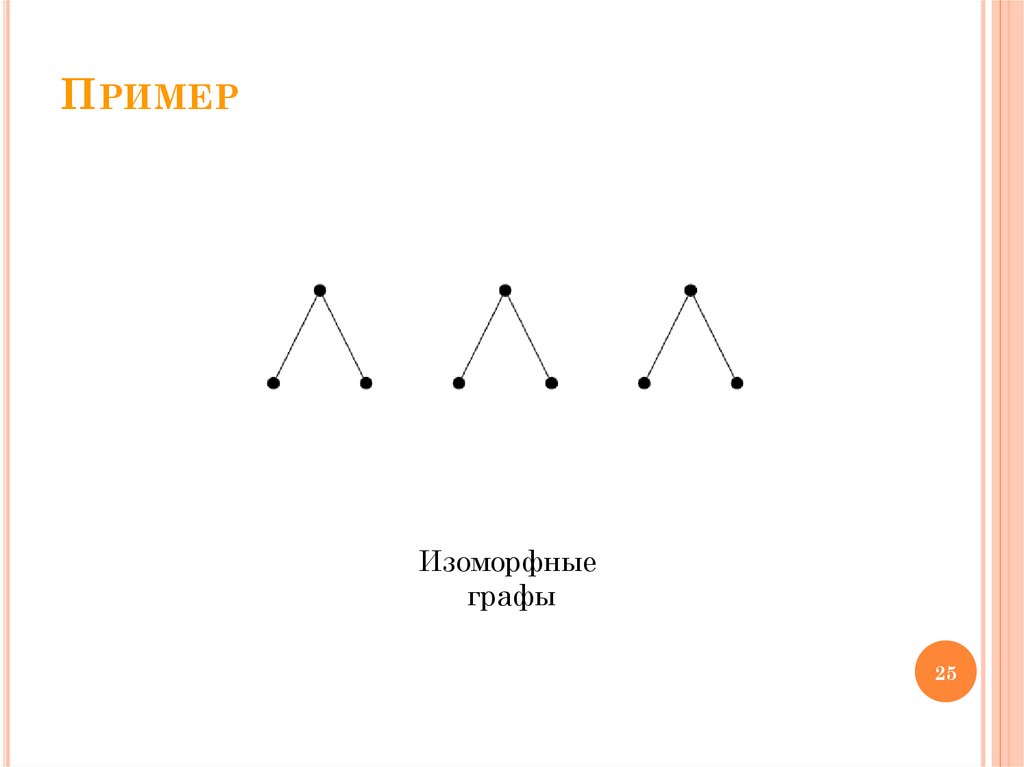
ОпределениеГрафы G и H называются изоморфными,
если существует взаимно-однозначное
отображение φ множества VG
на множество VH,
при котором вершины φ(u) и φ(v) смежны
в H тогда и только тогда, когда вершины u и v
смежны в G.
24
25.
ПРИМЕРИзоморфные
графы
25
26.
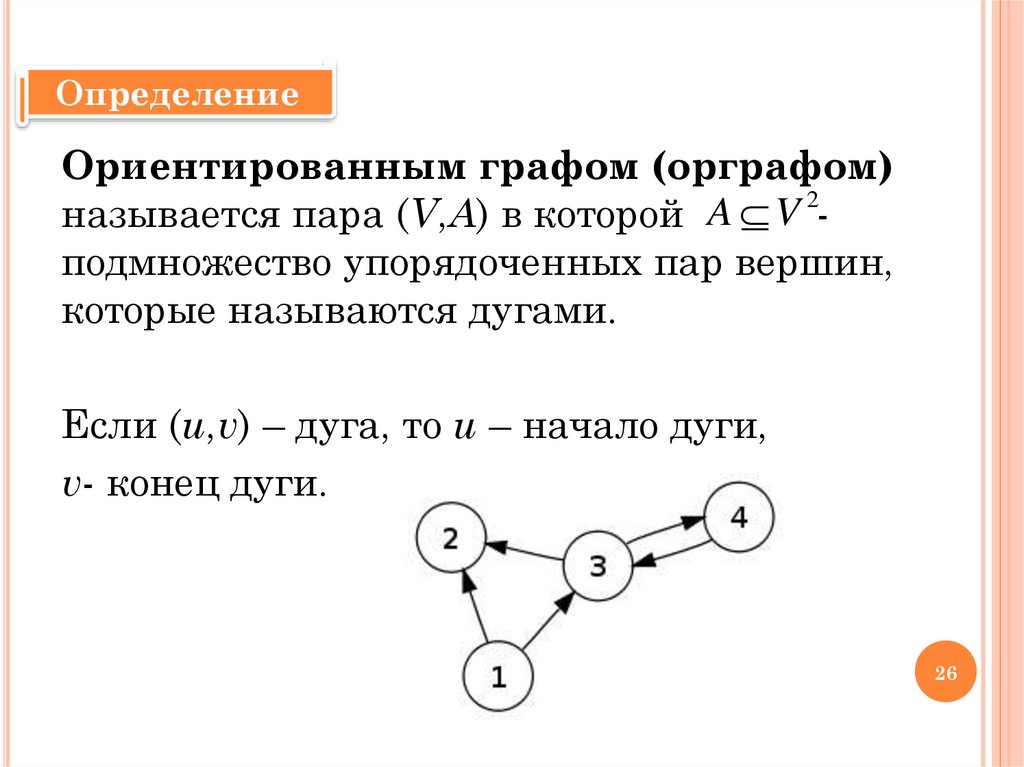
ОпределениеОриентированным графом (орграфом)
2
A
V
называется пара (V,A) в которой
подмножество упорядоченных пар вершин,
которые называются дугами.
Если (u,v) – дуга, то u – начало дуги,
v- конец дуги.
26
27.
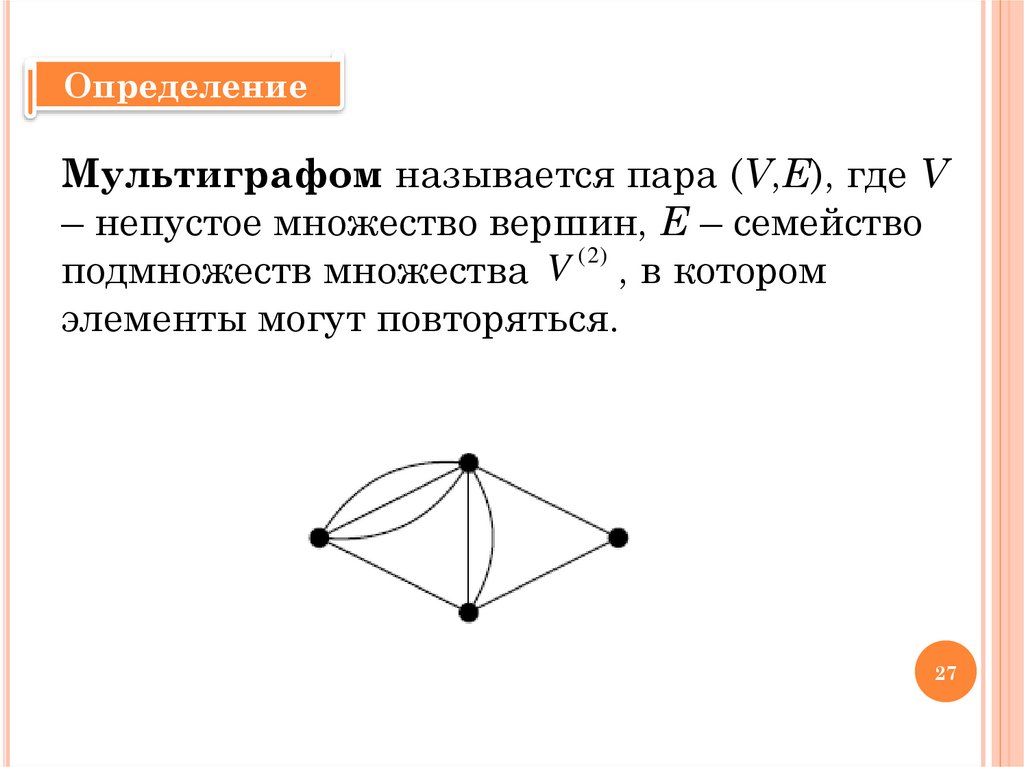
ОпределениеМультиграфом называется пара (V,E), где V
– непустое множество вершин, E – семейство
( 2)
подмножеств множества V , в котором
элементы могут повторяться.
27
28.
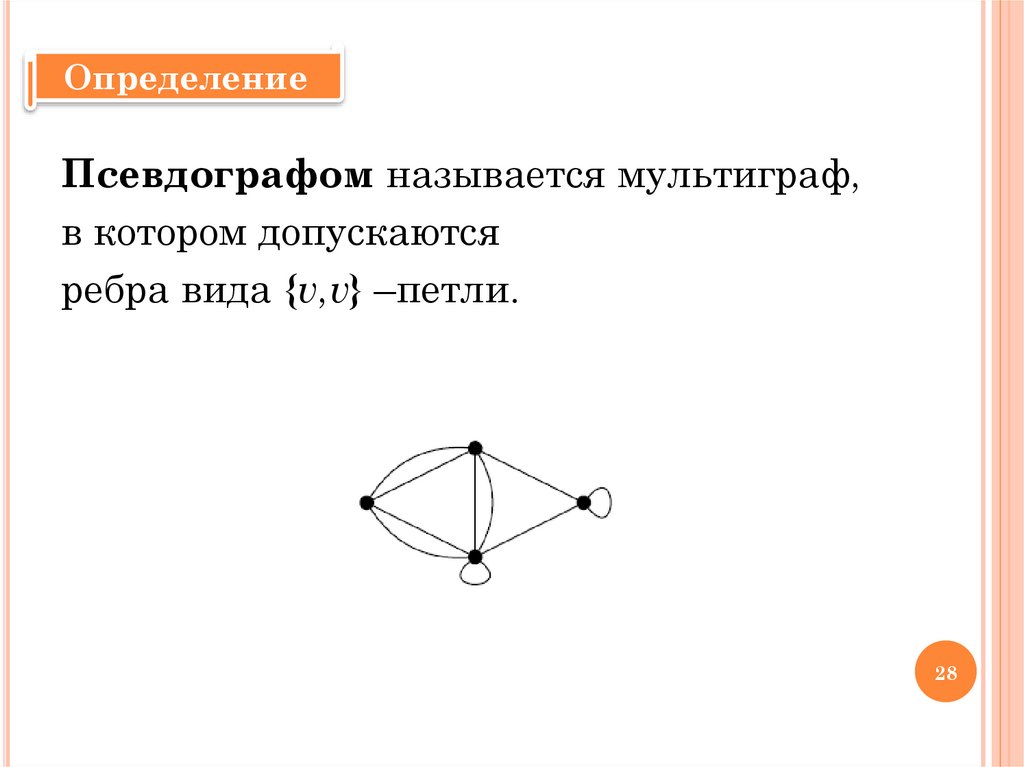
ОпределениеПсевдографом называется мультиграф,
в котором допускаются
ребра вида {v,v} –петли.
28
29.
ПОДГРАФЫОпределение
Граф H называется подграфом графа G,
если VH VG, EH EG
// H содержится в G
29
30.
ОпределениеПодграф H называется остовным G,
если VH VG .
30
31.
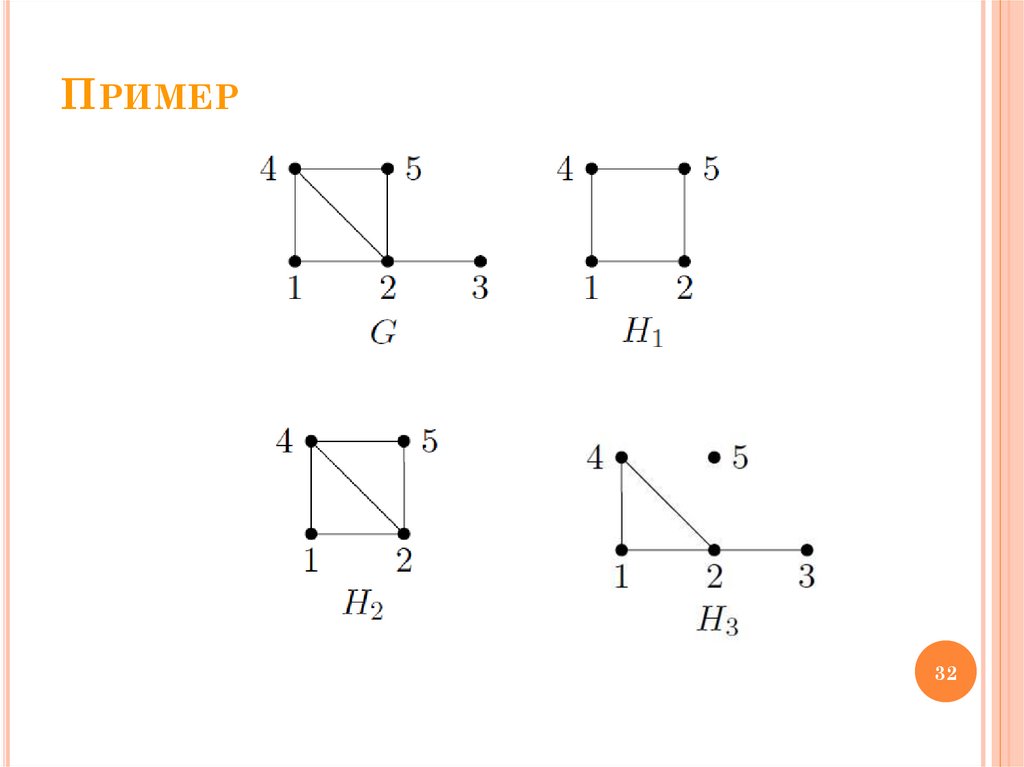
ОпределениеПодграф H называется порожденным
или индуцированным множеством U,
если VH U , EH {{u, v} u, v U }.
31
32.
ПРИМЕР32
33.
СВЯЗНЫЕ ГРАФЫОпределение
Маршрутом, соединяющим вершины vi и vj,
называется последовательность
vi, ei,vi+1,ei+1, …, vj-1,ej-1,vj
вершин и ребер (иногда только вершин), в
которой ek=vk+vk+1,
k i, j 1.
Число ребер в маршруте называется его
длиной.
33
34.
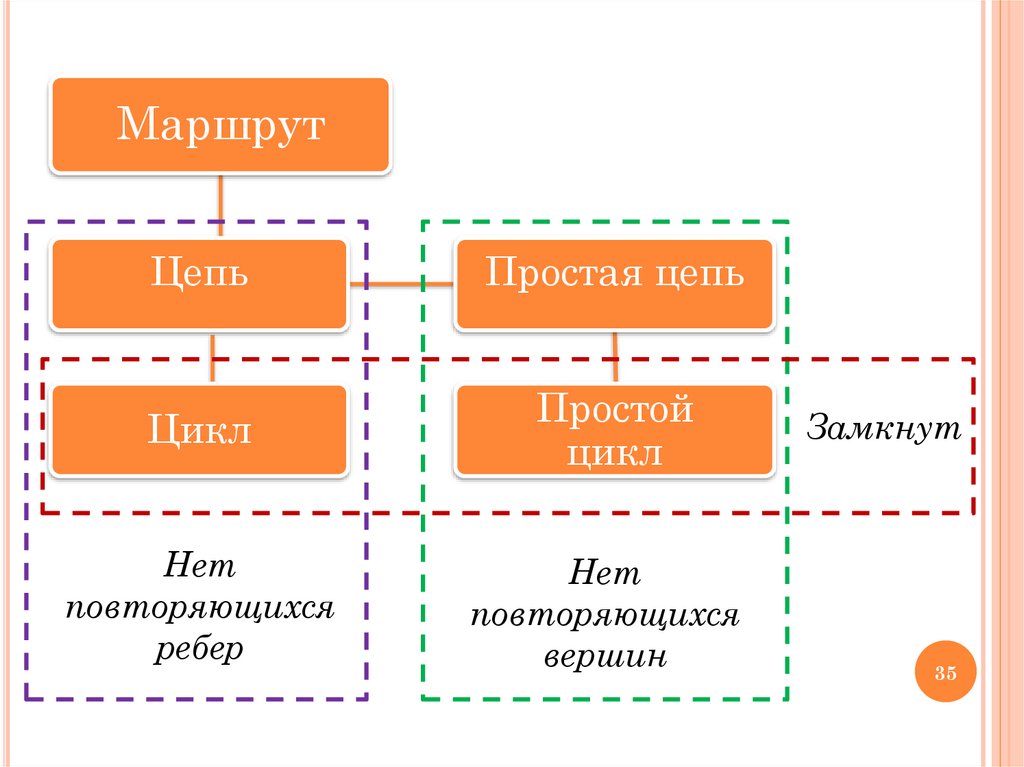
ОпределениеМаршрут называется цепью,
если в нем нет повторяющихся ребер.
Маршрут называется простой цепью,
если в нем нет повторяющихся вершин и он
является цепью.
Маршрут называется циклом,
если он замкнут и является цепью.
Маршрут называется простым циклом,
если он замкнут и является простой цепью.
34
35.
МаршрутЦепь
Цепь
Простая цепь
Цикл
Простой
цикл
Нет
повторяющихся
ребер
Нет
повторяющихся
вершин
Замкнут
35
36.
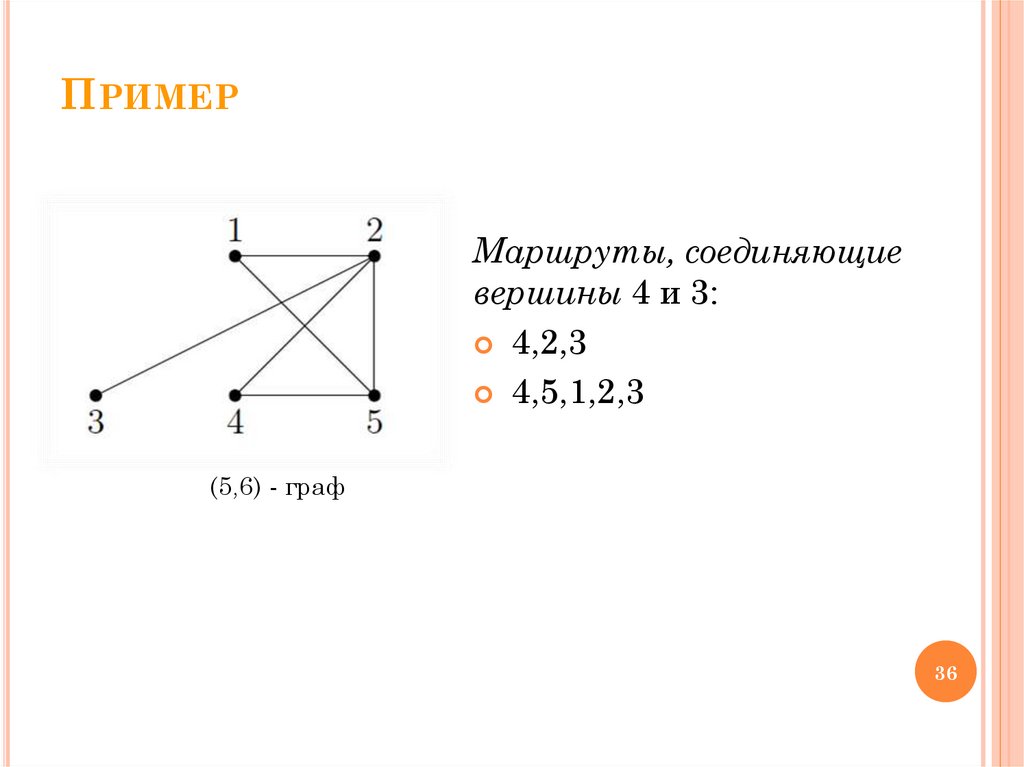
ПРИМЕРМаршруты, соединяющие
вершины 4 и 3:
4,2,3
4,5,1,2,3
(5,6) - граф
36
37.
ОпределениеГраф называется связным, если любые две
его несовпадающие вершины соединены
маршрутом.
Всякий максимальный связный подграф
графа называется связной компонентой
графа.
37
38.
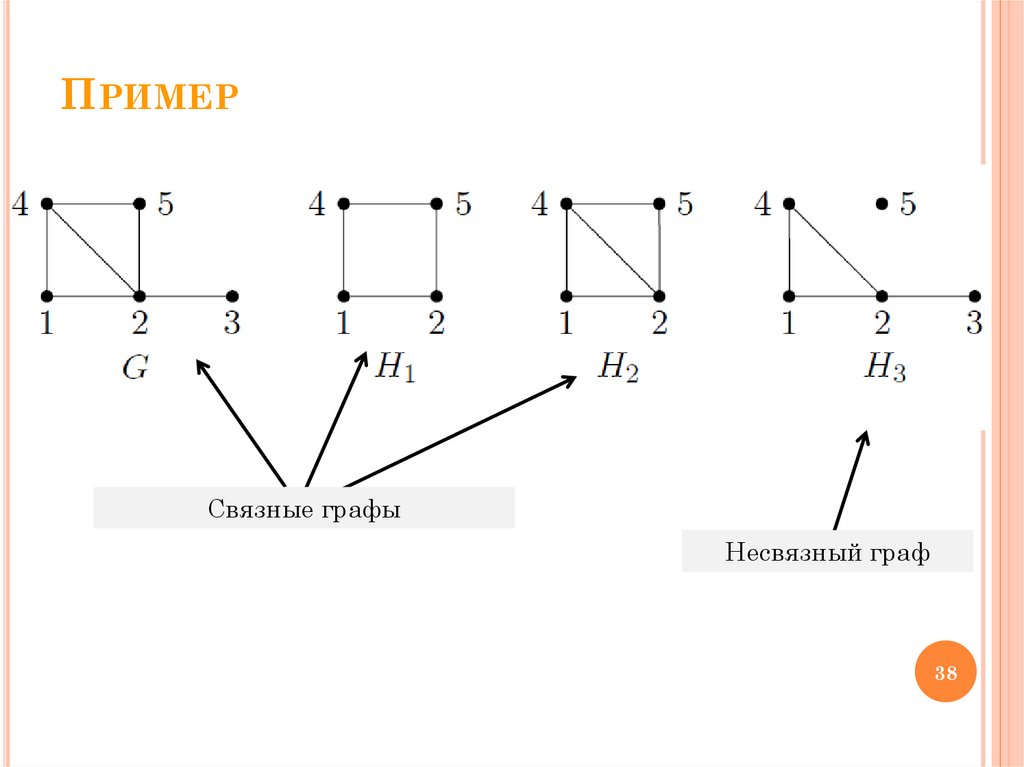
ПРИМЕРСвязные графы
Несвязный граф
38
39.
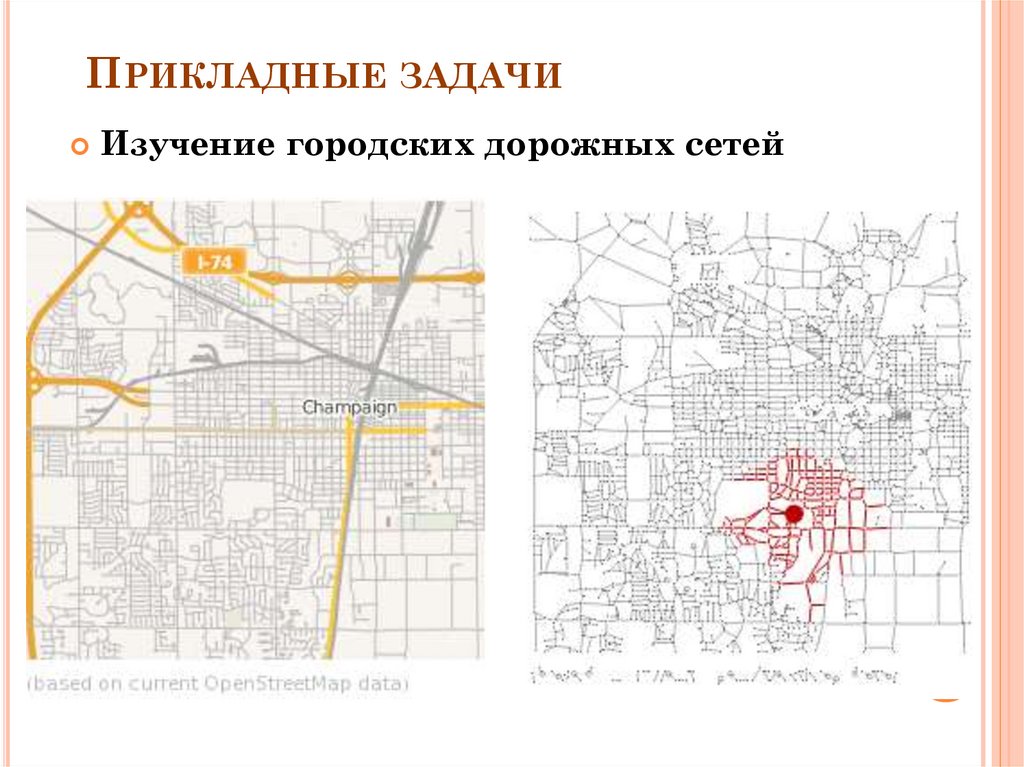
ПРИКЛАДНЫЕ ЗАДАЧИИзучение городских дорожных сетей
39
40.
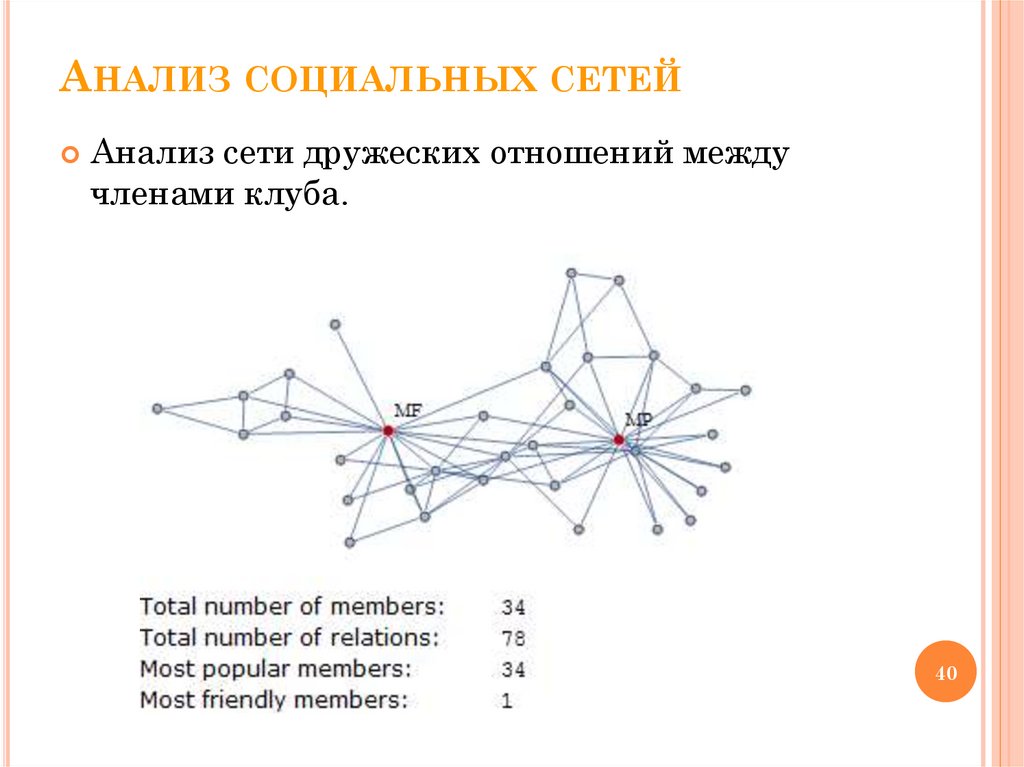
АНАЛИЗ СОЦИАЛЬНЫХ СЕТЕЙАнализ сети дружеских отношений между
членами клуба.
40
41.
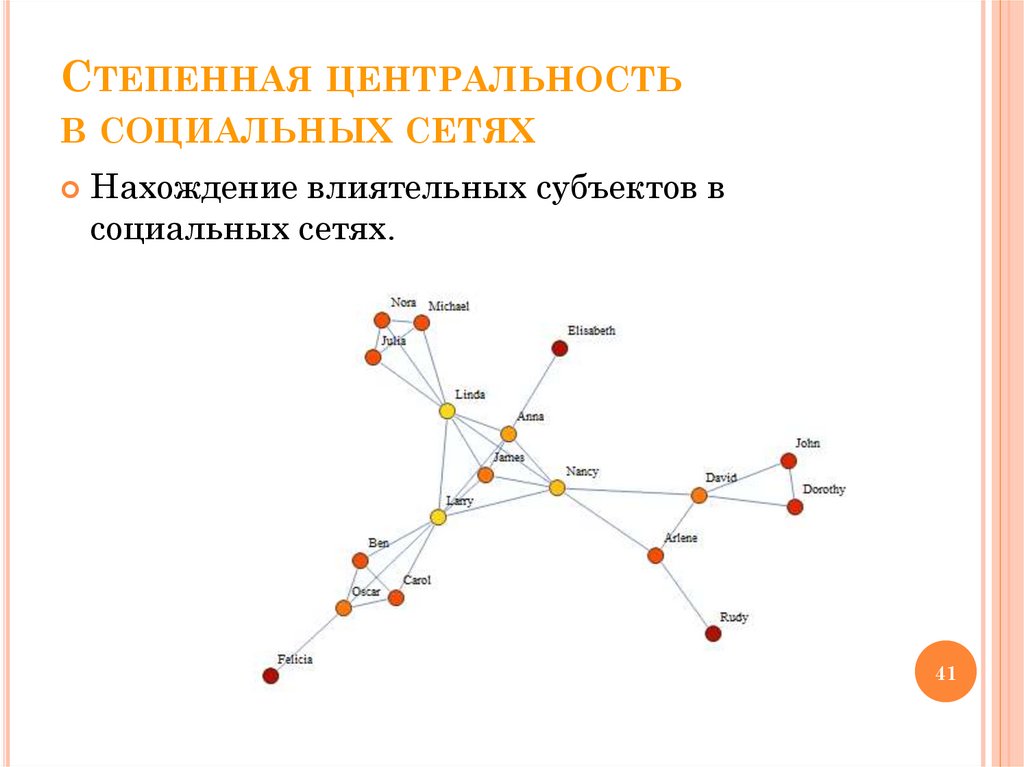
СТЕПЕННАЯ ЦЕНТРАЛЬНОСТЬВ СОЦИАЛЬНЫХ СЕТЯХ
Нахождение влиятельных субъектов в
социальных сетях.
41
42.
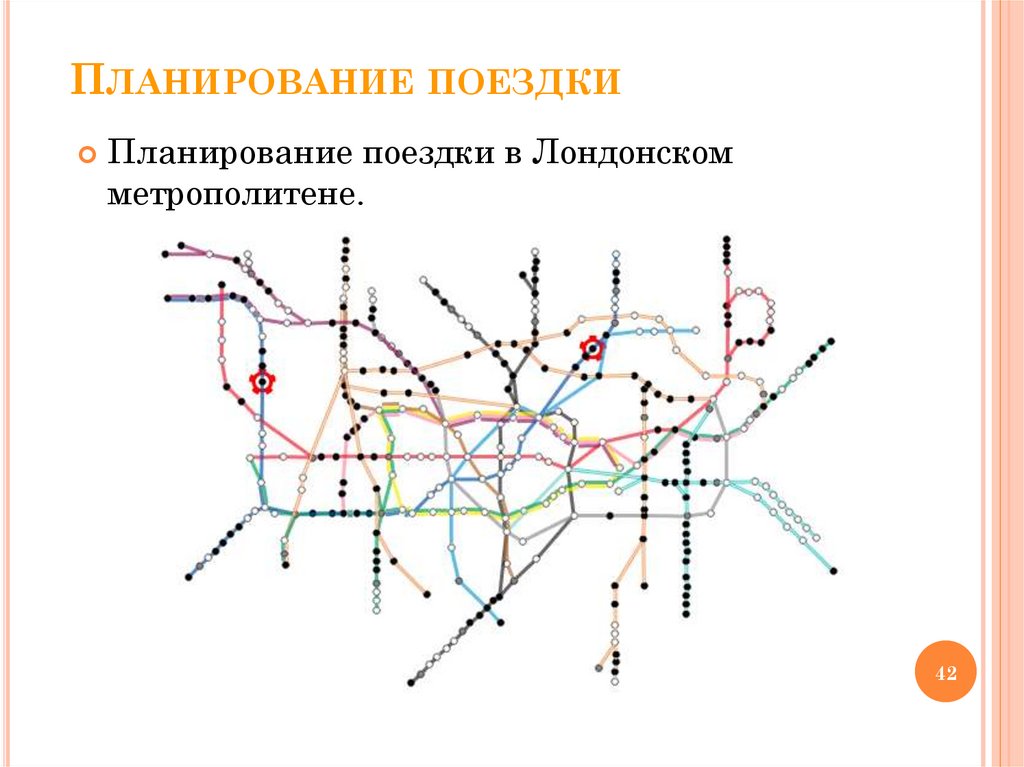
ПЛАНИРОВАНИЕ ПОЕЗДКИПланирование поездки в Лондонском
метрополитене.
42
43.
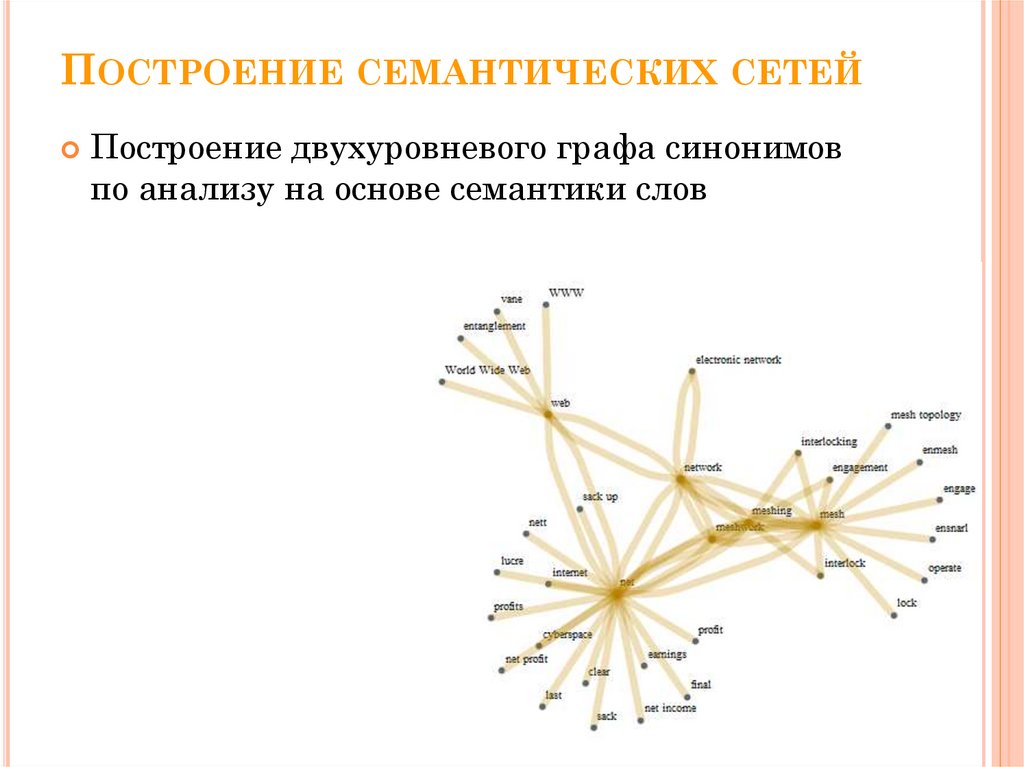
ПОСТРОЕНИЕ СЕМАНТИЧЕСКИХ СЕТЕЙПостроение двухуровневого графа синонимов
по анализу на основе семантики слов
43
44.
СТРУКТУРА ВСЕМИРНОЙ ПАУТИНЫСеть страниц корпоративного сайта.
44
45.
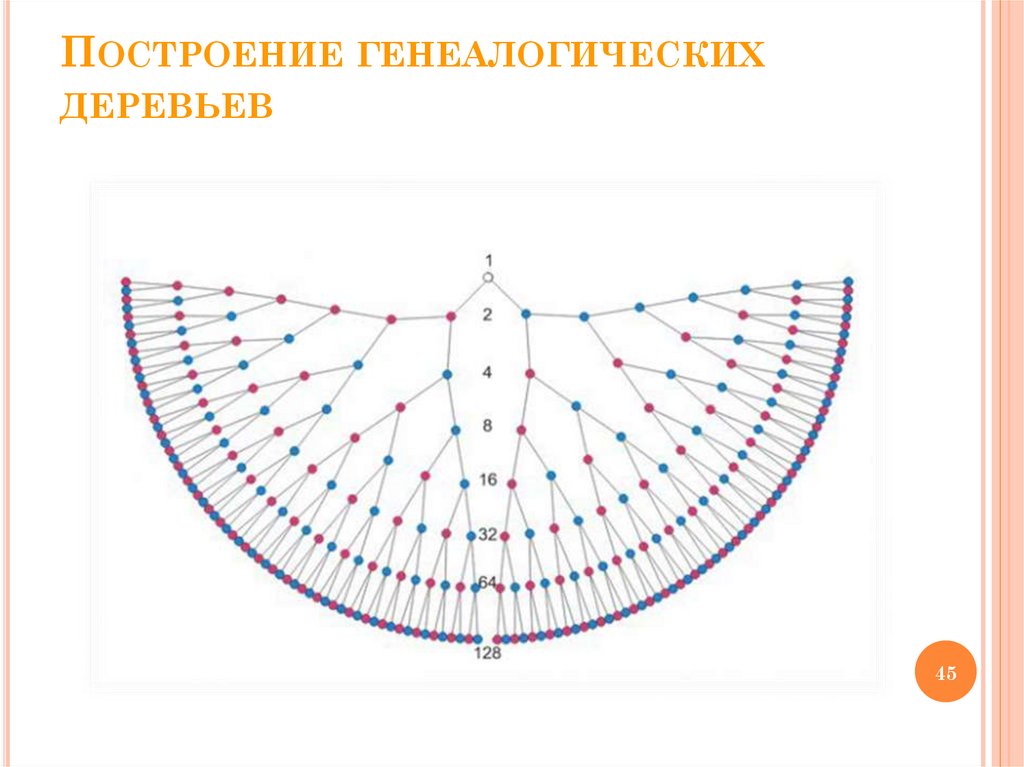
ПОСТРОЕНИЕ ГЕНЕАЛОГИЧЕСКИХДЕРЕВЬЕВ
45
46.
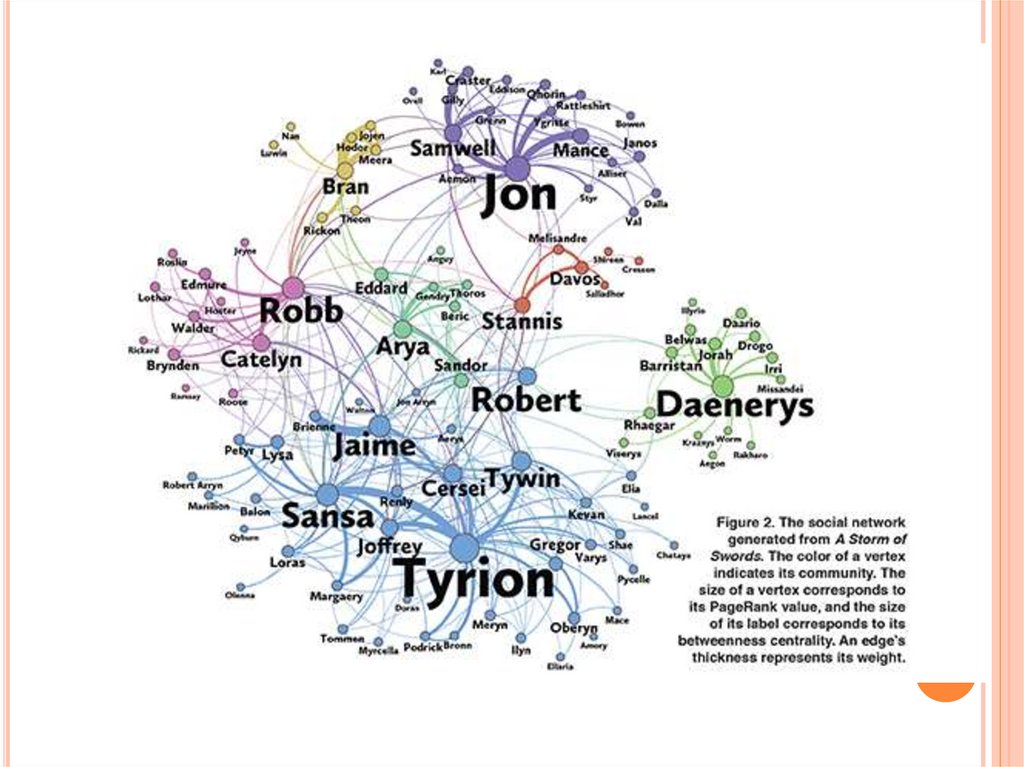
МАТЕМАТИКИ ВЫЧИСЛИЛИ ГЛАВНОГОПЕРСОНАЖА «ИГРЫ ПРЕСТОЛОВ»
Профессор математики Эндрю Беверидж из колледжа
Макалестер и его студентка Джи Шан с помощью теории
графов «вычислили» главных персонажей серии книг
«Игра престолов».
Их работа опубликована в журнале Math Horizons
4.04.2016.
46
47.
4748.
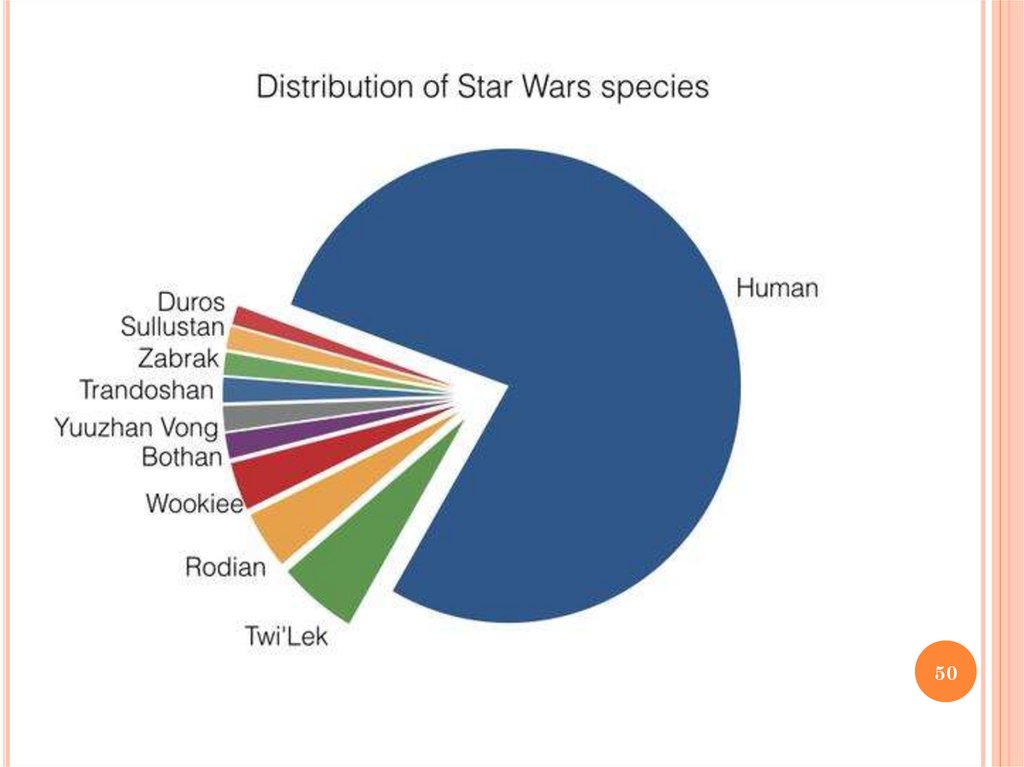
ИЗУЧЕНИЕ ВСЕЛЕННОЙ«ЗВЕЗДНЫХ ВОЙН»
48

























 mathematics
mathematics








