Similar presentations:
Математическая логика и теория алгоритмов
1. Математическая логика и теория алгоритмов
Доцент каф. АОИ, к.т.н. Перемитина Татьяна ОлеговнаМатематическая логика
и теория алгоритмов
Логика предикатов
2. Логика предикатов
Основные понятия логики предикатов.Логические операции над предикатами.
Кванторные операции. Формулы логики
предикатов.
Равносильные формулы логики
предикатов.
Нормальная форма записи формул
логики предикатов.
2
3.
ЗадачаПроверьте правильность
рассуждения:
логического
«Все люди смертны. Сократ человек.
Следовательно, Сократ смертен».
3
4.
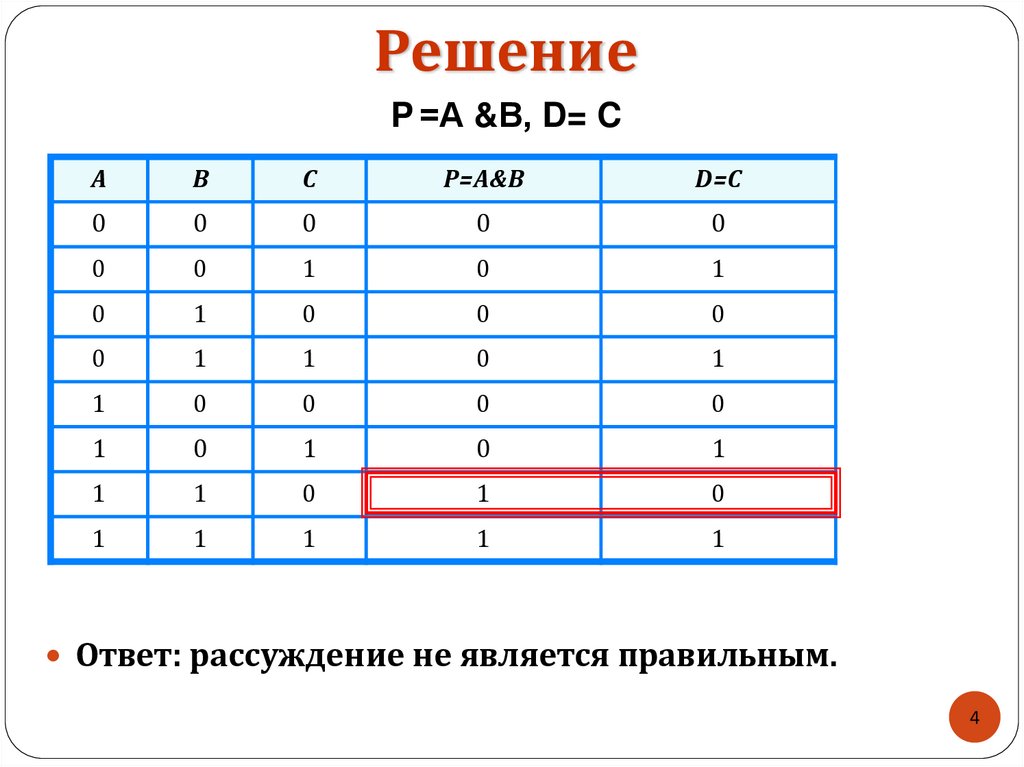
РешениеP =А &В, D= C
A
B
C
P=А&В
D=C
0
0
0
0
0
0
0
1
0
1
0
1
0
0
0
0
1
1
0
1
1
0
0
0
0
1
0
1
0
1
1
1
0
1
0
1
1
1
1
1
Ответ: рассуждение не является правильным.
4
5. Структура суждений
S есть PСубъект (S) – это то, о чем (ком) идет
речь в суждении.
Предикат (Р) – это то, что говорится о
субъекте.
Квантор – это указатель на объем
субъекта (все или некоторые).
5
6. Пример 1
«Все металлы электропроводны»Квантор – «Все»;
Субъект – «металлы»;
Предикат – «электропроводны»;
Связка – «есть».
6
7. Задача 1
«Некоторые студенты являютсяспортсменами»
Сопоставьте:
1. Связка
A. Студенты
2. Субъект
B. Спортсмены
3. Предикат
C. Некоторые
4. Квантор
D. Являются (есть)
7
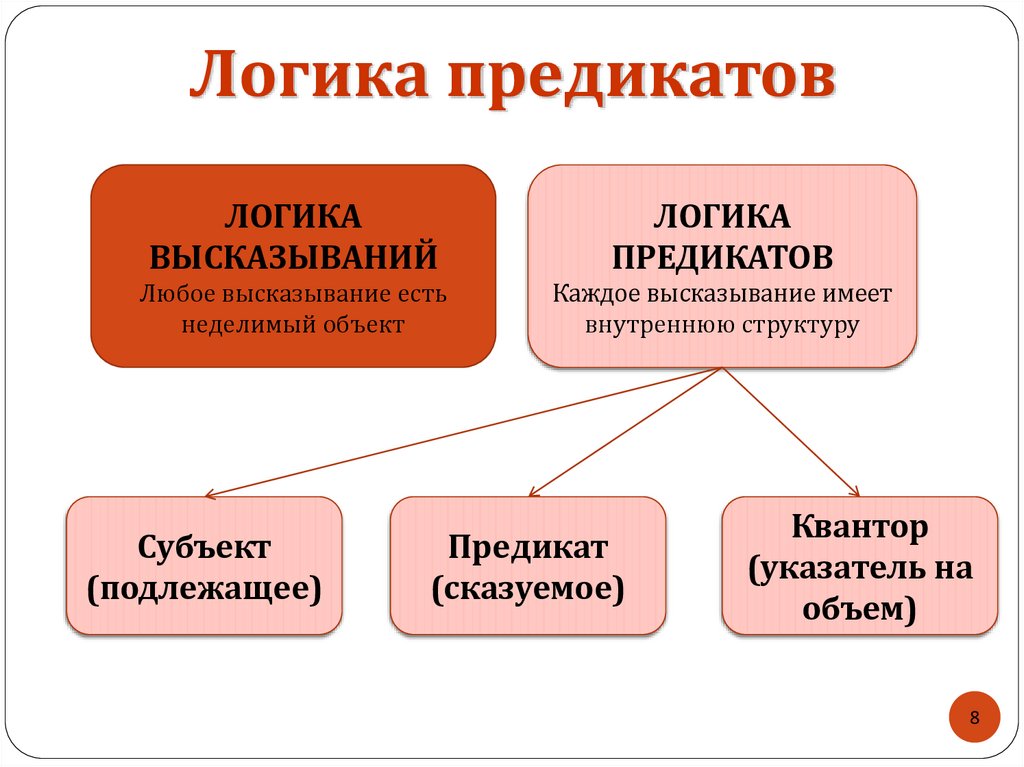
8. Логика предикатов
ЛОГИКАВЫСКАЗЫВАНИЙ
ЛОГИКА
ПРЕДИКАТОВ
Любое высказывание есть
неделимый объект
Каждое высказывание имеет
внутреннюю структуру
Субъект
(подлежащее)
Предикат
(сказуемое)
Квантор
(указатель на
объем)
8
9. Одноместные предикаты
Р( х) " х является смертным"Q( х) " х является человеком"
х 0
R ( x) " х является положительным
числом"
9
10.
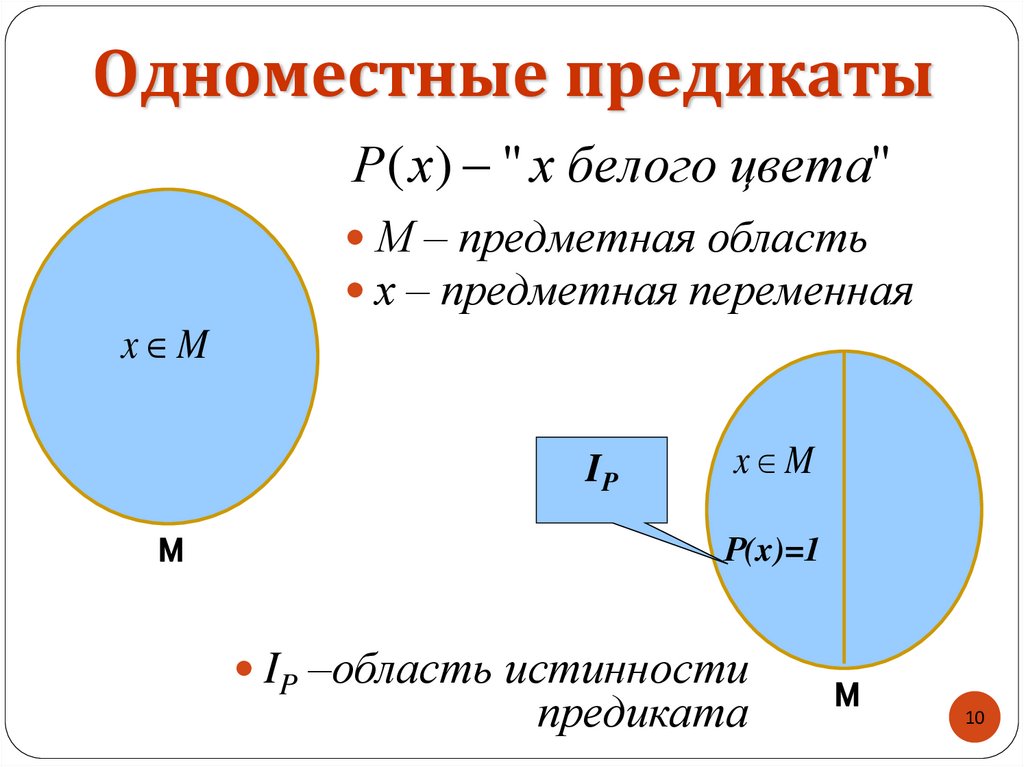
Одноместные предикатыР( х) " х белого цвета"
М – предметная область
х – предметная переменная
x M
IP
M
x M
Р(x)=1
IP –область истинности
предиката
M
10
11.
Пример 2R( x) : M {0,1}
х 0
R ( x) " х является положительным
числом"
M {1, 2, 3, 4, 5, 1}
I P {1, 2, 4, 5}
11
12.
Задача 2Q( x) " х является простым числом"
M {2, 3, 4, 5, 6, 7, 8, 9}
A. I P {3, 5, 7, 9}
B. I P {2, 3, 5, 7}
C. I P {2, 3, 5, 7, 9}
D. I P {2, 3, 4, 7, 9}
12
13.
Задача 3Q( x) " х 3х 2 0"
2
M R
I Q { 2, 1}
A.
I Q { 1, 2}
C.
B.
I Q {2, 1}
D. I Q {2, 1}
13
14.
РешениеQ( x) " х 3х 2 0"
2
D b 4ac 9 8 1
2
b D 3 1
х1
1;
2a
2
b D 3 1
х2
2.
2a
2
Правильный ответ А
14
15. Многоместный предикат
P( x1 ,..., xn )P( x1 , x2 , , xn ) : M {0,1}
n
M M 1 M 2 ..... M n
n
15
16. Многоместные предикаты
Р( х, у ) " х является учителем у"Q( х, y, z ) " х у z 0"
2
R( x, y, z , h) " х является отцом у,
дедом z , внуком h"
16
17.
Пример 3R( x, y) " х y 0"
2
2
M х {1, 2, 3}; M у { 2, 3, 4}
Q ( x, y ) " х y"
M х {1, 2, 3}; M у { 2, 3, 4}
17
18. Логические операции
UIP
IP
U
P (x )
P( x) & Q( x)
IP
IQ
I P IQ
P( x) Q( x)
U
IP
IQ
I P IQ
18
19.
Пример 4Р( x) " х кратно 2"
Q( x) " х является простым числом"
M {2, 3, 4, 5, 6, 7, 8, 9}
I P { 2, 4, 6, 8}; I Q { 2, 3, 5, 7}
Определим:
I P &Q ;
I P Q ;
I P ; IQ .
19
20.
Пример 4I P { 2, 4, 6, 8}; I Q { 2, 3, 5, 7}
I P &Q { 2};
I P Q { 2,3,4,5,6,7,8};
I P { 3,5,7,9};
I Q {4,6,8,9}.
20
21.
Задача 4I P { 3,5,7,9}; I Q {4,6,8,9}.
A.
I P&Q {6, 9}
C.
I P&Q {9}
B.
I P&Q {3, 6}
D.
I P&Q {3}
21
22.
Задача 5P( x) " х 3x 2 0"
2
Q( x) " х 4 x 3 0"
2
A.
I P &Q { 2}
B.
I P &Q { 1}
C.
I P &Q { 1, 2}
M R
22
23. Квантор всеобщности
Все S (не) есть PP (x ) , x – свободная переменная
xP(x) , x – связанная квантором
всеобщности переменная
n
& P( xi ) P( x1 ) & P( x2 ) & ... & P( xn ) 1.
i 1
23
24. Квантор существования
Некоторые S (не) есть PP (x ) , x – свободная переменная
xP(x) , x – связанная квантором
существования переменная
n
P( xi ) P( x1 ) P( x2 ) ... P( xn ) 1.
i 1
24
25.
Пример 5Р( x) " х является нечетным числом"
M {2, 3, 5, 7}
xP( x) 1;
хР( х) 0.
25
26.
Пример 6Q( x) " х является простым числом"
M {2, 3, 5, 7}
xQ( x) 1;
хQ( х) 1.
26
27. Основные равносильности логики предикатов
2728. Предваренная нормальная форма
1. Перейти от операций и ↔ ксимволам &, , .
2. Внести все отрицания внутрь
формулы.
3. Вынести все кванторы в начало
формулы.
28
29.
Пример 7Пусть дана формула:
F ( x( P( x) yQ( y)))
Необходимо записать ее в ПНФ
F ( x( P( x) yQ( y )))
x( ( P( x) yQ( y )))
x( P ( x) & ( yQ ( y )))
x( P ( x) & ( y Q( y )))
x y( P( x) & Q( y)).
29



























 mathematics
mathematics








