Similar presentations:
Математическая логика и теория алгоритмов
1. Математическая логика и теория алгоритмов
Доцент каф. АОИ, к.т.н.Перемитина Татьяна Олеговна
Математическая логика
и теория алгоритмов
Нормальные формы формул
алгебры высказываний
2. Нормальные формы формул алгебры высказываний
равносильные преобразования формулалгебры высказываний;
критерий равносильности;
ДНФ (КНФ) и СДНФ (СКНФ);
проверка правильности логических
рассуждений.
2
3. Равносильные преобразования
Равносильные преобразованиялогических формул имеют то же
назначение, что и преобразования формул
в обычной алгебре.
Они служат для упрощения формул или
приведения их к определённому виду
путем использования основных законов
алгебры логики.
3
4. Пример 1
Пусть даны две формулы: Две формулы алгебры высказыванийF 1 А B,
называются равносильными, если они
F 2 А B
значения на одних и тех же наборах
принимают одинаковые истинностные
своих переменных.
Проверим их на равносильность (по определению):
А
В
˥А
˥А→В
А
В
АV В
0
0
1
0
0
0
0
0
1
1
1
0
1
1
1
0
0
1
1
0
1
1
1
0
1
1
1
1
4
5.
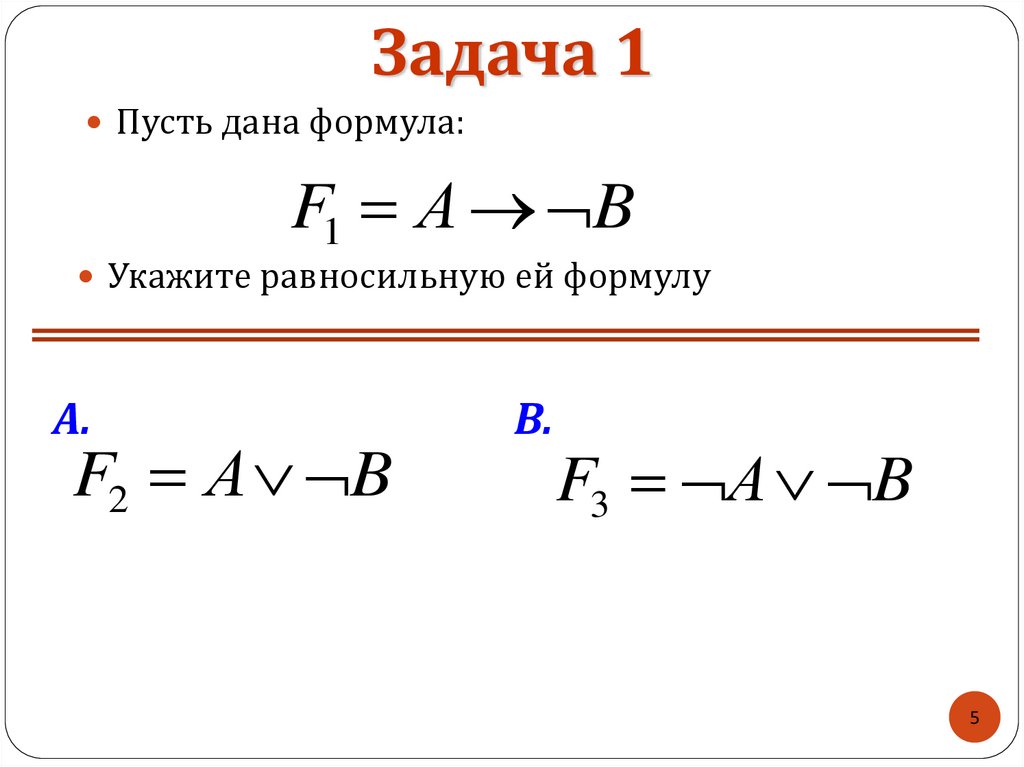
Задача 1Пусть дана формула:
F1 А B
Укажите равносильную ей формулу
А.
F2 А B
В.
F3 А B
5
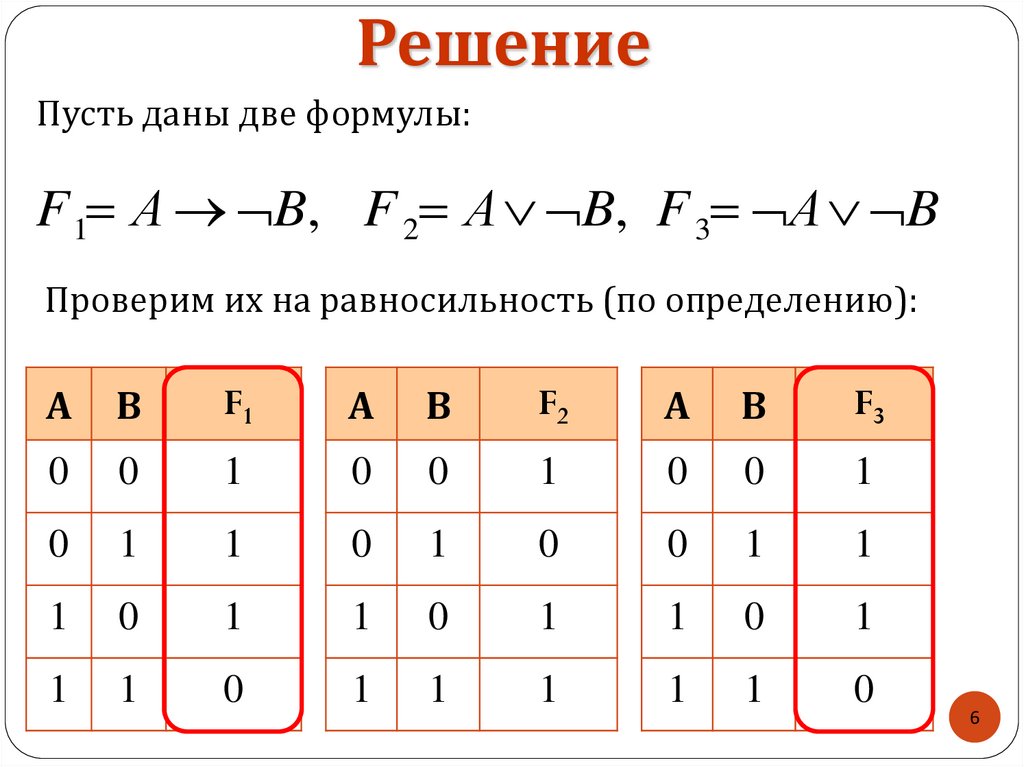
6. Решение
Пусть даны две формулы:F 1 А B, F 2 А B, F 3 А B
Проверим их на равносильность (по определению):
А
В
F1
А
В
F2
А
В
F3
0
0
1
0
0
1
0
0
1
0
1
1
0
1
0
0
1
1
1
0
1
1
0
1
1
0
1
1
1
0
1
1
1
1
1
0
6
7.
Проверка равносильностиF1 =A v (А & В), F2 = A
Определение:
Две формулы алгебры высказываний называются равносильными, если они
принимают одинаковые истинностные значения на одних и тех же наборах
своих переменных.
A
B
А&В
F1
F2
0
0
0
0
0
0
1
0
0
1
1
0
0
1
1
1
1
1
Невозможно проверить равносильность формул с
разным числом переменных «по определению».
7
8. Признак равносильности формул
Формула F1 равносильна формуле F2 тогда и толькотогда, когда эквиваленция F1↔F2 является
тождественно истинной формулой.
F1
F2 ( F1 F2 ) 1.
8
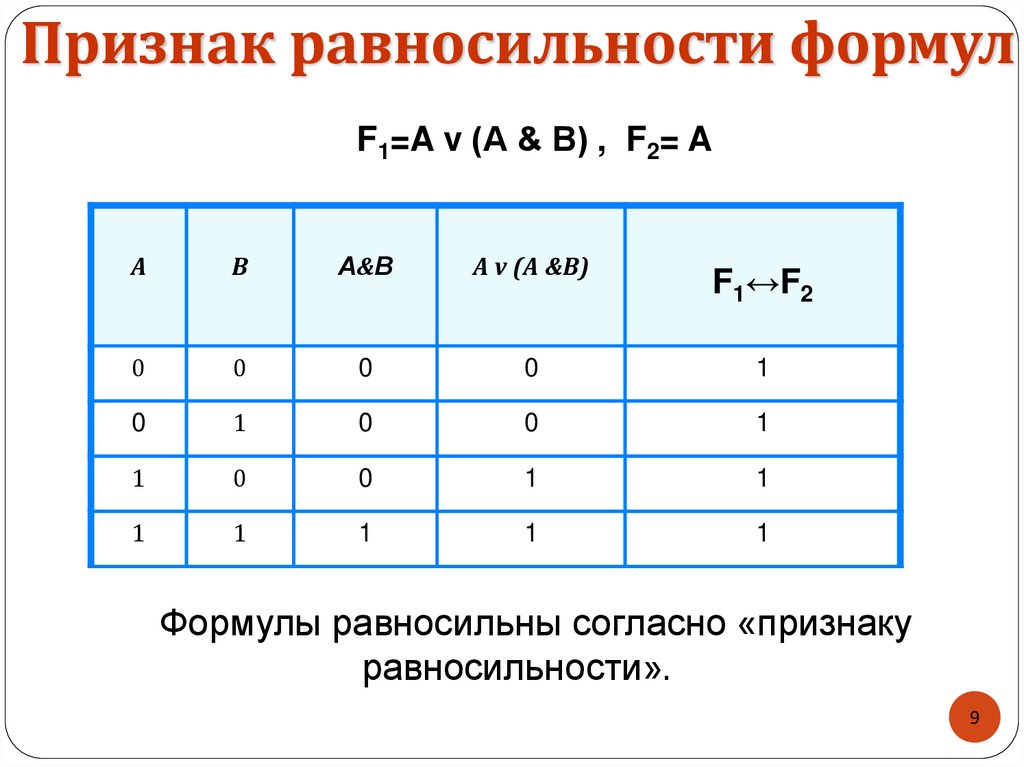
9.
Признак равносильности формулF1=A v (А & В) , F2= A
A
B
А&В
A v (А &В)
F1↔F2
0
0
0
0
1
0
1
0
0
1
1
0
0
1
1
1
1
1
1
1
Формулы равносильны согласно «признаку
равносильности».
9
10. Основные равносильности логики высказываний
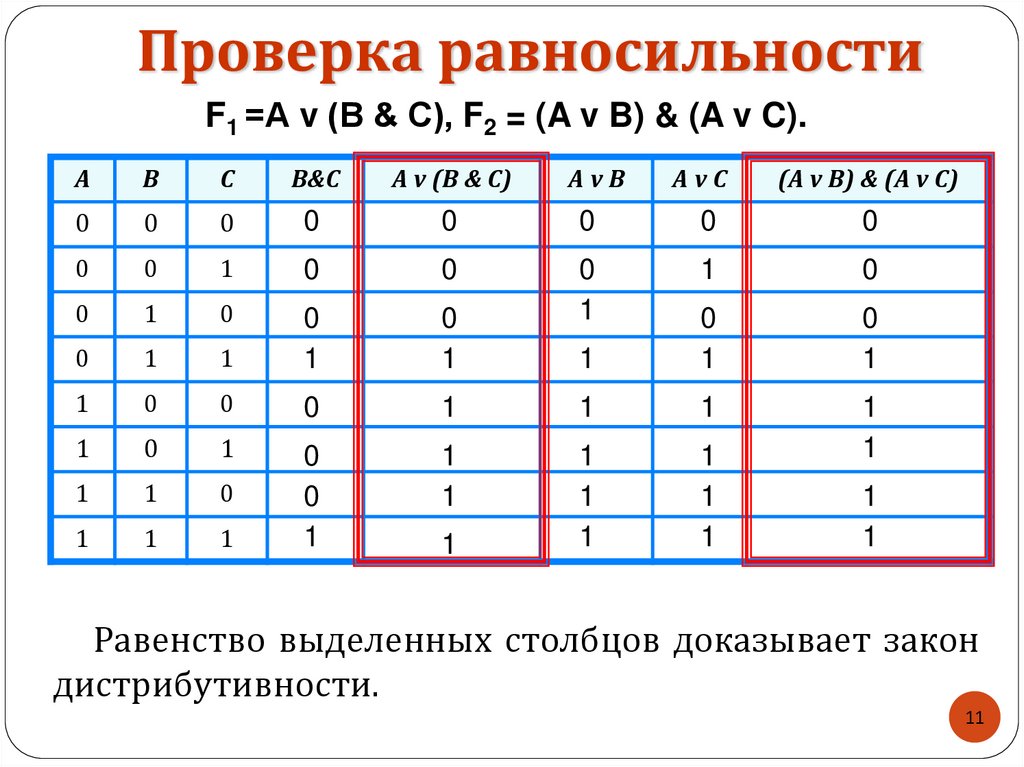
1011.
Проверка равносильностиF1 =А v (В & C), F2 = (A v B) & (A v C).
A
B
C
B&C
A v (B & C)
AvB
AvC
(A v B) & (A v C)
0
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
1
0
1
1
0
0
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
Равенство выделенных столбцов доказывает закон
дистрибутивности.
11
12.
Задача 2Пусть дана формула:
( А B) С
Укажите равносильную ей формулу
A. А B С
B. ( А & B ) С
C. ( А & B ) С
D. А & B & С
12
13. Решение
( А B) С ( А & B) CПравильный ответ В
13
14.
Задача 3Пусть дана формула:
( А B) С
Укажите равносильную ей формулу
A. А & B С
B. ( А & B ) С
А B С
D. А & B & С
C.
14
15. Решение
( А B) С( А & В ) С
Правильный ответ В
15
16.
Подформулы формулПусть дана формула:
( А & B) ( A & B) & ( A B)
Выпишем все подформулы данной формулы:
А, B, A, B, ( А & B), ( A & B),
( A B), ( A & B) & ( A B)
Элементарные конъюнкции (ЭК):
( А & B) и ( A & B)
Элементарная дизъюнкция(ЭД): ( A B )
16
17.
Нормальные формы формулалгебры высказываний
•Конъюнктивная
нормальная форма (КНФ):
( X1 X 2 ) & ( X 3 X 2 X1)
•Дизъюнктивная
нормальная форма (ДНФ):
( X1 & X 2 ) ( X 3 & X 2 & X1)
17
18.
Нормальные формы формулалгебры высказываний
Любую формулу логики высказываний можно привести
равносильными преобразованиями к ДНФ(КНФ).
Шаг 1. Преобразовать формулу, чтобы присутствовали
только операции:
отрицание;
конъюнкция;
дизъюнкция.
Воспользоваться законами:
Замена импликации № 11;
Замена эквиваленции № 12.
18
19.
Нормальные формы формулалгебры высказываний
Шаг 2. Преобразовать формулу к такому виду, чтобы
знак отрицания стоял только перед переменными.
Воспользоваться законом де Моргана № 8.
Шаг 3. Преобразовать формулу, пользуясь первым
дистрибутивным законом (№5).
При необходимости использовать законы
идемпотентности (№7), коммутативности (№3),
ассоциативности (№4).
19
20.
ПримерПусть дана формула:
( A B) ( B & C )
Преобразуем формулу к ДНФ:
Шаг 1 : ( А B) ( В & C )
Шаг 2 : ( А & B) ( В & C )
20
21.
Задача 4Укажите КНФ формулы:
( A B) & ( B C )
A.
( A B ) & ( B C )
B.
( A & B) ( B & C )
C.
( A B) & ( B C )
21
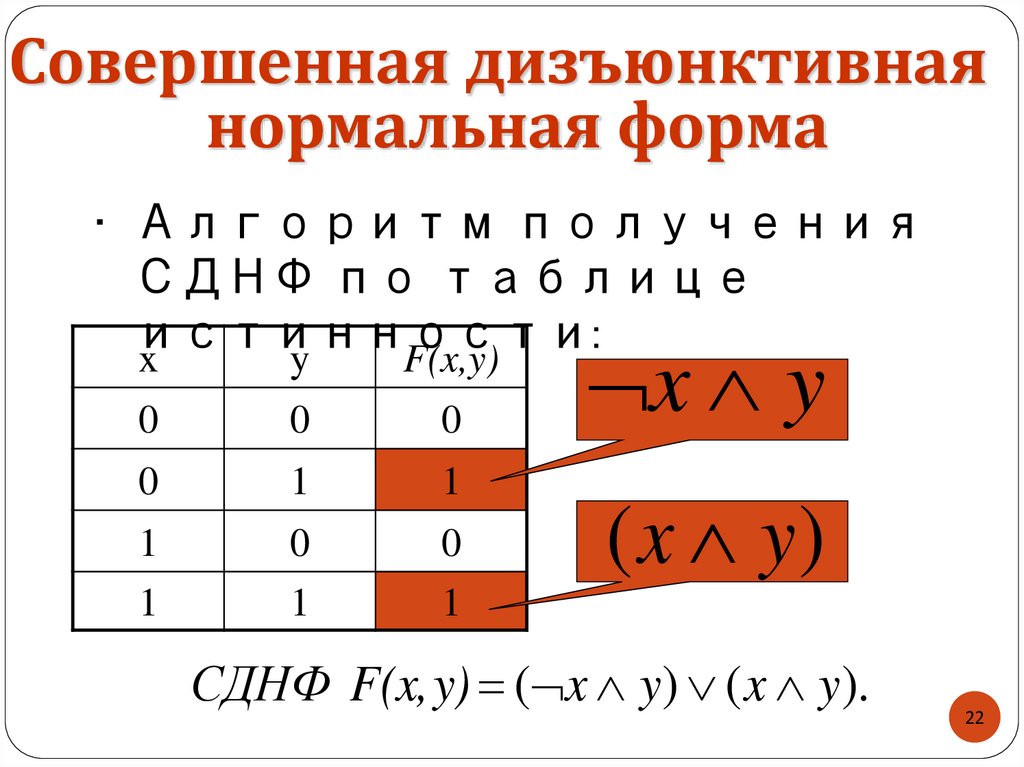
22.
Совершенная дизъюнктивнаянормальная форма
• Алгоритм получения
СДНФ по таблице
истинности:
x
y
F(x,y)
0
0
0
0
1
1
1
0
0
1
1
1
x y
( x y)
СДНФ F(x, y) ( x y) ( x y).
22
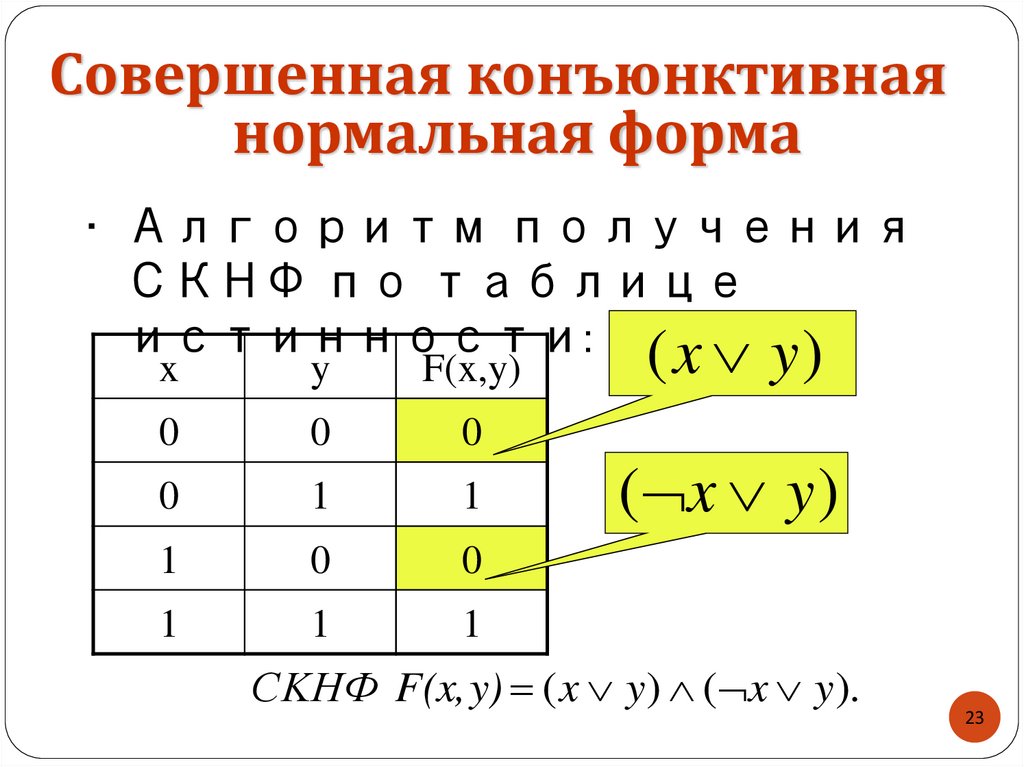
23.
Совершенная конъюнктивнаянормальная форма
• Алгоритм получения
СКНФ по таблице
истинности: ( x y )
x
y
F(x,y)
0
0
0
0
1
1
1
0
0
1
1
1
( x y )
СKНФ F(x, y) ( x y) ( x y).
23
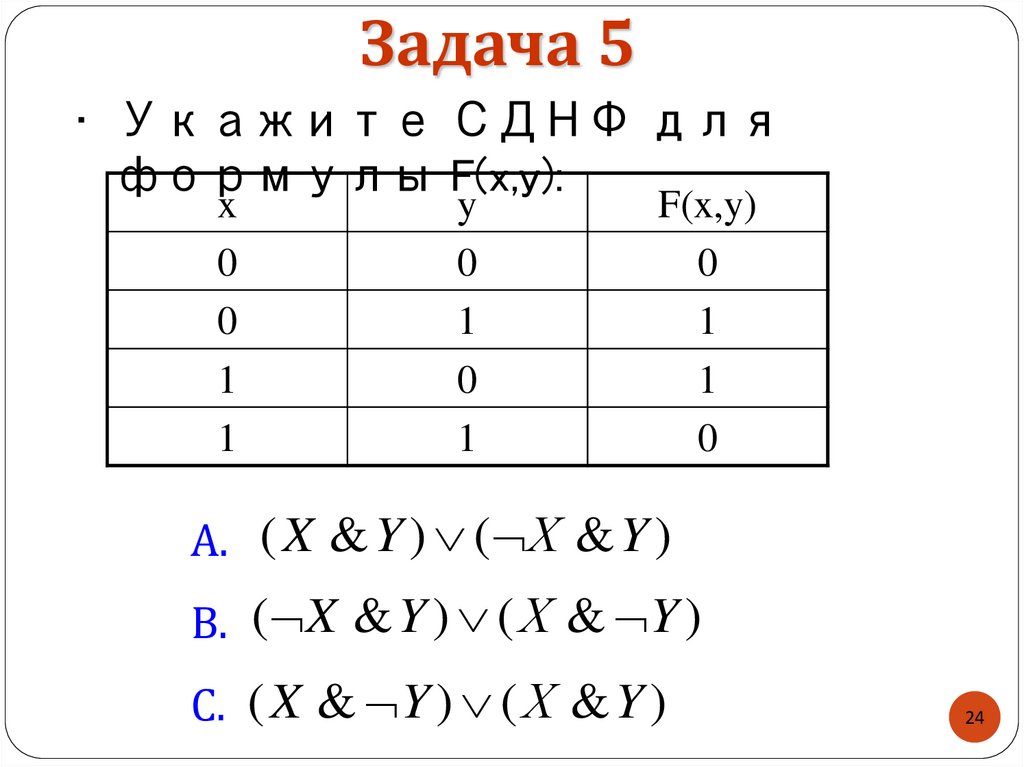
24.
Задача 5• Укажите СДНФ для
формулы F(x,y):
x
0
0
1
1
y
0
1
0
1
F(x,y)
0
1
1
0
A. ( X & Y ) ( Х & Y )
B. ( X & Y ) ( Х & Y )
C. ( X & Y ) ( Х & Y )
24
25. Логическое следование формул
Логически правильное рассуждение будемзаписывать в виде схемы рассуждения:
P1, P2,…,Pm
D
25
26.
ПримерПроверьте правильность
рассуждения:
логического
«Если в параллелограмме диагонали
ортогональны, то параллелограмм – ромб.
В
данном
случае
диагонали
не
ортогональны, следовательно, данный
параллелограмм – не ромб».
26
27.
РешениеИмеем следующие высказывания:
А ={в параллелограмме диагонали
ортогональны};
В = {параллелограмм – ромб};
P1 A B
P2 А
D В
27
28.
DB
P
A12
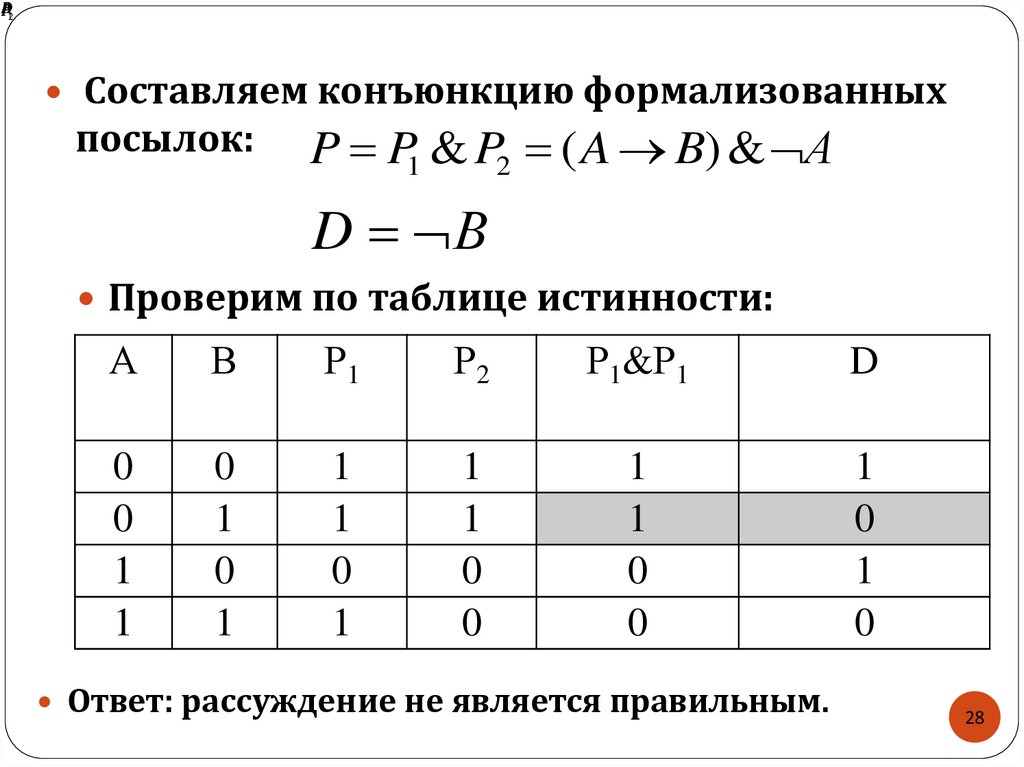
Составляем конъюнкцию формализованных
посылок:
P P1 & P2 ( A B) & А
D В
Проверим по таблице истинности:
А
В
Р1
Р2
Р1&Р1
D
0
0
1
1
0
1
0
1
1
1
0
1
1
1
0
0
1
1
0
0
1
0
1
0
Ответ: рассуждение не является правильным.
28
29.
Задача 6Проверьте правильность
рассуждения:
логического
«Все люди смертны. Сократ человек.
Следовательно, Сократ смертен».
29






















 mathematics
mathematics








