Similar presentations:
Моделирование экономических систем. Основные понятия и определения
1.
1. МОДЕЛИРОВАНИЕ ЭКОНОМИЧЕСКИХСИСТЕМ. ОСНОВНЫЕ ПОНЯТИЯ И
ОПРЕДЕЛЕНИЯ
1.1. Модели и моделирование. Классификация
моделей
1.2. Математические модели и методы их
расчета
2.
1.1. Модели и моделирование. Классификациямоделей
Моделью называется объект-заместитель,
который в определенных условиях может
заменять объект-оригинал, воспроизводя
интересующие нас свойства и характеристики
оригинала.
познавательные (когнитивные) ориентированы на
приближении модели к реальности
форма организации и представления знаний, средство
соединения новых знаний с имеющимися
прагматические - средство управления, организации
практических действий, способ представления образцово
правильных действий или их результата, т.е. являются
рабочим представлением целей (планы, кодексы законов,
рабочие чертежи)
3.
В теории моделей моделированиемназывается результат отображения
одной абстрактной математической
структуры на другую - тоже
абстрактную, либо как результат
интерпретации первой модели в
терминах и образах второй.
3/23
4.
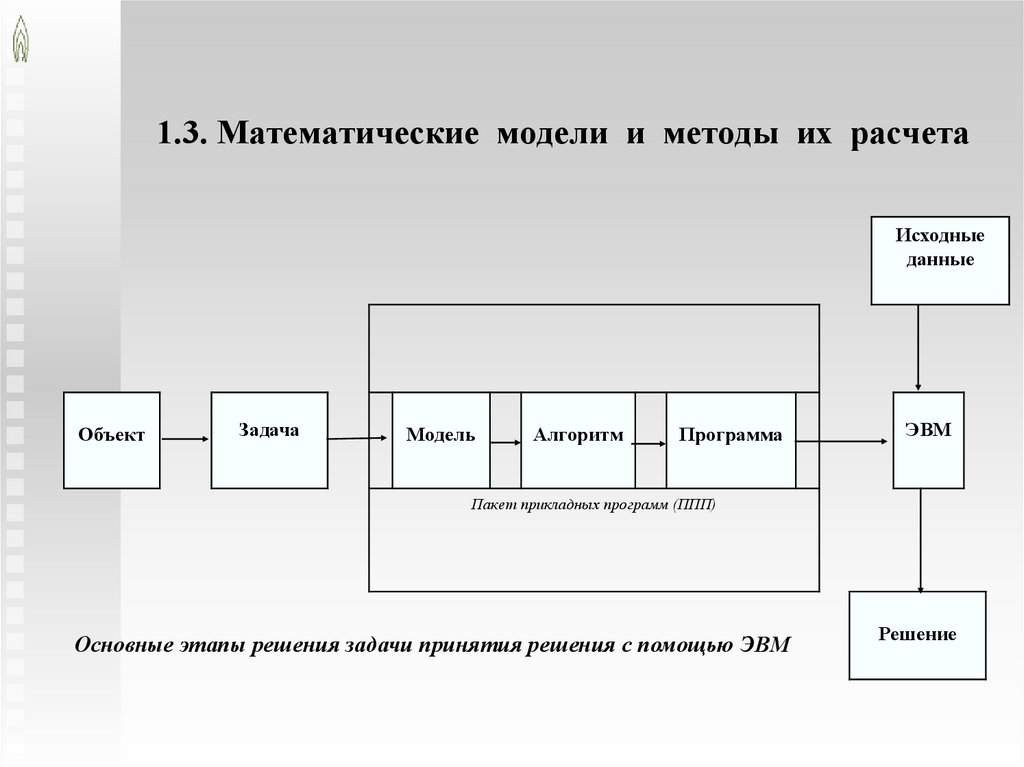
1.3. Математические модели и методы их расчетаИсходные
данные
Объект
Задача
Модель
Алгоритм
Программа
ЭВМ
Пакет прикладных программ (ППП)
Основные этапы решения задачи принятия решения с помощью ЭВМ
Решение
5.
математическая модель - это диагноззаболевания, алгоритм - это метод лечения.
Математическая модель - это система математических
соотношений, приближенно, в абстрактной форме
описывающих изучаемый процесс или систему.
Экономико-математическая модель - это математическая
модель, предназначенная для исследования экономической
проблемы.
Применение: планирование и оперативное управление
производством, управление трудовыми ресурсами, управление
запасами, распределение ресурсов, планировка и размещение
объектов, руководство проектом, распределение инвестиций и
т.п.
6.
Можно выделить следующие основные этапыпостроения математической модели:
Определение цели
2. Определение пapaметров модели, т.е. заранее известных
фиксированных факторов
3. Формирование управляющих переменных, изменяя значение
которых можно приближаться к поставленной цели.
Значения управляющих переменных являются решениями
задачи.
4. Определение области допустимых решений, т.е. тех
ограничений, которым должны удовлетворять управляющие
переменные.
5. Выявление неизвестных факторов, т.е. величин, которые
могут изменяться случайным или неопределенным образом.
6. Выражение цели через управляющие переменные,
параметры и неизвестные факторы, т.e. формирование
целевой функции, называемой также критерием
эффективности или критерием оптимальности задачи.
1.
7.
Решить задачу - это значит найти такоеоптимальное решение x X, чтобы при
фиксированных параметрах и с учетом
неизвестных факторов значения критерия
эффективности было по возможности
максимальным (минимальным).
Таким образом, оптимальное решение это решение, предпочтительное перед
другими по определенному критерию
эффективности (одному или нескольким).
8.
2. Применение линейногопрограммирования в
математических моделях
1.
2.
3.
Принцип оптимальности в планировании и
управлении
Задача линейного программирования
Поиск решения как средство решения задач
линейного и нелинейного моделирования
9.
ЛитератураЭкономико-математические методы и прикладные модели:
Учеб. пособие для вузов / Под ред. В.В. Федосеева. — 2-е
изд. М.: ЮНИТИ-ДАНА, 2005. — глава 2.
Вентцель Е.С. Исследование операций: Задачи, принципы,
методология. М.: Высшая школа, 2001.
Канторович Л.В. Экономический расчёт наилучшего
использования ресурсов. М.: Изд-во АН СССР, 1960.
Светлов Н.М., Светлова Г.Н. Построение и решение
оптимизационных моделей средствами программ MS Excel и
XA: Методические указания для студентов экономического
факультета / РГАУ – МСХА имени К.А. Тимирязева. М., 2005.
http://svetlov.timacad.ru/umk1/xa_1.doc
10.
2.1. Принцип оптимальности впланировании и управлении
Принцип оптимальности предполагает следующее:
наличие определённых ресурсов
наличие определённых технологических возможностей
цель хозяйственной деятельности
извлечение прибыли
удовлетворение потребностей
предотвращение угрозы
накопление знаний
и т.д.
Суть принципа:
планировать хозяйственную деятельность таким образом, чтобы
при имеющихся ресурсах и технологиях не существовало способа
достичь цели в большей степени, чем это предусматривает план
В полной мере этот принцип может быть реализован только с
помощью экономико-математических моделей
11.
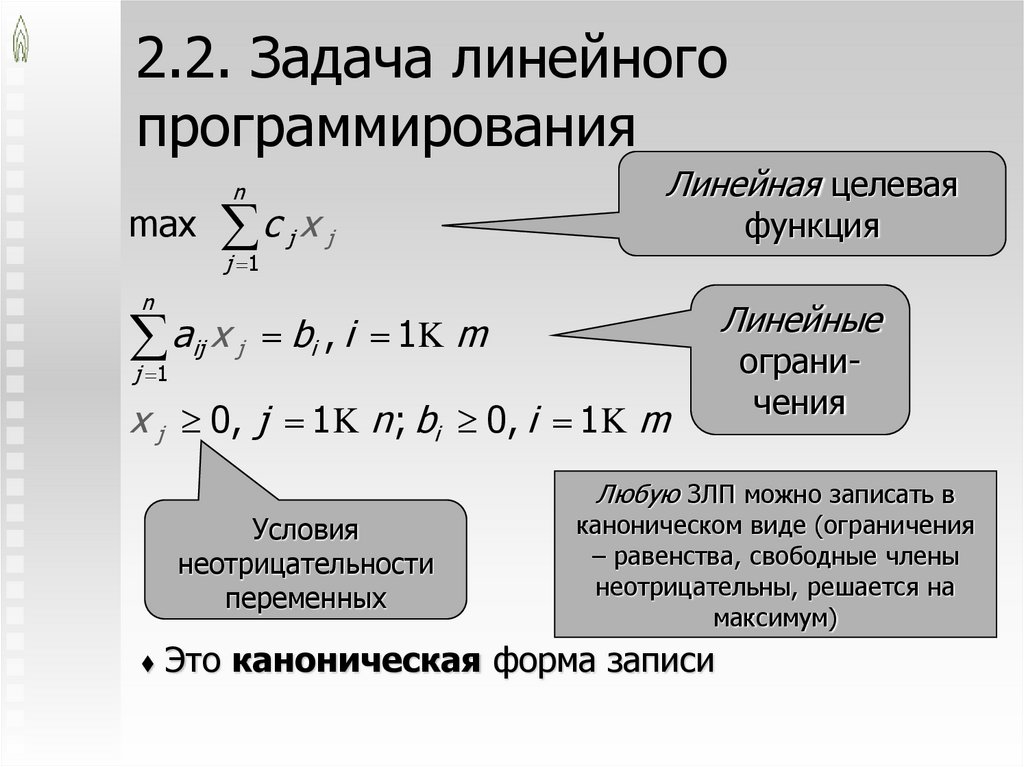
2.2. Задача линейногопрограммирования
max (min) c 1 x 1 c 2 x 2 K c n x n
a11x 1 a12 x 2 K a1n x n { , , } b1 ,
a 21x 1 a 22 x 2 K a 2n x n { , , } b2 ,
Линейная
целевая
функция
Линейные
ограничения
KKK
a m 1x 1 a m 2 x 2 K a mn x n { , , } bm ,
x j 0, j 1K n
Условия
неотрицательности
переменных
Это развёрнутая форма записи
12.
2.2. Задача линейногопрограммирования
n
max c j x j
Линейная целевая
функция
j 1
n
Линейные
aij x j bi , i 1K m
j 1
x j 0, j 1K n ; bi 0, i 1 K m
ограничения
Любую ЗЛП можно записать в
Условия
неотрицательности
переменных
каноническом виде (ограничения
– равенства, свободные члены
неотрицательны, решается на
максимум)
Это каноническая форма записи
13.
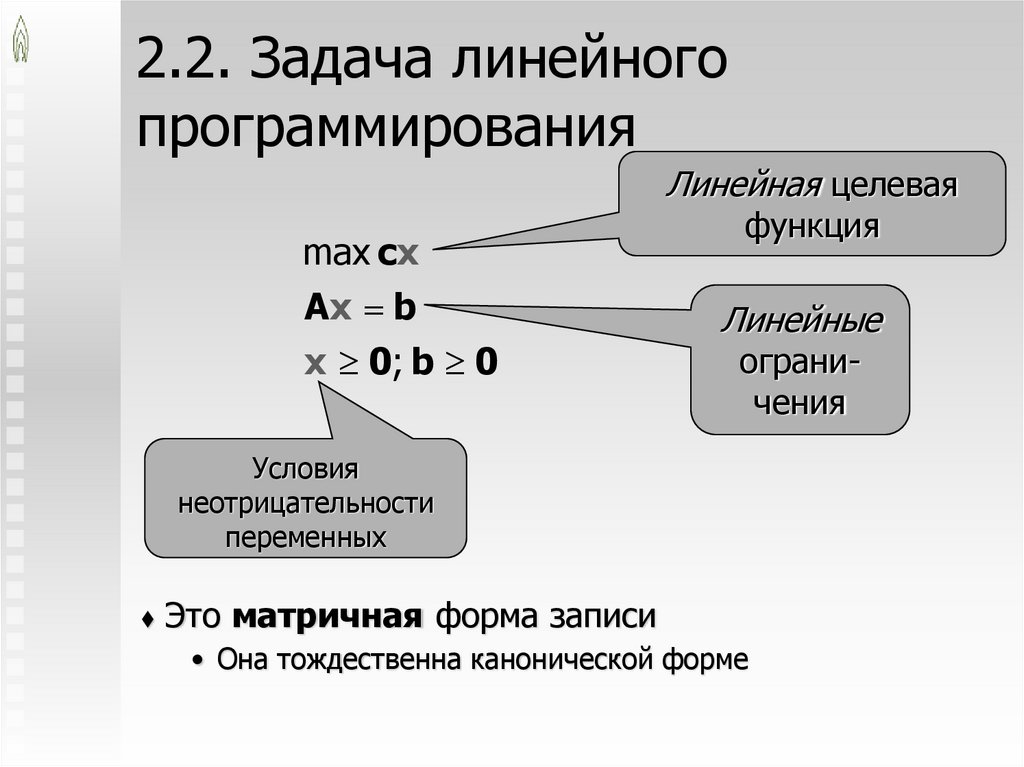
2.2. Задача линейногопрограммирования
Линейная целевая
max cx
Ax b
x 0; b 0
функция
Линейные
ограничения
Условия
неотрицательности
переменных
Это матричная форма записи
• Она тождественна канонической форме
14.
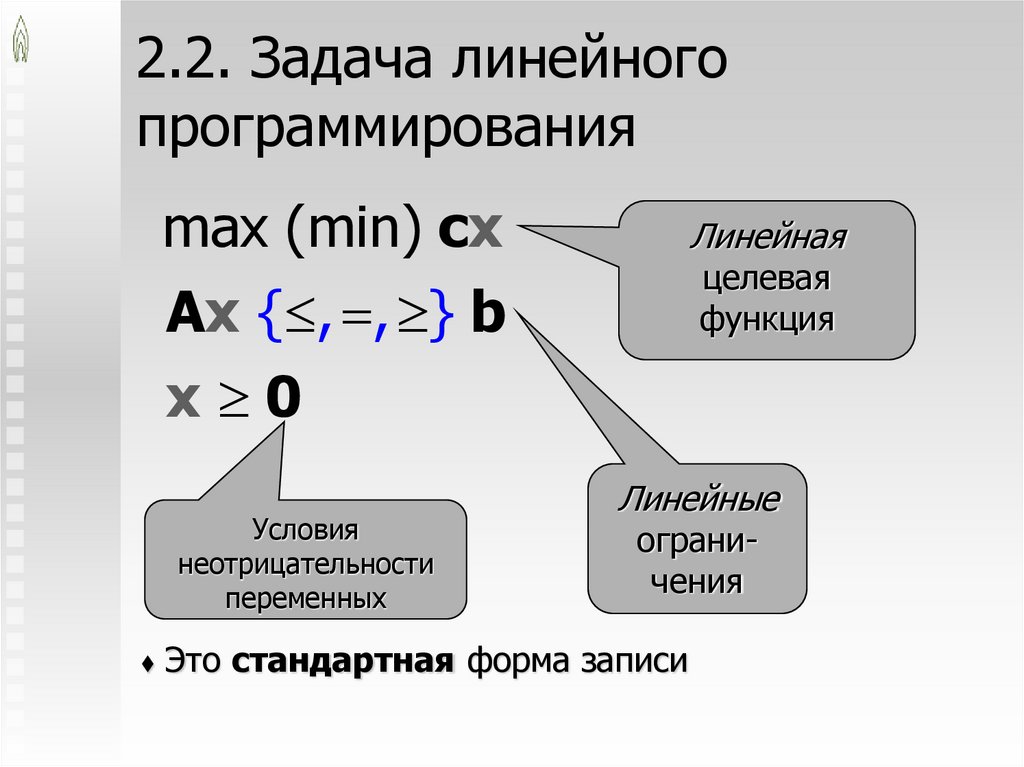
2.2. Задача линейногопрограммирования
max (min) cx
Ax { , , } b
x 0
Условия
неотрицательности
переменных
Линейная
целевая
функция
Линейные
ограничения
Это стандартная форма записи
15.
2.2.Любой вектор x, удовлетворяющий ограничениям
и условиям неотрицательности (безотносительно к
целевой функции), называется допустимым
решением
Если допустимых решений не существует, говорят, что
система ограничений несовместна
Областью допустимых решений (ОДР) называется
множество, включающее все допустимые решения
данной ЗЛП
Допустимое решение x*, доставляющее
наибольшее значение целевой функции среди всех
допустимых решений данной ЗЛП, называется
оптимальным решением
часто его называют просто решением ЗЛП
16.
2.3 Поиск решения как средство решения задачлинейного и нелинейного моделирования
Для решения задачи оптимизации необходимо:
На рабочем листе Excel создать таблицу исходных
данных, в которой должны отображаться формулы. Для
этого необходимо предварительно дать команду Сервис Параметры, выбрать вкладку Вид и установить флажок
Формулы.
Запустить процедуру поиска решения, дав команду
Сервис - Поиск решения, и в появившемся диалоговом
окне Поиск решения заполнить поля:
Установить целевую ячейку:
Изменяя ячейки:
Ограничения:
17.
Целевая ячейка — ячейка на рабочем листе стаблицей исходных данных, куда занесена
формула целевой функции.
Изменяемые ячейки — ячейки из таблицы
исходных данных, отражающие значения
переменных, которые необходимо найти в
результате оптимизации. Ячейки не должны
содержать формулы, их значения должны влиять
на значение целевой ячейки.
Ограничения - задаются посредством кнопки
Добавить и отражают связь формул ограничений
с их свободными членами. Ограничения могут
быть как скалярными (например, A1<=3;
A2<=A3, где A1, A2, A3 — имена ячеек Excel), так
и векторными (например, A1:A10>=B1:B10, где
A1:A10, B1:B10 — диапазоны ячеек).
18.
Задача 1 (линейная модель).Продукцией молочного завода являются молоко, кефир и сметана. На
производство 1 т молока, кефира и сметаны требуется соответственно
1,01; 1,01; 9,45 т молока.
Затраты рабочего времени при разливе 1 т молока и кефира составляют
0,17 и 0,18 машино-час. Расфасовка 1 т сметаны на специальном
автомате занимает 3,15 час. Всего за сутки молочный завод может
переработать 140 т молока.
Основное оборудование может быть занято в течение 21,0 машино-часа,
а автомат по расфасовке сметаны - в течение 16 час. Прибыль от
реализации 1т молока, кефира и сметаны соответственно равна 31, 23 и
137 руб. Завод должен производить ежедневно не менее 90 т молока в
сутки.
Требуется:
1. Определить объемы выпуска молочной продукции каждого вида,
позволяющие получить наибольшую прибыль;
2. Проанализировать, как изменится прибыль, если автомат по разливу
сметаны будет работать на 4 часа меньше, а основное оборудование - на
1 машино-час больше;
3. Определить, как изменится оптимальное решение, если установить
задание по выпуску кефира в объеме не менее 10 т.
19.
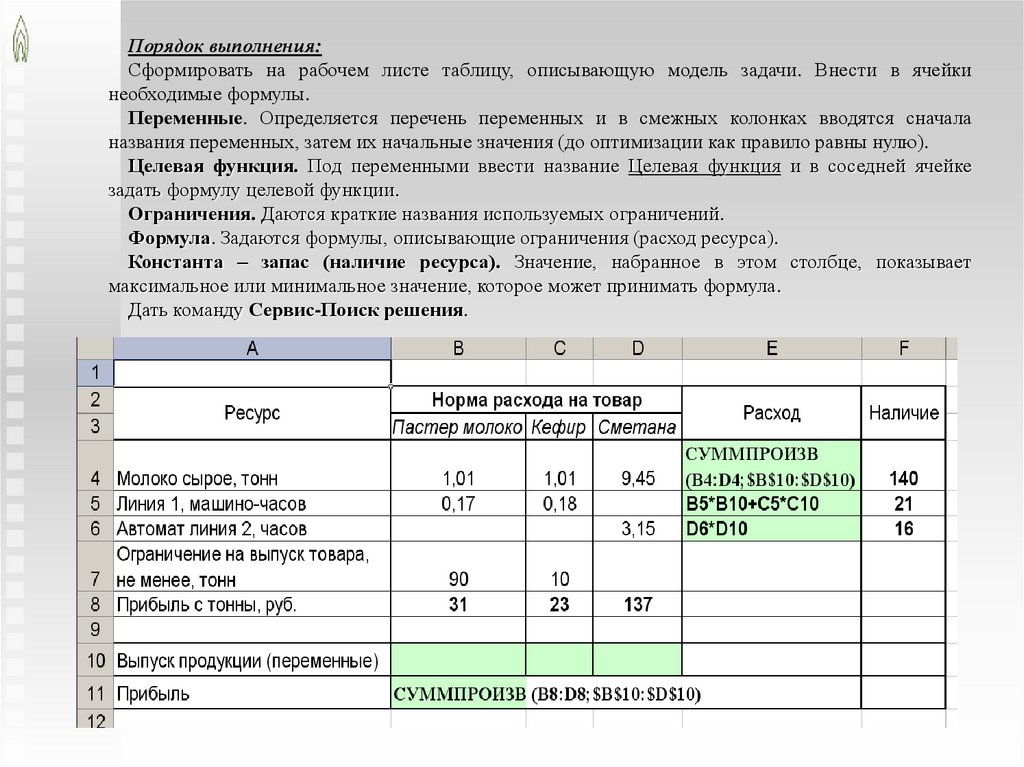
Порядок выполнения:Сформировать на рабочем листе таблицу, описывающую модель задачи. Внести в ячейки
необходимые формулы.
Переменные. Определяется перечень переменных и в смежных колонках вводятся сначала
названия переменных, затем их начальные значения (до оптимизации как правило равны нулю).
Целевая функция. Под переменными ввести название Целевая функция и в соседней ячейке
задать формулу целевой функции.
Ограничения. Даются краткие названия используемых ограничений.
Формула. Задаются формулы, описывающие ограничения (расход ресурса).
Константа – запас (наличие ресурса). Значение, набранное в этом столбце, показывает
максимальное или минимальное значение, которое может принимать формула.
Дать команду Сервис-Поиск решения.
20.
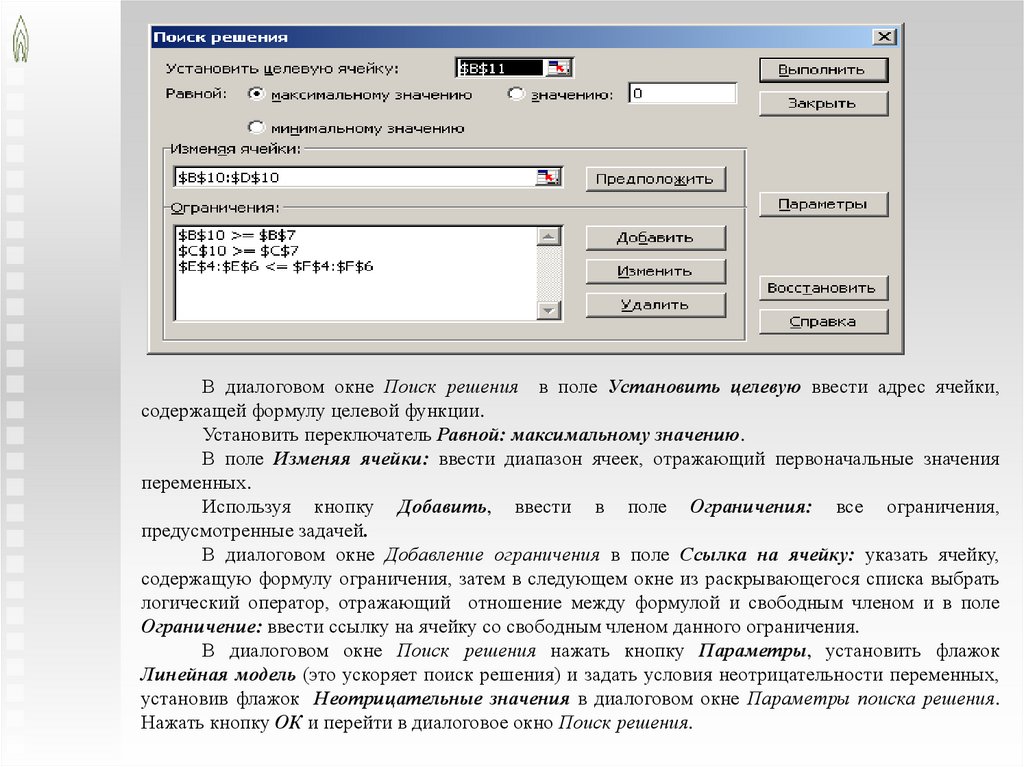
В диалоговом окне Поиск решения в поле Установить целевую ввести адрес ячейки,содержащей формулу целевой функции.
Установить переключатель Равной: максимальному значению.
В поле Изменяя ячейки: ввести диапазон ячеек, отражающий первоначальные значения
переменных.
Используя кнопку Добавить, ввести в поле Ограничения: все ограничения,
предусмотренные задачей.
В диалоговом окне Добавление ограничения в поле Ссылка на ячейку: указать ячейку,
содержащую формулу ограничения, затем в следующем окне из раскрывающегося списка выбрать
логический оператор, отражающий отношение между формулой и свободным членом и в поле
Ограничение: ввести ссылку на ячейку со свободным членом данного ограничения.
В диалоговом окне Поиск решения нажать кнопку Параметры, установить флажок
Линейная модель (это ускоряет поиск решения) и задать условия неотрицательности переменных,
установив флажок Неотрицательные значения в диалоговом окне Параметры поиска решения.
Нажать кнопку ОК и перейти в диалоговое окно Поиск решения.
21.
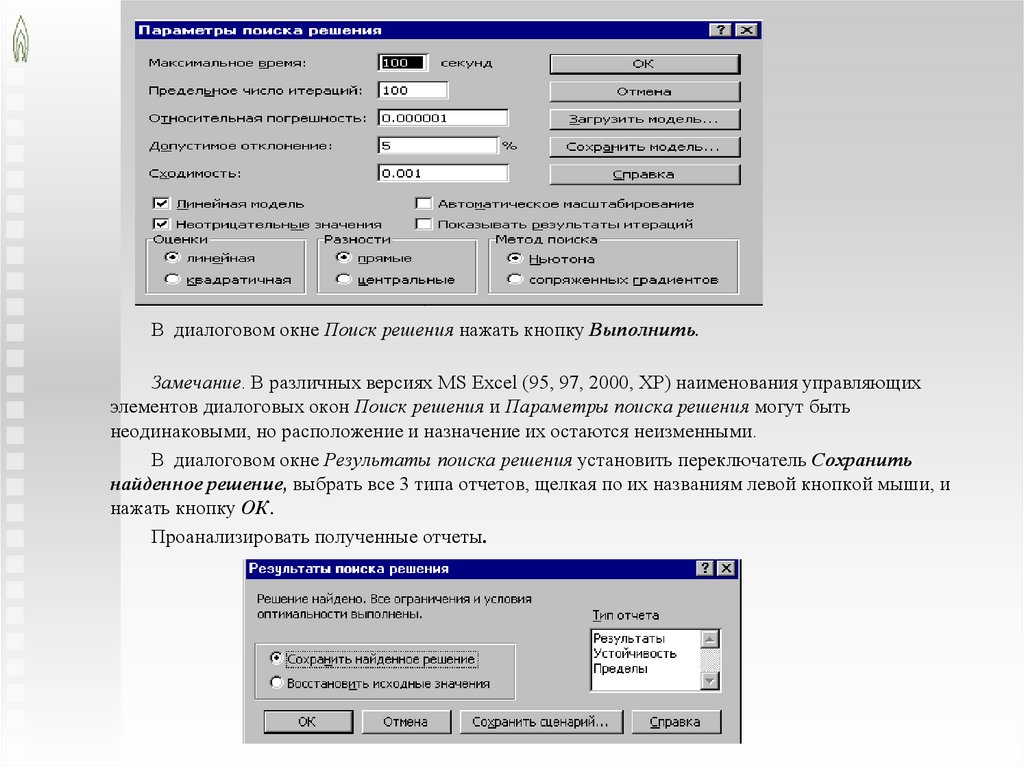
В диалоговом окне Поиск решения нажать кнопку Выполнить.Замечание. В различных версиях MS Excel (95, 97, 2000, XP) наименования управляющих
элементов диалоговых окон Поиск решения и Параметры поиска решения могут быть
неодинаковыми, но расположение и назначение их остаются неизменными.
В диалоговом окне Результаты поиска решения установить переключатель Сохранить
найденное решение, выбрать все 3 типа отчетов, щелкая по их названиям левой кнопкой мыши, и
нажать кнопку ОК.
Проанализировать полученные отчеты.
22.
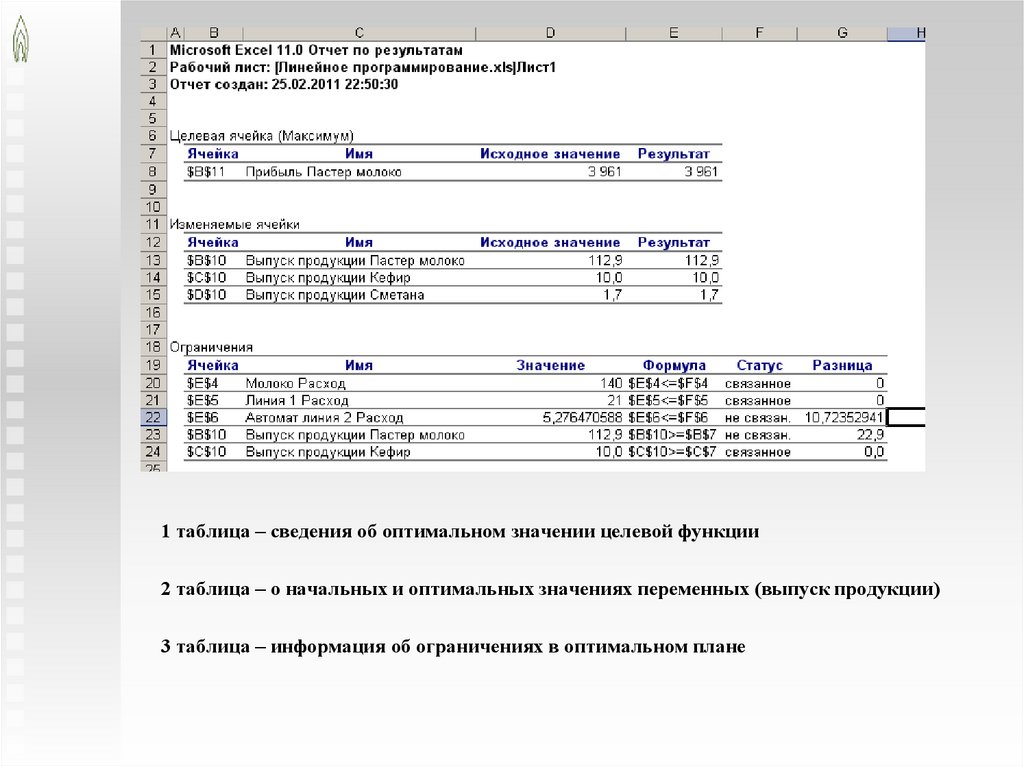
1 таблица – сведения об оптимальном значении целевой функции2 таблица – о начальных и оптимальных значениях переменных (выпуск продукции)
3 таблица – информация об ограничениях в оптимальном плане
23.
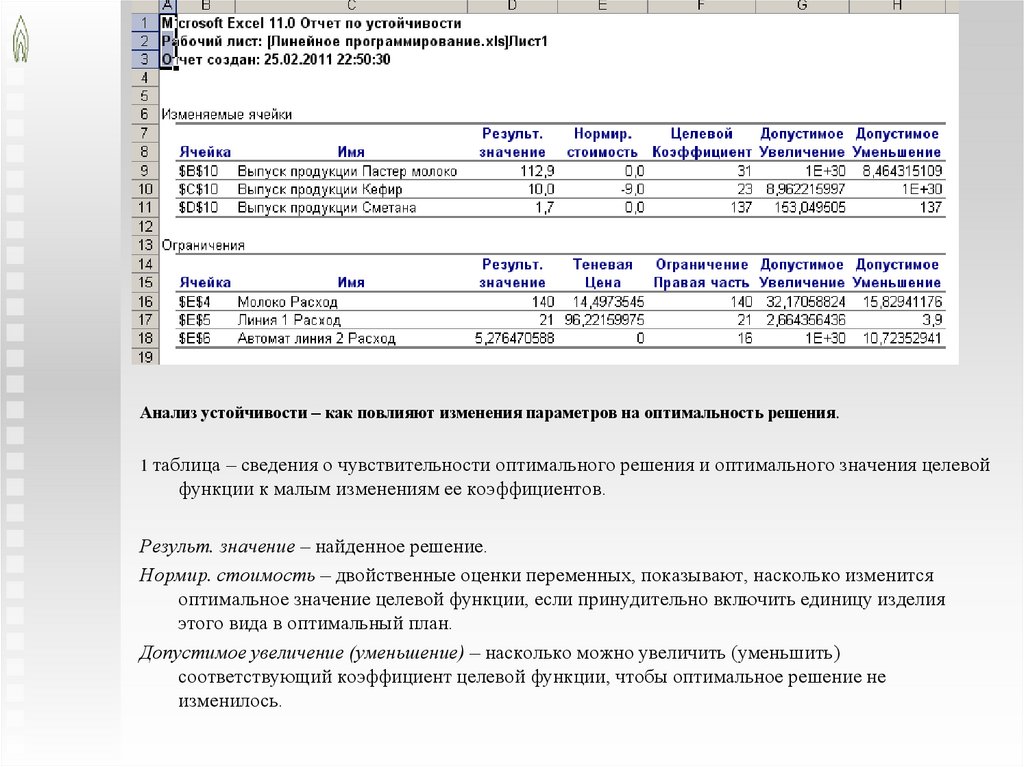
Анализ устойчивости – как повлияют изменения параметров на оптимальность решения.1 таблица – сведения о чувствительности оптимального решения и оптимального значения целевой
функции к малым изменениям ее коэффициентов.
Результ. значение – найденное решение.
Нормир. стоимость – двойственные оценки переменных, показывают, насколько изменится
оптимальное значение целевой функции, если принудительно включить единицу изделия
этого вида в оптимальный план.
Допустимое увеличение (уменьшение) – насколько можно увеличить (уменьшить)
соответствующий коэффициент целевой функции, чтобы оптимальное решение не
изменилось.
24.
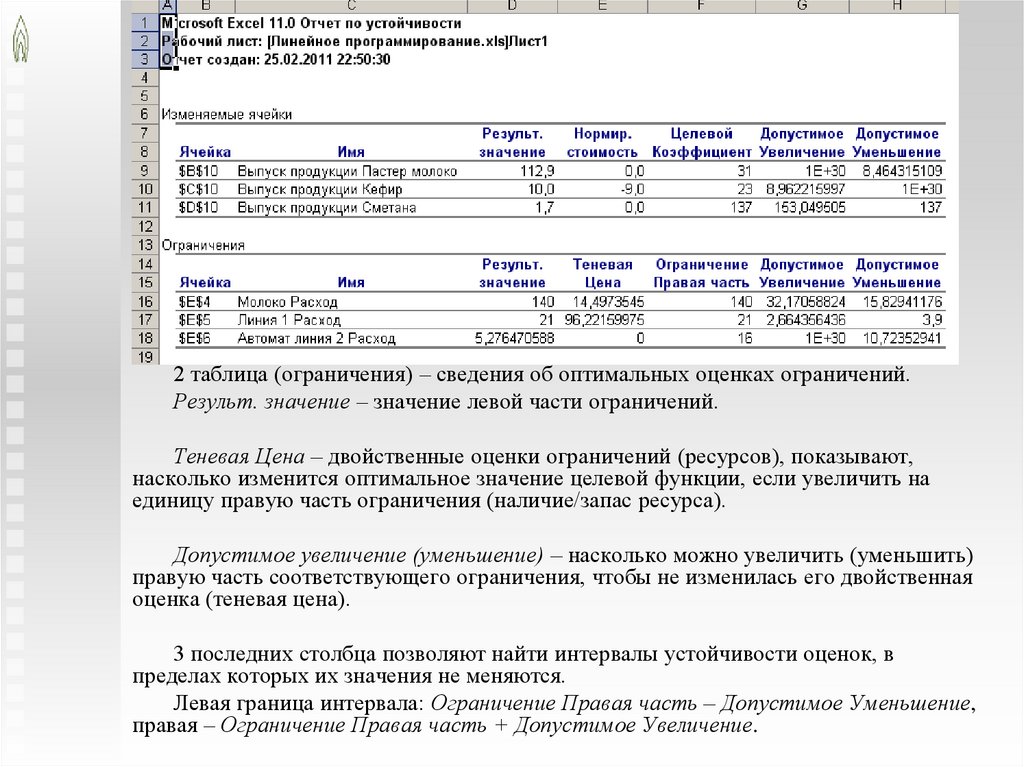
2 таблица (ограничения) – сведения об оптимальных оценках ограничений.Результ. значение – значение левой части ограничений.
Теневая Цена – двойственные оценки ограничений (ресурсов), показывают,
насколько изменится оптимальное значение целевой функции, если увеличить на
единицу правую часть ограничения (наличие/запас ресурса).
Допустимое увеличение (уменьшение) – насколько можно увеличить (уменьшить)
правую часть соответствующего ограничения, чтобы не изменилась его двойственная
оценка (теневая цена).
3 последних столбца позволяют найти интервалы устойчивости оценок, в
пределах которых их значения не меняются.
Левая граница интервала: Ограничение Правая часть – Допустимое Уменьшение,
правая – Ограничение Правая часть + Допустимое Увеличение.
25.
2. Транспортные задачии задачи о назначениях
Содержание лекции:
1.
2.
3.
Формулировка транспортной задачи
Особенности решения открытой транспортной
задачи
Задача о назначениях
26.
ЛитератураЭкономико-математические методы и прикладные
модели: Учеб. пособие для вузов / Под ред. В.В.
Федосеева. — 2-е изд. М.: ЮНИТИ-ДАНА, 2005. —
раздел 3.2.
Фомин Г.П. Математические методы и модели в
коммерческой деятельности: Учебник. – 2-е изд.
М.: Финансы и статистика, 2005. — раздел 2.2.6.
Вентцель Е.С. Исследование операций: Задачи,
принципы, методология. М.: Высшая школа, 2001.
27.
Формулировка транспортнойзадачи
Дано:
Множество I, включающее m пунктов отправления груза,
имеющегося в количествах ai (i=1…m)
Множество J, включающее n пунктов потребления, в
каждом из которых имеется спрос на данный груз в
количестве bj (j=1…n)
Затраты cij на перевозку единицы груза между пунктами i
иj
Найти:
План перевозок X = (xij), согласно которому груз из
пунктов отправления перевозится в пункты потребления
с минимальными издержками, а спрос удовлетворяется
полностью
Обычно предполагается, что общий размер запасов груза равен
спросу (закрытая транспортная задача).
При этом условии задача всегда имеет оптимальное решение.
28.
Целевая функция:m
n
min c ij x ij
x ij
i 1 j 1
Условия удовлетворения спроса:
m
x ij b j ,
i
j 1...n
1
Условия полного вывоза груза:
n
x ij a i ,
j
i 1...m
1
Условия неотрицательности:
x ij 0,
i 1...m , j 1...n
29.
Особенности решения открытойтранспортной задачи
Если спрос больше запасов,
вводят фиктивного
поставщика, располагающего
недостающим количеством
груза
Транспортная задача
называется открытой,
если не выполняется
условие равенства
запасов спросу
• Стоимость «перевозки груза»
от фиктивного поставщика
принимается равным потерям,
возникающих из-за
неудовлетворённого спроса
• «Перевозки» от фиктивного
поставщика
интерпретируются как
величины
неудовлетворённого спроса
соответствующих
потребителей
Если имеется избыточный
запас у поставщиков,
вводят фиктивного
потребителя,
потребляющего избыток
• Стоимость перевозки груза
фиктивному потребителю
принимается равной потерям
при хранении либо нулю
• «Перевозки» фиктивному
потребителю
интерпретируются как
остатки на складах
30.
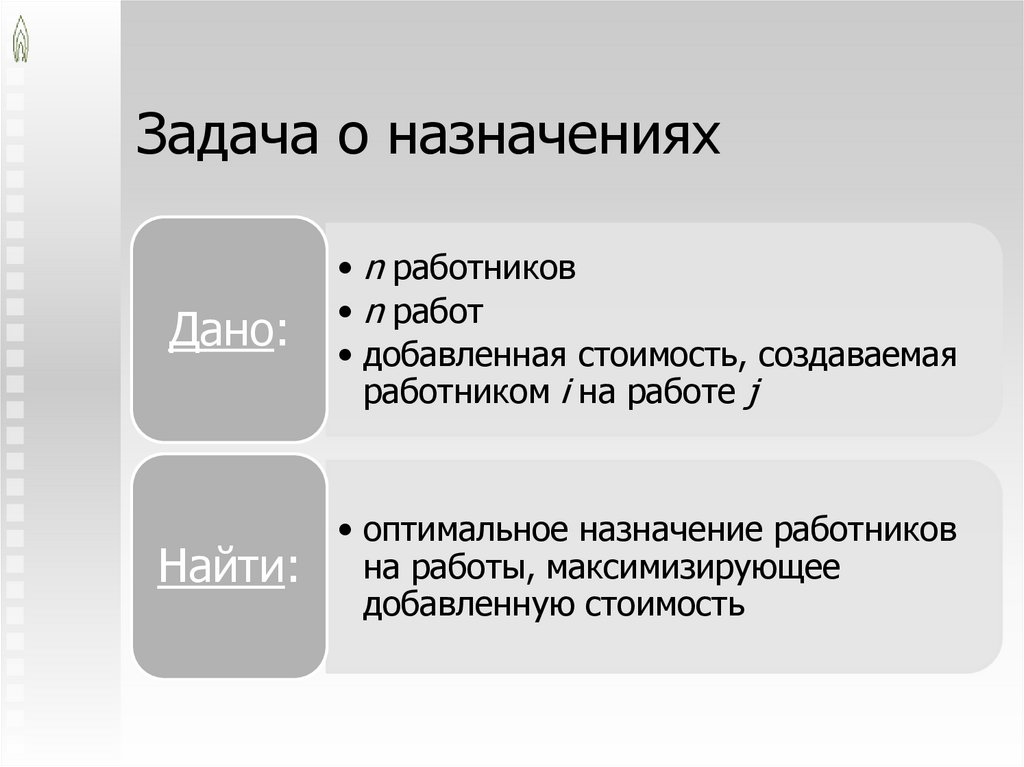
Задача о назначенияхДано:
• n работников
• n работ
• добавленная стоимость, создаваемая
работником i на работе j
Найти:
• оптимальное назначение работников
на работы, максимизирующее
добавленную стоимость
31.
Переформулируется в транспортную задачу последующему правилу:
имеется n поставщиков, располагающих
единичными ресурсами
работники
имеется n потребителей с единичным спросом
работы
стоимость перевозок равна добавленной стоимости,
взятой со знаком «минус»
это делается для того, чтобы добавленная стоимость
максимизировалась
«Перевозки единичного объёма груза»
интерпретируются как назначение работника i
на работу j
Все базисные переменные в этом случае могут
принимать только единичные значения
32.
Пример транспортной задачиУголь, добываемый в нескольких
месторождениях, отправляется ряду
потребителей. Известно, сколько угля
добывается в каждом из месторождений и
сколько его требуется каждому из
потребителей. Известны расстояния между
месторождениями и потребителями, а также
условия сообщения между ними. Учитывая
эти данные, подсчитать, во что обходится
перевозка каждой тонны угля из любого
месторождения в любой пункт потребления.
Требуется при этих условиях спланировать
перевозки угля таким образом, чтобы
затраты на них были минимальными.
33.
Пусть для простоты заданы всего 4 месторождения М1,М2, М3, М4, причем их ежемесячная добыча составляет a1,
а2, а3, а4 тонн угля. Предположим далее, что этот уголь надо
доставить в пункты потребления b1, b2, b3, b4, b5,
соответственно с ежемесячными потребностями этих
пунктов. Будем считать, что общее производство угля равно
суммарной потребности в нем (сбалансированность планов):
a1, а2, а3, а4 = b1, b2, b3, b4, b5. Задача состоит в определении
такого плана перевозок, при котором общая стоимость
перевозок была бы наименьшей. Обозначим через x11
количество угля (в тоннах), предназначенное к отправлению
из M1 в П1; вообще через xij обозначим количество угля,
отправляемого из месторождения Mi в пункт потребления
Пj.
34.
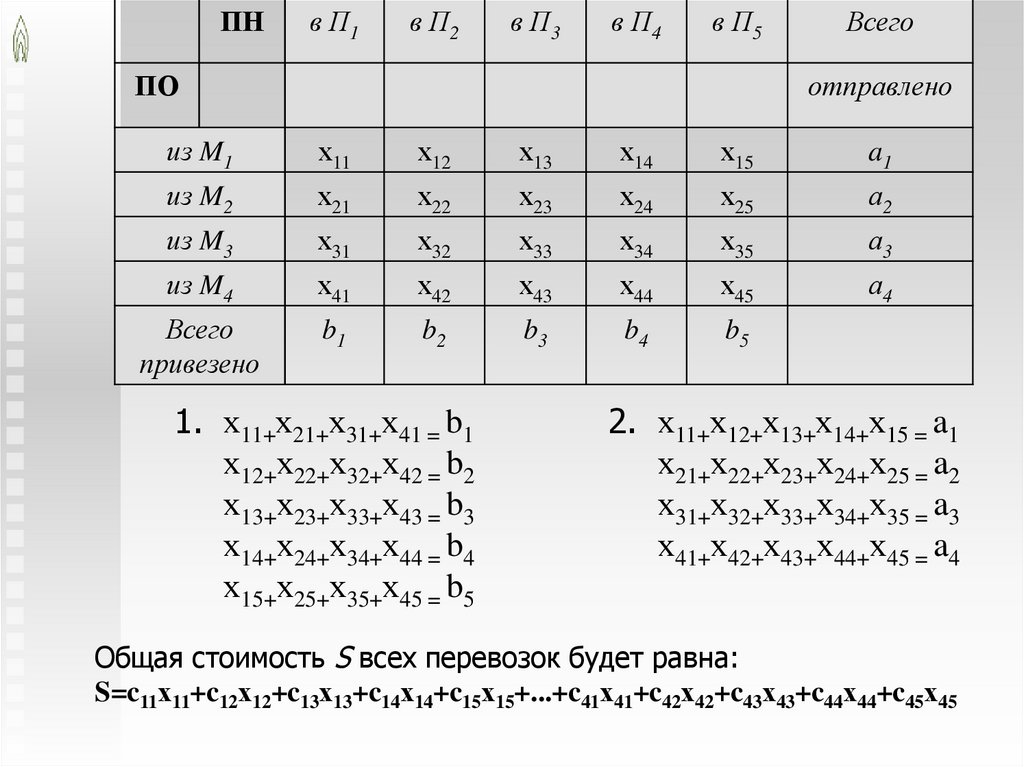
ПНв П1
в П2
в П3
в П4
в П5
ПО
Всего
отправлено
из M1
х11
х12
х13
х14
х15
a1
из M2
х21
х22
х23
х24
х25
а2
из M3
х31
х32
х33
х34
х35
а3
из M4
х41
х42
х43
х44
х45
а4
Всего
привезено
b1
b2
b3
b4
b5
1. х11+х21+х31+х41 = b1
х12+х22+х32+х42 = b2
х13+х23+х33+х43 = b3
х14+х24+х34+х44 = b4
х15+х25+х35+х45 = b5
2. х11+х12+х13+х14+х15 = a1
х21+х22+х23+х24+х25 = a2
х31+х32+х33+х34+х35 = a3
х41+х42+х43+х44+х45 = a4
Общая стоимость S всех перевозок будет равна:
S=c11х11+c12х12+c13х13+c14х14+c15х15+...+c41х41+c42х42+c43х43+c44х44+c45х45






















 mathematics
mathematics








