Вычислительная математика. Введение. Основные понятия и определения

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Вычислительная математика»
Тема «Введение. Основные понятия и
определения»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2013

2. Определение

Вычислительная математика –
раздел математики, изучающий круг
вопросов, связанных с применением
вычислительной техники и численных
методов при решении практических
задач.
Курс «Вычислительная математика»
Тема «Введение»
2

3. Трудности реализации численных методов

1)
Достаточно большая размерность n →число операций
достигает такой огромной величины, что выполнение
всех этих операций становится невозможным даже на
самых мощных ЭВМ.
Для решения СЛАУ из n уравнений
методом Крамера требуется выполнить порядка n*n!
операций,
методом Гаусса требуется выполнить порядка n^3
операций.
2)
Большое число операций → от каждой операции
накапливается вычислительная погрешность →
результат слишком далек от истинного решения.
Курс «Вычислительная математика»
Тема «Введение»
3

4. Численный метод решения задачи

Численный метод решения задачи – это
определенная последовательность
операций над числами, то есть
вычислительный алгоритм, язык которого –
числа и арифметические действия.
Курс «Вычислительная математика»
Тема «Введение»
4

5. Пример реализации численного метода

Требуется найти решение уравнения
x^2 – a = 0, a > 0,
(1)
Зададимся каким–либо начальным
приближением x0 (например, х0=1) и будем
последовательно с помощью формулы:
(2)
вычислять значения х1, х2, …Прервем этот
процесс на некотором n = N и полученное в
результате xN объявим приближенным
решением исходной задачи (1), то есть
положим
Курс «Вычислительная математика»
Тема «Введение»
5

6. Пример реализации численного метода

Докажем, что наш алгоритм (2)
удовлетворяет этому условию.
Положим
(3)
Разделим равенство (2) на
и
подставим в него (3), получим
откуда
(4)
Курс «Вычислительная математика»
Тема «Введение»
6

7. Пример реализации численного метода

Так как
>0, то из
последнего равенства
следует, что все Ɛ , начиная с
первого, положительны.
А значит,
<1.
Курс «Вычислительная математика»
Тема «Введение»
7

8. Пример реализации численного метода

Используя это, получаем из (4):
<
(5)
то есть убывает с ростом n быстрее,
чем геометрическая прогрессия со
знаменателем . Следовательно, xN
→
при n → ∞
(6)
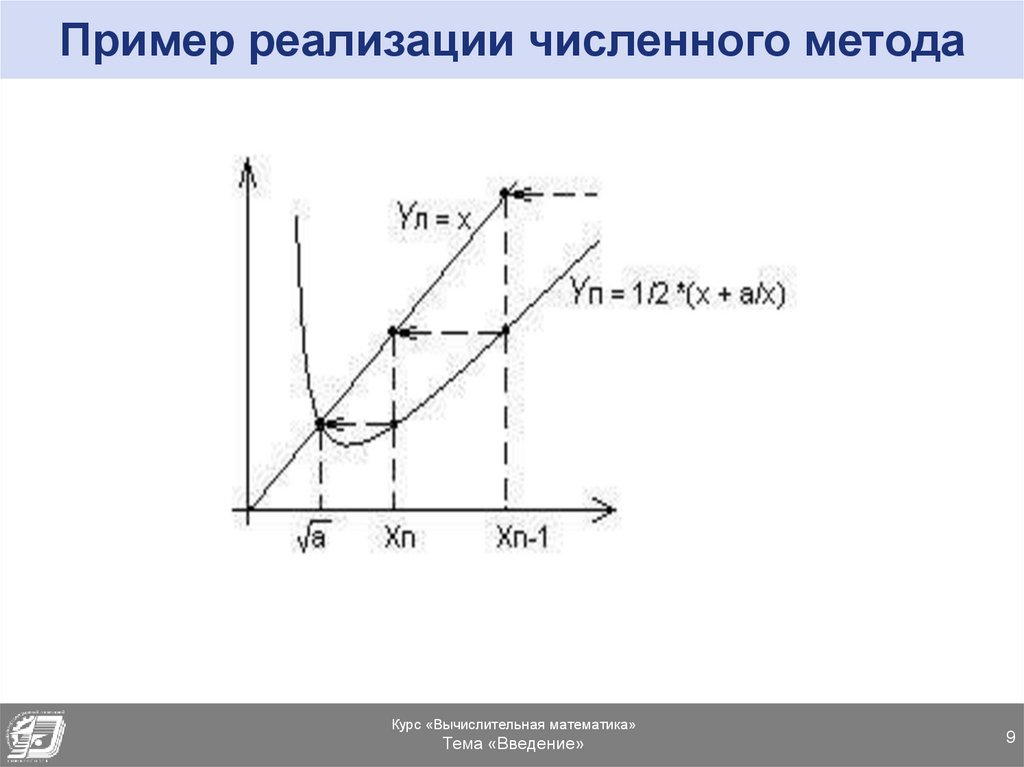
На рисунке показан итерационный
процесс (2).
Здесь даны графики левой yл(х) и
правой yп(х) частей (2).
Курс «Вычислительная математика»
Тема «Введение»
8

9. Пример реализации численного метода

Курс «Вычислительная математика»
Тема «Введение»
9

10. Пример реализации численного метода

Так как yл(√а )=yп(√а ), то эти
графики пересекаются в точке х =
√а .
Проведение итераций по формуле
(2) эквивалентно движению по
изображенной на рисунке
ломаной линии→
итерационный процесс сходится к
√а при N → ∞.
Курс «Вычислительная математика»
Тема «Введение»
10

11. Свойства численных методов

1. Исходная задача (1) заменяется
другой задачей – вычислительным
алгоритмом (2).
2. Задача (2) содержит параметр N,
которого нет в исходной задаче.
3. Выбором этого параметра N можно
добиться любой близости решения (2) к
решению (1), то есть хN к √а .
4. Неточная реализация алгоритма,
вызванная округлениями, не меняет его
свойств.
Курс «Вычислительная математика»
Тема «Введение»
11

12. Классификация погрешностей

1. Погрешности задачи –
погрешности, связанные с самой
постановкой задачи.
Математические формулировки
неточно отображают реальные
явления→ получаем
идеализированные модели.
Эти погрешности неустранимы.
Курс «Вычислительная математика»
Тема «Введение»
12

13. Классификация погрешностей

2. Погрешность метода.
Решить задачу в точной
постановке трудно→ ее заменяют
близкой по результатам
приближенной задачей.
Это устранимые погрешности.
Курс «Вычислительная математика»
Тема «Введение»
13

14. Классификация погрешностей

3.Остаточная погрешность –
погрешность, связанная с наличием
бесконечных процессов в математическом
анализе.
Функции, фигурирующие в математических
формулах, часто задаются в виде
бесконечных последовательностей или
рядов.
Курс «Вычислительная математика»
Тема «Введение»
14

15. Классификация погрешностей

4. Погрешность действий.
Производя вычисление над
приближенными числами,
погрешности входных данных мы
переносим в результат вычислений.
Это неустранимые погрешности.
В дальнейшем мы будем учитывать
погрешности типа 2), 5).
Курс «Вычислительная математика»
Тема «Введение»
15

16. Классификация погрешностей

5. Погрешность округления –
погрешность, связанная с системой
исчисления.
При изображении даже рациональных
чисел в 10 системе исчисления
справа от запятой может быть
бесконечное число цифр (например,
бесконечная десятичная
периодическая дробь).
Курс «Вычислительная математика»
Тема «Введение»
16

17.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2013
© Исенбаева Елена Насимьяновна, 2013