Логические функции

1.

Глава 3. Логические функции
§ 3.1. Основные
понятия
1) Логические функции
Логическая функция f(x1,x2, … ,xn)
– n-арная операция на множестве
B = {0, 1}, т.е. функция f: Bn B
Множество всех логических
функций - P2
Множество всех логических функций n
переменных - P2(n)

2.

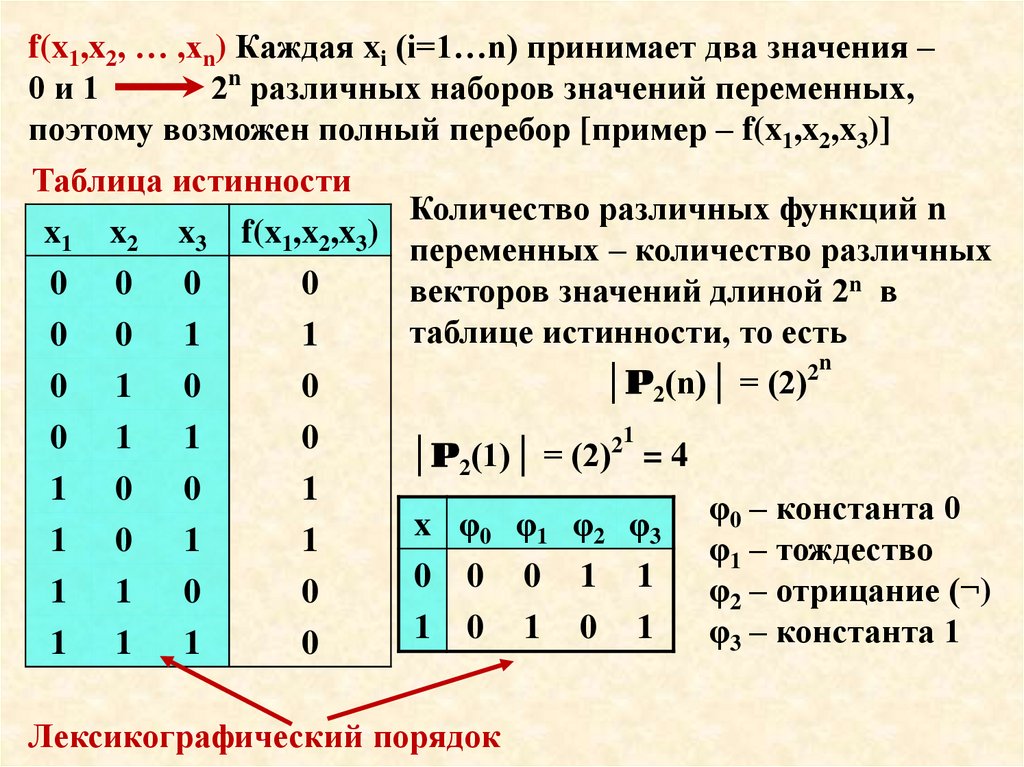
f(x1,x2, … ,xn) Каждая xi (i=1…n) принимает два значения –
0и1
2n различных наборов значений переменных,
поэтому возможен полный перебор [пример – f(x1,x2,x3)]
Таблица истинности
Количество различных функций n
x1 x2 x3 f(x1,x2,x3)
переменных – количество различных
0 0
0
0
векторов значений длиной 2n в
таблице истинности, то есть
0 0
1
1
2n
│P2(n)│ = (2)
0 1
0
0
0
1
1
1
0
0
1
0
1
0
1
1
│P2(1)│ = (2) = 4
1
1
1
1
0
1
0
0
0
1
21
x φ0 φ1 φ2 φ3
0
0
Лексикографический порядок
0
1
1
0
1
1
φ0 – константа 0
φ1 – тождество
φ2 – отрицание (¬)
φ3 – константа 1

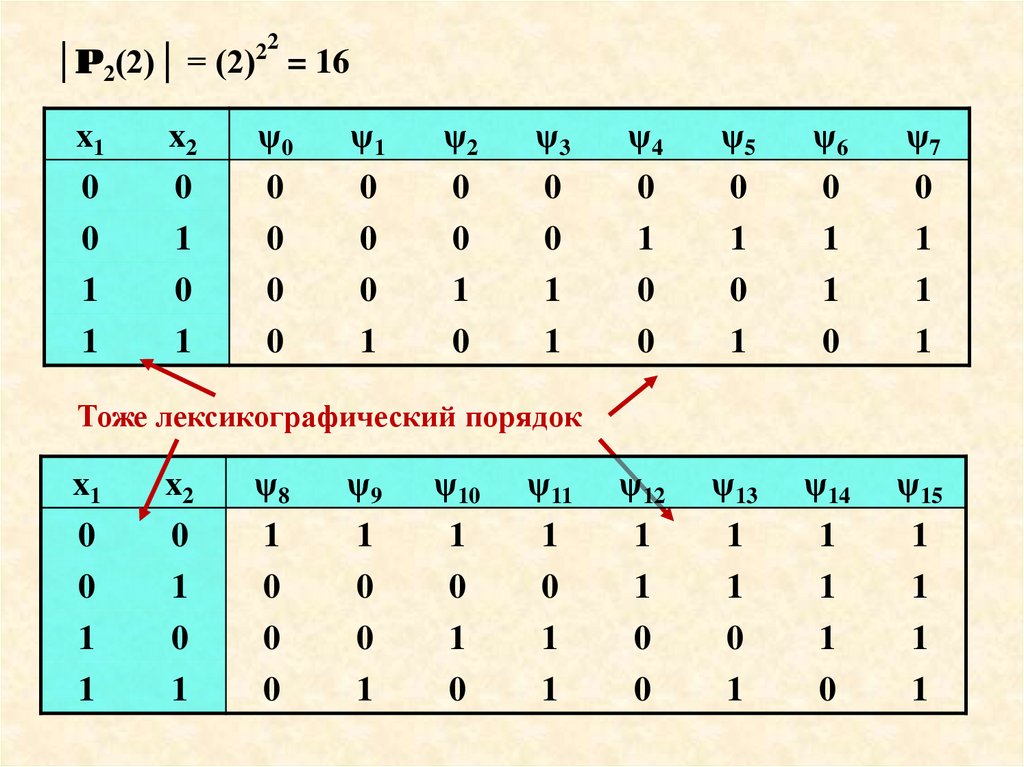
3.

22
│P2(2)│ = (2) = 16
x1
0
0
x2
0
1
ψ0
0
0
ψ1
0
0
ψ2
0
0
ψ3
0
0
ψ4
0
1
ψ5
0
1
ψ6
0
1
ψ7
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
0
0
1
1
0
1
1
ψ12
1
1
0
0
ψ13
1
1
0
1
ψ14
1
1
1
0
ψ15
1
1
1
1
Тоже лексикографический порядок
x1
0
0
1
1
x2
0
1
0
1
ψ8
1
0
0
0
ψ9
1
0
0
1
ψ10
1
0
1
0
ψ11
1
0
1
1

4.

23
│P2(3)│ = (2) = 256
x1
x2
x3
0
1
2
.
.
.
253 254 255
0
0
0
0
0
0
.
.
.
1
1
1
0
0
1
0
0
0
.
.
.
1
1
1
0
1
0
0
0
0
.
.
.
1
1
1
0
1
1
0
0
0
.
.
.
1
1
1
1
0
0
0
0
0
.
.
.
1
1
1
1
0
1
0
0
0
.
.
.
1
1
1
1
1
0
0
0
1
.
.
.
0
1
1
1
1
1
0
1
0
.
.
.
1
0
1
И вновь лексикографический порядок
P2 = P2 (n) – счётное множество (см. § 1.5)
n N
Сравним: вещественные функции на [0, 1] - гиперконтинуум

5.

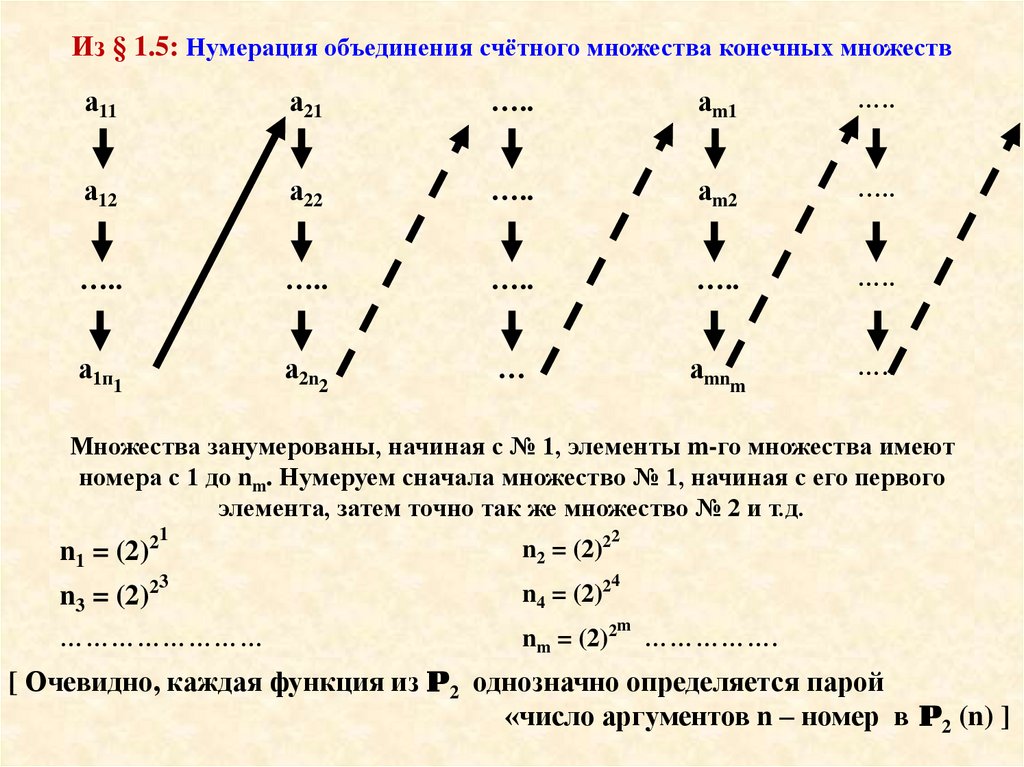
Из § 1.5: Нумерация объединения счётного множества конечных множеств
а11
а21
…..
аm1
…..
а12
а22
…..
аm2
…..
…..
…..
…..
…..
…..
а1п1
а2n2
…
аmnm
…..
Множества занумерованы, начиная с № 1, элементы m-го множества имеют
номера с 1 до nm. Нумеруем сначала множество № 1, начиная с его первого
элемента, затем точно так же множество № 2 и т.д.
21
n2 = (2)2
3
n4 = (2)2
……………………
nm = (2)2
n1 = (2)
n3 = (2)2
2
4
m
…………….
[ Очевидно, каждая функция из P2 однозначно определяется парой
«число аргументов n – номер в P2 (n) ]

6.

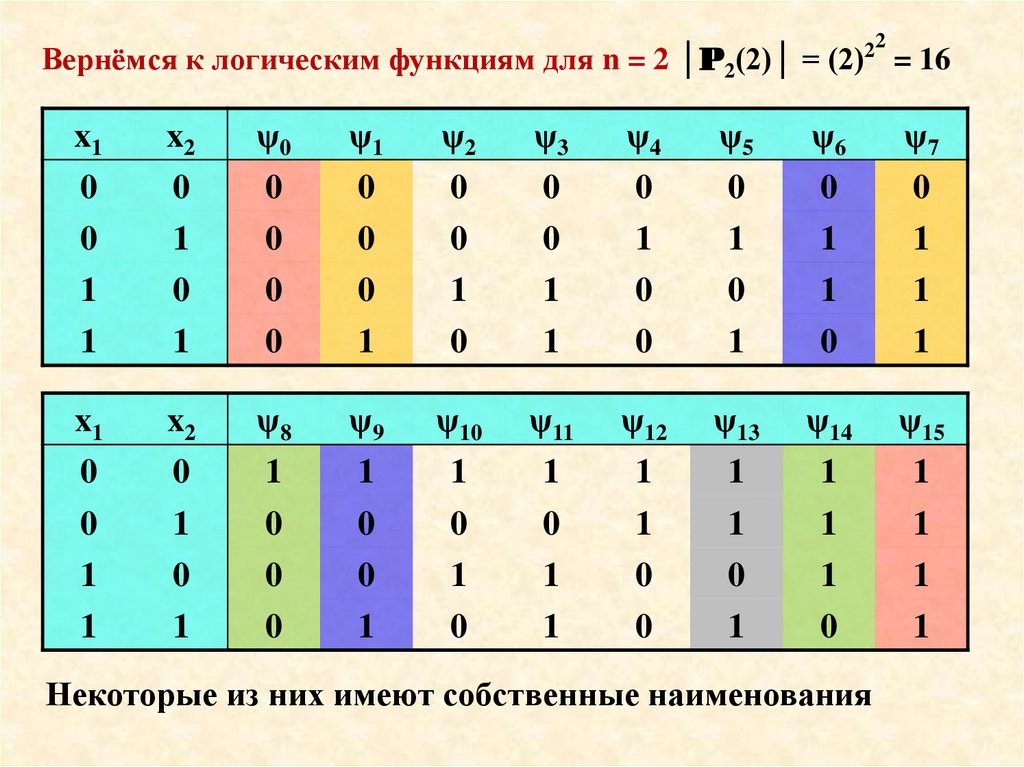
22
Вернёмся к логическим функциям для n = 2 │P2(2)│ = (2) = 16
x1
0
0
x2
0
1
ψ0
0
0
ψ1
0
0
ψ2
0
0
ψ3
0
0
ψ4
0
1
ψ5
0
1
ψ6
0
1
ψ7
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
0
0
1
1
0
1
1
x1
0
x2
0
ψ8
1
ψ9
1
ψ10
1
ψ11
1
ψ12
1
ψ13
1
ψ14
1
ψ15
1
0
1
1
0
0
0
0
0
0
1
0
1
1
0
1
0
1
1
1
1
1
1
0
1
0
1
0
1
0
1
Некоторые из них имеют собственные наименования

7.

ψ0
x1 x2 ψ15
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1
Константы 0 и 1
ψ1
x1 x2
ψ7
ψ1 - конъюнкция, функция
«И», логическое умножение
0
0
0
0
0
0
1
1
0
1
0
1
(x1 & x2, x1 x2, x1 x2)
x1 x2 ψ13
Импликация, функция
«ЕСЛИ – ТО», функция
следования (x1 x2)
ψ8
x1 x2 ψ14
1
0
0
1
0
0
1
1
0
1
0
1
0
1
1
0
0
0
1
0
1
1
1
0
0
1
1
1
1 1 1 1
ψ7 - дизъюнкция, функция
«ИЛИ», логическое
сложение (x1 x2, x1 + x2)
ψ9 - эквивалентность
(x1 x2, x1 x2)
ψ8 - стрелка Пирса (x1 x2)
ψ14 – штрих Шеффера (x1│x2)
ψ6
x1 x2 ψ9
0
0
0
1
ψ6 - неравнозначность,
исключающее «ИЛИ»,
сложение по mod 2 (x1 x2)
1
0
1
0
1
1
0
0
0
1
1
1

8.

Переменная xi в функции f (x1, x2, … ,xi-1, xi, xi+1, … , xn) называется
фиктивной переменной, если выполняется равенство
f (x1, x2, … ,xi-1, 0, xi+1, … , xn) = f (x1, x2, … ,xi-1, 1, xi+1, … , xn)
при любых значениях переменных x1, x2, … ,xi-1, xi+1, … , xn
Если f (x1, x2, … ,xi-1, xi, xi+1, … , xn) = g (x1, x2, … ,xi-1, xi+1, … , xn) при
любых значениях переменных x1, x2, … ,xi-1, xi+1, … , xn, то говорят:
- функция g получена из f удалением фиктивной переменной xi
- функция f получена из g введением фиктивной переменной xi
Сравним: f(x,y) = Sin(x2 + y2 – y2) = Sin(x2) = g(x)
Логические функции f и g называются равными, если они могут
быть получены друг из друга удалением или введением (возможно,
неоднократным) фиктивной переменной
[Очевидно из определения логической функции: не имеет смысла говорить о
равенстве логических функций одинакового числа переменных]

9.

Примеры фиктивных переменных и равных логических функций
ψ5
x1 x2 ψ10
0
0
0
1
1
0
1
0
0
1
0
1
1
1
1
0
ψ5 и ψ10 фиктивно зависят от x1
ψ5(x1,x2) = x2 = φ1(x2) ψ10(x1,x2) = ¬x2 = φ2(x2)
ψ3
x1 x2 ψ12
0
0
0
1
0
0
1
1
1
1
0
0
1
1
1
0
ψ0 и ψ15 фиктивно зависят от x1 и x2
ψ0(x1,x2) = φ0(x1) = φ0(x2) = 0
ψ15(x1,x2) = φ3(x1) = φ3(x2) = 1
ψ3 и ψ12 фиктивно
зависят от x2
ψ3(x1,x2) = x1 = φ1(x1)
ψ12(x1,x2) = ¬x1 = φ2(x1)
ψ0
x1 x2 ψ15
0
0
0
1
0
0
1
1
0
1
0
1
0
1
1
1

10.

2) Логические формулы
Какой-либо класс объектов можно определить:
Определение «через ближайший род и видовое отличие»
B = { x: x A и Р(х) } (класс В состоит из объектов х, принадлежащих А ближайшему роду - и обладающих свойством Р - видовым отличием)
Пример: Логическая функция – n-арная операция на множестве B = {0, 1},
т.е. функция f: Bn B [Минусы: Вспомните, напр., парадокс брадобрея]
Индуктивное (конструктивное, рекурсивное) определение
Определение понятия натурального числа (Джузеппе Пеано):
1. «1» есть натуральное число.
2. Если «п» – натуральное число, то следующее непосредственно за ним
число «n′ » также является натуральным числом.
3. Никаких других натуральных чисел, кроме тех, которые образуются с
помощью правил 1 и 2, нет.
Синтаксис идентификатора в языке программирования
буква ::= a b … z
цифра::= 0 1 … 9
идентификатор::=
<буква> <идентификатор><буква> <идентификатор><цифра>

11.

Логическая формула глубины* k над множеством
логических функций Σ = { f1, f2, … , fm, … }
1. Символы переменных x1, x2, … , xn, … - логические формулы
глубины 0 над (любым) множеством логических функций Σ.
2. Пусть fi ( x1, x2, … , xni ) Σ – n-арная логическая
функция, а F1, F2, … , Fni – логические формулы глубины
не более k над множеством логических функций Σ, причём
хотя бы одна из них имеет глубину ровно k.
Тогда fi ( F1, F2, … , Fni ) – логическая формула глубины
(k+1) над множеством логических функций Σ.
3. Других логических формул над множеством логических
функций Σ нет. (других – т.е. кроме образованных с помощью правил 1 и 2)
В логической формуле fi ( F1, F2, … , Fni ):
F1, F2, … , Fni - подформулы
fi – внешняя (главная) операция формулы
[ * Характеристика «глубина» - возможный параметр индукции – напр. Th.3.1.3]

12.

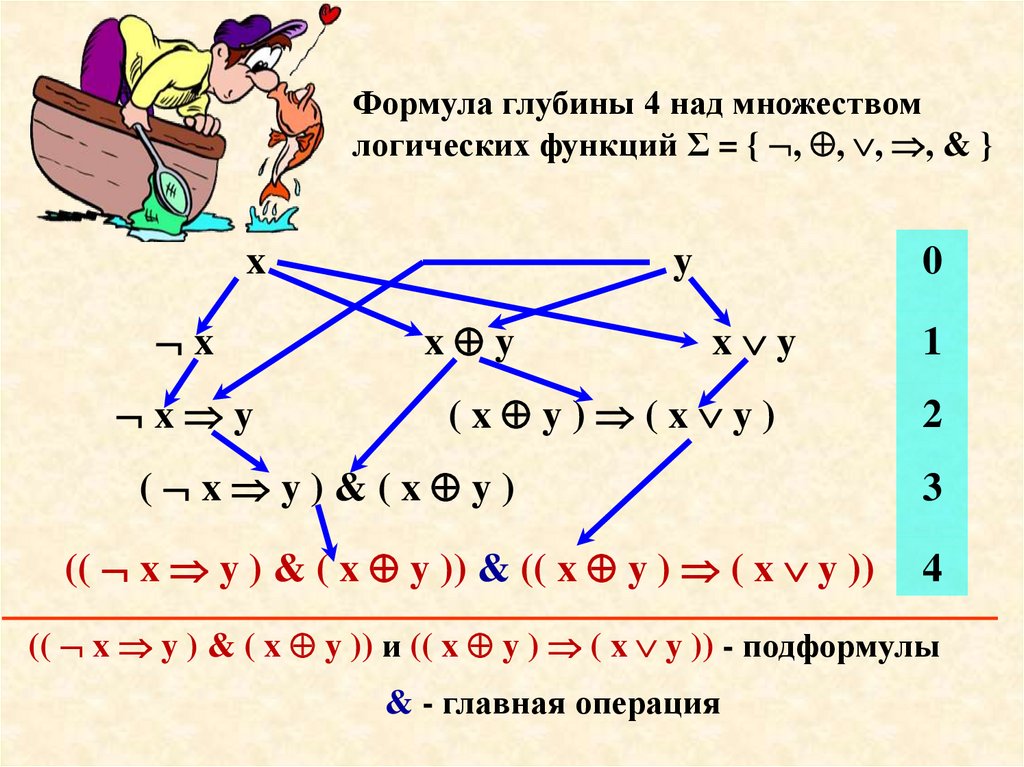
Формула глубины 4 над множеством
логических функций Σ = { , , , , & }
x
x
x y
y
x y
0
x y
1
(x y) (x y)
2
( x y)&(x y)
(( x y ) & ( x y )) & (( x y ) ( x y ))
3
4
(( x y ) & ( x y )) и (( x y ) ( x y )) - подформулы
& - главная операция

13.

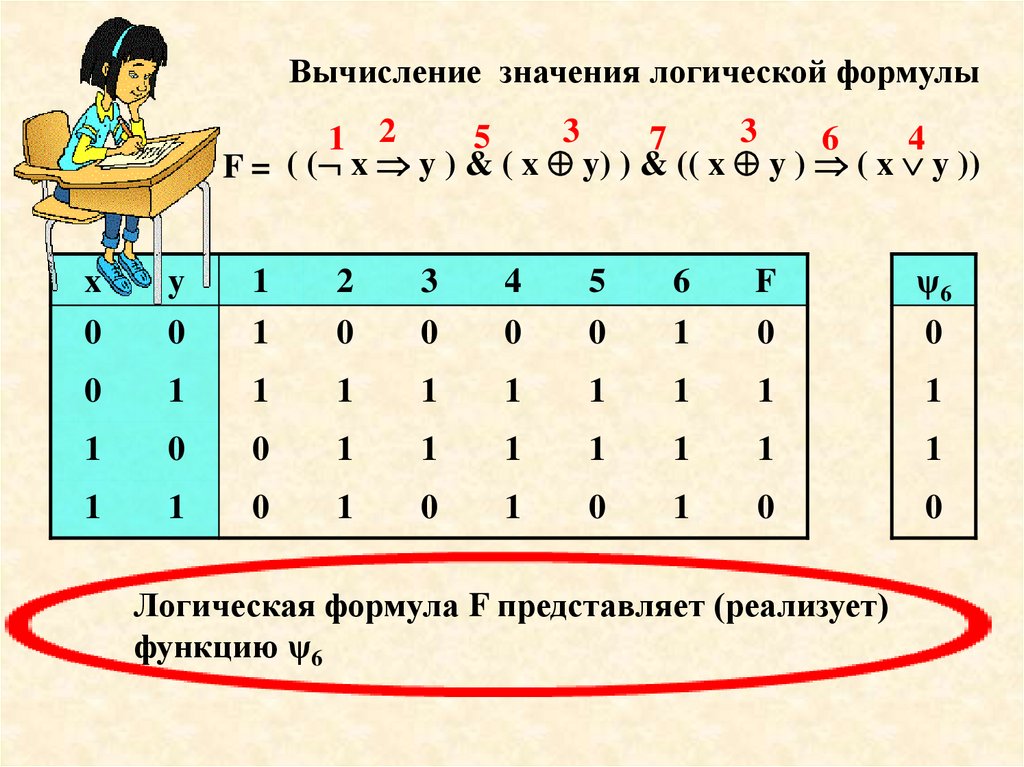
Вычисление значения логической формулы
3
3
5
1 2
7
6
4
F = ( ( x y ) & ( x y) ) & (( x y ) ( x y ))
x
0
y
0
1
1
2
0
3
0
4
0
5
0
6
1
F
0
ψ6
0
0
1
1
1
1
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
0
1
0
1
0
1
0
0
Логическая формула F представляет (реализует)
функцию ψ6

14.

F1 ≈ F2
1
3
2
F1 = ( x y ) ( x y )
2
1
F2 = x ( y x )
x
0
0
y
0
1
1
0
1
2
0
1
F1
1
1
x
0
0
y
0
1
1
1
0
F2
1
1
1
1
0
1
1
0
1
1
1
1
1
1
0
1
1
1
1
1
Логические формулы, представляющие одну и ту же
логическую функцию – эквивалентные (равносильные)
Логическая формула, представляющая константу 1
(φ3, ψ15, η255, …) - тавтология
Логическая формула, представляющая константу 0
(φ0, ψ0, η0, …) - противоречие

15.

Приоритет логических функций
В литературе можно найти
различающиеся утверждения
относительно приоритета
некоторых логических функций.
В учебных пособиях приводится,
например, такой порядок
выполнения действий при
отсутствии скобок. Однако без
сомнений при бесскобочной
записи лучше применять только
зелёные строки из этой таблицы
│
↓
Инверсия, отрицание
&
Конъюнкция
Дизъюнкция
≡
Штрих Шеффера
Стрелка Пирса
Сложение по mod 2
Импликация
Эквивалентность

16.

3) Нормальные формы логических функций
ψ1
x1 x2
ψ7
0
0
0
0
0
0
1
1
0
1
0
1
1
1
1
1
Необходимые сведения для дальнейшего
Конъюнкция 1
Дизъюнкция 7
0&0=0
0&1=0
0 0=0
0 1=1
1&0=0
1&1=1
1 0=1
1 1=1
Если хотя бы один из
аргументов равен 0,
результат конъюнкции
равен 0
Если хотя бы один из
аргументов равен 1,
результат дизъюнкции
равен 1

17.

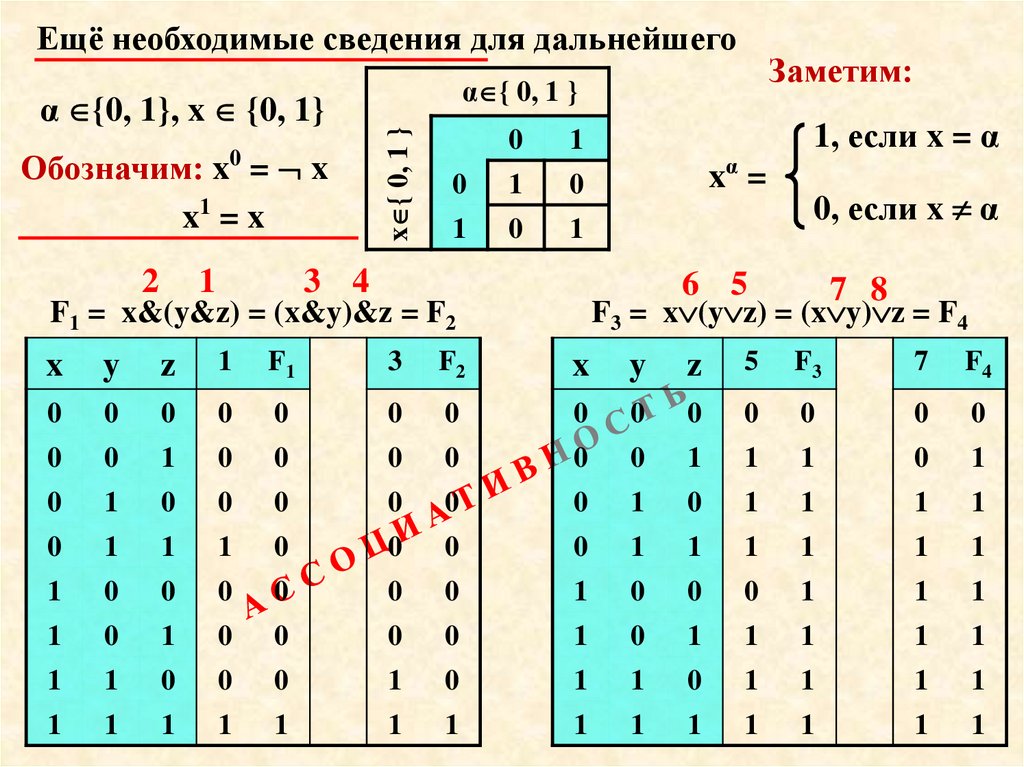
Ещё необходимые сведения для дальнейшего
Обозначим: x = x
x1 = x
0
2
1
x { 0, 1 }
α {0, 1}, x {0, 1}
Заметим:
α { 0, 1 }
0
1
0
1
0
1
0
1
xα =
3 4
1, если x = α
0, если x α
6 5
F1 = x&(y&z) = (x&y)&z = F2
7 8
F3 = x (y z) = (x y) z = F4
x
y
z
1
F1
3
F2
x
y
z
5
F3
7
F4
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
1
0
1
0
1
0
0
0
0
0
0
1
0
1
1
1
1
0
1
1
1
0
0
0
0
1
1
1
1
1
1
1
0
0
0
0
0
0
1
0
0
0
1
1
1
1
0
1
0
0
0
0
1
0
1
1
1
1
1
1
1
0
0
0
1
0
1
1
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1

18.

Всякая логическая функция f (x1, x2, … , xn) может
быть представлена в виде
Th.3.1.1
f (x1, x2, … , xm, xm+1, … , xn) =
=
(x
α ...α
α1
1
1
αm
& … & xm & f (α1, … , αm, xm+1, … , xn))
(▼)
m
Здесь: m n; дизъюнкция берётся по всем 2m наборам
значений параметров α1, … , αm (αi {0, 1}, i = 1…m)
Равенство (▼) – разложение функции f (x1, … , xn) по
переменным x1, … , xm
Формула
α1
αm
(x1 & … & xm & f (α1, … , αm, xm+1, … , xn))
α1...αm
- дизъюнктивная нормальная форма (ДНФ) ф-ии f (x1, … , xn)

19.

Доказательство Th.3.1.1
Подставим в левую и правую части равенства (▼)
произвольный набор значений (σ1, … , σm, σm+1, … , σn):
f (σ1, σ2, … , σm, σm+1, … , σn) =
=
(σ
α ...α
1
α1
1
(▼▼)
αm
& … & σm & f (α1, … , αm, σm+1, … , σn))
m
В правой части (▼▼) присутствуют все 2m конъюнкций - для
каждого из наборов значений α1, … , αm, в том числе ровно одна
такая, что αi = σi для всех i=1…m, т.е. в результате вычисления будет
α1
αm
αi
получено σ1 & … & σm = 1 [так как σi = 1 σi = αi ]
В каждой из остальных (2m- 1) конъюнкций хотя бы для одного
α
значения j=1…m имеет место αj σj, значит, σj j = 0,
α
α
следовательно, σ1 1 & … & σm m = 0
f (x1, x2, … , xm, xm+1, … , xn) =
=
(x
α1...αm
α1
1
α
& … & xm m & f (α1, … , αm, xm+1, … , xn))
(▼)

20.

α
α
В результате вычисления значений σ1 1 & … & σm m для
всех наборов α1...αm равенство (▼▼) принимает вид
f (σ1, σ2, … , σm, σm+1, … , σn) =
α
α
= σ1 1 & … & σm m & f (α1, … , αm, σm+1, … , σn)
а с учётом равенства αi = σi для всех i=1…m и того, что
αi
σi = 1 при σi = αi , получаем:
f (σ1, σ2, … , σm, σm+1, … , σn) =
σ1
σm
& … & σm & f (σ1, … , σm, σm+1, … , σn) =
= σ1
= f (σ1, σ2, … , σm, σm+1, … , σn)
Набор значений (σ1, σ2, … , σm, σm+1, … , σn) – произвольный,
поэтому разложение (▼) доказано
Доказано Th.3.1.1

21.

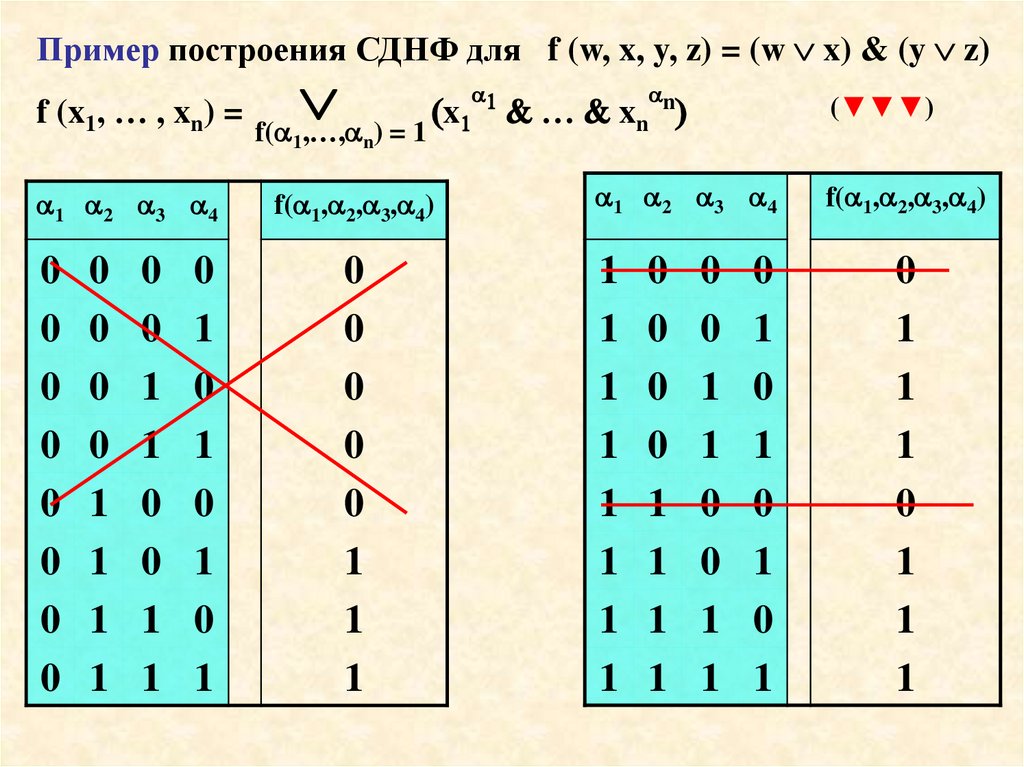
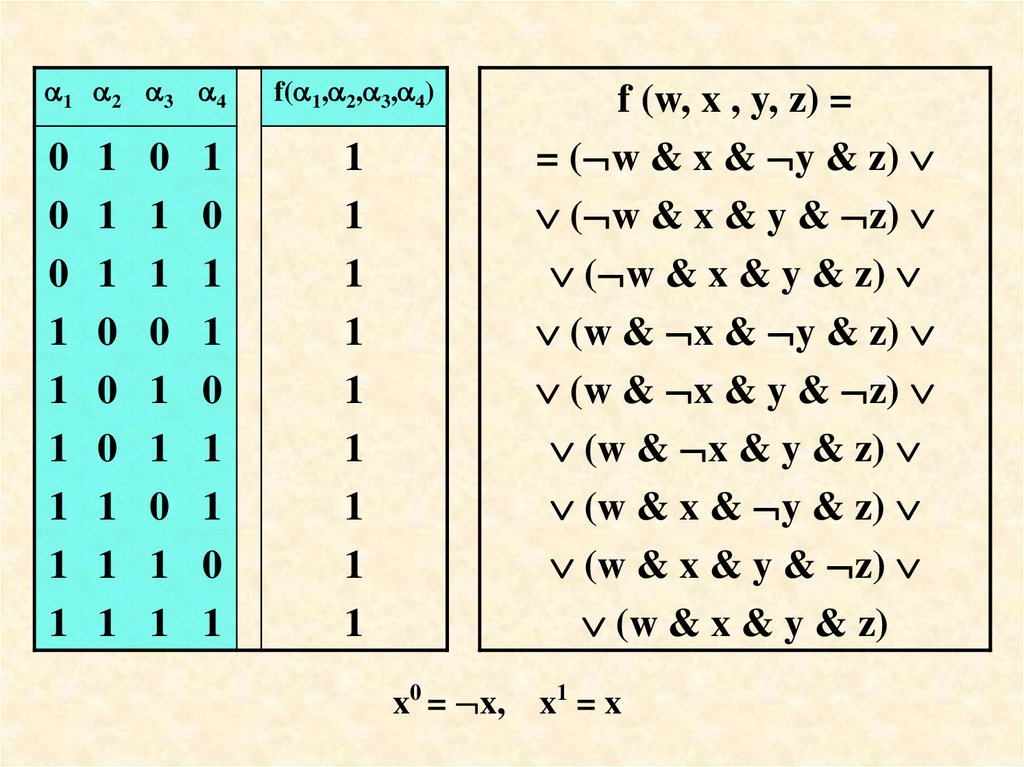
Пример Разложение функции f(w,x,y,z) = (w x) & (y z)
по переменным w и x
(▼): f (w, x, y, z) = α α (w & x & f (α1, α2, y, z))
α1 α2
f (w, x, y, z) =
0
0
1
1
α1
α2
1 2
x0 = x
x1 = x
( w & x & f (0, 0, y, z))
( w & x & f (0, 1, y, z))
(w & x & f (1, 0, y, z))
(w & x & f (1, 1, y, z))
0
1
0
1
Таким образом f (w, x, y, z) = (w x) & (y z) =
= ( w & x & (0 0) & (y z)) ( w & x & (0 1) & (y z))
(w & x & (1 0) & (y z)) (w & x & (1 1) & (y z))
f (x1, x2, … , xm, xm+1, … , xn) =
=
(x
α ...α
1
1
m
α1
α
& … & xm m & f (α1, … , αm, xm+1, … , xn))
(▼)

22.

Итак, доказано:
f (x1, x2, … , xm, xm+1, … , xn) =
α1
αm
= α
(x
&
…
&
x
& f (α1, … , αm, xm+1, … , xn)) (▼)
1
m
...α
1
m
В равенстве (▼) положим m = n:
f (x1, … , xn) =
(x & … & x & f (α , … , α )) =
α ...α
(x & … & x )
(▼▼▼)
=
f( ,…, ) = 1
α1
αn
1
1
n
1
n
n
α1
1
1
αn
n
n
Так как 0 & f(…) = 0, то дизъюнкция берётся по всем наборам
значений параметров ( 1,…, n), для которых выполнено
α1
αn
α1
αn
f( 1,…, n)= 1 и, так как x1 & … & xn & 1 = x1 & … & xn , то
f(α1, … ,αm) опускается.
Равенство (▼▼▼) – совершенная дизъюнктивная
нормальная форма (СДНФ) функции f (x1, … , xn)
Из (▼▼▼) очевидно: не имеет СДНФ единственная функция
– та, для которой
f (x1, … , xn) 0, т.е. константа 0

23.

Процедура построения СДНФ
f (x1, … , xn) =
x { 0, 1 }
{ 0, 1 }
0
1
0
1
0
1
0
1
(x
f( ,…, ) = 1
1
1
n
1
& … & xn n)
(▼▼▼)
СДНФ (▼▼▼) функции f (x1, … , xn)
содержит ровно столько конъюнкций,
сколько единиц в векторе значений
функции f (x1, … , xn)
Было ранее отмечено: x0 = x, x1 = x
i
Если i = 1, в качестве xi принимается xi
i
Если i = 0, в качестве xi принимается xi

24.

Пример построения СДНФ для f (w, x, y, z) = (w x) & (y z)
f (x1, … , xn) =
(x
f( ,…, ) = 1
1 2 3 4
f( 1, 2, 3, 4)
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
n
0
0
0
0
0
1
1
1
1
1
& … & xn n)
(▼▼▼)
1 2 3 4
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
f( 1, 2, 3, 4)
0
1
1
1
0
1
1
1

25.

1 2 3 4
0
0
0
1
1
1
1
1
1
1
1
1
0
0
0
1
1
1
0
1
1
0
1
1
0
1
1
1
0
1
1
0
1
1
0
1
f( 1, 2, 3, 4)
1
1
1
1
1
1
1
1
1
f (w, x , y, z) =
= ( w & x & y & z)
( w & x & y & z)
( w & x & y & z)
(w & x & y & z)
(w & x & y & z)
(w & x & y & z)
(w & x & y & z)
(w & x & y & z)
(w & x & y & z)
x0 = x, x1 = x

26.

Th.3.1.2
Всякая логическая функция f (x1, x2, … , xn) может
быть представлена в виде
f (x1, x2, … , xm, xm+1, … , xn) =
=
& (x1
α1...αm
α1
αm
… xm f (α1, … , αm, xm+1, … , xn))
(▲)
Здесь: m n; конъюнкция берётся по всем 2m наборам
значений параметров α1, … , αm (αi {0, 1}, i = 1…m)
Формула
&
α1...αm
α
α
(x1 1 … xm m f (α1, … , αm, xm+1, … , xn))
- конъюнктивная нормальная форма (КНФ) ф-ии f (x1, … , xn)

27.

Доказательство Th.3.1.2
Подставим в левую и правую части равенства (▲)
произвольный набор значений (σ1, … , σm, σm+1, … , σn):
f (σ1, σ2, … , σm, σm+1, … , σn) =
=
& (σ1
α1...αm
α1
(▲▲)
αm
… σm f (α1, … , αm, σm+1, … , σn))
В правой части (▲▲) присутствуют 2m дизъюнкций, каждая из
которых соответствует набору значений α1, … , αm, в том числе
ровно одна дизъюнкция такая, что αi = σi для всех i=1…m, т.е. в
α1
αm
результате вычисления будет получено σ1 … σm = 0
В каждой из остальных (2m- 1) дизъюнкций хотя бы для
αj
одного значения j=1…m имеет место αj σj, значит, σj = 1,
α1
αm
следовательно, σ1 … σm = 1

28.

α
α
В результате вычисления значений σ1 1 & … & σm m для
всех наборов α1...αm равенство (▲▲) принимает вид
f (σ1, σ2, … , σm, σm+1, … , σn) =
= σ1
α1
αm
… σm f (α1, … , αm, σm+1, … , σn)
а с учётом равенства αi = σi для всех i=1…m и того, что
α
при x = α имеет место x = 0, получаем:
f (σ1, σ2, … , σm, σm+1, … , σn) =
σ1
σm
… σm f (σ1, … , σm, σm+1, … , σn) =
= σ1
= f (σ1, σ2, … , σm, σm+1, … , σn)
Набор значений (σ1, σ2, … , σm, σm+1, … , σn) – произвольный,
поэтому разложение (▲) доказано
Доказано Th.3.1.2

29.

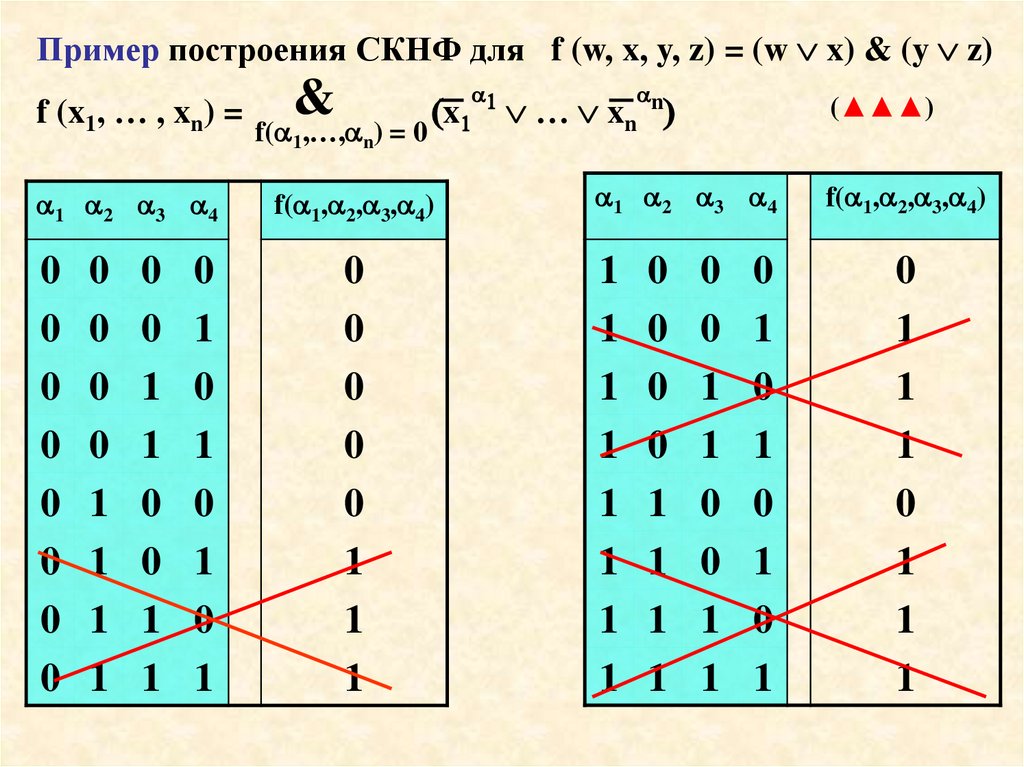
Пример Разложение функции f(w,x,y,z) = (w x) & (y z)
по переменным w и x
(▲): f (w, x, y, z) = α&α (w 1 x 2 f (α1, α2, y, z))
1 2
f (w, x, y, z) =
(w x f (0, 0, y, z)) &
& (w x f (0, 1, y, z)) &
Но теперь
x 1 = x, x 0 = x
& ( w x f (1, 0, y, z)) &
& ( w x f (1, 1, y, z))
α
α
α1 α2
0 0
0 1
1 0
1 1
Как и ранее, f (w, x, y, z) = (w x) & (y z) =
= (w x ((0 0)&(y z))) & (w x ((0 1)&(y z))) &
& ( w x ((1 0)&(y z))) & ( w x ((1 1)&(y z)))

30.

Итак, доказано: f (x1, x2, … , xm, xm+1, … , xn) =
= α&
...α
1
m
α
α
(x1 1 … xm m f (α1, … , αm, xm+1, … , xn))
(▲)
В равенстве (▲) положим m = n:
f (x1, … , xn) =
α1
αn
(x … x f (α , … , α )) =
&
α ...α
(x … x )
(▲▲▲)
=
&
f( ,…, ) = 0
1
1
n
1
n
n
α1
1
1
αn
n
n
Здесь: конъюнкция берётся по всем наборам значений
параметров ( 1,…, n), для которых выполнено f( 1,…, n)= 0
Равенство (▲▲▲) – совершенная конъюнктивная
нормальная форма (СКНФ) функции f (x1, … , xn)
Из (▲▲▲) очевидно: не имеет СКНФ единственная
функция – та, для которой f (x1, … , xn) 1, т.е. константа 1

31.

Пример построения СКНФ для f (w, x, y, z) = (w x) & (y z)
f (x1, … , xn) =
1 2 3 4
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
&
f( 1,…, n) = 0
f( 1, 2, 3, 4)
0
0
0
0
0
1
1
1
(x1 1 … xn n)
(▲▲▲)
1 2 3 4
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
f( 1, 2, 3, 4)
0
1
1
1
0
1
1
1

32.

1 2 3 4
0
0
0
0
0
1
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
0
1
0
1
0
0
0
f( 1, 2, 3, 4)
0
0
0
0
0
0
0
f (w, x , y, z) =
= (w x y z) &
& (w x y z) &
& (w x y z) &
& (w x y z) &
& (w x y z) &
& ( w x y z) &
& ( w x y z)
x 1 = x,
x0=x

33.

4) Функционально полные системы логических функций
Логическая формула глубины k над множеством логических
функций Σ = { f1, f2, … , fm, … }
1. Символы переменных x1, x2, … , xn, … - логические формулы
глубины 0 над (любым) множеством логических функций Σ.
2. Пусть fi ( x1, x2, … , xni ) Σ – n-арная логическая
функция, а F1, F2, … , Fni – логические формулы глубины
не более k над множеством логических функций Σ, причём
хотя бы одна из них имеет глубину ровно k.
Тогда fi ( F1, F2, … , Fni ) – логическая формула глубины
(k+1) над множеством логических функций Σ.
3. Других логических формул над множеством логических
функций Σ нет. (других – т.е. кроме образованных с помощью правил 1 и 2)

34.

Система логических функций Σ называется полной
(функционально полной), если любая логическая функция
может быть представлена логической формулой над Σ
Σ0 = { , &, - функционально полная (см. СДНФ, СКНФ)
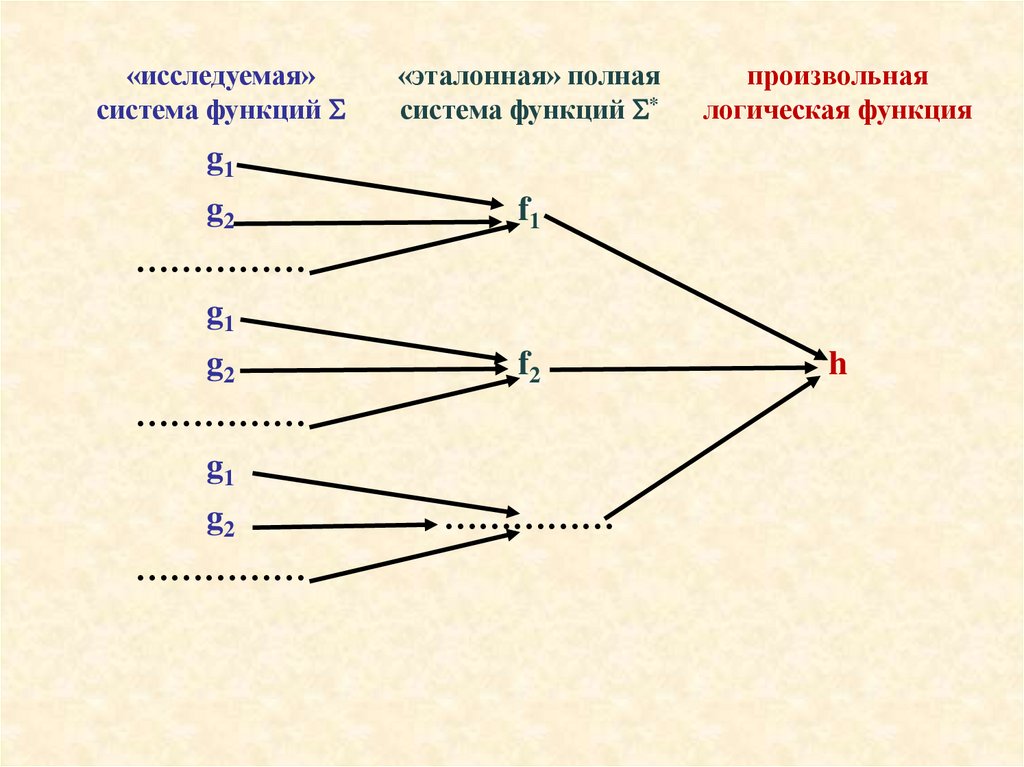
Th.3.1.3
Заданы две системы логических функций:
Σ* = { f1, f2, …
Σ = { g1, g2, …
Система Σ* - функционально полная и любая логическая
функция из Σ* может быть реализована формулой над Σ.
Тогда система Σ – функционально полная

35.

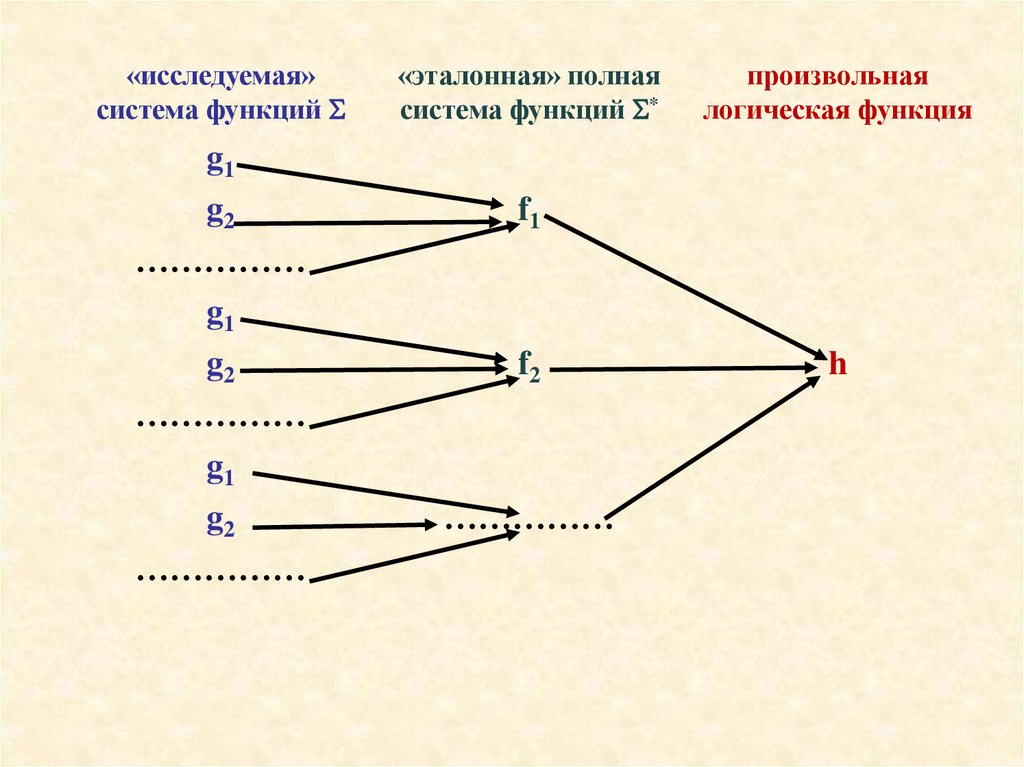
«исследуемая»
система функций
«эталонная» полная
система функций *
произвольная
логическая функция
g1
g2
……………
g1
g2
f1
f2
……………
g1
g2
……………
……………
h

36.

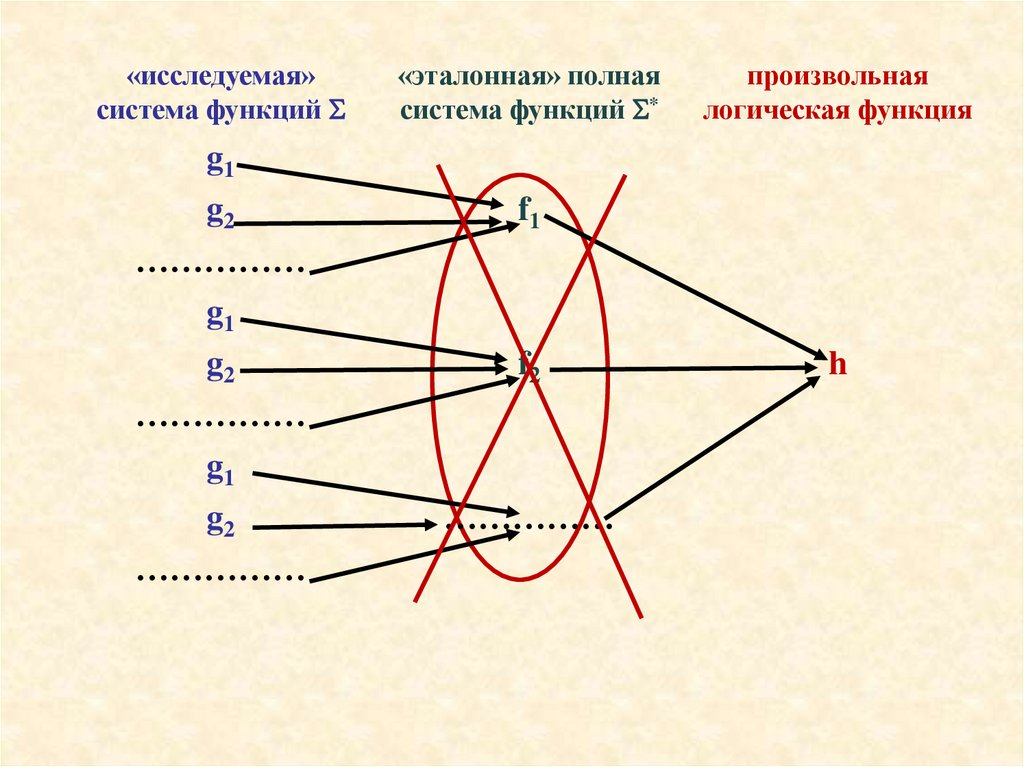
«исследуемая»
система функций
«эталонная» полная
система функций *
произвольная
логическая функция
g1
g2
……………
g1
g2
f1
f2
……………
g1
g2
……………
……………
h

37.

Доказательство Th.3.1.3
Любая h P2 представима h = fi (F1, F2, … , Fni) – формула над Σ*
Здесь: F1, F2, … , Fni – подформулы также над Σ* (по условию)
Далее: Индукция по глубине формулы h = fi (F1, F2, … , Fni)
Глубина = 1
h = fi (xj1, xj2, … , xjn )
i
По условию: любая fi Σ* представима формулой над Σ:
f1 = gk1(g1, g2, … )
…………………………………..
fi = gki (g1, g2, … )
…………………………………..
gki (g1, g2, … ) – представление функции h формулой над Σ, т.е.
для глубины = 1 доказано
[ Арность всех gki, разумеется, конечная. Такая запись, чтобы уйти
от многоэтажных индексов ]

38.

Пусть верно для формул глубины k, т.е. все функции,
представимые над Σ* формулами глубиной не более k,
могут быть реализованы формулами над Σ
h P2
h=fi(F1,F2,…,Fni) – формула над Σ* глубины (k+1)
F1,F2,…,Fni - формулы над Σ* глубины не более k,
т.е. подпадают под индукционное предположение:
h = fi (gj1 (g1, g2, … ), gj2 (g1, g2, … ), … , gjn (g1, g2, … )) =
i
= gki (gj1 (g1, g2, … ), gj2 (g1, g2, … ), … , gjn (g1, g2, … )) ( )
i
( ) - представление функции h формулой над Σ
В силу произвольности h P2
Доказано Th.3.1.3

39.

«исследуемая»
система функций
«эталонная» полная
система функций *
произвольная
логическая функция
g1
g2
……………
g1
g2
f1
f2
……………
g1
g2
……………
……………
h

40.

Пример
Σ0 = { &, , - функционально полная (СДНФ, СКНФ)
Доказать полноту системы Σ1 = { &,
1. Выбираем одну из известных полных систем в
качестве Σ* (пока это только Σ0)
2. Все функции Σ* = { &, , представляем
логическими формулами над Σ1 = { &, :
x & y = Ф1(&, )
Элементарно:
(3.2.8)
x y = Ф2(&, )
x = Ф3(&, )
x & y = Ф1(&, ) = x & y
x = Ф3(&, ) = x
(x y) = x & y
( (x y)) = ( x & y)
x y = ( x & y)
x y = Ф2(&, ) = ( x & y)

41.

Эффективность более удачного выбора Σ*
Доказываем полноту Σ3 = { &, , 1
Кандидаты в Σ*: Σ0 = { &, , и Σ1 = { &,
Если выберем Σ0 в качестве Σ*, то представляем три функции
системы Σ0 = { &, , формулами над Σ3 = { &, , 1 :
2) x = x 1
1) x & y = x & y
3) x y = x y = ( x & y) = ((x 1) & (y 1)) 1
Если выберем Σ1 в качестве Σ*, то представляем лишь две
функции из Σ1 = { &, формулами над Σ3 = { &, , 1 :
1) x & y = x & y
2) x = x 1

42.

Построить представление: x y = (&, , )
x
y
x
y x&y
x y
x y «Исправим» функцию x y путём
0
0
1
1
0
0
0
её умножения (&) на функцию с
0
1
1
0
0
1
1
вектором значений (1,1,1,0) с тем,
1
0
0
1
0
1
1
чтобы у дизъюнкции сохранить
1
1
0
0
1
1
0
значения в первых трёх строках и
изменить на противоположное значение (0) в последней строке. Это
быть, например, функция F(x,y) = (x&y) или,
с учётом правил де Моргана (3.2.8), F(x,y) = x y.
Таким образом, получаем x y = (x y) & ( x y) =
[ (3.2.3) – дистрибутивность конъюнкции относительно дизъюнкции ]
= (x& x) (x& y) (y& x) (y& y) =
[ (3.2.9) – закон противоречия, затем (3.2.7) – свойства констант ]
= 0 (x& y) ( x&y) 0 = (x& y) ( x&y)

43.

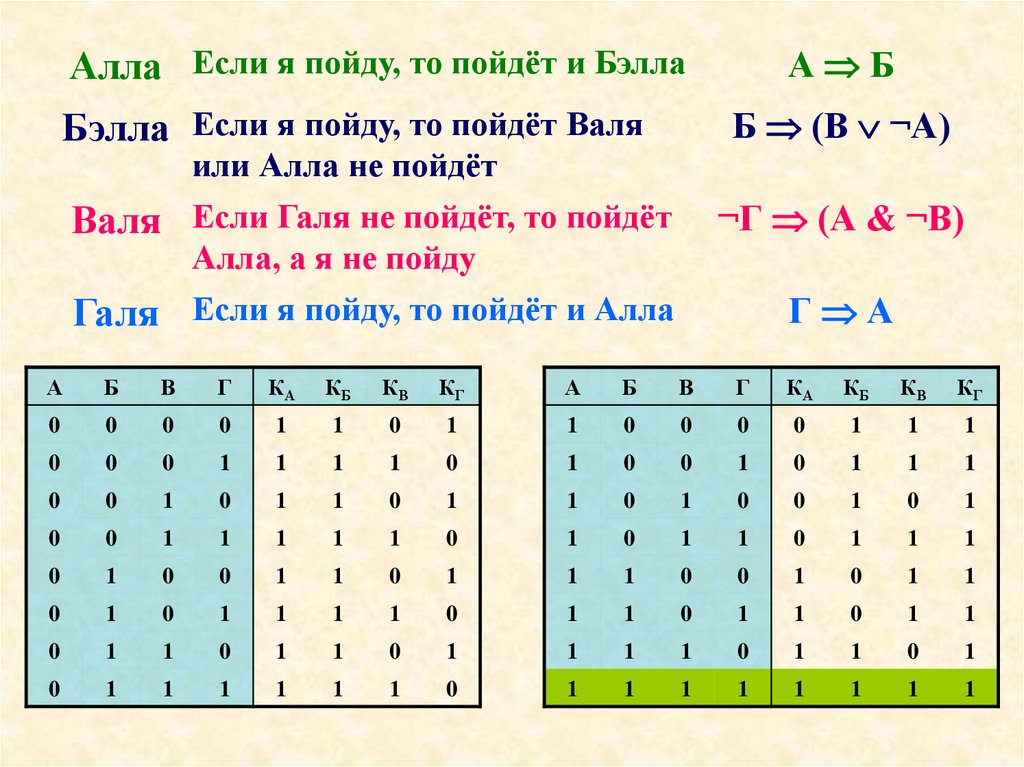
Задача
Девушки собираются в клуб
и, как положено,
капризничают:
Алла: Если я пойду, то пойдёт и
Бэлла
Бэлла: Если я пойду, то пойдёт
Валя или Алла не пойдёт
Валя: Если Галя не пойдёт, то
пойдёт Алла, а я не пойду
Галя: Если я пойду, то пойдёт и
Алла
Смогут ли девушки
договориться или кому-то
придётся уступить ?

44.

Алла Если я пойду, то пойдёт и Бэлла
А Б
Бэлла Если я пойду, то пойдёт Валя
Б (В ¬А)
Валя Если Галя не пойдёт, то пойдёт
¬Г (А & ¬В)
или Алла не пойдёт
Алла, а я не пойду
Галя Если я пойду, то пойдёт и Алла
Г А
А
Б
В
Г
КА
КБ
КВ
КГ
А
Б
В
Г
КА
КБ
КВ
КГ
0
0
0
0
1
1
0
1
1
0
0
0
0
1
1
1
0
0
0
1
1
1
1
0
1
0
0
1
0
1
1
1
0
0
1
0
1
1
0
1
1
0
1
0
0
1
0
1
0
0
1
1
1
1
1
0
1
0
1
1
0
1
1
1
0
1
0
0
1
1
0
1
1
1
0
0
1
0
1
1
0
1
0
1
1
1
1
0
1
1
0
1
1
0
1
1
0
1
1
0
1
1
0
1
1
1
1
0
1
1
0
1
0
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1

45.

Задача
Некая страна населена
жителями, каждый из
которых либо всегда
говорит правду, либо
всегда лжёт. На все
вопросы они отвечают
только «да» и «нет».
К развилке дорог, одна из
которых ведёт в столицу, а другая – не ведёт, подошёл
путешественник, направляющийся в столицу. Указателей на
развилке нет, зато гуляет гражданка, которая согласна
ответить, увы, лишь на один вопрос…...
Какой вопрос ей задать, чтобы правильно выбрать путь
в столицу ?

46.

Интерпретация логической
переменной
Значения переменной
x
Гражданка всегда говорит правду
1 - да
0 - нет
y
Чтобы попасть в столицу, нужно
пойти по дороге в левую сторону
1 - да
0 - нет
Вопрос: верно ли, что f(x,y) = 1? Мы хотим получить ответ
«да» тогда и только тогда, когда дорога в левую сторону
действительно приведёт в столицу
x
y
Желаемый ответ на вопрос
Необходимое значение f(x,y)
0
0
1
0
1
0
Нет
Да
Нет
1
0
0
1
1
Да
1
Итак, спросим: верно ли, что ψ9 (x,y) [x y, x y] равно 1