Similar presentations:
Интеллектуальный анализ данных (Data Mining)
1.
Интеллектуальный анализ данных(Data Mining)
Арефьева Е.А.
1
Арефьева Е.А. ИИС
2.
ИНТЕЛЛЕКТУАЛЬНЫЙ АНАЛИЗ ДАННЫХОбучающая выборка :
Инструментарии
"с учителем", когда для
нейронные сети;
каждого примера задается в
явном виде значение
признака его
принадлежности
некоторому классу
ситуаций
(классообразующего
признака);
-"без учителя", когда по
степени близости значений
признаков классификации
система сама выделяет
классы ситуаций.
2
Арефьева Е.А. ИИС
деревья решений,
индукция,
кластеризация,
эволюционное
моделирование,
нечеткая логика,
визуализация данных
и т.д.
3.
ТИПЫ ЗАКОНОМЕРНОСТЕЙАссоциация
Прогнозирование
Последовательность
Типы
Кластеризация
3
Арефьева Е.А. ИИС
Классификация
4.
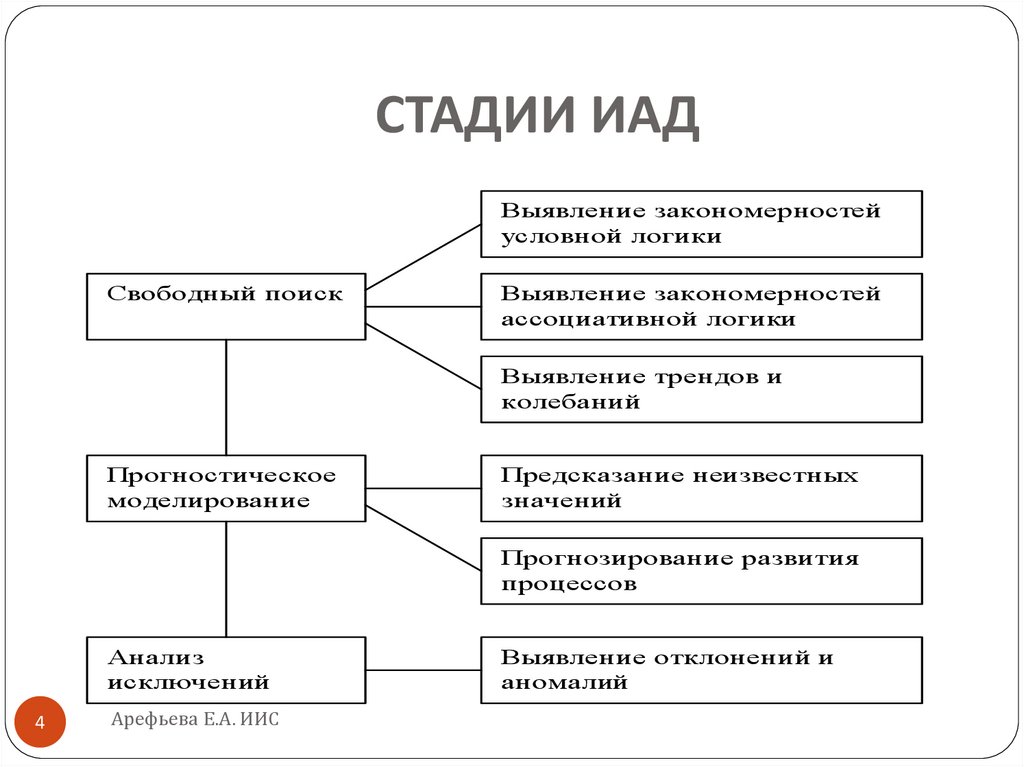
СТАДИИ ИАДВыявление закономерностей
условной логики
Свободный поиск
Выявление закономерностей
ассоциативной логики
Выявление трендов и
колебаний
Прогностическое
моделирование
Предсказание неизвестных
значений
Прогнозирование развития
процессов
Анализ
исключений
4
Арефьева Е.А. ИИС
Выявление отклонений и
аномалий
5.
ДСМ - методДжон Стюарт Милль предложил принципы
индуктивного вывода, которые положены в
основу метода автоматического порождения
гипотез. Способы установления причинноследственных отношений, предложенные
Миллем, основываются на идеях выявления
сходства и различия в наблюдаемых ситуациях.
Схемы Миля справедливы лишь при условии,
что в описании ситуации присутствует полное
множество наблюдаемых фактов и явлений.
5
Арефьева Е.А. ИИС
6.
Принципы индукции1. Принцип
единственного различия:
«Если после введения
какого-либо фактора
появляется (или после
его удаления исчезает)
известное явление,
причем мы не вводим и
не удаляем никакого
другого обстоятельства,
которое могло бы иметь
влияние, то указанный
фактор составляет
причину явления».
6
Арефьева Е.А. ИИС
A, B, C D
B, C
D
A D
7.
Принципы индукции2. Принцип
единственного
совпадения: «Если
все обстоятельства
явления, кроме
одного, могут
отсутствовать, не
уничтожая этим
явления, то это
обстоятельство
является причиной
данного явления»
7
Арефьева Е.А. ИИС
A, B, C D
A, C D
A, B D
A D
8.
Принципы индукции3. Принцип
единственного
остатка: «Если
вычесть из какоголибо явления ту его
часть, которая
является следствием
известных причин, то
остаток явления есть
следствие остальных
причин»
8
Арефьева Е.А. ИИС
A, B, C D, E
B, C E
A D
9.
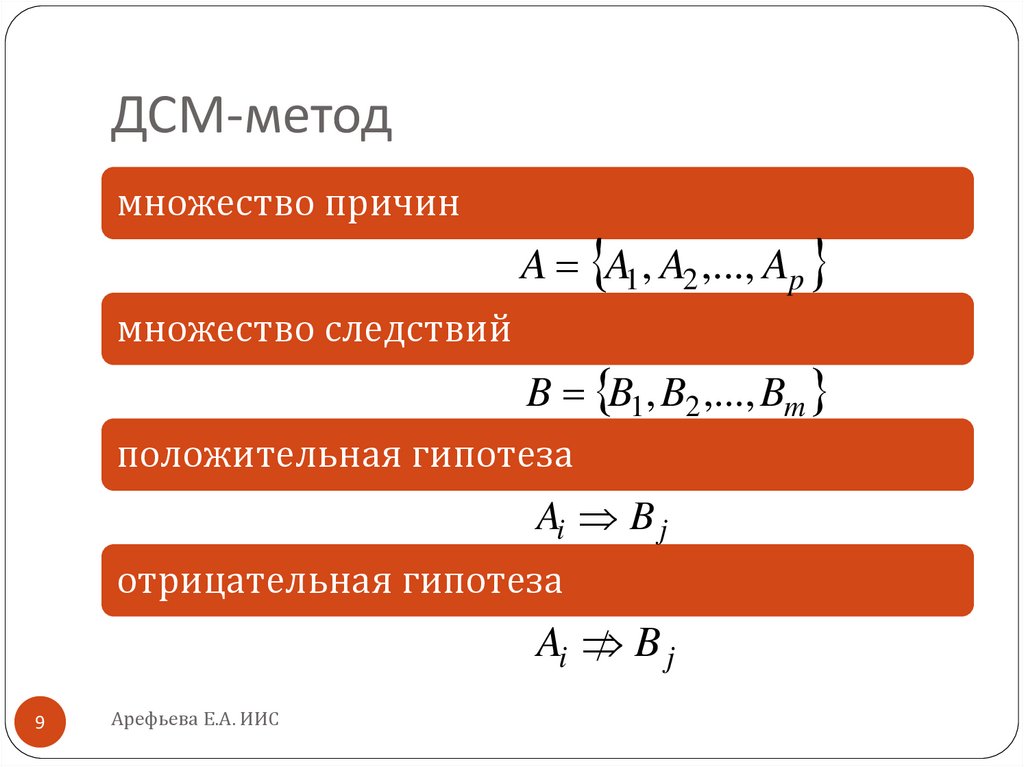
ДСМ-методмножество причин
A A1 , A2 ,..., Ap
множество следствий
B B1, B2 ,..., Bm
положительная гипотеза
Ai B j
отрицательная гипотеза
Ai
Bj
9
Арефьева Е.А. ИИС
10.
ДСМ-методПоложительные и
отрицательные гипотезы:
B1 ... Bm
A1
M
...
Ap
h11
... h1 m
... ... ...
h p 1 ... h pm
A1
M
...
Ap
B1
h11
...
h p 1
10
Арефьева Е.А. ИИС
... Bm
... h1 m
... ...
... h pm
если некоторая гипотеза
имела оценку k n
(число определенных
ранее положительных
гипотез к общему числу
примеров
соответственно), оценки
гипотез изменяются
следующим образом:
k 1 n 1
иначе
k 1 n 1
hij
11.
Байесовская классификацияНаивно-байесовский подход (naive-bayes approach)
является наиболее простым вариантом метода,
использующего байесовские сети.
"Наивная" классификация - достаточно прозрачный
и понятный метод классификации, исходит из
предположения о взаимной независимости
признаков.
Свойства наивной классификации:
- Использование всех переменных и определение всех
зависимостей между ними.
- Наличие двух предположений относительно
переменных: все переменные являются одинаково
важными; все переменные являются статистически
независимыми, т.е. значение одной переменной
ничего не говорит о значении другой.
11
Арефьева Е.А. ИИС
12.
Байесовская классификацияБайесовский подход предполагает начальное априорное задание
предполагаемых гипотез, которые последовательно уточняются с учетом
вероятностей свидетельств в пользу или против гипотез, в результате
чего формируются апостериорные вероятности:
P H E P E H *
P H
P E
P H E P E H *
где P H - априорная вероятность гипотезы Н;
P H 1 - P H
P E
P H
P E
- априорная вероятность отрицания гипотезы Н;
- априорная вероятность свидетельства Е;
P H E - апостериорная (условная) вероятность гипотезы Н при условии, что
имеет место свидетельство Е;
P H E - апостериорная (условная) вероятность отрицания гипотезы Н при
условии, что имеет место свидетельство Е;
P E H - вероятность свидетельства гипотезы Е при подтверждении Н;
P E H - вероятность свидетельства гипотезы Е при отрицании гипотезы Н.
12
Арефьева Е.А. ИИС
13.
Байесовская классификацияНайдем отношения
левых и правых частей
представленных
Р( Н / Е )
P( E / H ) P( H )
*
или
Р(^ H / E ) P( E /^ H ) P(^ H )
O ( H / E ) Ls * O ( H )
уравнений:
Где O( H )- априорные шансы гипотезы Н, отражающие
отношение числа позитивных проявлений гипотезы к числу
негативных;
O( H E-) апостериорные шансы гипотезы Н при условии
наличия свидетельства Е;
Ls- фактор достаточности, отражающий степень воздействия
на шансы гипотезы при наличии свидетельства Е.
Аналогично выводится зависимость: O( H / E ) Ln * O( H )
где O( H E-)апостериорные шансы гипотезы Н при условии
отсутствия свидетельства Е;
Ln- фактор необходимости, отражающий степень
воздействия на шансы гипотезы при отсутствии
свидетельства Е.
13
Арефьева Е.А. ИИС
14.
Достоинства байесовских сетей какметода Data Mining
в модели определяются зависимости между всеми
переменными, это позволяет легко обрабатывать ситуации, в
которых значения некоторых переменных неизвестны;
байесовские сети достаточно просто интерпретируются и
позволяют на этапе прогностического моделирования легко
проводить анализ по сценарию "что, если";
байесовский метод позволяет естественным образом
совмещать закономерности, выведенные из данных, и,
например, экспертные знания, полученные в явном виде;
использование байесовских сетей позволяет избежать
проблемы переучивания (overfitting), то есть избыточного
усложнения модели, что является слабой стороной многих
методов (например, деревьев решений и нейронных сетей).
14
Арефьева Е.А. ИИС
15.
Деревья решенийДеревья решений – метод структурирования задачи в виде
древовидного графа, вершины которого соответствуют
продукционным правилам, позволяющим классифицировать
данные или осуществлять анализ последствий решений.
Области применения деревьев решений:
Описание данных. Деревья решений позволяют хранить
информацию о данных в компактной форме, вместо них
можно хранить дерево решений, которое содержит точное
описание объектов.
Классификация. Отнесение объектов к одному из ранее
известных классов.
Регрессия. Если целевая переменная имеет непрерывные
значения, деревья решений позволяют установить
зависимость целевой переменной от независимых.
15
Арефьева Е.А. ИИС
16.
Алгоритм ID31. Выбирается случайным образом
некоторое подмножество (окно) из
множества обучающих примеров.
2. Для текущего окна строятся правила
классификации.
3. Просматривается обучающая выборка на
предмет нахождения исключений из
построенных правил классификации.
4. Если исключения найдены, то они
добавляются в окно и возвращаемся на
шаг 2.
5. Для построенной классификации строим
продукционные правила.
16
Арефьева Е.А. ИИС
Правила классификации
строятся, циклически
просматривая и разбивая
обучающие примеры на
группы в соответствии с
переменной, имеющей
наибольшую
классифицирующую силу.
Каждое подмножество,
выделяемое такой
переменной, вновь
разбивается на группы с
использованием
следующей переменной с
наибольшей
классифицирующей
способностью и т.д.
Процедура разбиения
заканчивается, когда в
группе остаются примеры
одного класса. В ходе
этого процесса строится
дерево классификации.
17.
Построение деревьев классификацииВ качестве значения классифицирующей силы
переменной используется энтропия:
ni
ni
E
logk
ni
ni
i 1
i
i
k
где k – количество групп,
ni – количество примеров
в i-ой группе.
17
Арефьева Е.А. ИИС
18.
Метод InduceОсновная идея алгоритма – найти такие
классифицирующие правила, которые просты и
охватывают множество примеров, отбросить
сложные и охватывающие лишь несколько
случаев.
Существенным для метода фактором является
процедура обобщений.
Предположим, мы получили
классификационное правило:
A Az B Bz C C z
18
Арефьева Е.А. ИИС
19.
A Az B Bz C C zЗаменить конъюнкции на
дизъюнкцию:
A Az B Bz C Cz
A Az B Bz C Cz
A Az B Bz C Cz
19
Арефьева Е.А. ИИС
20.
A Az B Bz C C zОтбросить часть условия:
A Az B Bz
A Az C Cz
B Bz C Cz
20
Арефьева Е.А. ИИС
21.
A Az B Bz C C zРасширить область
действия факта условия:
A Az B Bz C Cz
A Az B Bz C Cz
A Az B Bz C Cz
21
Арефьева Е.А. ИИС
Az Az
22.
Метод опорных векторовМетод опорных векторов относится к группе
граничных методов. Она определяет классы при
помощи границ областей.
При помощи данного метода решаются задачи
бинарной классификации.
Цель метода опорных векторов - найти плоскость,
разделяющую два множества объектов.
Метод опорных векторов позволяет:
получить функцию классификации с минимальной
верхней оценкой ожидаемого риска (уровня
ошибки классификации);
использовать линейный классификатор для работы
с нелинейно разделяемыми данными, сочетая
простоту с эффективностью.
22
Арефьева Е.А. ИИС
23.
Алгоритм распознавания типа«Кора»
Алгоритм относится к группе тестовых алгоритмов.
Исходные данные представляются в двоичном виде в виде матрицы,
столбцами которой являются классифицирующие переменные, строки
– обучающие примеры.
Тест матрицы называется совокупность таких столбцов, что после
удаления остальных все пары строк, принадлежащих разным классам
различны. Тест называется тупиковым, если никакая его часть не
является тестом.
Набор столбцов матрицы называются покрытием, если каждая строка
матрицы в пересечении хотя бы с одним столбцом дает 1. Покрытие
неприводимо, если никакое его собственное подмножество не является
покрытием.
В случае бинарной информации задача построения множества всех
неприводимых покрытий, порождаемых объектами одного класса,
сводится к построению булевой функции, объединяющей
дизъюнктивно все неприводимые покрытия, внутри соединенные
конъюнкцией. Значения этой функции равно 1 на наборах,
описывающих объекты выделенного класса и 0 – на остальных.
23
Арефьева Е.А. ИИС
24.
Системы рассуждений на основеаналогичных случаев
Прецедент - это описание ситуации в сочетании с подробным
указанием действий, предпринимаемых в данной ситуации.
Подход, основанный на прецедентах, условно можно поделить на
следующие этапы:
сбор подробной информации о поставленной задаче;
сопоставление этой информации с деталями прецедентов,
хранящихся в базе, для выявления аналогичных случаев;
выбор прецедента, наиболее близкого к текущей проблеме, из базы
прецедентов;
адаптация выбранного решения к текущей проблеме, если это
необходимо;
проверка корректности каждого вновь полученного решения;
занесение детальной информации о новом прецеденте в базу
прецедентов.
24
Арефьева Е.А. ИИС
25.
Методы кластерного анализаКластерный анализ позволяет сокращать размерность
данных, делать ее наглядной. Кластерный анализ может
применяться к совокупностям временных рядов, здесь
могут выделяться периоды схожести некоторых
показателей и определяться группы временных рядов со
схожей динамикой.
Задачи кластерного анализа :
Разработка типологии или классификации.
Исследование полезных концептуальных схем
группирования объектов.
Представление гипотез на основе исследования данных.
Проверка гипотез или исследований для определения,
действительно ли типы (группы), выделенные тем или
иным способом, присутствуют в имеющихся данных.
25
Арефьева Е.А. ИИС
26.
Иерархическая кластеризация26
Арефьева Е.А. ИИС
27.
Партициальная кластеризацияКластеризация состоит в разделении набора данных на
определенное количество отдельных кластеров.
Существует два подхода. Первый заключается в
определении границ кластеров как наиболее плотных
участков в многомерном пространстве исходных данных,
т.е. определение кластера там, где имеется большое
"сгущение точек". Второй подход заключается в
минимизации меры различия объектов
Алгоритм k-средних строит k кластеров, расположенных на
возможно больших расстояниях друг от друга. Основной
тип задач, которые решает алгоритм k-средних, - наличие
предположений (гипотез) относительно числа кластеров,
при этом они должны быть различны настолько, насколько
это возможно. Выбор числа k может базироваться на
результатах предшествующих исследований,
теоретических соображениях или интуиции.
27
Арефьева Е.А. ИИС
28.
Алгоритм k-среднихОбщая идея
алгоритма:
заданное
фиксированное
число k
кластеров
наблюдения
сопоставляются
кластерам так,
что средние в
кластере (для
всех
переменных)
максимально
возможно
отличаются
друг от друга.
28
Арефьева Е.А. ИИС
29.
Спасибо за внимание!!!29
Арефьева Е.А. ИИС



























 informatics
informatics








