Similar presentations:
Колебания. Лекция 3
1.
Колебания – движения или процессы, характеризующиеся определеннойповторяемостью во времени
Периодические колебания – величины, описывающие
процессы повторяются через равные промежутки времени
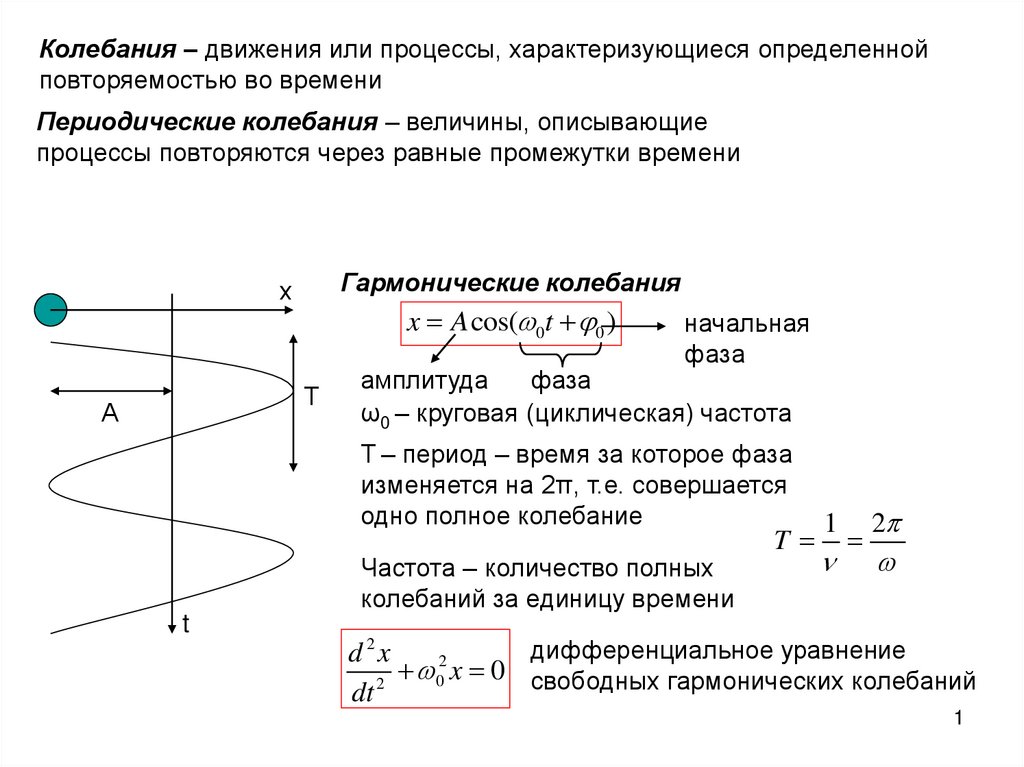
Гармонические колебания
х
x A cos( 0t 0 )
Т
А
начальная
фаза
амплитуда
фаза
ω0 – круговая (циклическая) частота
Т – период – время за которое фаза
изменяется на 2π, т.е. совершается
одно полное колебание
Частота – количество полных
колебаний за единицу времени
t
T
1
2
дифференциальное уравнение
d 2x
2
0 x 0 свободных гармонических колебаний
2
dt
1
2.
x A cos( 0t 0 )Зависимость координаты от времени
dx
v
0 A sin( 0t 0 )
Зависимость скорости от времени
dt
dv
a
02 A cos( 0t 0 ) 02 x Зависимость ускорения от времени
dt
F ma m 02 x
Сила, действующая на тело
Кинетическая энергия
Потенциальная энергия
mv 2 mA2 02
Ek
sin 2 ( 0t 0 )
2
2
mA2 02
En Fdx
cos 2 ( 0t 0 )
2
Полная механическая энергия
mA2 02
E Ek En
2
2
3.
дифференциальное уравнениеd 2x
2
x
0
0
свободных гармонических колебаний
dt 2
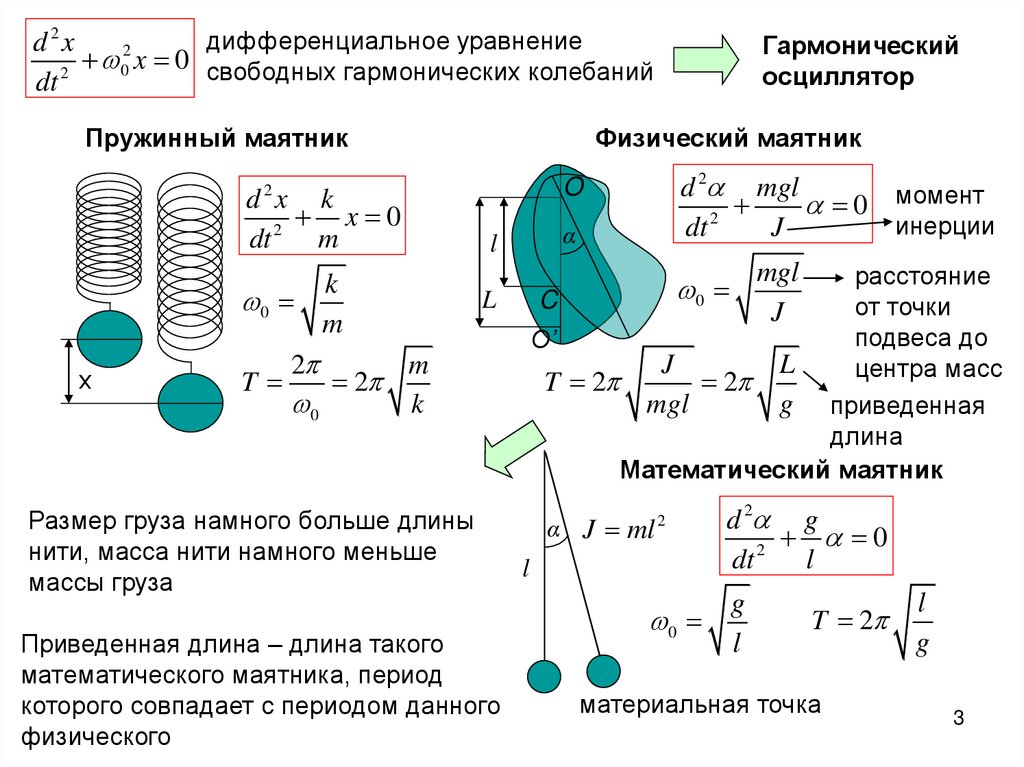
Пружинный маятник
Физический маятник
х
k
0
m
2
m
T
2
0
k
d 2 mgl
момент
0
инерции
dt 2
J
O
2
d x k
x 0
2
dt
m
Гармонический
осциллятор
α
l
расстояние
C
от точки
подвеса до
O’
J
L
центра масс
T 2
2
mgl
g приведенная
длина
Математический маятник
L
Размер груза намного больше длины
нити, масса нити намного меньше
массы груза
Приведенная длина – длина такого
математического маятника, период
которого совпадает с периодом данного
физического
mgl
J
0
α J ml
2
l
0
d 2 g
0
2
dt
l
g
l
T 2
материальная точка
l
g
3
4.
дифференциальное уравнениеd 2x
2
x
0
0
свободных гармонических колебаний
dt 2
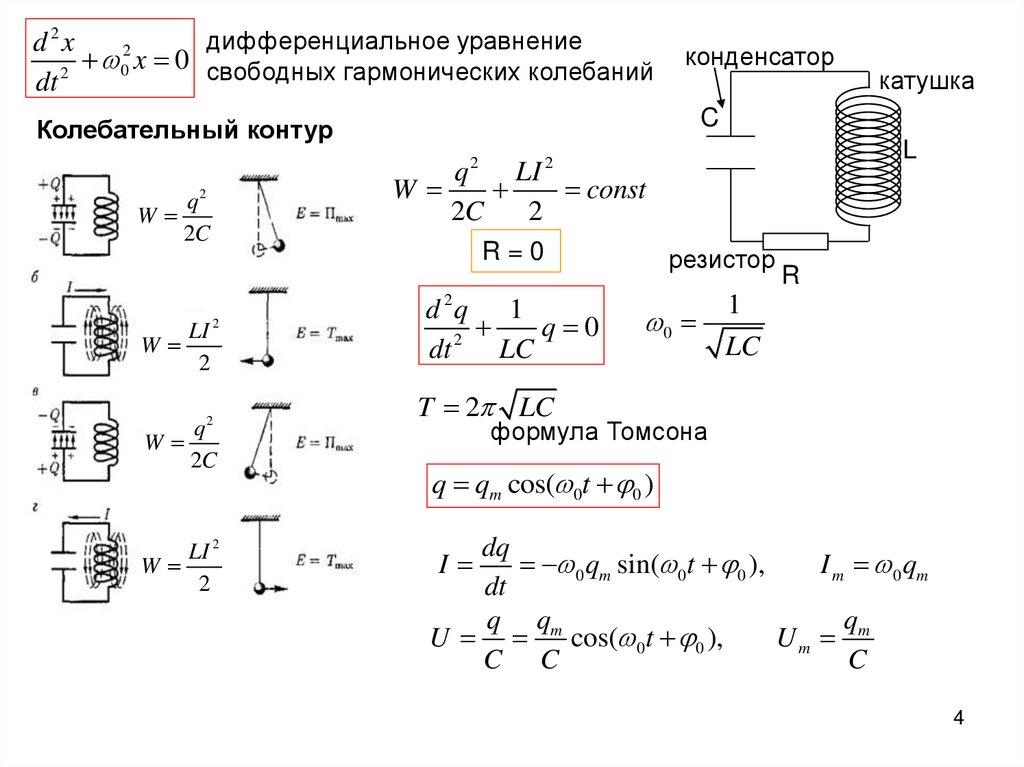
конденсатор
Колебательный контур
C
W
LI
2
L
q 2 LI 2
W
const
2C
2
q2
W
2C
R=0
2
q2
W
2C
LI 2
W
2
d 2q 1
q 0
dt 2 LC
катушка
резистор
0
R
1
LC
T 2 LC
формула Томсона
q qm cos( 0t 0 )
dq
0 qm sin( 0t 0 ),
I m 0 qm
dt
q
q q
U m cos( 0t 0 ),
Um m
C C
C
I
4
5.
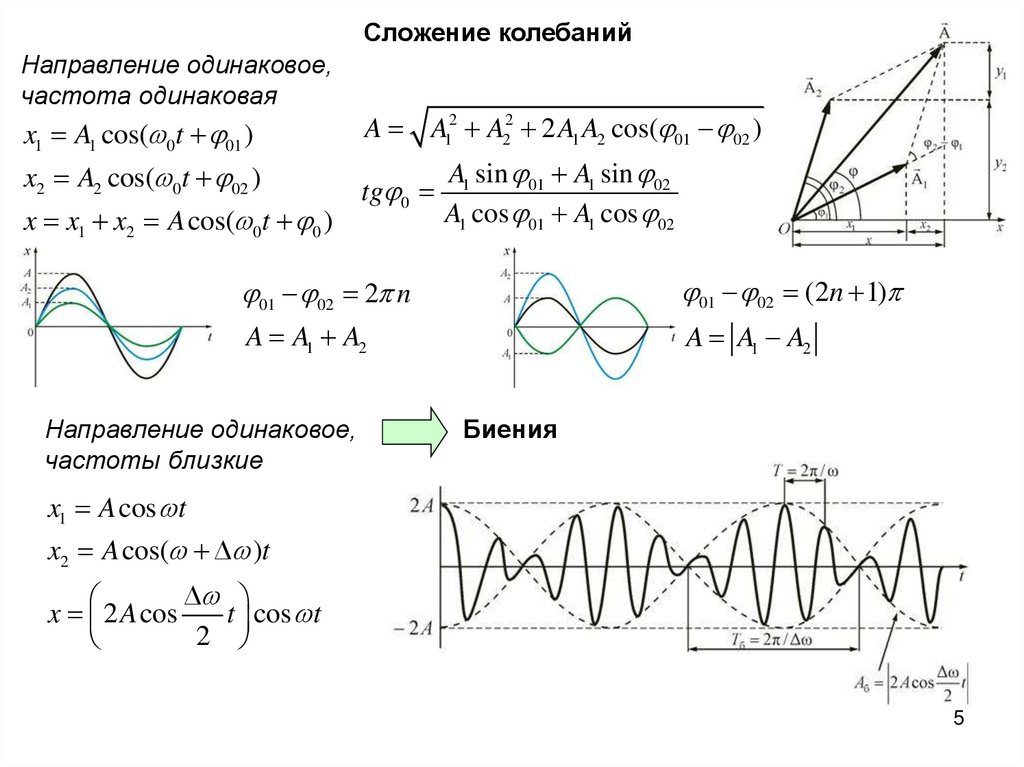
Сложение колебанийНаправление одинаковое,
частота одинаковая
x1 A1 cos( 0t 01 )
A A12 A22 2 A1 A2 cos( 01 02 )
x2 A2 cos( 0t 02 )
tg 0
x x1 x2 A cos( 0t 0 )
A1 sin 01 A1 sin 02
A1 cos 01 A1 cos 02
01 02 2 n
01 02 (2n 1)
A A1 A2
A A1 A2
Направление одинаковое,
частоты близкие
Биения
x1 A cos t
x2 A cos( )t
x 2 A cos
t cos t
2
5
6.
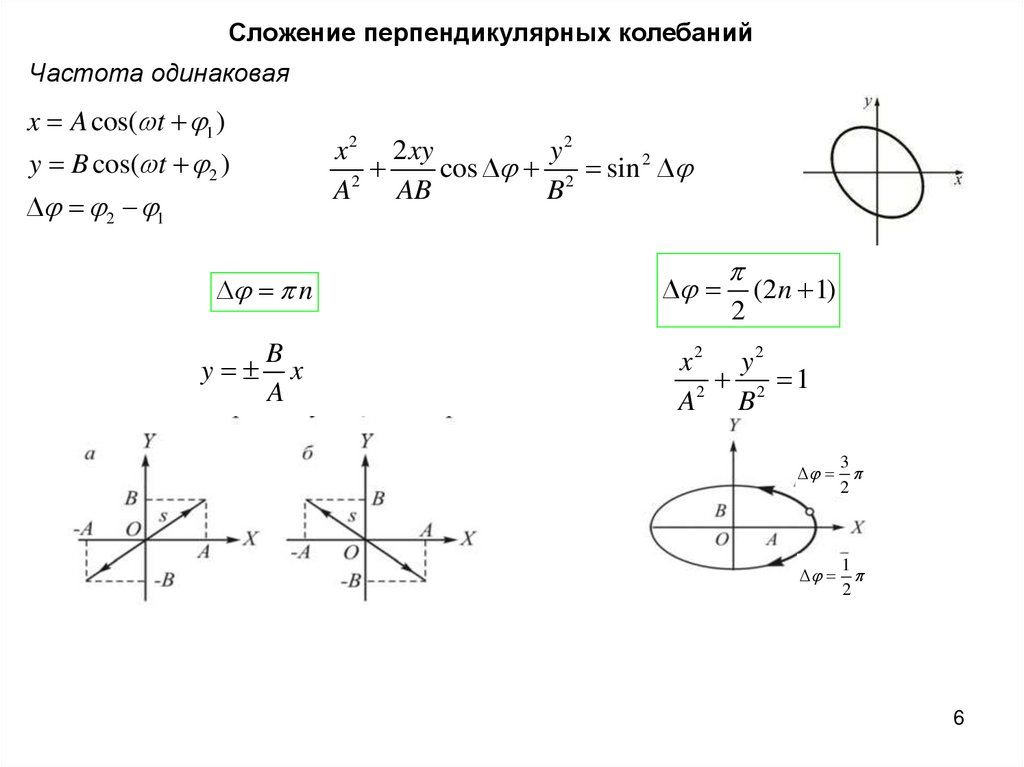
Сложение перпендикулярных колебанийЧастота одинаковая
x A cos( t 1 )
y B cos( t 2 )
2 1
x 2 2 xy
y2
cos 2 sin 2
2
A
AB
B
n
B
y x
A
x2 y 2
2 1
2
A B
2
(2n 1)
3
2
1
2
6
7.
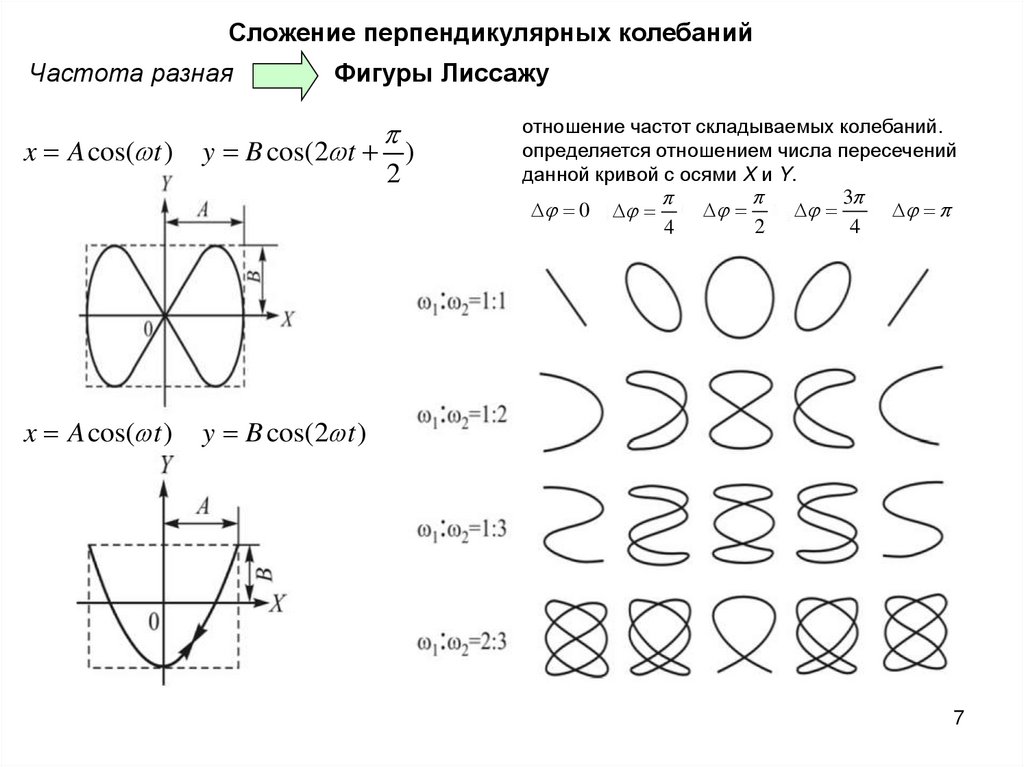
Сложение перпендикулярных колебанийЧастота разная
Фигуры Лиссажу
x A cos( t )
y B cos(2 t )
2
x A cos( t )
y B cos(2 t )
отношение частот складываемых колебаний.
определяется отношением числа пересечений
данной кривой с осями X и Y.
3
0
4
2
4
7
8.
Затухающие колебания - колебания, амплитуды которых из-за потерьэнергии реальной колебательной системой с течением времени уменьшаются
дифференциальное уравнение
d 2x
dx
2
2
x
0
0
свободных затухающих колебаний
dt 2
dt
ω0 – циклическая частота свободных (незатухающих)
колебаний данной системы – собственная частота
коэффициент затухания
x A0 e t cos( t )
2 02 2
A A0e t - амплитуда затухающих колебаний
1 Время релаксации - промежуток времени за которое
амплитуда затухающих колебаний уменьшается в е раз.
T
2
2
02 2
A(t)
T
1
ln
T
A(t T)
Ne
Q
Логарифмический
декремент затухания
Добротность
Ne
0
2
Если затухание мало, то
можно условно пользоваться
понятием периода как
промежутка времени между
двумя последующими
максимумами
Ne – число колебаний,
совершаемых системой
за время релаксации
8
9.
d 2xdx
2
02 x 0
2
dt
dt
дифференциальное уравнение
свободных затухающих колебаний
Пружинный маятник
Затухания под действием силы трения F r v, r – коэффициент сопротивления
0
k
r
1
,
, Q
km
m
2m
r
Колебательный контур
d 2 q R dq 1
q 0
2
dt
L dt LC
R≠0
0
1
R
1 L
,
, Q
2
L
R C
LC
При увеличении коэффициента затухания период затухающих
колебаний растет при 0
обращается в бесконечность, т.е.
движение перестает быть периодическим
9
10.
Вынужденные механическиеколебания
возникают под действием внешней
периодически изменяющейся силы
Вынужденные электромагнитные
колебания
Возникают под действием внешней
периодически изменяющейся ЭДС
F F0 cos t
U U m cos t
F0
d 2x
dx
2
2
x
cos t
0
2
dt
dt
m
Um
d 2 q R dq 1
q
cos t
2
dt
L dt LC
L
d 2s
ds
2
2
s x0 cos t
0
2
dt
dt
s A cos( t )
x0
A
( 02 2 ) 2 4 2 2
tg
2
02 2
10
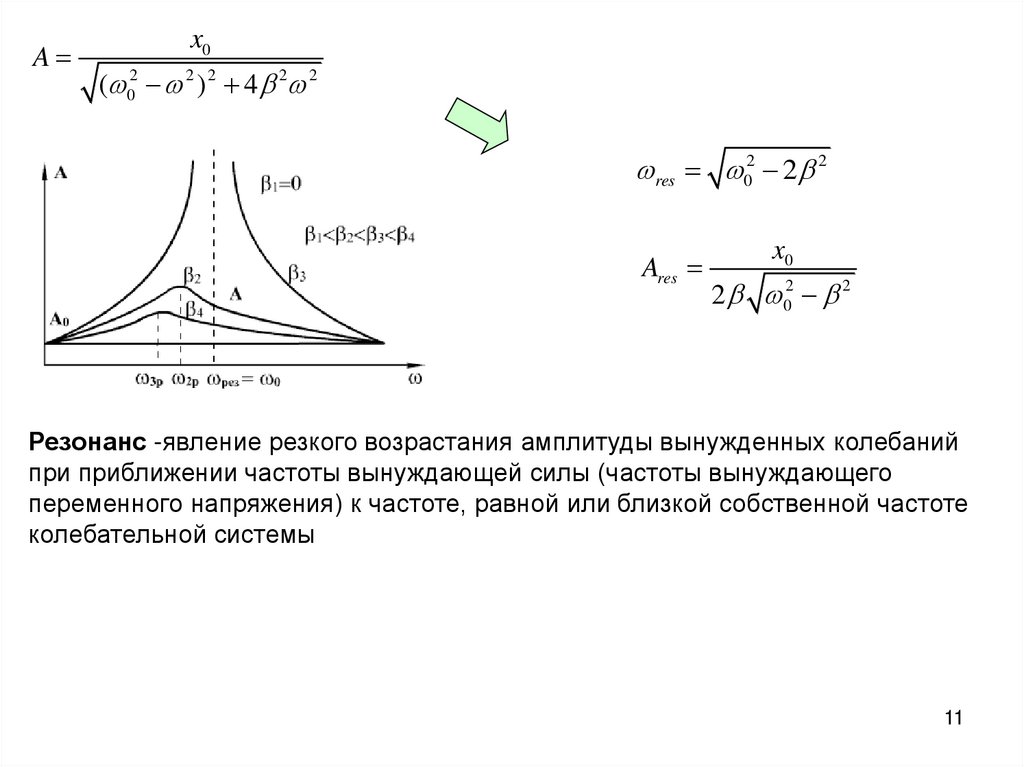
11.
Ax0
( 02 2 ) 2 4 2 2
res 02 2 2
Ares
x0
2 02 2
Резонанс -явление резкого возрастания амплитуды вынужденных колебаний
при приближении частоты вынуждающей силы (частоты вынуждающего
переменного напряжения) к частоте, равной или близкой собственной частоте
колебательной системы
11
12.
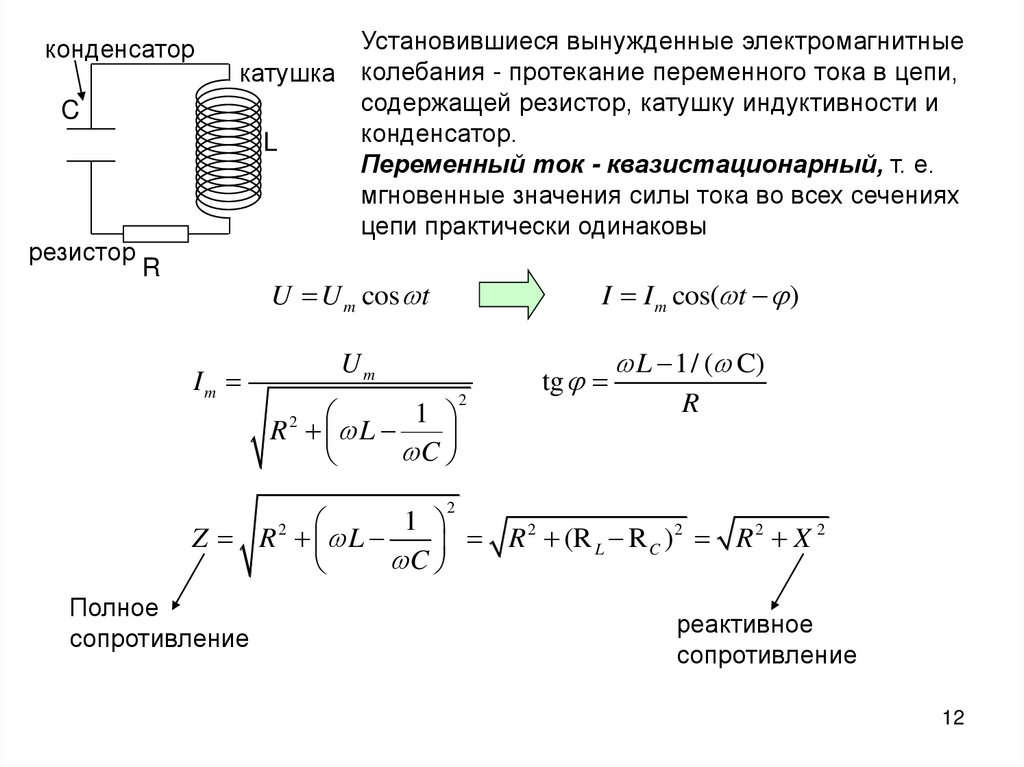
конденсаторC
резистор
Установившиеся вынужденные электромагнитные
катушка колебания - протекание переменного тока в цепи,
содержащей резистор, катушку индуктивности и
конденсатор.
L
Переменный ток - квазистационарный, т. е.
мгновенные значения силы тока во всех сечениях
цепи практически одинаковы
R
I I m cos( t )
U U m cos t
Im
Um
1
R2 L
C
2
tg
L 1/ ( C)
R
2
1
2
2
2
2
Z R L
R
(R
R
)
R
X
L
C
C
2
Полное
сопротивление
реактивное
сопротивление
12
13.
Волна – процесс распространения колебанийОсновное свойство всех волн - перенос энергии без переноса вещества.
Упругие (механические) волны - механические возмущения,
распространяющиеся в упругой среде
Продольные волны – частицы среды совершают
колебания в направлении распространения волны,
Деформация сжатия и
растяжения
Твердые, жидкие и
газообразные среды
Поперечные волны - частицы среды совершают
колебания в плоскостях, перпендикулярных
направлению распространения волны
Деформация сдвига
Твердые среды
13
14.
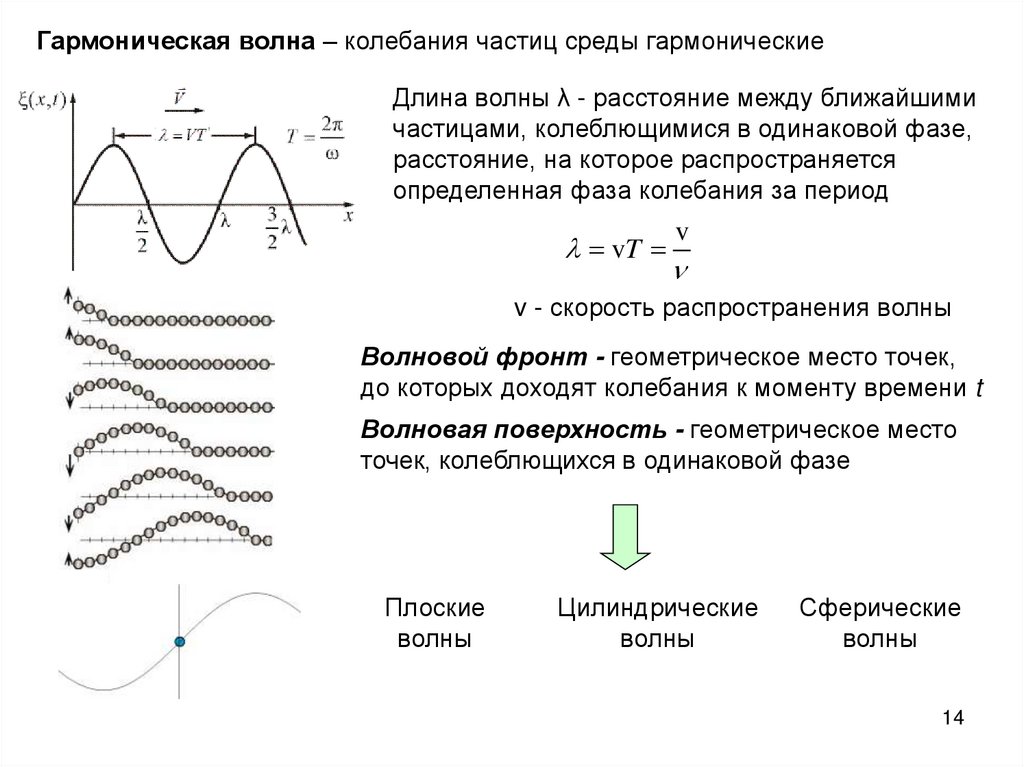
Гармоническая волна – колебания частиц среды гармоническиеДлина волны λ - расстояние между ближайшими
частицами, колеблющимися в одинаковой фазе,
расстояние, на которое распространяется
определенная фаза колебания за период
vT
v
v - скорость распространения волны
Волновой фронт - геометрическое место точек,
до которых доходят колебания к моменту времени t
Волновая поверхность - геометрическое место
точек, колеблющихся в одинаковой фазе
Плоские
волны
Цилиндрические
волны
Сферические
волны
14
15.
Бегущие волны - волны, которые переносят в пространстве энергиюУравнение плоской волны
s( x, t ) A cos( t kx 0 )
амплитуда
фаза
начальная
фаза
k
2
v
ω – циклическая частота
k – волновое число
Уравнение сферической волны (справедливо для точечных источников)
s (r , t )
A
cos( t kr 0 ) r - расстояние от центра волны до
r
рассматриваемой точки среды
Волновое уравнение для однородной изотропной среды
1 2s
s 2 2
v t
2
2
2
2 2 2
x y z
оператор Лапласа
2 s 1 2 s Волновое уравнение для плоской волны,
2 2
2
x
v t распространяющейся вдоль оси х
15
16.
Принцип суперпозиции (наложения) волн:при распространении в линейной среде нескольких волн каждая из них
распространяется так, как будто другие волны отсутствуют, а результирующее
смещение частицы среды в любой момент времени равно геометрической
сумме смещений, которые получают частицы, участвуя в каждом из слагающих
волновых процессов
Волновой пакет - суперпозиция волн, мало
отличающихся друг от друга по частоте, занимающая в
каждый момент времени ограниченную область
пространства
Групповая скорость и - скорость движения
группы волн, образующих в каждый момент
времени локализованный в пространстве
волновой пакет
u v-
Фазовая скорость v - скорость
перемещения фазы волны
dv
d
Если фазовая скорость волн в среде зависит от их частоты (длины волны), то
это явление называют дисперсией волн
16
17.
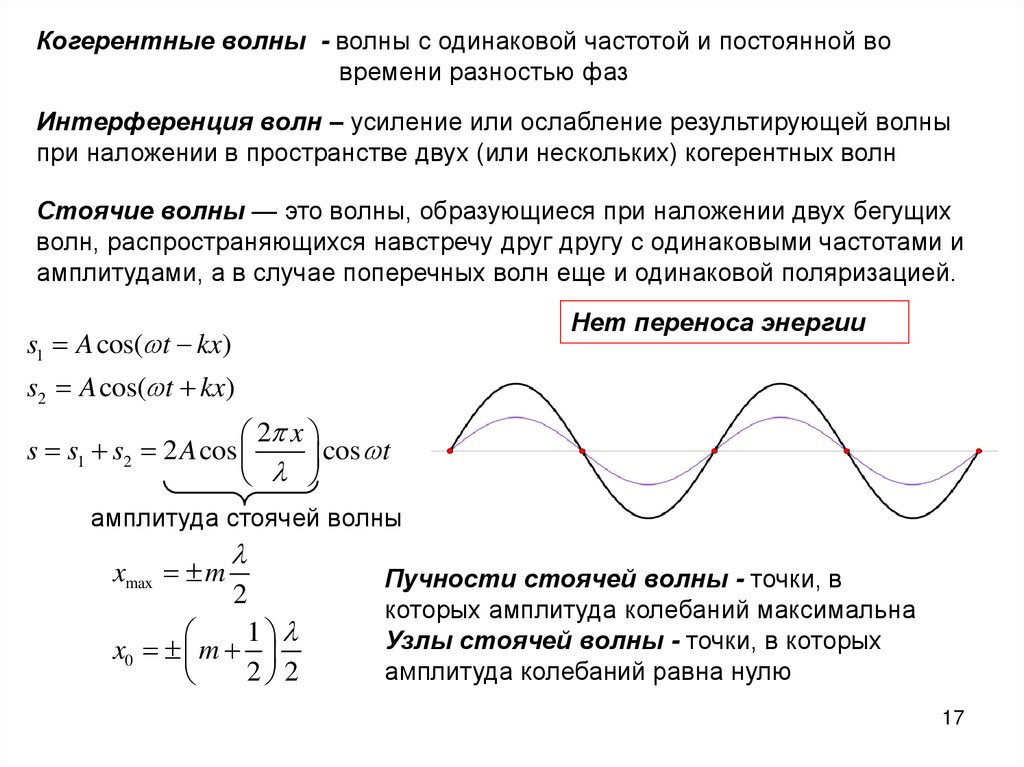
Когерентные волны - волны с одинаковой частотой и постоянной вовремени разностью фаз
Интерференция волн – усиление или ослабление результирующей волны
при наложении в пространстве двух (или нескольких) когерентных волн
Стоячие волны — это волны, образующиеся при наложении двух бегущих
волн, распространяющихся навстречу друг другу с одинаковыми частотами и
амплитудами, а в случае поперечных волн еще и одинаковой поляризацией.
Нет переноса энергии
s1 A cos( t kx)
s2 A cos( t kx)
2 x
s s1 s2 2 A cos
cos t
амплитуда стоячей волны
xmax m
2
1
x0 m
2 2
Пучности стоячей волны - точки, в
которых амплитуда колебаний максимальна
Узлы стоячей волны - точки, в которых
амплитуда колебаний равна нулю
17
18.
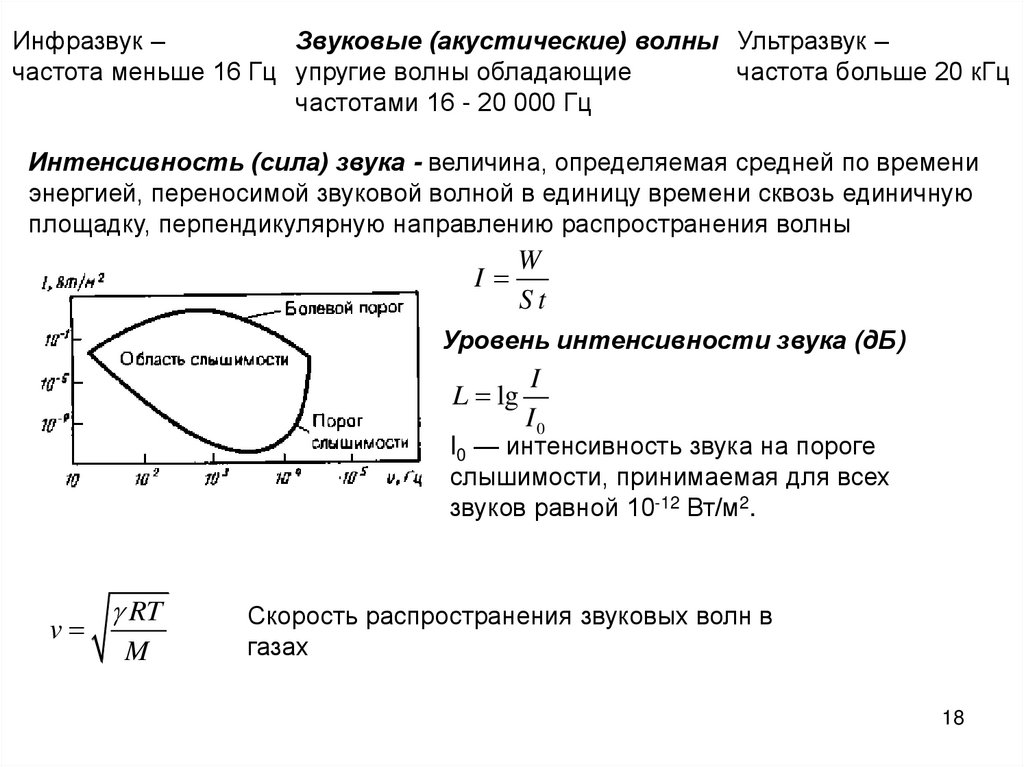
Инфразвук –Звуковые (акустические) волны Ультразвук –
частота меньше 16 Гц упругие волны обладающие
частота больше 20 кГц
частотами 16 - 20 000 Гц
Интенсивность (сила) звука - величина, определяемая средней по времени
энергией, переносимой звуковой волной в единицу времени сквозь единичную
площадку, перпендикулярную направлению распространения волны
I
W
St
Уровень интенсивности звука (дБ)
L lg
I
I0
I0 — интенсивность звука на пороге
слышимости, принимаемая для всех
звуков равной 10-12 Вт/м2.
v
RT
M
Скорость распространения звуковых волн в
газах
18
19.
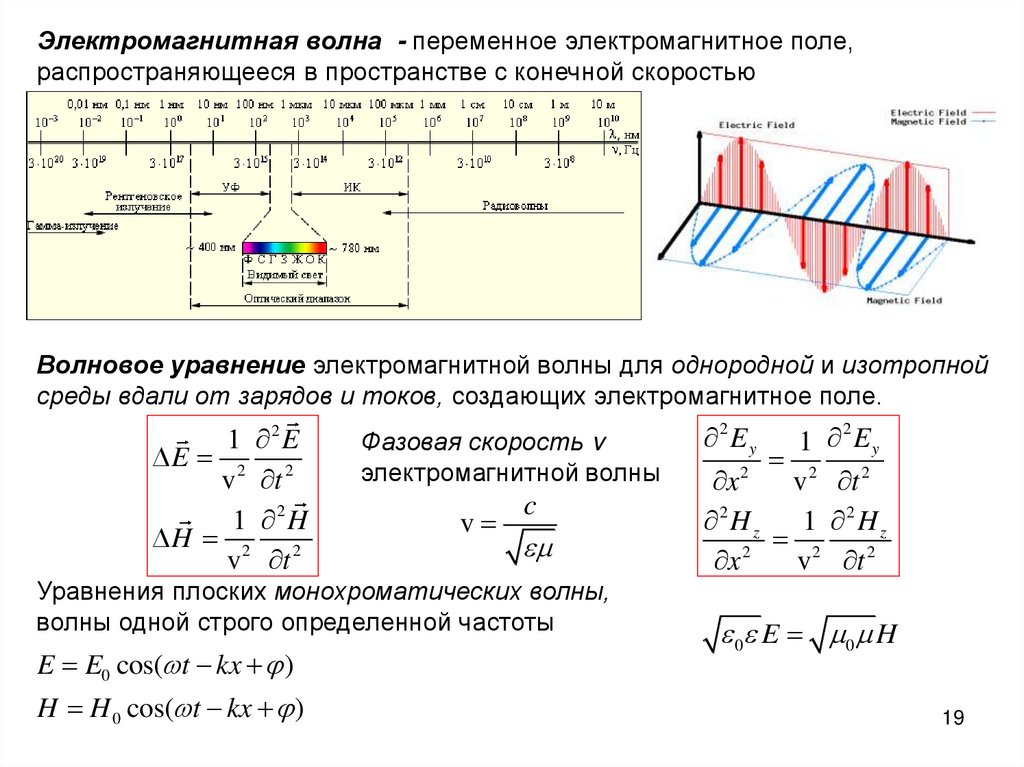
Электромагнитная волна - переменное электромагнитное поле,распространяющееся в пространстве с конечной скоростью
Волновое уравнение электромагнитной волны для однородной и изотропной
среды вдали от зарядов и токов, создающих электромагнитное поле.
1 2 E
E 2 2
v t
1 2 H
H 2 2
v t
Фазовая скорость v
электромагнитной волны
v
c
Уравнения плоских монохроматических волны,
волны одной строго определенной частоты
E E0 cos( t kx )
H H 0 cos( t kx )
2 Ey
1 Ey
2
2
x
v t 2
2 H z 1 2 H z
2
2
x
v t 2
2
0 E 0 H
19
20.
Объемная плотность энергии электромагнитной волныw wel wm
0 E 2
2
0 H 2
0 E 0 H
2
w 0 0 EH
Вектор плотности потока электромагнитной энергии
(вектор Умова – Пойнтинга)
S E H
Вектор S направлен в сторону распространения электромагнитной волны, его
модуль равен энергии, переносимой электромагнитной волной за единицу
времени через единичную площадку, перпендикулярную направлению
распространения волны.
20
21.
Когерентность - согласованноепротекание во времени и пространстве
нескольких колебательных или
волновых процессов.
Монохроматические волны неограниченные в пространстве
волны одной определенной и строго
постоянной частоты.
Временная когерентность волны
характеризует сохранение взаимной
когерентности при временном
отставании одного из лучей по
отношению к другому
Пространственная
когерентность волны
характеризует наличие
взаимной когерентности двух
световых пучков, взятых из различных
точек сечения волны.
Свет, испускаемый макроскопическим
источником, некогерентен
Интерференция света пространственное перераспределение
светового потока при наложении двух
(или нескольких) когерентных световых
волн происходит, в результате чего в
одних местах возникают максимумы, а в
других - минимумы интенсивности света
21
22.
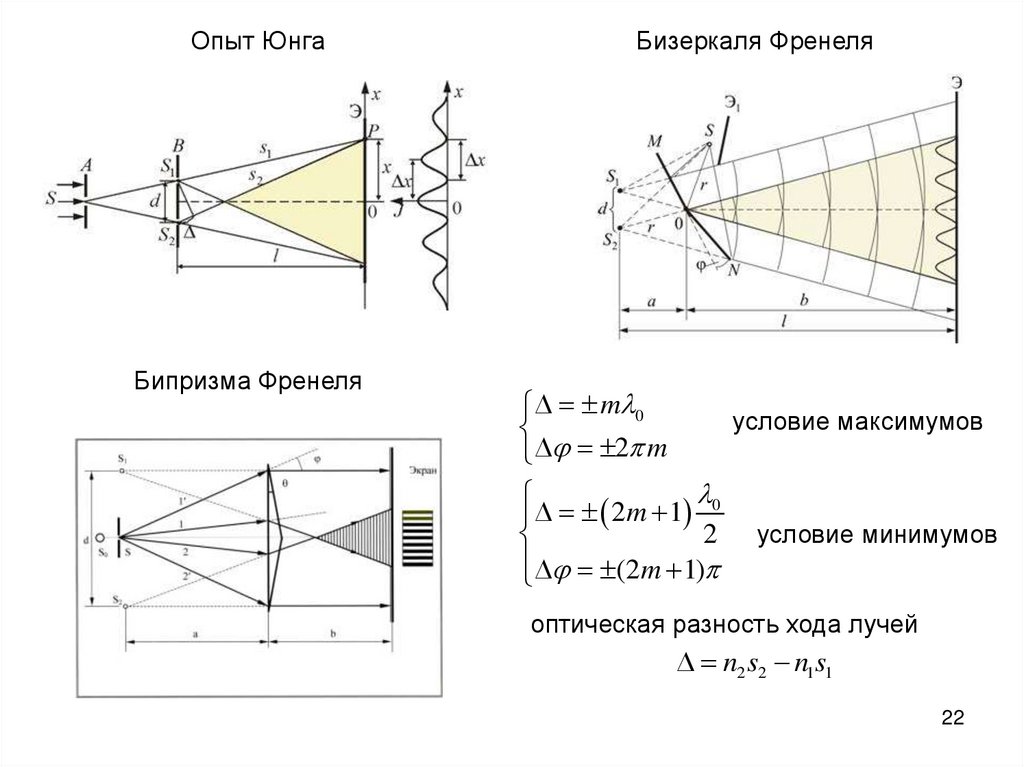
Опыт ЮнгаБипризма Френеля
Бизеркаля Френеля
m 0
условие максимумов
2 m
0
2
m
1
2 условие минимумов
(2m 1)
оптическая разность хода лучей
n2 s2 n1s1
22
23.
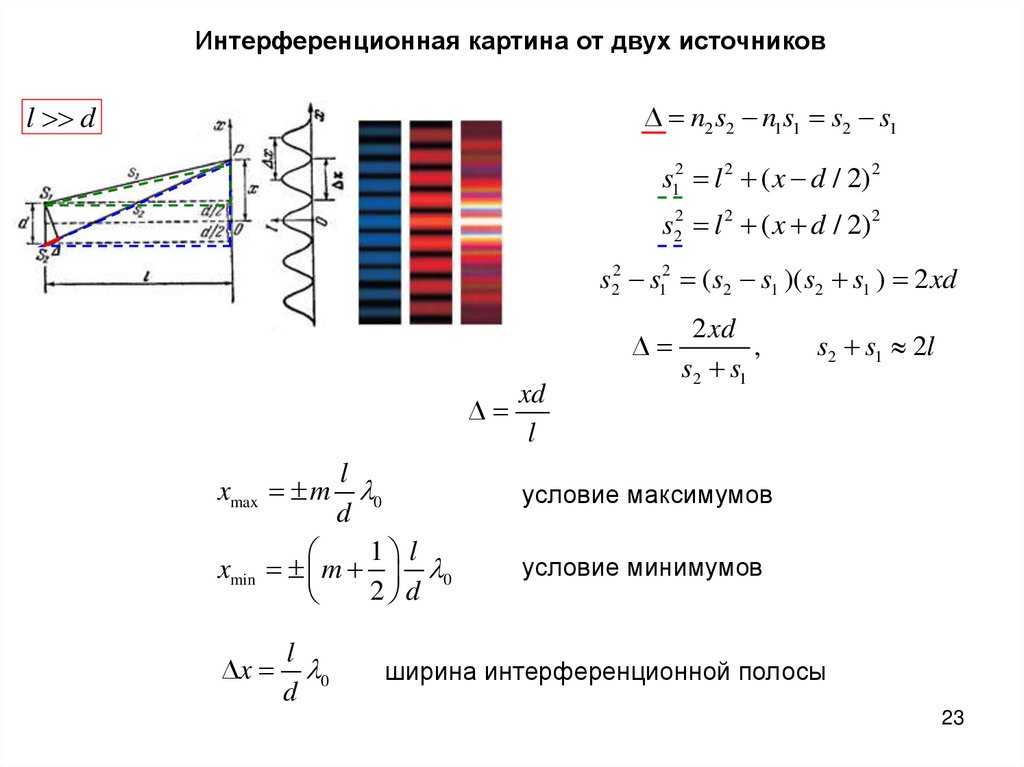
Интерференционная картина от двух источниковl d
n2 s2 n1s1 s2 s1
s12 l 2 ( x d / 2)2
s22 l 2 ( x d / 2)2
s22 s12 ( s2 s1 )( s2 s1 ) 2 xd
l
0
d
1 l
xmin m 0
2 d
xmax m
x
l
0
d
xd
l
2 xd
,
s2 s1
s2 s1 2l
условие максимумов
условие минимумов
ширина интерференционной полосы
23
24.
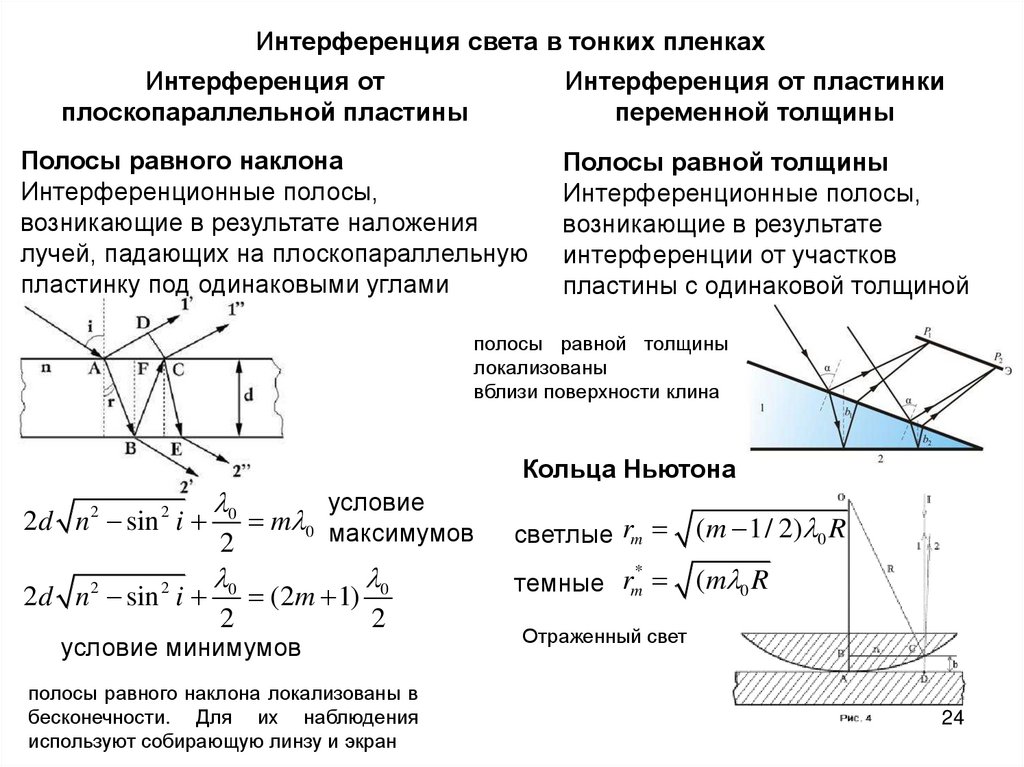
Интерференция света в тонких пленкахИнтерференция от
плоскопараллельной пластины
Интерференция от пластинки
переменной толщины
Полосы равного наклона
Интерференционные полосы,
возникающие в результате наложения
лучей, падающих на плоскопараллельную
пластинку под одинаковыми углами
Полосы равной толщины
Интерференционные полосы,
возникающие в результате
интерференции от участков
пластины с одинаковой толщиной
полосы равной толщины
локализованы
вблизи поверхности клина
Кольца Ньютона
0
условие
2d n sin i m 0 максимумов
2
светлые rm
(m 1/ 2) 0 R
2d n sin i
темные rm
(m 0 R
2
2
2
2
0
2
(2m 1)
условие минимумов
0
2
полосы равного наклона локализованы в
бесконечности. Для их наблюдения
используют собирающую линзу и экран
*
Отраженный свет
24
25.
2526.
2627.
Дифракциясвета
совокупность
явлений,
наблюдаемых
при
распространении света сквозь малые отверстия, вблизи границ непрозрачных
тел и т.д., обусловленных волновой природой света, отклонение от законов
геометрической оптикой.
Принцип Гюйгенса-Френеля, волновую поверхность распространяющегося
света можно представить как совокупность бесконечно малых элементов,
являющихся источниками вторичных когерентных сферических волн,
амплитуды которых пропорциональна площади элемента; амплитуда
колебаний в любой точке пространства за волновой поверхностью
определяется интерференцией этих вторичных волн.
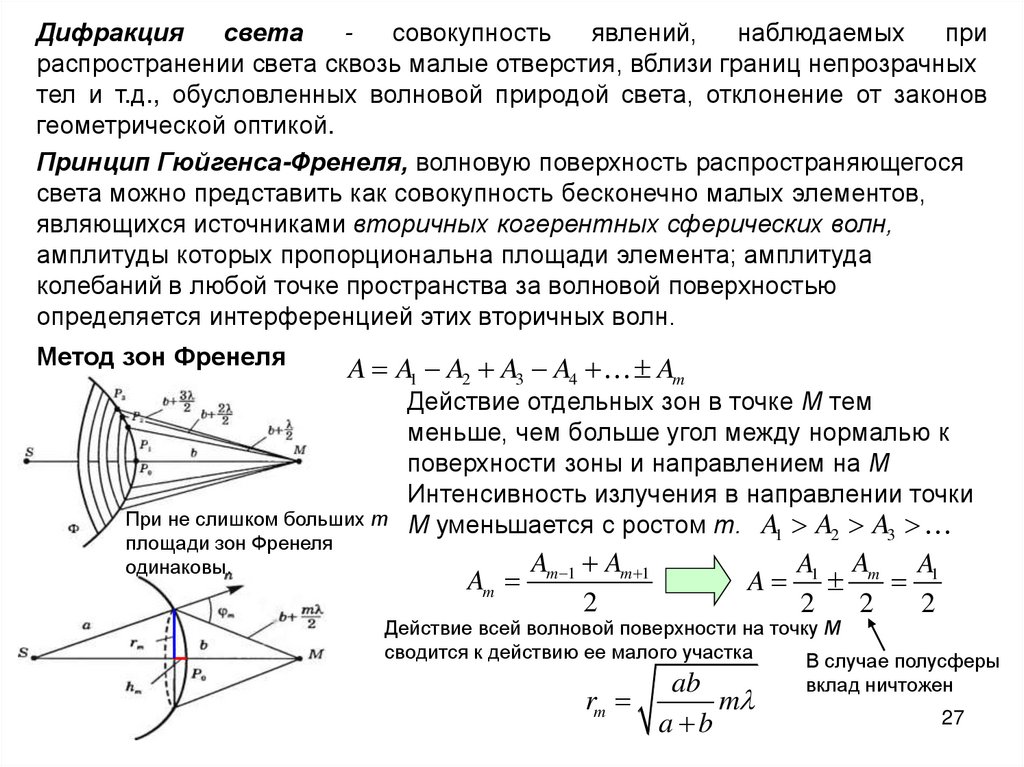
Метод зон Френеля
A A1 A2 A3 A4
При не слишком больших т
площади зон Френеля
одинаковы.
Am
Действие отдельных зон в точке М тем
меньше, чем больше угол между нормалью к
поверхности зоны и направлением на М
Интенсивность излучения в направлении точки
М уменьшается с ростом т. A1 A2 A3
Am
Am 1 Am 1
2
A
A1 Am A1
2
2
2
Действие всей волновой поверхности на точку М
сводится к действию ее малого участка
В случае полусферы
rm
ab
m
a b
вклад ничтожен
27
28.
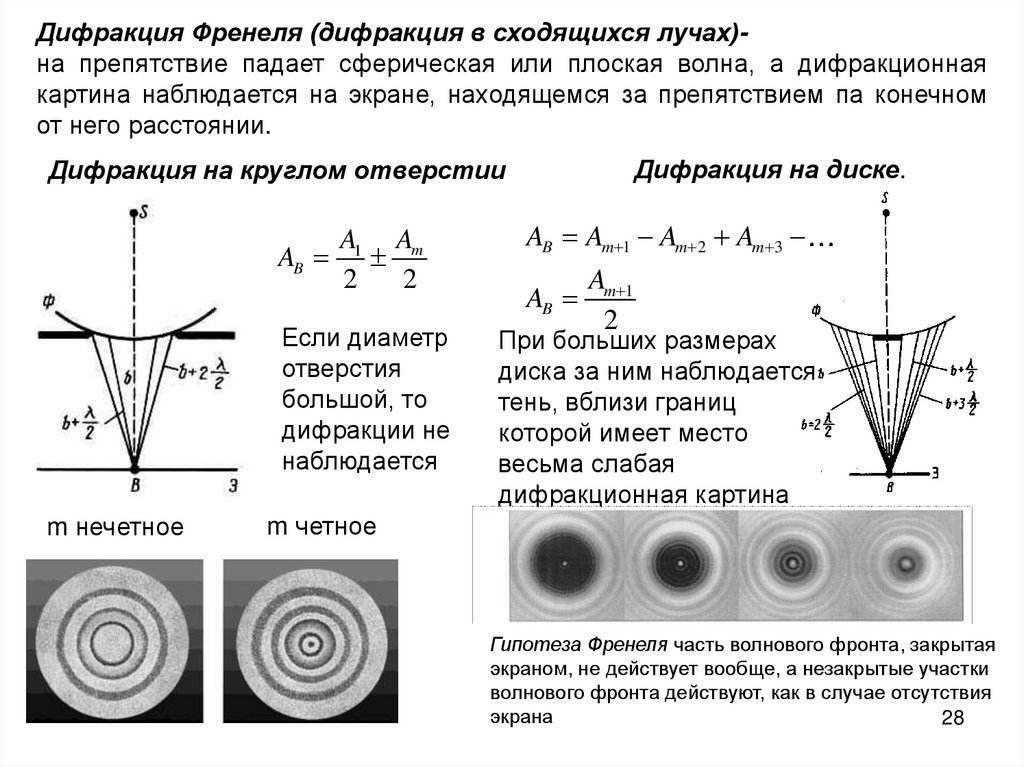
Дифракция Френеля (дифракция в сходящихся лучах)на препятствие падает сферическая или плоская волна, а дифракционнаякартина наблюдается на экране, находящемся за препятствием па конечном
от него расстоянии.
Дифракция на диске.
Дифракция на круглом отверстии
A1 Am
2
2
AB Am 1 Am 2 Am 3
Если диаметр
отверстия
большой, то
дифракции не
наблюдается
При больших размерах
диска за ним наблюдается
тень, вблизи границ
которой имеет место
весьма слабая
дифракционная картина
AB
m нечетное
Am 1
AB
2
m четное
Гипотеза Френеля часть волнового фронта, закрытая
экраном, не действует вообще, а незакрытые участки
волнового фронта действуют, как в случае отсутствия
экрана
28
29.
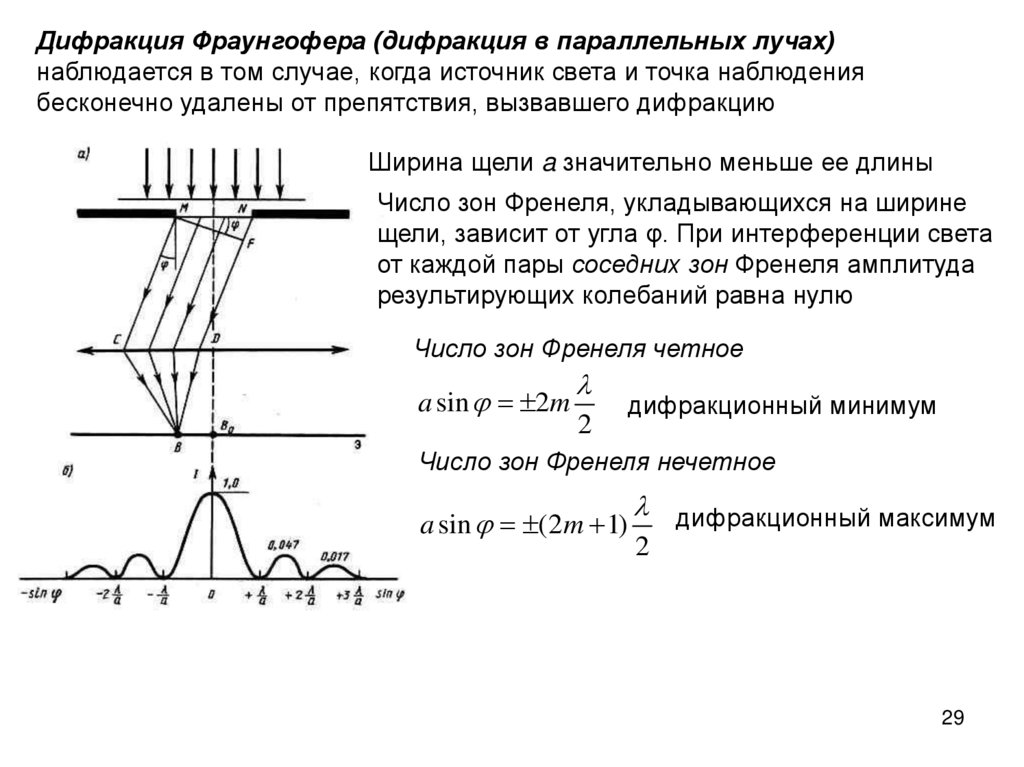
Дифракция Фраунгофера (дифракция в параллельных лучах)наблюдается в том случае, когда источник света и точка наблюдения
бесконечно удалены от препятствия, вызвавшего дифракцию
Ширина щели a значительно меньше ее длины
Число зон Френеля, укладывающихся на ширине
щели, зависит от угла φ. При интерференции света
от каждой пары соседних зон Френеля амплитуда
результирующих колебаний равна нулю
Число зон Френеля четное
a sin 2m
2
дифракционный минимум
Число зон Френеля нечетное
a sin (2m 1)
дифракционный максимум
2
29
30.
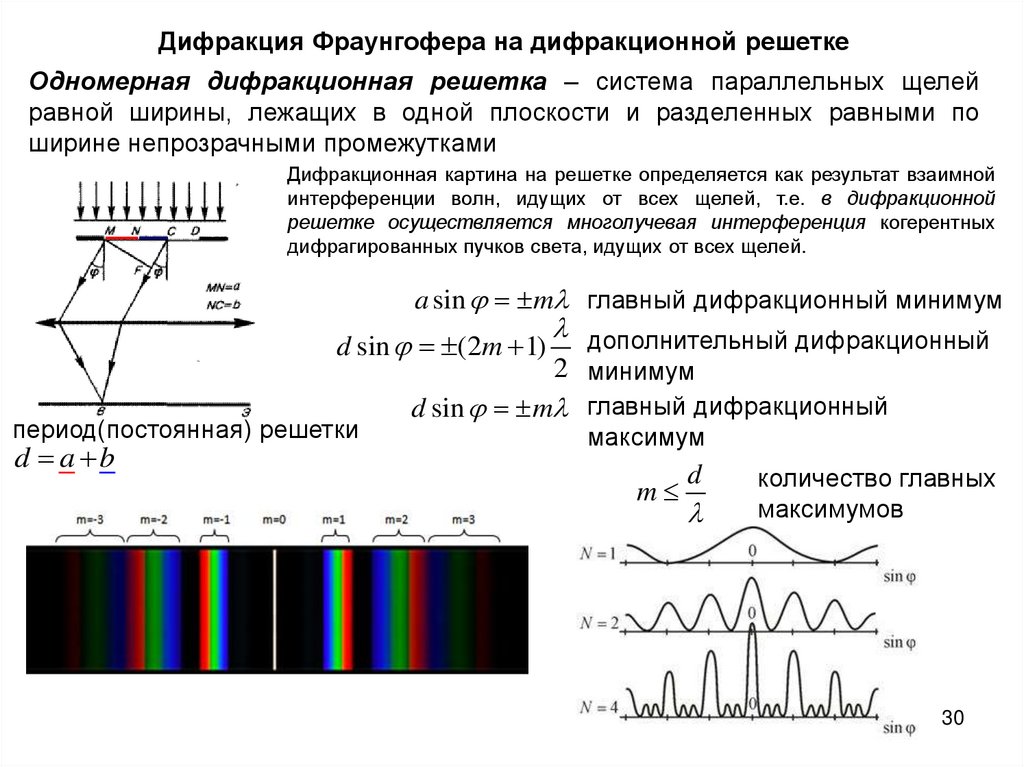
Дифракция Фраунгофера на дифракционной решеткеОдномерная дифракционная решетка – система параллельных щелей
равной ширины, лежащих в одной плоскости и разделенных равными по
ширине непрозрачными промежутками
Дифракционная картина на решетке определяется как результат взаимной
интерференции волн, идущих от всех щелей, т.е. в дифракционной
решетке осуществляется многолучевая интерференция когерентных
дифрагированных пучков света, идущих от всех щелей.
a sin m главный дифракционный минимум
d sin (2m 1)
период(постоянная) решетки
d a b
дополнительный дифракционный
2 минимум
d sin m главный дифракционный
максимум
m
d
количество главных
максимумов
30
31.
Пространственные(трехмерные)
решетки
пространственные
образования, в которых элементы структуры подобны по форме, имеют
геометрически правильное и периодически повторяющееся расположение, а
также постоянные (периоды) решеток, соизмеримые с длиной волны
электромагнитного излучения.
Дифракционные максимумы наблюдаются в тех
направлениях, в которых все отраженные
атомными
плоскостями
волны
будут
находиться в одинаковой фазе
2d sin m
Рентгеноструктурный анализ
формула Вульфа-Брэггов
Рентгеновская спектроскопия
Электронография и нейтронография
31
32.
Дисперсия света - зависимость фазовой скорости v света в среде от егочастоты, или зависимость показателя преломления среды n от частоты света
Следствие дисперсии - разложение в спектр
пучка белого света при прохождении его через
призму
Различия в дифракционном и призматическом
A(n 1)
спектрах
1. Дифракционная решетка разлагает падающий
свет непосредственно по длинам волн поэтому по
измеренным
углам
(по
направлениям
соответствующих максимумов) можно вычислить
длину волны. Разложение света в спектр в призме
происходит по значениям показателя преломления,
поэтому для определения длины волны нужно знать
зависимость n=f(λ)
2. Цвета в дифракционном и призматическом
спектрах располагаются различно.
32
33.
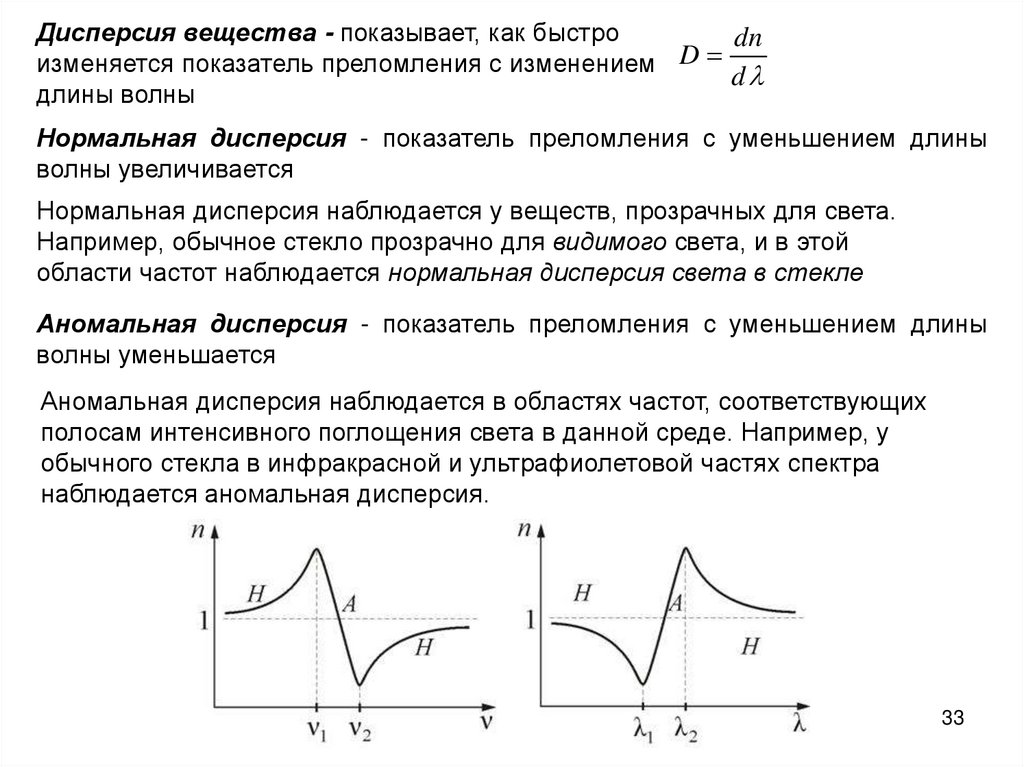
Дисперсия вещества - показывает, как быстроdn
D
изменяется показатель преломления с изменением
d
длины волны
Нормальная дисперсия - показатель преломления с уменьшением длины
волны увеличивается
Нормальная дисперсия наблюдается у веществ, прозрачных для света.
Например, обычное стекло прозрачно для видимого света, и в этой
области частот наблюдается нормальная дисперсия света в стекле
Аномальная дисперсия - показатель преломления с уменьшением длины
волны уменьшается
Аномальная дисперсия наблюдается в областях частот, соответствующих
полосам интенсивного поглощения света в данной среде. Например, у
обычного стекла в инфракрасной и ультрафиолетовой частях спектра
наблюдается аномальная дисперсия.
33
34.
Поглощением (абсорбцией) света называется явление уменьшения энергиисветовой волны при распространении в веществе вследствие преобразования
энергии волны в другие виды энергии. В результате поглощения интенсивность
света при прохождении через вещество уменьшается.
I I 0 e x
Закон Бугера
коэффициент поглощения α зависит
от длины волны света, химической
природы и состояния вещества и не
зависит от интенсивности света
Линейчатый спектр поглощения
одноатомные газы и пары металлов
Широкие полосы поглощения
диэлектрики
Металлы имеют большой коэффициент
поглощения - для света непрозрачны
Натрий
Зависимостью коэффициента
поглощения от длины волны
объясняется окрашенность
поглощающих тел. Например,
стекло, слабо поглощающее
красные и оранжевые лучи и
сильно поглощающее зеленые и
синие, при освещении белым
светом будет казаться красным.
Водород
Гелий
34
35.
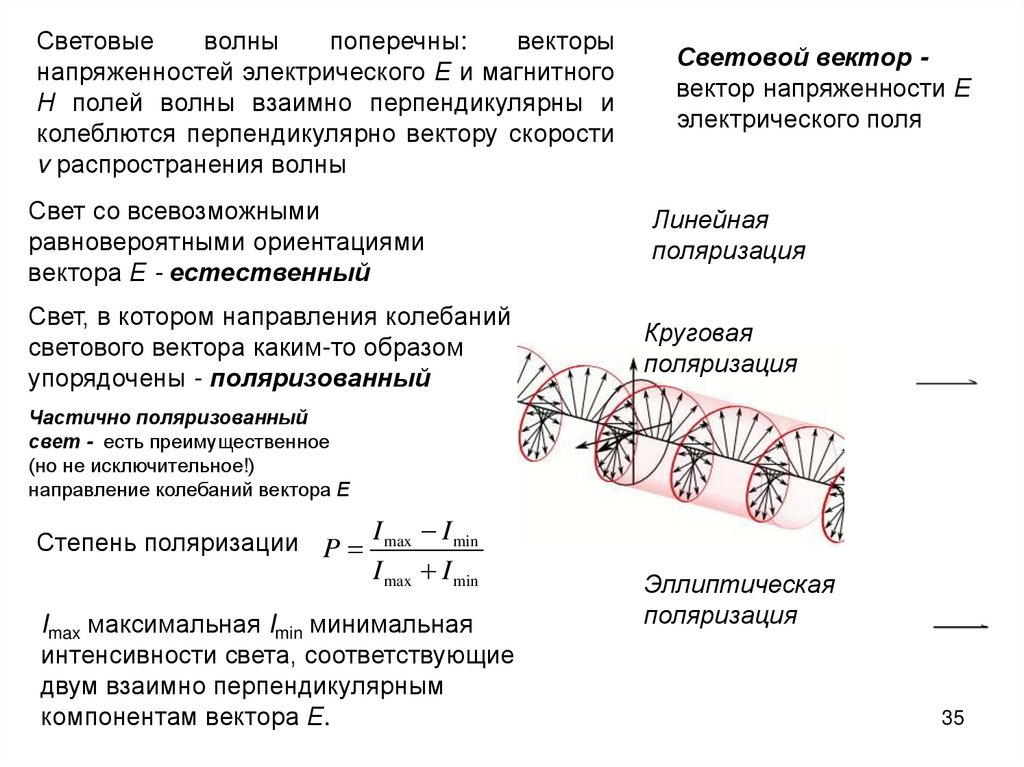
Световыеволны
поперечны:
векторы
напряженностей электрического Е и магнитного
Н полей волны взаимно перпендикулярны и
колеблются перпендикулярно вектору скорости
v распространения волны
Световой вектор вектор напряженности Е
электрического поля
Свет со всевозможными
равновероятными ориентациями
вектора Е - естественный
Линейная
поляризация
Свет, в котором направления колебаний
светового вектора каким-то образом
упорядочены - поляризованный
Круговая
поляризация
Частично поляризованный
свет - есть преимущественное
(но не исключительное!)
направление колебаний вектора Е
Степень поляризации P I max I min
I max I min
Imax максимальная Imin минимальная
интенсивности света, соответствующие
двум взаимно перпендикулярным
компонентам вектора Е.
Эллиптическая
поляризация
35
36.
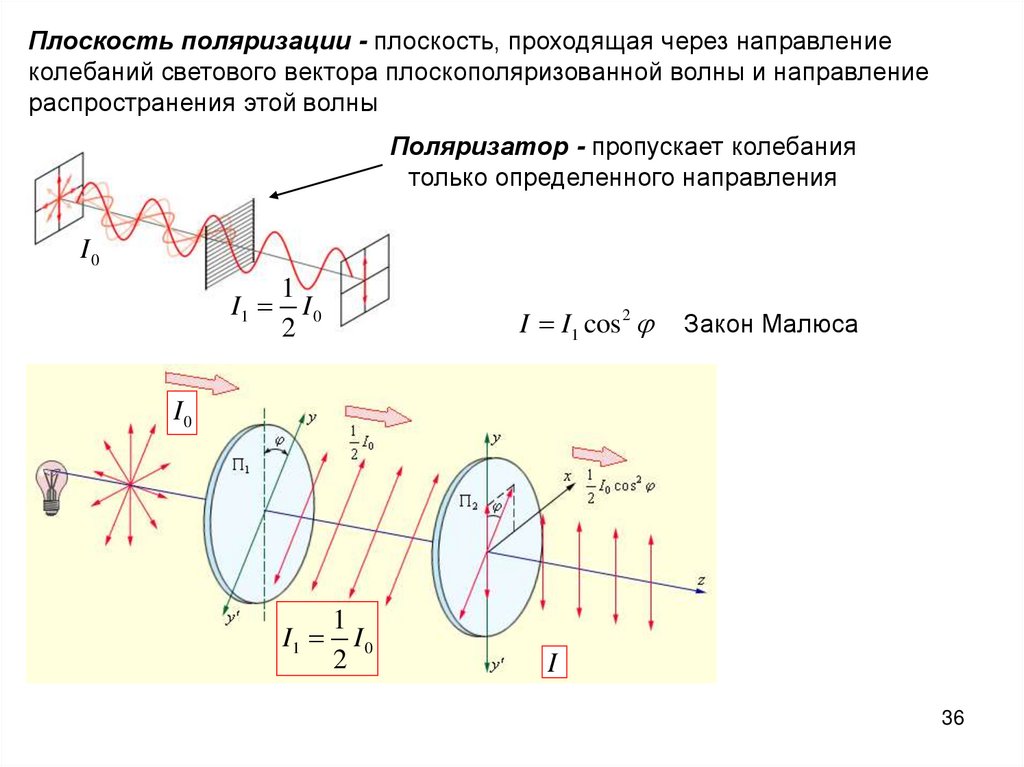
Плоскость поляризации - плоскость, проходящая через направлениеколебаний светового вектора плоскополяризованной волны и направление
распространения этой волны
Поляризатор - пропускает колебания
только определенного направления
I0
I1
1
I0
2
I I1 cos 2
Закон Малюса
I0
I1
1
I0
2
I
36
37.
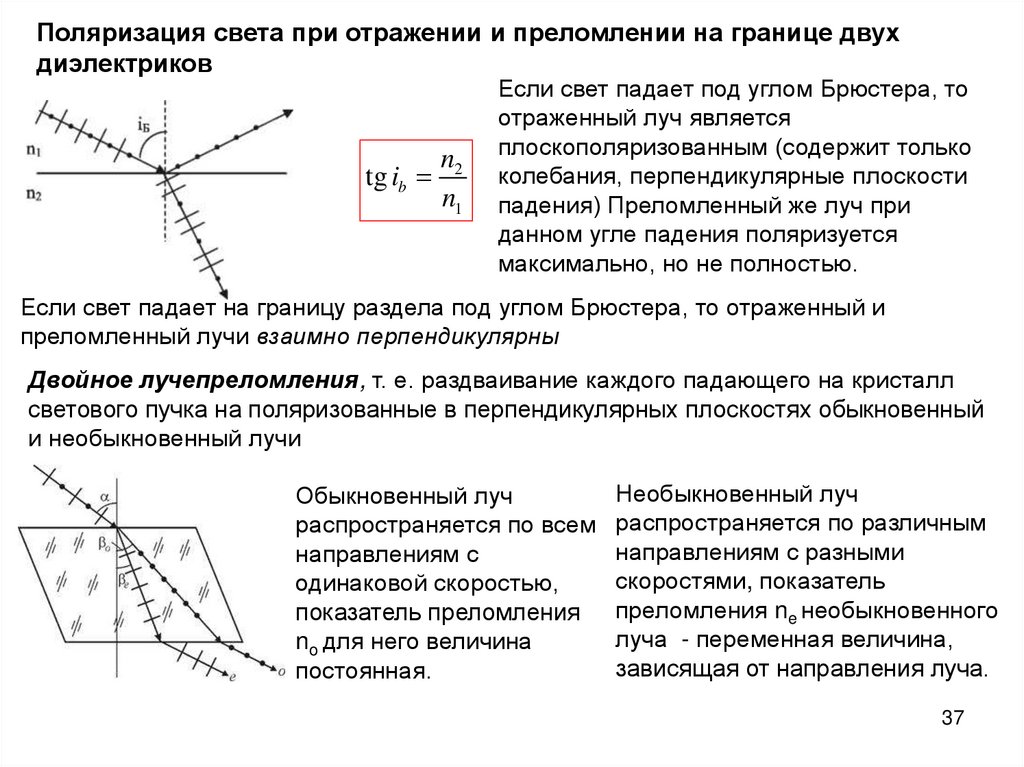
Поляризация света при отражении и преломлении на границе двухдиэлектриков
tg ib
n2
n1
Если свет падает под углом Брюстера, то
отраженный луч является
плоскополяризованным (содержит только
колебания, перпендикулярные плоскости
падения) Преломленный же луч при
данном угле падения поляризуется
максимально, но не полностью.
Если свет падает на границу раздела под углом Брюстера, то отраженный и
преломленный лучи взаимно перпендикулярны
Двойное лучепреломления, т. е. раздваивание каждого падающего на кристалл
светового пучка на поляризованные в перпендикулярных плоскостях обыкновенный
и необыкновенный лучи
Обыкновенный луч
распространяется по всем
направлениям с
одинаковой скоростью,
показатель преломления
no для него величина
постоянная.
Необыкновенный луч
распространяется по различным
направлениям с разными
скоростями, показатель
преломления ne необыкновенного
луча - переменная величина,
зависящая от направления луча.
37
38.
3839.
Методы получения искусственной оптической анизотропииМера возникающей анизотропии
1) одностороннее сжатие или растяжение
(кристаллы кубической системы, стекла и др.);
2) действие электрического поля - эффект Керра
(жидкости, аморфные тела, газы);
3) действие магнитного поля (жидкости, стекла,
коллоиды).
no ne k1
no ne k2 E 2
no ne k3 H 2
Вращение плоскости поляризации
Оптически активные вещества твердые тела
d
обладают способностью вращать
Cd
растворы
плоскость поляризации
удельное вращение
Правовращающие - плоскость
поляризации, если смотреть навстречу
Вращение плоскости поляризации в
лучу, вращается вправо (по часовой
оптически неактивных веществах,
стрелке)
возникающее под действием
Левовращающие - плоскость
магнитного поля - эффект
поляризации, если смотреть навстречу
Фарадея (магнитное вращения
лучу, вращается влево (против часовой
плоскости поляризации).
39
стрелки)
40.
Тепловое излучение – излучение, обусловленное нагреванием, совершаетсяза счет энергии теплового движения атомов и молекул вещества (т. е. за счет
его внутренней энергии) и свойственно всем телам при температуре выше 0 К.
сплошной спектр
равновесное
dW
R ,T
спектральная плотность энергетической светимости
d
(излучательности) тела - мощность излучения с единицы
2
площади поверхности тела в интервале частот единичной ширины R ,T R ,T
c
dW энергия электромагнитного излучения, испускаемого за единицу
времени (мощность излучения) с единицы площади поверхности тела в
интервале частот от до d
интегральная энергетическая
энергетическая R R d
T
,T
светимость
светимость тела
0
(интегральная излучательность)
спектральная поглощательная способность - доля энергии,
dWпогл
A
приносимой за единицу времени на единицу площади поверхности
,T
dWпад
тела падающими на нее электромагнитными волнами с частотами
от до d , поглощаемая телом
A ,T 1
Абсолютно черное тело – тело, способное полностью, при любой
температуре, поглощать все падающее на него излучение любой частоты
Серое тело – поглощательная способность одинакова для всех частот, A 1
,T
зависит только от температуры, материала и состояния поверхности
40
41.
Закон Кирхгофа - отношение спектральной плотности энергетическойсветимости к спектральной поглощательной способности не зависит от
природы тела; оно является для всех тел универсальной функцией частоты
(длины волны) и температуры R ,T
A ,T
r ,T
универсальная функция Кирхгофа - спектральная
плотность энергетической светимости черного тела
R R (T ) r ,T d энергетическая светимость черного тела
0
R T 4
Закон Стефана-Больцмана
Закон смещения Вина
max
для черного тела
R T 4 для серого тела
b
T
Длина волны, соответствующая
максимальному значению спектральной
плотности энергетической светимости
черного тела
41
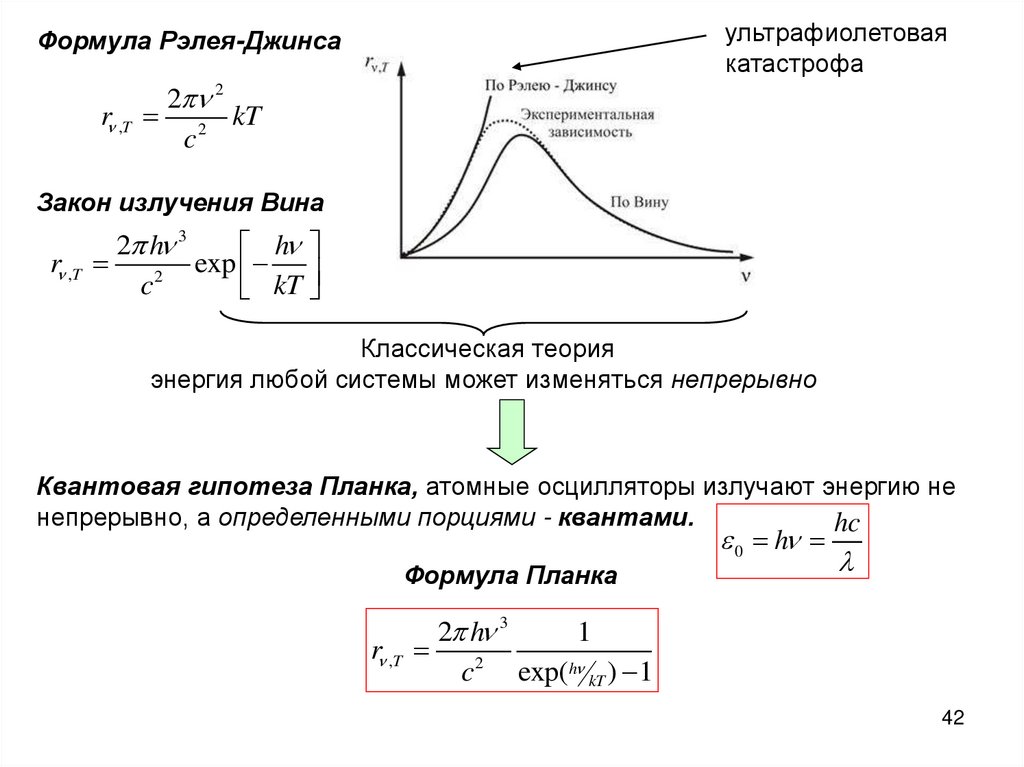
42.
ультрафиолетоваякатастрофа
Формула Рэлея-Джинса
2 2
r ,T 2 kT
c
Закон излучения Вина
2 h 3
h
r ,T
exp
c2
kT
Классическая теория
энергия любой системы может изменяться непрерывно
Квантовая гипотеза Планка, атомные осцилляторы излучают энергию не
непрерывно, а определенными порциями - квантами.
hc
0 h
Формула Планка
2 h 3
1
r ,T
c 2 exp(h kT ) 1
42
43.
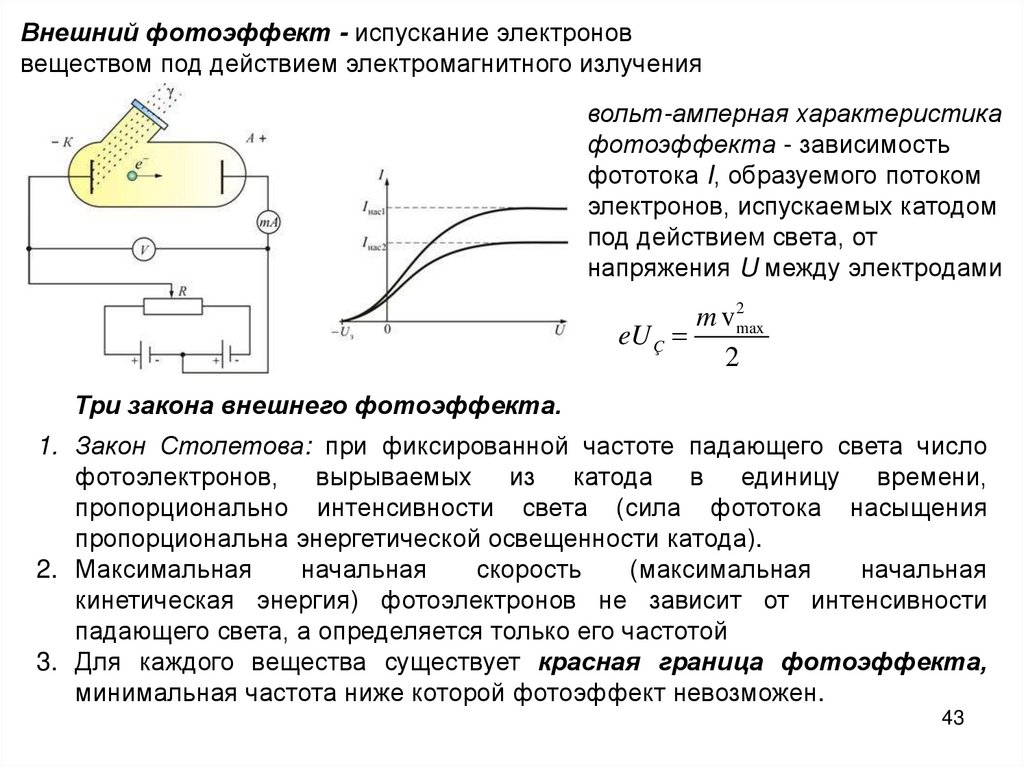
Внешний фотоэффект - испускание электроноввеществом под действием электромагнитного излучения
вольт-амперная характеристика
фотоэффекта - зависимость
фототока I, образуемого потоком
электронов, испускаемых катодом
под действием света, от
напряжения U между электродами
m v 2max
eU Ç
2
Три закона внешнего фотоэффекта.
1. Закон Столетова: при фиксированной частоте падающего света число
фотоэлектронов, вырываемых из катода в единицу времени,
пропорционально интенсивности света (сила фототока насыщения
пропорциональна энергетической освещенности катода).
2. Максимальная
начальная
скорость
(максимальная
начальная
кинетическая энергия) фотоэлектронов не зависит от интенсивности
падающего света, а определяется только его частотой
3. Для каждого вещества существует красная граница фотоэффекта,
минимальная частота ниже которой фотоэффект невозможен.
43
44.
Эйнштейн:Свет не только испускается, но и распространяется в пространстве и
поглощается веществом отдельными порциями (квантами)
Квант электромагнитного излучения -фотон
Уравнение Эйнштейна для внешнего фотоэффекта
энергия фотона
m v 2max
h A
2
кинетическая энергия
электрона
работа выхода
электрона из вещества
красная граница фотоэффекта
v 0,
0
A
h
Внутренний фотоэффект - переходы электронов внутри полупроводника
или диэлектрика из связанных состояний в свободные без вылета наружу, а
значит повышение проводимости при освещении или возникновение ЭДС.
Вентильный фотоэффект, разновидность внутреннего, - возникновение
ЭДС (фото-ЭДС) при освещении контакта двух разных полупроводников или
полупроводника и металла (при отсутствии внешнего электрического поля).
44
45.
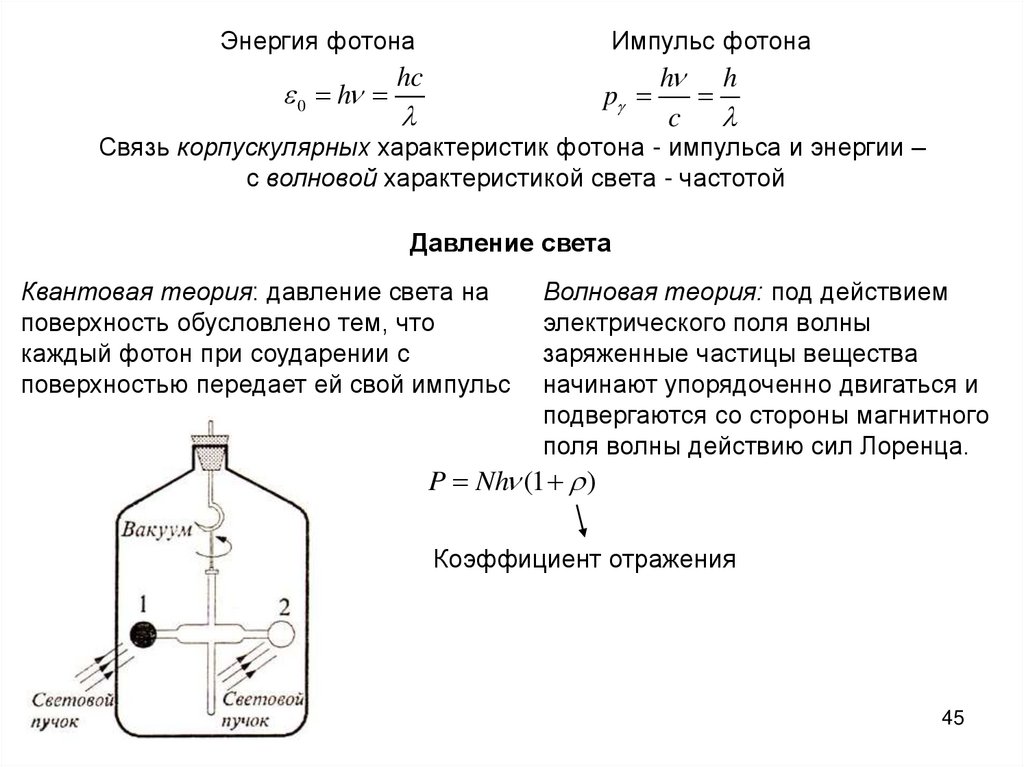
Энергия фотона0 h
Импульс фотона
hc
p
h h
c
Связь корпускулярных характеристик фотона - импульса и энергии –
с волновой характеристикой света - частотой
Давление света
Квантовая теория: давление света на
поверхность обусловлено тем, что
каждый фотон при соударении с
поверхностью передает ей свой импульс
Волновая теория: под действием
электрического поля волны
заряженные частицы вещества
начинают упорядоченно двигаться и
подвергаются со стороны магнитного
поля волны действию сил Лоренца.
P Nh (1 )
Коэффициент отражения
45
46.
Эффект Комптона – упругое рассеяние коротковолновогоэлектромагнитного излучения (рентгеновского и гамма-излучений) на
свободных (или слабосвязанных) электронах вещества, сопровождающееся
увеличением длины волны
h
(1 cos )
m0 c
Электромагнитное излучение, обладает одновременно корпускулярными и
волновыми свойствами
волновые свойства: закономерности
распространения, интерференция,
дифракция, поляризация
трудно обнаружить при больших
энергиях / малых длинах волн
корпускулярные свойства: процессы
взаимодействия света с веществом
трудно обнаружить при больших
длинах волн/ малых энергиях
46
47.
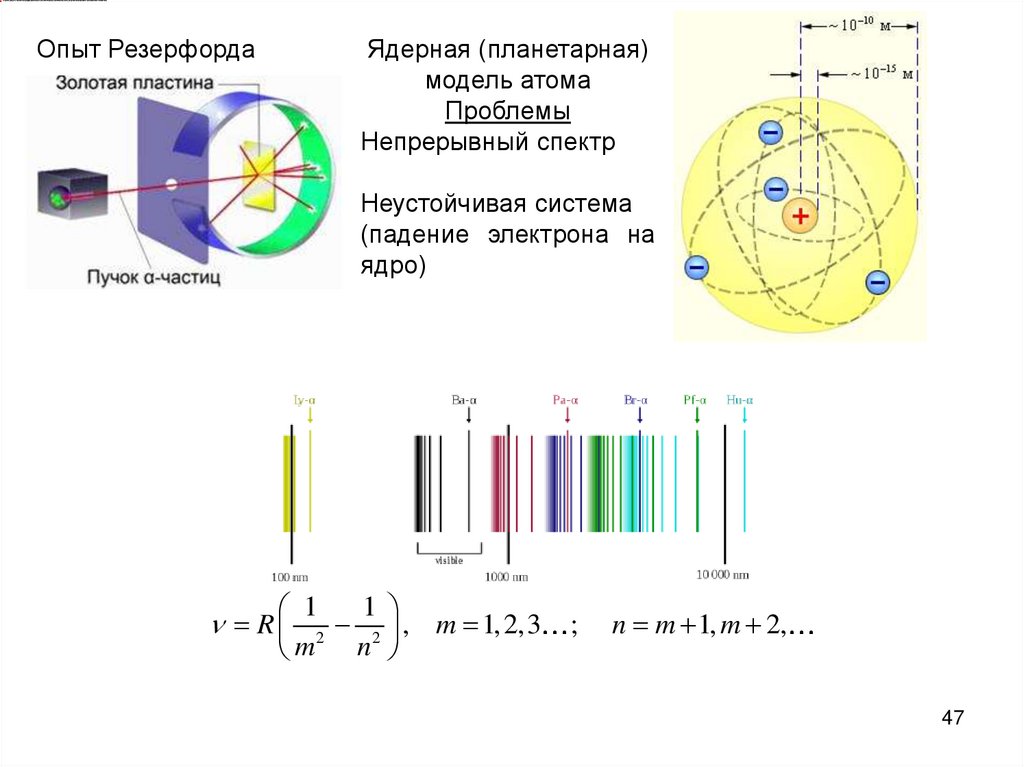
Опыт РезерфордаЯдерная (планетарная)
модель атома
Проблемы
Непрерывный спектр
Неустойчивая система
(падение электрона на
ядро)
1
1
, m 1, 2,3
2
2
m n
R
;
n m 1, m 2,
47
48.
Первый постулат Бора (постулат стационарных состояний):в атоме существуют стационарные (не изменяющиеся со временем) состояния, в
которых он не излучает энергии; эти состояния характеризуются определенными
дискретными значениями энергии.
Уравнение круговых m v r n h
стационарных орбит
2
Второй постулат Бора (правило частот): при переходе электрона с одной
стационарной орбиты на другую излучается (поглощается) один фотон с энергией равной
разности энергий соответствующих стационарных состояний
h E E
экспериментальное подтверждение - опыты Франка и Герца
n
m
Спектр атома водорода по Бору
rn n
4 0
me Ze2
2
2
радиус стационарных орбит
Последовательность
энергетических уровней
1 Z 2 me e4
En 2
n 8h 2 02
главное квантовое число
Z 2 me e4 1
1
8h3 02 m2 n 2
Недостатки
внутренние противоречия: применение
законов классической физики, при
базировании на квантовых постулатах.
невозможность описания спектра атома
гелия
нет объяснения интенсивности линий и
причины переходов
48
49.
Универсальность корпускулярно-волнового дуализма: не только фотоны, но иэлектроны и любые другие частицы материи наряду с корпускулярными обладают также
волновыми свойствами
Любой частице, обладающей импульсом, сопоставляют волновой процесс, длина волны
которого определяется по формуле де Бройля
h
Подтверждение - дифракция электронов, нейтронов, протонов,
атомных и молекулярных пучков
p
«Для атомного объекта существует потенциальная возможность проявлять себя, в
зависимости от внешних условий, либо как волна, либо как частица, либо
промежуточным образом. Именно в этой потенциальной возможности различных
проявлений свойств, присущих микрообъекту, и состоит дуализм «волна -частица»» В.А.
Фок
Соотношения неопределенностей Гейзенберга
Для микрочастицы не существует
x p x h
состояний, в которых ее координаты и
импульс имели бы одновременно точные y p y h
значения
h
x v x
m
Чем больше масса частицы, тем меньше
неопределенности ее координаты и
скорости и, с тем большей точностью
можно применять к этой частице
понятие траектории
z p z h
соотношение
неопределенностей - квантовое
ограничение применимости
классической механики к
микрообъектам.
E t h
Система, имеющая среднее время жизни Δt,
не может быть охарактеризована
определенным значением энергии; разброс
энергии возрастает с уменьшением среднего
49
времени жизни.
50.
Важнейшая отличительная особенность квантовой теории – вероятностныйподход к описанию микрочастиц
В квантовой механике состояние микрочастиц описывается с помощью
волновой функции,
(r , t ) которая является основным носителем
информации об их корпускулярных и волновых свойствах.
Вероятность нахождения частицы в
элементе объемом dV
dW dV
2
физический смысл имеет не сама
волновая функция, а квадрат ее
модуля, которым задается
интенсивность волн де Бройля.
Ограничения для волновой функции:
конечность (вероятность не может быть больше единицы)
однозначность (вероятность не может быть неоднозначной величиной)
непрерывность (вероятность не может изменяться скачком).
Принципу суперпозиции: если система может находиться в различных
состояниях, описываемых волновыми функциями 1 , 2 , n то она
также может находиться в состоянии , описываемом линейной комбинацией
этих функций:
Cn n
50
51.
Основное уравнение нерелятивистской квантовой механики –уравнение Шредингера
справедливо для любой
нерелятивистской частицы со
спином, равным 0.
2
2m
U (r , t ) i
t
потенциальная функция частицы в
силовом поле, в котором она движется
Уравнение Шредингера для стационарных состояний - состояний с
фиксированными значениями энергии если силовое поле, в котором частица
движется, стационарно, т.е. U≠ U(t) и имеет смысл потенциальной энергии.
(r , t ) (r ) exp iEt /
2
2m
U E
Решения этого уравнения имеют место лишь при определенных значениях
параметра Е, характерных для данной задачи. Эти значения энергии
называются собственными. Соответствующие решения называются
собственными функциями. Собственные значения Е могут образовывать
как непрерывный, так и дискретный ряд. В первом случае говорят о
непрерывном, или сплошном, спектре, во втором - о дискретном
спектре.
51
52.
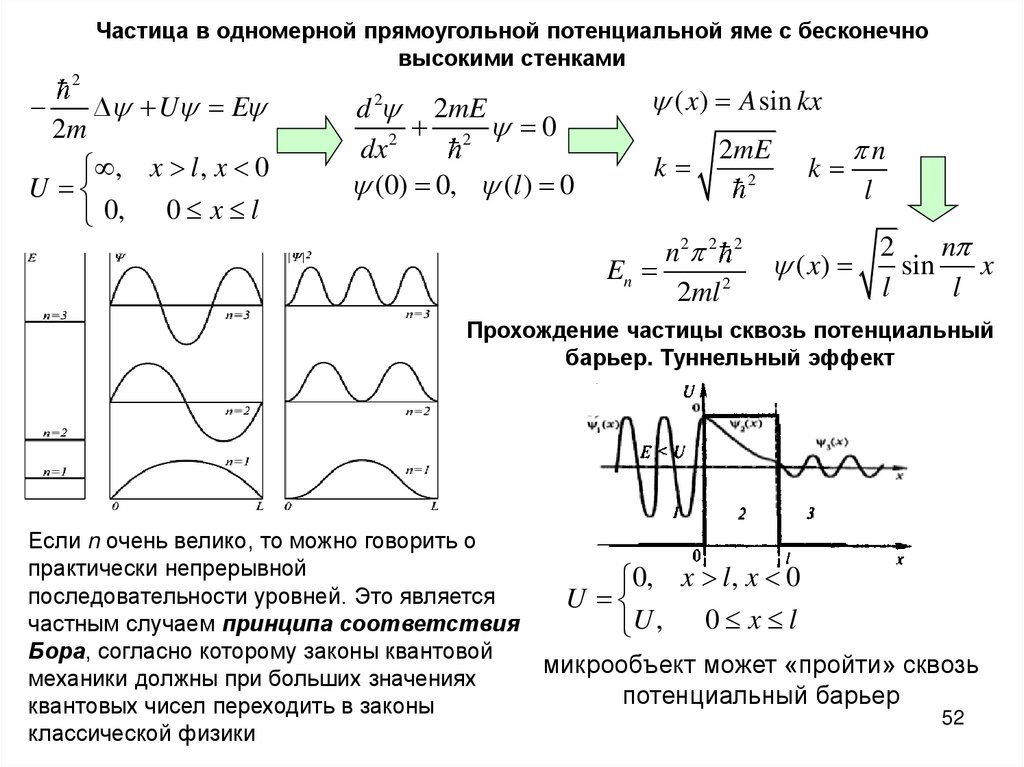
Частица в одномерной прямоугольной потенциальной яме с бесконечновысокими стенками
2
U E
2m
, x l , x 0
U
0, 0 x l
d 2 2mE
2 0
dx 2
(0) 0, (l ) 0
( x) A sin kx
k
2mE
n 2 2 2
En
2ml 2
k
2
n
l
( x)
2
n
sin
x
l
l
Прохождение частицы сквозь потенциальный
барьер. Туннельный эффект
Если n очень велико, то можно говорить о
практически непрерывной
последовательности уровней. Это является
частным случаем принципа соответствия
Бора, согласно которому законы квантовой
механики должны при больших значениях
квантовых чисел переходить в законы
классической физики
0, x l , x 0
U
U , 0 x l
микрообъект может «пройти» сквозь
потенциальный барьер
52
53.
Атом водорода в квантовой механикезадача о движении электрона в кулоновском поле ядра
2
2m
U E
Ze 2
U U (r )
4 0 r
1 Z 2 me4
En 2
n 8h 2 02
Е1 - минимальной возможная энергия, основной
уровень, все остальные- возбужденные
Е < 0 движение электрона связанное - он находится
внутри потенциальной ямы
Е > 0 движение электрона является свободным;
область непрерывного спектра соответствует
ионизованному атому
Главное квантовое число n
Момент импульса (механический
определяет энергетические
орбитальный момент) электрона
уровни электрона n=1,2,3…
квантуется L
l (l 1)
Орбитальное квантовое число
определяет момент импульса
Проекция вектора момента импульса
электрона в атоме
электрона принимает квантованные
l =1,2,.., n-1
значения
Lz m
Магнитное квантовое число определяет
проекцию момента импульса электрона на
заданное направление m = 0, ± 1, ±2,… ±l
53
54.
Частицы обладают собственным неуничтожимымLs s(s 1) Ls , z ms
механическим моментом импульса, не связанным с
движением в пространстве - спином
s - спиновое квантовое число
Спин - квантовая величина, у нее нет
ms - магнитное спиновое квантовое число
классического аналога; это внутреннее
неотъемлемое свойство частицы, подобное
заряду и массе
Тождественные частицы
– частицы с одинаковыми
физическими свойствами
Принцип неразличимости тождественных частиц –
невозможно экспериментально различить тождественные
частицы
Частицы с полуцелым спином (электроны,
протоны, нейтроны) описываются
антисимметричными волновыми
функциями, подчиняются статистике
Ферми-Дирака и называются
фермионами.
Частицы с нулевым или целым спином (πмезоны, фотоны) описываются
симметричными волновыми функциями,
подчиняются статистике БозеЭйнштейна и называются бозонами
квантово-механическая формулировка принципа Паули: системы фермионов
встречаются в природе только в состояниях, описываемых антисимметричными
волновыми функциями
в системе одинаковых фермионов любые
два из них не могут одновременно
находиться в одном и том же состоянии.
в одном и том же атоме не может быть
более одного электрона с одинаковым
набором четырех квантовых чисел n, l, m, ms
54
55.
Молекула является квантовой системой; описывается уравнением Шредингера,учитывающим движение электронов в молекуле, колебания атомов молекулы,
вращение молекулы
энергия вращения ядер
E Eэл Eкол Eвр
энергия движения электронов энергия колебаний ядер
относительно ядер
Каждая из энергий квантуется и определяется квантовыми числами. При переходе из
одного энергетического состояния в другое поглощается или испускается энергия
ΔЕ= hv. При таких переходах одновременно изменяются энергия движения электронов,
энергии колебаний и вращения ядер
Молекулярные спектры –
спектры излучения (поглощения),
возникающих при квантовых
переходах между уровнями
энергии молекул
Типичные молекулярные спектры полосатые, представляют собой
совокупность более или менее узких
полос. Структура спектров различна
для разных молекул и с увеличением
числа атомов в молекуле усложняется
Комбинационное рассеяние света: если на вещество падает строго
монохроматический свет, то в спектре рассеянного света помимо
несмещенной спектральной линии обнаруживаются новые линии, частоты
которых представляют собой суммы или разности частоты падающего света и
частот собственных колебаний (или вращений) молекул рассеивающей среды.
55
56.
Атомы могут находиться лишь в квантовых состояниях с дискретнымизначениями энергии
Процесс испускания фотона
возбужденным атомом без какихлибо внешних воздействий спонтанное излучение.
Это излучение не когерентно
вынужденное излучение строго
когерентно с вынуждающим
излучением, т.е. испущенный фотон
неотличим от фотона, падающего на
атом излучением
Чтобы среда усиливала падающее на
нее излучение, необходимо создать
неравновесное состояние системы,
при котором число атомов в
возбужденных состояниях было бы
больше, чем их число в основном
состоянии
Если на атом, находящийся в
возбужденном состоянии действует
внешнее излучение с частотой,
удовлетворяющей условию перехода
в основное состояние, то возникает
вынужденный переход в основное
состояние с излучением фотона той
же частоты
Лазеры!
Свойства:
1. Временная и пространственная
когерентность
2. Строгая монохроматичность
3. Большая плотность потока
энергии.
4. Очень малое угловое
расхождение в пучке
56
57.
Адиабатическое приближение: Квантово-механическая система разделяетсяна тяжелые и легкие частицы - ядра и электроны. Поскольку массы и скорости
этих частиц значительно различаются, можно считать, что движение
электронов происходит в поле неподвижных ядер, а медленно движущиеся
ядра находятся в усредненном поле всех электронов
Приближение самосогласованного поля: Взаимодействие данного электрона
со всеми другими электронами заменяется действием на него стационарного
электрического поля, обладающего периодичностью кристаллической решетки
Зонная теория твердого тела
взаимодействие между атомами приводит к тому, что энергетические уровни
атомов смещаются, расщепляются и расширяются в зоны, образуется
зонный энергетический спектр
Энергия внешних электронов
В твердых телах внутренние электроны ведут себя
может принимать значения в
так же, как в изолированных атомах, валентные же
пределах областей, называемых
электроны «коллективизированы» - принадлежат
всему твердому телу.
разрешенными
энергетическими зонами
Разрешенные энергетические зоны разделены зонами запрещенных
значений энергии, называемыми запрещенными энергетическими
зонами. В них электроны находиться не могут
57
58.
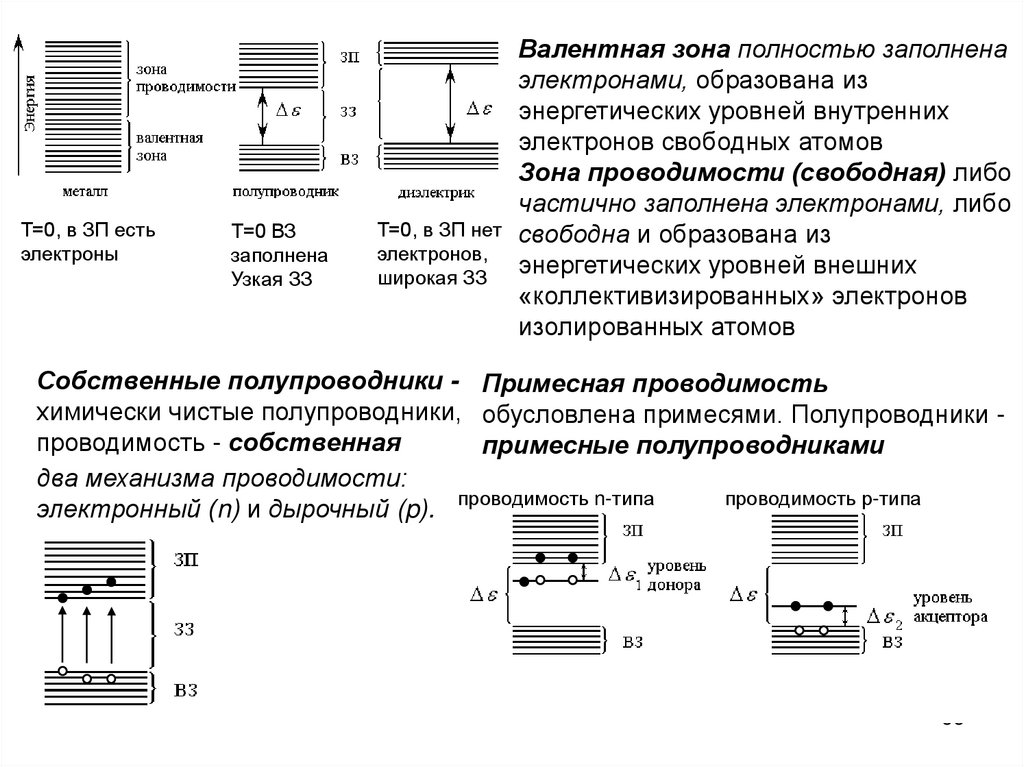
Т=0, в ЗП естьэлектроны
Т=0 ВЗ
заполнена
Узкая ЗЗ
Валентная зона полностью заполнена
электронами, образована из
энергетических уровней внутренних
электронов свободных атомов
Зона проводимости (свободная) либо
частично заполнена электронами, либо
Т=0, в ЗП нет свободна и образована из
электронов,
энергетических уровней внешних
широкая ЗЗ
«коллективизированных» электронов
изолированных атомов
Собственные полупроводники - Примесная проводимость
химически чистые полупроводники, обусловлена примесями. Полупроводники проводимость - собственная
примесные полупроводниками
два механизма проводимости:
проводимость р-типа
электронный (n) и дырочный (p). проводимость n-типа
58
59.
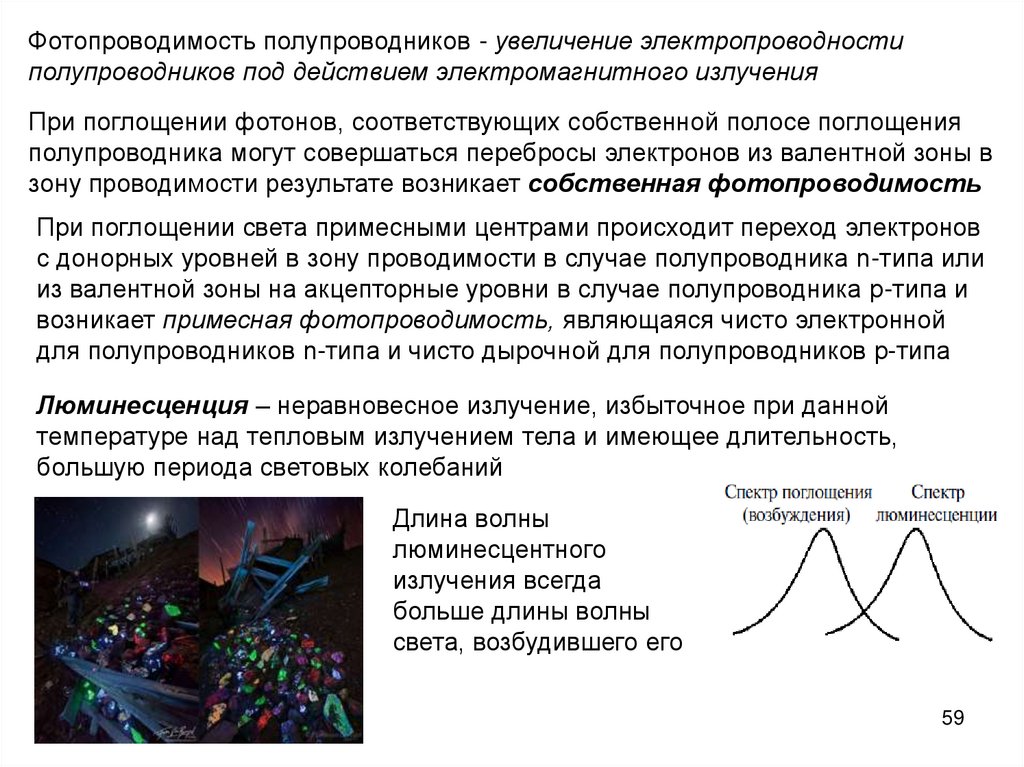
Фотопроводимость полупроводников - увеличение электропроводностиполупроводников под действием электромагнитного излучения
При поглощении фотонов, соответствующих собственной полосе поглощения
полупроводника могут совершаться перебросы электронов из валентной зоны в
зону проводимости результате возникает собственная фотопроводимость
При поглощении света примесными центрами происходит переход электронов
с донорных уровней в зону проводимости в случае полупроводника n-типа или
из валентной зоны на акцепторные уровни в случае полупроводника р-типа и
возникает примесная фотопроводимость, являющаяся чисто электронной
для полупроводников n-типа и чисто дырочной для полупроводников р-типа
Люминесценция – неравновесное излучение, избыточное при данной
температуре над тепловым излучением тела и имеющее длительность,
большую периода световых колебаний
Длина волны
люминесцентного
излучения всегда
больше длины волны
света, возбудившего его
59
60.
AZ
X
Общее число нуклонов в атомном ядре массовое число А.
Заряд ядра Ze, Z - зарядовое число
ядра, равное числу протонов (и
электронов) в ядре и совпадающее с
порядковым номером химического
элемента в Периодической системе
элементов
Изотопы - ядра с одинаковыми Z, но разными А
1
1
H , 12 H , 12 H
Изобары -ядра с одинаковыми А, но разными Z
10
4
10
Be, 10
B,
5
6 C
Масса ядра меньше, чем сумма масс составляющих его нуклонов
Энергия, которую нужно затратить, чтобы расщепить ядро на отдельные
Нуклоны - энергией связи ядра E Zm (A Z)m m c 2
H
n
am
m Zm p (A Z)mn mя дефект массы ядра
60
61.
Между составляющими ядро нуклонами действуют специфические для ядрасилы, значительно превышающие кулоновские силы отталкивания между
протонами - ядерные силы, относящиеся к классу сильных взаимодействий
Свойства ядерных сил
1) силы притяжения;
2) короткодействующими (10-15 м).
3) зарядовая независимость, т.е. имеют
неэлектрическую природу
4) насыщение, т. е. каждый нуклон в
ядре взаимодействует только с
ограниченным числом ближайших к
нему нуклонов
5) зависят от взаимной ориентации
спинов взаимодействующих нуклонов
6) не являются центральными
Капельная модель ядра
Ядро рассматривается как капля
электрически заряженной
несжимаемой жидкости (с
плотностью, равной ядерной),
подчиняющуюся законам
квантовой механики
Оболочечная модель ядра
Распределение нуклонов в ядре по
дискретным энергетическим уровням
(оболочкам), заполняемым нуклонами
согласно принципу Паули
61
62.
Радиоактивность - способность некоторых атомных ядерсамопроизвольно превращаться в другие ядра с испусканием различных
видов радиоактивных излучений
α-излучение – поток ядер гелия,
β-излучение - поток быстрых электронов,
обладает высокой ионизирующей
ионизирующая способность значительно
способностью и малой
меньше (примерно на два порядка), а
проникающей способностью
проникающая способность гораздо больше
α -частиц
γ-излучение - электромагнитное
излучение с чрезвычайно малой длиной
Закон радиоактивного распада
волны λ< 10-10 м, т.е. является потоком
фотонов, ионизирующая способность
N N 0 e t
относительно слабая, проникающая
способность очень большая
постоянная радиоактивного распада
Период полураспада Т1/2 - время, за
ln 2
которое исходное число радиоактивных T1/ 2
ядер в среднем уменьшается вдвое
среднее время жизни радиоактивного ядра
Правила смещения
A
Z
X ZA 42 Y 24 He
α-распад
A
Z
X ZA 1 Y 0 1 e
β-распад
1
Активность
A
dN
N
dt
62
63.
Ядерные реакции - превращения атомных ядер при взаимодействии сэлементарными частицами или друг с другом
выполняются законы сохранения
выполняются законы сохранения
зарядовых и массовых чисел
энергии, импульса и момента импульса
Классификация
- по роду участвующих частиц
- по энергии вызывающих их частиц
- по роду участвующих в них ядер
(легкие,средние,тяжелые)
- по характеру ядерных превращений
цепная реакция деления: частицы,
вызывающие реакцию, образуются как
продукты этой реакции
коэффициент размножения отношение
числа нейтронов в данном поколении к их
числу в предыдущем поколении
критическая масса - минимальная масса
делящегося вещества, находящегося в
системе критических размеров, необходимая
для осуществления цепной реакции
реакция деления ядра: тяжелое ядро
под действием нейтронов (и других
частиц) делится на несколько более
легких ядер
235
92
95
1
U 10 n 139
54 Xe 38 Sr 20 n
реакция синтеза атомных ядер образование из легких ядер более
тяжелых.
63
































 physics
physics








