Методы описания детерминированных и случайных процессов в информационных системах (тема № 4)

1. Теория Информационных Процессов и Систем

Тема №4: Методы описания
детерминированных и случайных
процессов в информационных
системах

2. Содержание

Особенности моделирования случайных
процессов.
События. Случайные величины.
Случайные процессы.
Моделирование случайных процессов.

3. Объекты моделирования

Дискретные
Непрерывные
Детерминированные
• Число состояний
системы конечно.
• Переходы строго
определены
• Число состояний
бесконечно
• Динамика параметров
строго определена
Стохастические
• Число состояний
системы конечно
• Переходы определены
некоторым случайным
законом
• Число состояний
бесконечно
• Динамика параметров
задается случайными
функциями
Вычислительная система – это дискретный детерминированный
объект.
При моделировании решается задача описания любого
объекта дискретной детерминированной
схемой.

4.

Основные вопросы
Дискретизация непрерывной задачи
Сходимость = аппроксимация
+ устойчивость
Оптимизация алгоритма
Описание стохастической задачи как детерминированной
Как вообще вычленить
закономерности в
«случайной» ситуации?
Адекватность: когда и почему
решение детерминированной
задачи «полезно» для
решения стохастической.

5. Содержание

Особенности моделирования случайных
процессов.
События. Случайные величины.
Случайные процессы.
Моделирование случайных процессов.

6. Некоторые определения

7. Некоторые определения

P( A ) 1 полная группа
i
P( Ai Aj ) 0 i j
P( Ai Aj ) P( Ai ) P( Aj ) i j

8. Некоторые определения

X : x1 , x2 ,
xn
в случае полной группы несовместных событий

9. Распределение случайной величины

Дискретная случайная величина
Аналитическое
Табличное
Графическое
Непрерывная случайная величина
Вероятность каждого
конкретного значения
равна нулю - ????

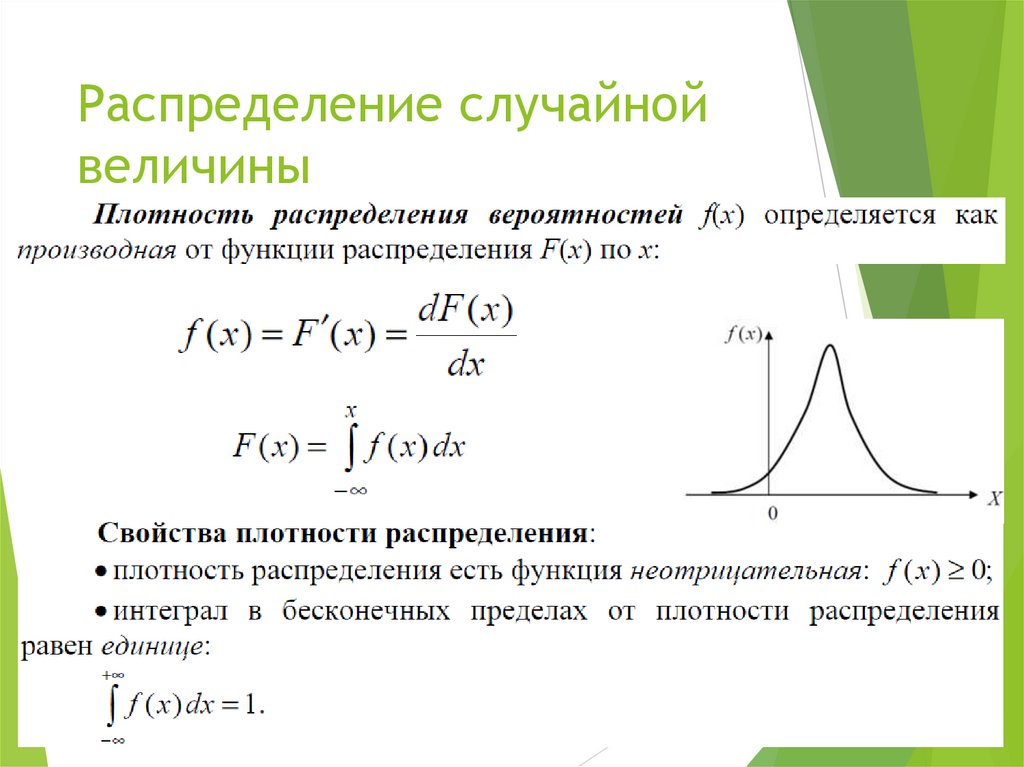
10. Распределение случайной величины

11. Распределение случайной величины

12. Моменты случайной величины

В
Математическое ожидание

13. Моменты случайной величины

Математическое ожидание – средневзвешенное
значение случайной величины
Дисперсия – разброс значений случайной величины
относительно математического ожидания
Среднеквадратичное отклонение
Коэффициент вариации

14. Типовые распределения

Распределение Пуассона
Геометрическое распределение

15. Типовые распределения

Равномерное распределение
Экспоненциальное
распределение
Распределение Эрланга

16. Содержание

Особенности моделирования случайных
процессов.
События. Случайные величины.
Случайные процессы.
Моделирование случайных процессов.

17. Случайный процесс

18. Случайный процесс

19. Случайный процесс

20. Марковские процессы

21. Марковские процессы

22. Марковские процессы

23. Процессы с непрерывным временем

24. Дифференциальная матрица

25. Вектор состояний системы

Состояния системы:
Вероятности нахождения системы в состоянии:
Нормировочное условие:
Стохастический вектор состояний системы:

26. Эргодические процессы

27. Эргодические процессы

28. Эргодические процессы

29. Эргодические процессы

30. Марковские процессы с дискретным временем

Система линейных алгебраических уравнений для расчёта
стационарных вероятностей состояний марковского процесса, которая
обладает единственным решением, если Q – эргодическая матрица.

31. Марковские процессы с непрерывным временем

32. Содержание

Особенности моделирования случайных
процессов.
События. Случайные величины.
Случайные процессы.
Моделирование случайных процессов.

33. Моделирование марковских процессов

34. Моделирование марковских процессов

35. Моделирование марковских процессов

36. Моделирование марковских процессов