Второе начало термодинамики. Энтропия

1. Второе начало термодинамики. Энтропия

2.

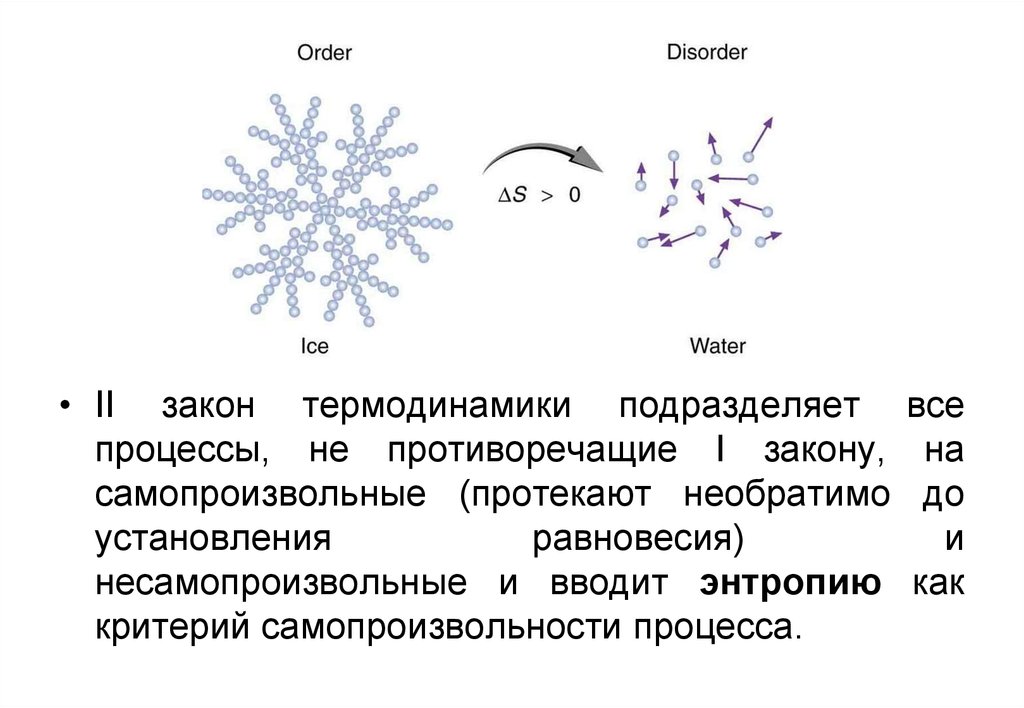
• II закон термодинамики подразделяет
процессы, не противоречащие I закону,
самопроизвольные (протекают необратимо
установления
равновесия)
несамопроизвольные и вводит энтропию
критерий самопроизвольности процесса.
все
на
до
и
как

3.

Вечный двигатель 2-го рода не существует.
Энергия Вселенной постоянна, а её
энтропия возрастает.
Теплота
наиболее
холодного
из
участвующих в процессе тел не может
служить источником работы (постулат
Томсона).
Теплота сама собой не может переходить
от холодного тела к горячему (постулат
Клаузиуса).
Энтропия изолированной системы не
может уменьшаться (Больцман)

4. Существует экстенсивная функция состояния системы – энтропия S, которая возрастает в необратимых процессах и остается неизменной в обрат

Существует экстенсивная функция состояния системы
– энтропия S, которая возрастает в необратимых
процессах и остается неизменной в обратимых.
dS
Q
T
Q
S
T
− дифференциальная форма
(1)
− интегральная форма
(2)
Q/T - приведенная теплота, т.е. теплота, которой система
обменивается с окружающей средой при температуре Т
• Знак равенства имеет место в обратимых, а неравенства
– в необратимых процессах.

5.

dS
Q
T
1) Изолированная система: δQ=0 → dS 0
dS > 0 - процесс протекает самопроизвольно и
необратимо
dS < 0
- процесс и в изолированной системе не
возможен
dS = 0
- состояние термодинамического
равновесия, энтропия достигает
максимальной величины и постоянна

6.

2) Неизолированная система:
Q
- система поглощает тепло из окр.
среды, энтропия системы возрастает
0
T
Q
0
T
- система отдает тепло в окр. среду,
энтропия системы уменьшается
• Энтропия неизолированной системы может возрастать за
счет уменьшения энтропии окружающей среды, поэтому
знак изменения энтропии самой системы не является
критерием самопроизвольности процесса.
dS 0
S S
сис.
можно говорить только о знаке
изменения суммарной энтропии ТДС и
окр. среды, которые не равны по
величине и противоположны по знаку.
-
S
окр .

7. Статистический характер II закона термодинамики

• Не абсолютный закон природы, применим
только к макроскопическим системам.
• Энтропия – мера беспорядка. Для ТДС с
малым
числом
частиц
понятие
«беспорядок» не имеет смысла.
• Для ТДС с малым числом частиц теряют
смысл Р и Т, исчезает различие между
теплотой и работой.

8. Вероятностный характер II закона термодинамики.

• В необратимом самопроизвольном процессе
система переходит от порядка к беспорядку, из
менее вероятного состояния в более вероятное,
что сопровождается ростом энтропии ТДС.
Рост энтропии = рост беспорядка!
• Энтропия характеризует вероятность реализации
данного состояния системы.
S = KlnW - формула Больцмана

9. S = KlnW

W – термодинамическая вероятность (число
способов, которыми можно осуществить данное
состояние системы) ;
K = R/NA – постоянная Больцмана.
W = W 1 • W2 • W3 • … • W i
безразмерная (W ≥ 1)
S = Σ KlnWi = Σ Si
Дж/(моль • К)
- мультипликативная и
- величина аддитивная,

10.

11. Расчет изменения энтропии в различных процессах

dS
1) T=const
Q dU PdV
Q
T
(2)
dU PdV
dS
T
dU T 0 ,
(3)
nRT
P
V
(4)
dV
dS nR
nRd ln V
V
2
2
1
1
(1)
(5)
dS nR d ln V
V2
P1
S nR ln
nR ln
,
V1
P2
P1V1 P2V2
(6)

12.

dS
2) V=const
Q
dU CV dT
dS V
T
T
T
dU CV dT
2
2
dS
1
а) СV=const
S CV ln
S
1
C P dT
1 T
2
а) СР=const
T2
T1
S C P ln
б) СV, СР= f (T) ,
2
T
3) P=const
Q
dH C P dT
dS P
T
T
T
dH C P dT
CV dT
dS
1
1 T
2
Q
a bT cT
2
T
c T 2 dT
T2
T1
C = a + bT + cT2 + c T-2
T2
c 2
c 1
1
2
a ln b T2 T1 T2 T1 2 2
T1
2
2 T2 T 1

13.

4) при фазовых переходах вещества
(Т, Р)ФП = const
dSФП
QP
TФП
dHФП
TФП
SФ. П .
H Ф. П .
TФ. П .
∆Hф.п. и Tф.п. – теплота и температура фазового перехода
5) расчет изменения энтропии в химической реакции
CP0 a bT cT 2 c T 2
S S
0
T
0
298
T
c 2
c 1
1
2
a ln
b T 298
T 298
2
2
298
2
2 T
298

14. Постулат Планка (третий закон термодинамики)

Абсолютная энтропия

15.

Вблизи температуры абсолютного нуля (Т=0 К) все
вещества находятся в состоянии идеального кристалла
и имеют энтропию, равную нулю:
lim S T 0 0
S T0 - абсолютная энтропия вещества при температуре Т,
0
S 298 - абсолютная энтропия вещества в стандартных условиях.
Абсолютные энтропии рассчитывают интегрированием II
закона термодинамики при Р=const.
а) в отсутствие фазовых превращений
интервале температур от 0 до Т, К
Т
Т
CP dT
dS T
0
0
Т
вещества
C P dT
ST
T
0
0
на

16. б) при наличии фазовых превращений вещества на интервале от 0 до Т, К

б) при наличии фазовых
интервале от 0 до Т, К
ST0
Т пл
0
превращений
вещества
на
Т
CРТВ dT ПЛ Ткип СРЖ dT ИСП
СРГ dT
T
Т ПЛ
T
Т КИП
T
Т кип
Т пл

17. Следствия из постулата Планка

При равенстве энтропии нулю равны нулю и все её первые
производные по параметрам состояния системы:
S
S
0
V T 0 P T 0
Вблизи Т=0 К теплоемкость веществ в твердом состоянии
также стремится к нулю
Т
C P dT
ST
0 CP 0
T
0
0
Тепловая теорема Нернста (постулат о касательной)
Вблизи Т=0 К реакции между веществами в конденсированном
состоянии протекают без изменения энтропии
G T S
T 0 G

18. Постулат о касательной

Вблизи
температуры
абсолютного «0» для реакций
между
веществами
в
конденсированном состоянии
кривые зависимостей ΔG=f(T)
и ΔH=f(T)
асимптотически
сближаются и имеют общую
касательную в точке Т=0.
G
lim
lim
0
T 0
T P T 0 T P
G
S 0 ,
T P
CP 0
T P