Similar presentations:
Конечные и бесконечные множества
1.
Конечные и бесконечныемножества
2.
Мощность множестваКоличество элементов множества A называется мощностью
множества А и обозначается │А│ или n(A).
А – некоторое множество
n(A) – количество элементов множества А (его
мощность)
• А – множество дней недели
n(A)=7
• А множетво двузначных чисел
n(A)=90
3.
Количество подмножествЕсли мощность множества n, то у этого множества 2n подмножеств.
Пример1:
А={1,2}, n(A)=2, 22 = 4
Подмножества множества А:
{ }, {1}, {2}, {1,2}.
Пример2:
А={1,2,3} , n(A)=3, 23 = 8
Подмножества множества А:
{ }, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}
4.
5.
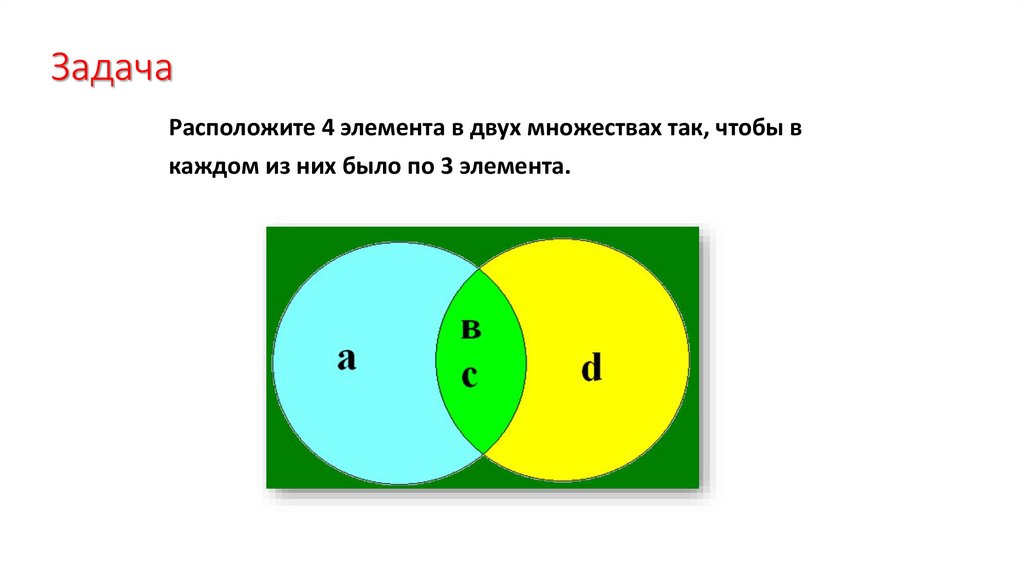
ЗадачаРасположите 4 элемента в двух множествах так, чтобы в
каждом из них было по 3 элемента.
6.
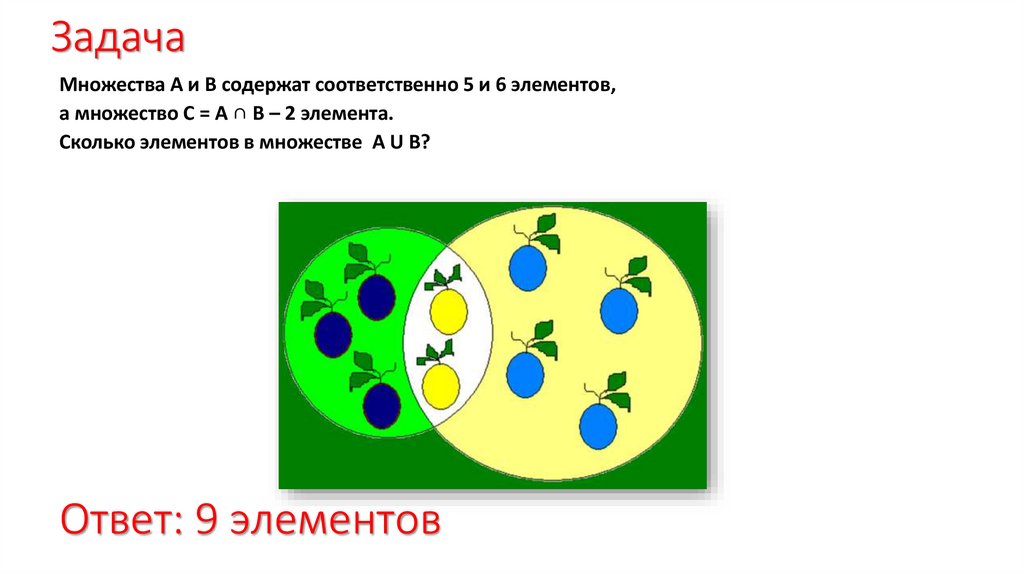
ЗадачаМножества А и В содержат соответственно 5 и 6 элементов,
а множество С = А ∩ В – 2 элемента.
Сколько элементов в множестве А U В?
Ответ: 9 элементов
7.
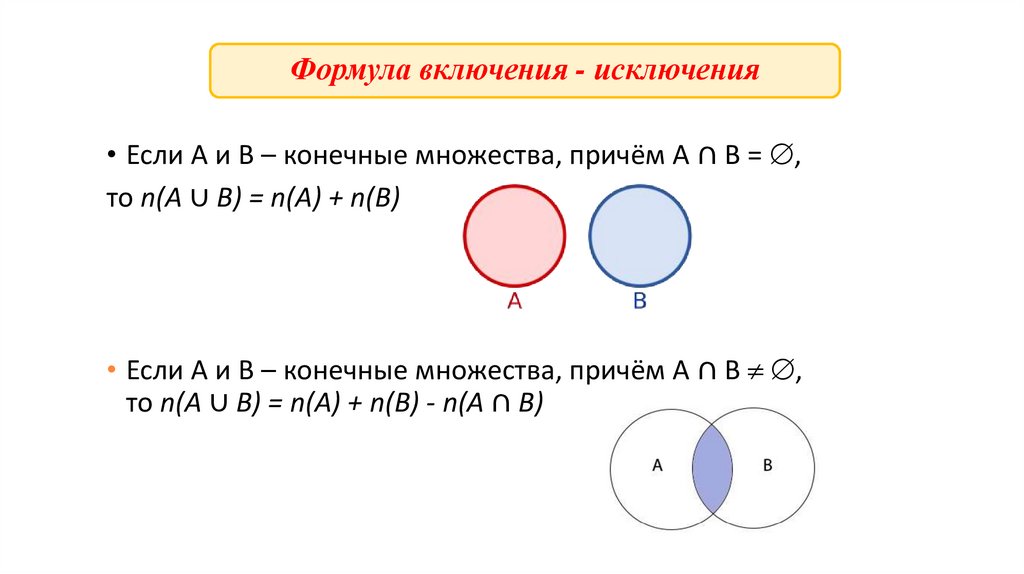
Формула включения - исключения• Если А и В – конечные множества, причём А ∩ В = ,
то n(А ∪ В) = n(А) + n(В)
• Если А и В – конечные множества, причём А ∩ В ,
то n(А ∪ В) = n(А) + n(В) - n(А ∩ В)
8.
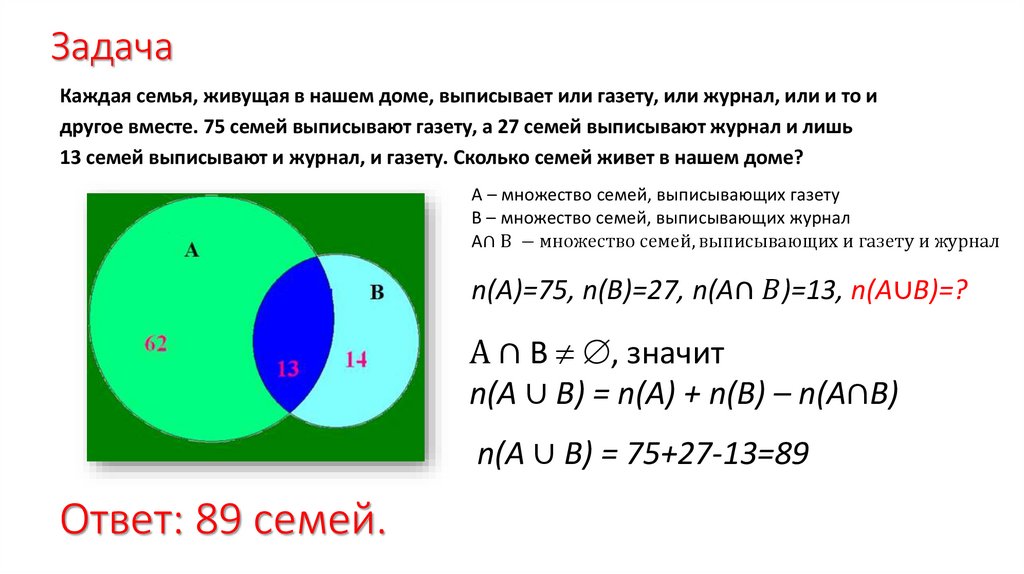
ЗадачаКаждая семья, живущая в нашем доме, выписывает или газету, или журнал, или и то и
другое вместе. 75 семей выписывают газету, а 27 семей выписывают журнал и лишь
13 семей выписывают и журнал, и газету. Сколько семей живет в нашем доме?
А – множество семей, выписывающих газету
В – множество семей, выписывающих журнал
А∩ В − множество семей, выписывающих и газету и журнал
n(А)=75, n(B)=27, n(A∩





 mathematics
mathematics








