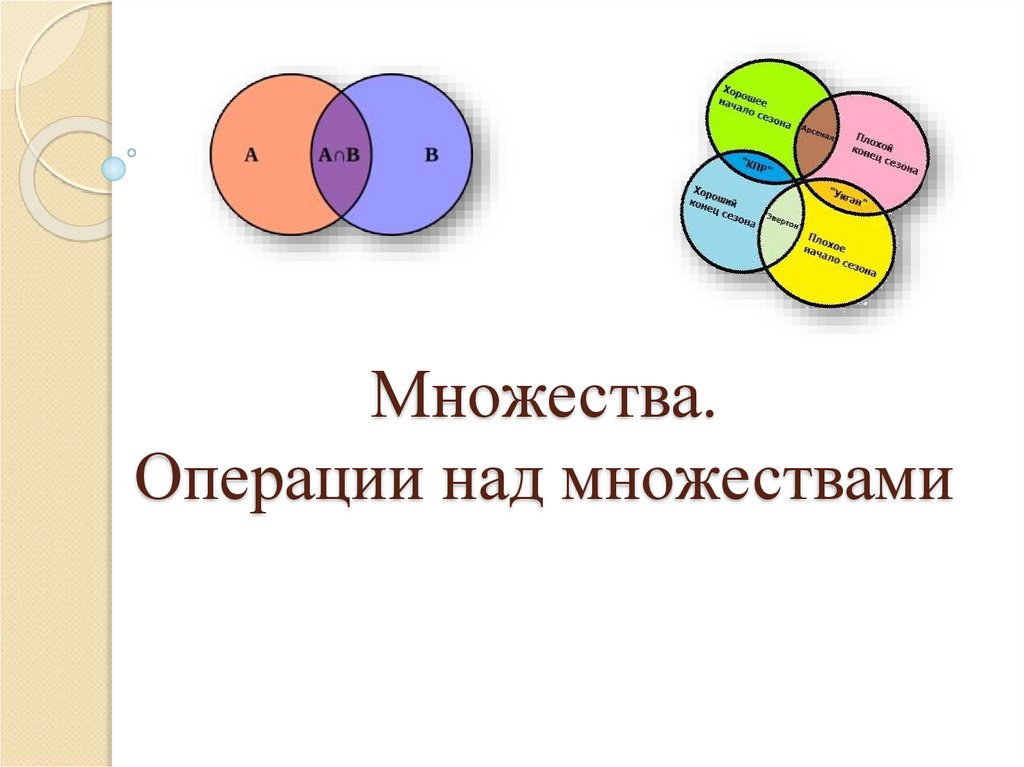
Множества. Операции над множествами

1. Множества. Операции над множествами

2.

«Множество есть многое, мыслимое
нами как единое»
основатель теории множеств – Георг Кантор
(1845—1918) — немецкий
математик, логик, теолог, создатель
теории бесконечных множеств,
оказавшей определяющее влияние
на развитие математических наук на
рубеже 19— 20 вв.

3. Примеры множеств из окружающего мира

Например, множество дней
недели состоит из элементов:
понедельник, вторник, среда,
четверг, пятница, суббота,
воскресенье.
Множество месяцев – из
элементов: январь, февраль,
март, апрель, май, июнь, июль,
август, сентябрь, октябрь,
ноябрь, декабрь.

4.

Придумай название для предметов и животных,
собранных вместе:
НАБОР
КОЛЛЕКЦИЯ МАРОК КАРАНДАШЕЙ
ЧАЙНЫЙ СЕРВИЗ
БУКЕТ ЦВЕТОВ
СТАЯ ПТИЦ
СТАДО КОРОВ

5. Примерами множеств в геометрии могут служить:

а) множество видов треугольников,
б) множество многоугольников

6.

Множество – совокупность объектов,
объединенных по какому – нибудь признаку.
Множества обозначают большими буквами
латинского алфавита: А, В, С, D и т. д.
Объекты, составляющие множество,
называются элементами множества.

7.

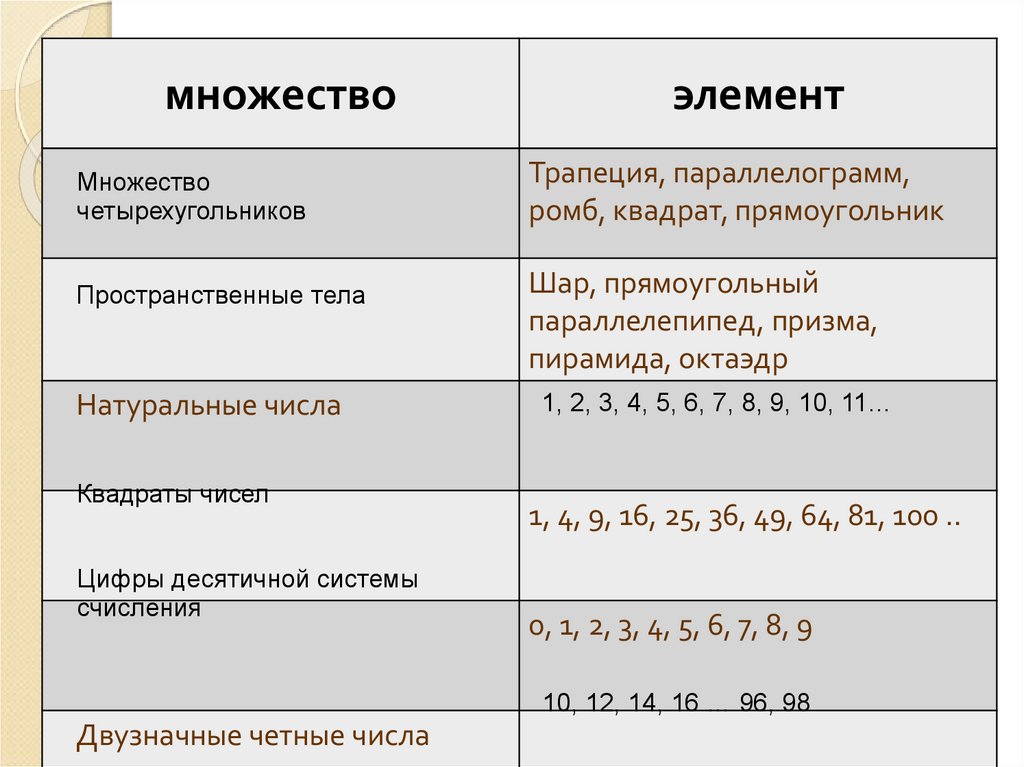
множество
элемент
Множество
четырехугольников
Трапеция, параллелограмм,
ромб, квадрат, прямоугольник
Пространственные тела
Шар, прямоугольный
параллелепипед, призма,
пирамида, октаэдр
Натуральные числа
Квадраты чисел
Цифры десятичной системы
счисления
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…
1, 4, 9, 16, 25, 36, 49, 64, 81, 100 ..
0, 1, 2, 3, 4, 5, 6, 7, 8, 9
10, 12, 14, 16 … 96, 98
Двузначные четные числа

8.

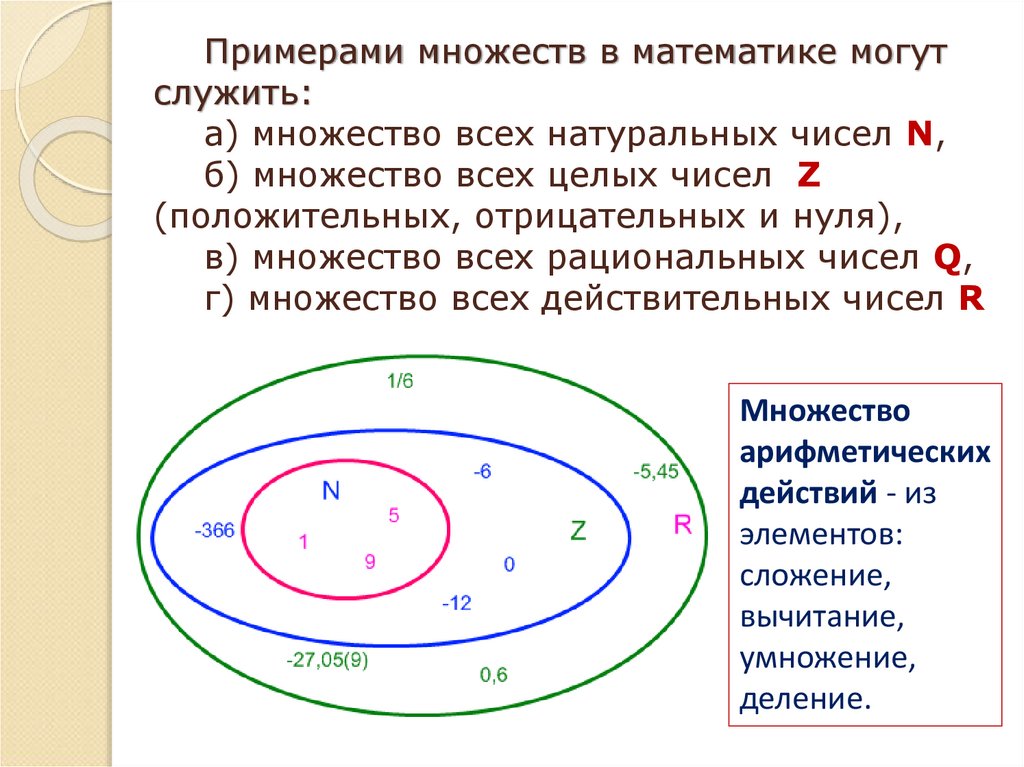
Примерами множеств в математике могут
служить:
а) множество всех натуральных чисел N,
б) множество всех целых чисел Z
(положительных, отрицательных и нуля),
в) множество всех рациональных чисел Q,
г) множество всех действительных чисел R
Множество
арифметических
действий - из
элементов:
сложение,
вычитание,
умножение,
деление.

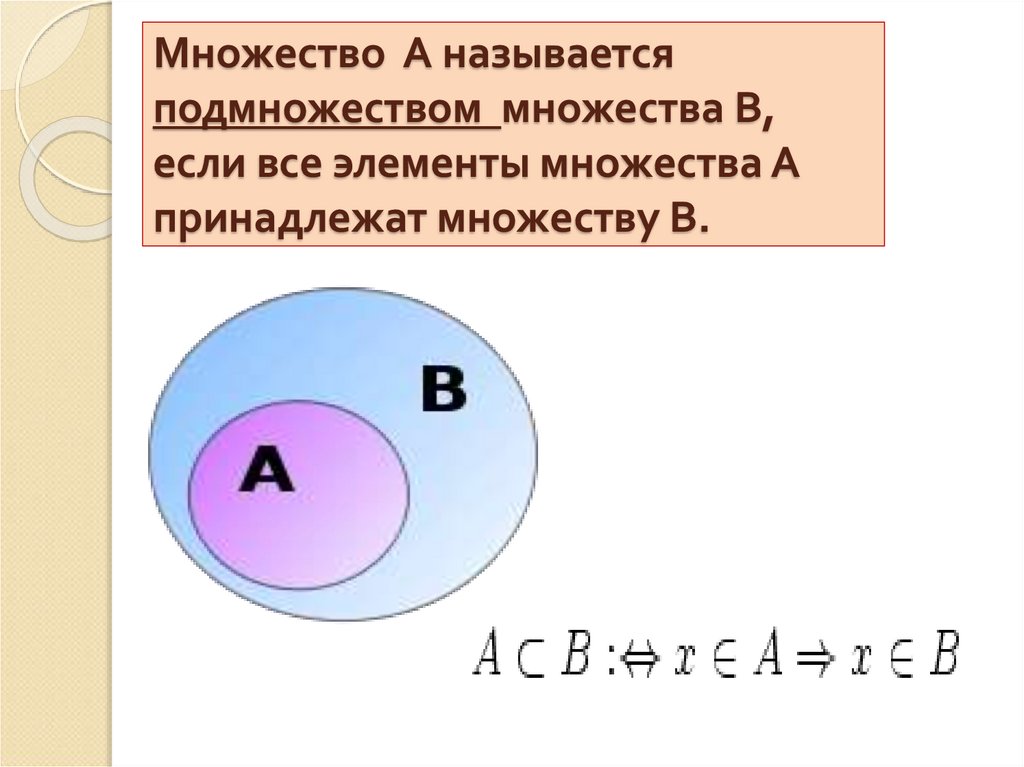
9. Множество А называется подмножеством множества В, если все элементы множества А принадлежат множеству В.

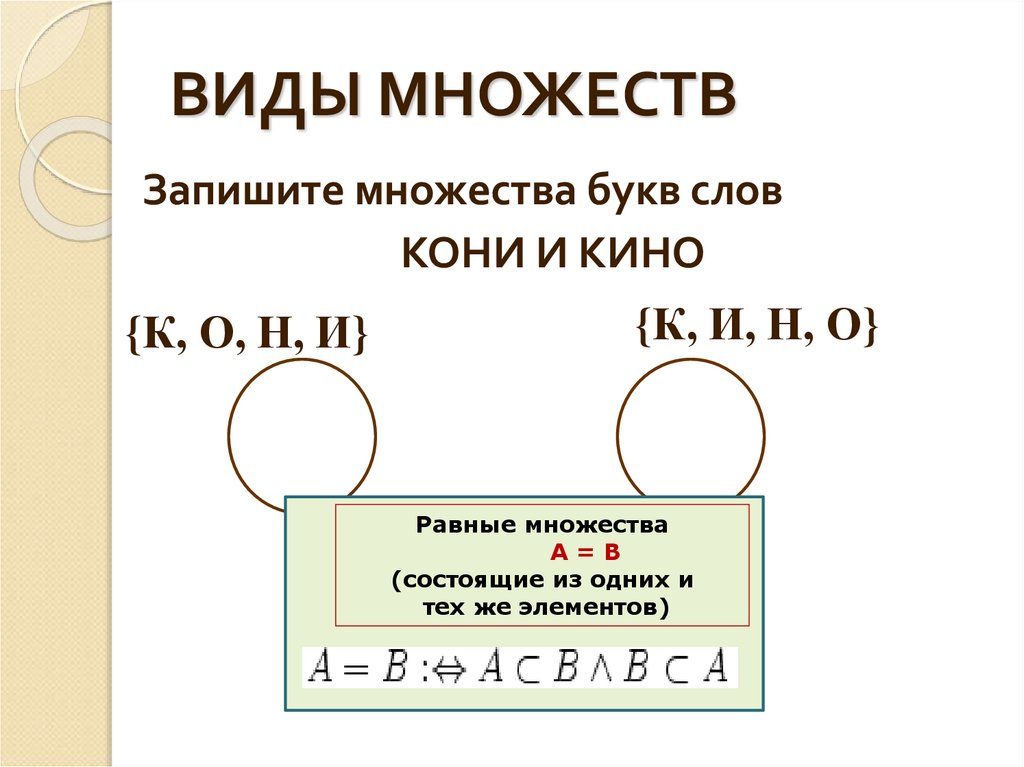
10. ВИДЫ МНОЖЕСТВ

Запишите множества букв слов
КОНИ И КИНО
{К, О, Н, И}
{К, И, Н, О}
Равные множества
А=В
(состоящие из одних и
тех же элементов)

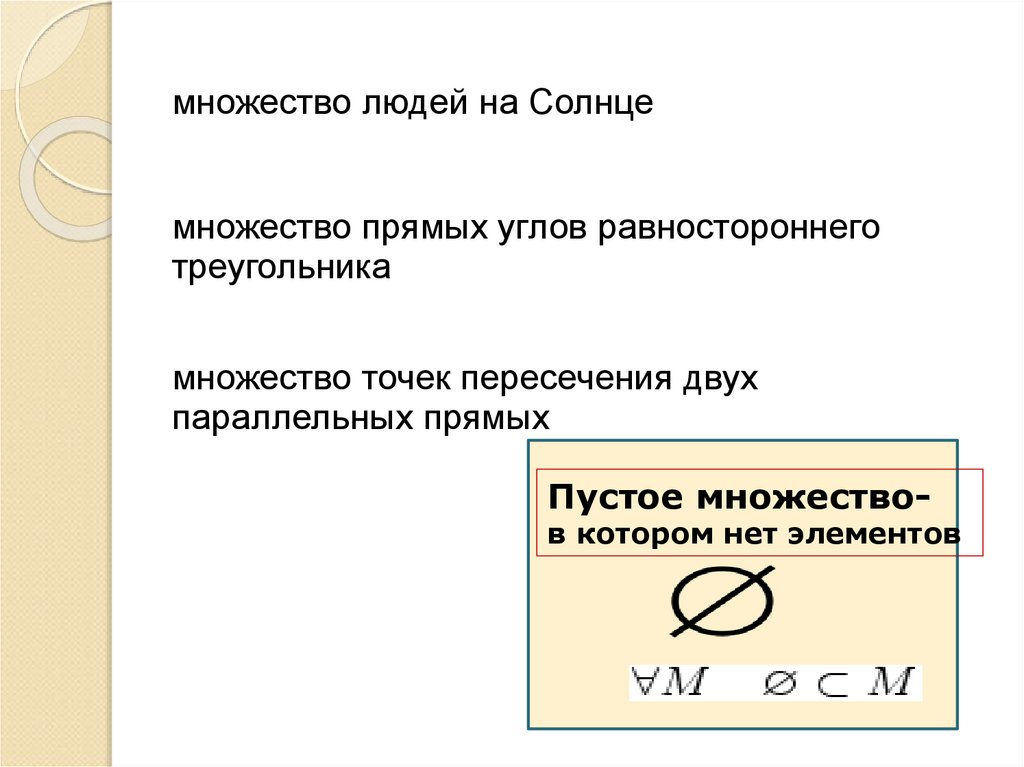
11.

множество людей на Солнце
множество прямых углов равностороннего
треугольника
множество точек пересечения двух
параллельных прямых
Пустое множество-
в котором нет элементов

12. ВИДЫ МНОЖЕСТВ

А = {2; 3; 5; 7; 11; 13};
{х | 5< х <12}
Конечные множества

13. ВИДЫ МНОЖЕСТВ

{1; 4; 9; 16; 25; …};
{10; 20; 30; 40; 50; …};
Бесконечные множества

14.

Среди перечисленных ниже множеств укажите
конечные и бесконечные множества:
а) множество чисел, кратных 13;
б) множество делителей числа 15;
в) множество деревьев в лесу;
г) множество натуральных чисел;
д) множество рек Ростовской области;
е) множество корней уравнения х + 3 = 11;
ж) множество решений неравенства х + 1 < 3.

15.

16.

17.

18. ДЕЙСТВИЯ НАД МНОЖЕСТВАМИ

19.

Пересечением двух множеств А и В называется
множество С = А В, которое состоит из всех
элементов х, лежащих одновременно в
множестве А и в множестве В.
А В = {х}, где х А и х В
М= а
с

20.

ЗАДАЧА 1
А
ЗАДАЧА 2

21.

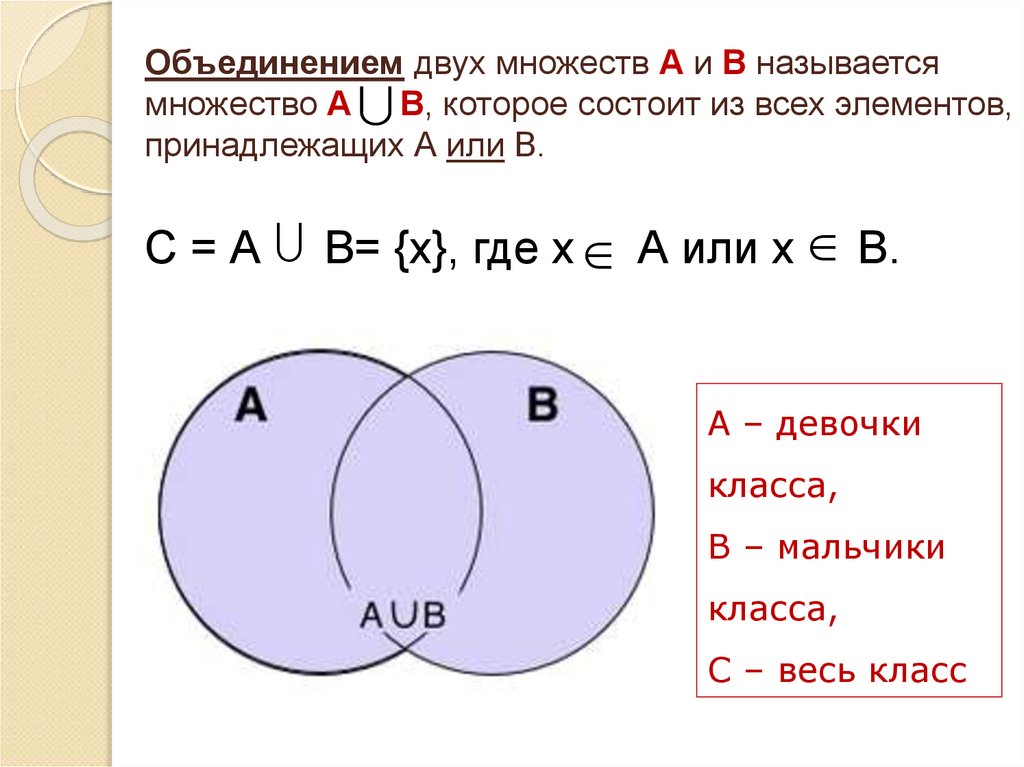
Объединением двух множеств А и В называется
множество А В, которое состоит из всех элементов,
принадлежащих А или В.
С = А В= {х}, где х А или х В.
А – девочки
класса,
В – мальчики
класса,
С – весь класс

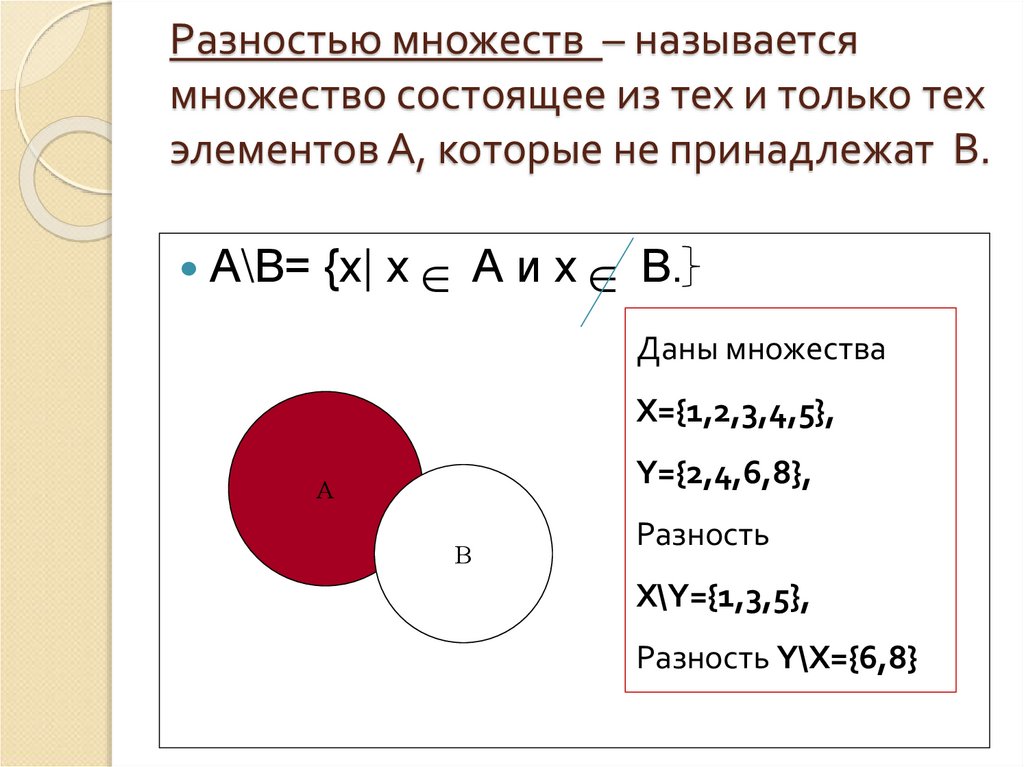
22. Разностью множеств – называется множество состоящее из тех и только тех элементов А, которые не принадлежат В.

А\В= {х| х А и х В.
Даны множества
X={1,2,3,4,5},
Y={2,4,6,8},
А
В
Разность
X\Y={1,3,5},
Разность Y\X={6,8}

23. Дополнение к множеству -элементы, которые не принадлежат множеству А (т.е. дополняют его до универсального)

Предположим, что
множество U состоит из всех
букв русского алфавита,
U
Аа
В
А
А
A – из всех согласных
Тогда:
дополнение множества А
до универсального
множества U – из всех
гласных.

24.

№1
Какое множество задано путем
перечисления данных элементов?
А={0,1,2,3,4,5,6,7,8,9}
В={А,Е,И,О,У,Э,Ю,Я}
№2
№3
Задайте
множество крокодилов, летящих в
небе.
Даны множества
А = {3, 5, 0, 11, 12, 19},
В = {2, 4, 8, 12, 18,0}. Найдите множества
AUВ,
А В

25.

Решение задачи
с помощью кругов Эйлера
k
K
́ д Э́йлер —
Леонар
швейцарский, немецкий и
российский математик,
внёсший значительный вклад в
развитие математики, а также
механики, физики, астрономии
и ряда прикладных наук.

26.

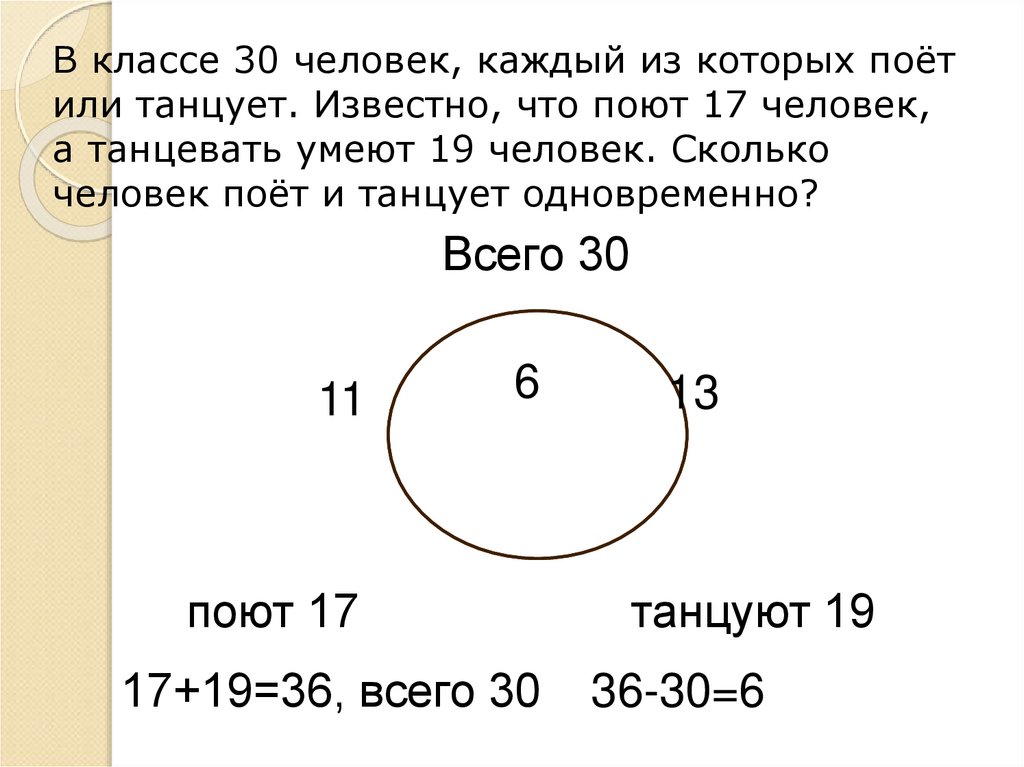
В классе 30 человек, каждый из которых поёт
или танцует. Известно, что поют 17 человек,
а танцевать умеют 19 человек. Сколько
человек поёт и танцует одновременно?
Всего 30
11
6
поют 17
17+19=36, всего 30
13
танцуют 19
36-30=6

27. Решение

Пусть А - это множество учеников, умеющих петь.
Количество элементов в нём по условию равно n = 17.
Пусть В - множество учеников, умеющих танцевать.
Количество элементов в нём - m = 18. Множество
совпадает со всем классом, т.к. каждый ученик в
классе поёт или танцует. А В - это множество тех
учеников класса, которые поют и танцуют
одновременно. Пусть их количество равно k.
Согласно формуле доказанной выше
n + m- k = 17+ 19- k = 30 k = 6.
Ответ: 6 учеников в классе поют и танцуют
одновременно.

28.

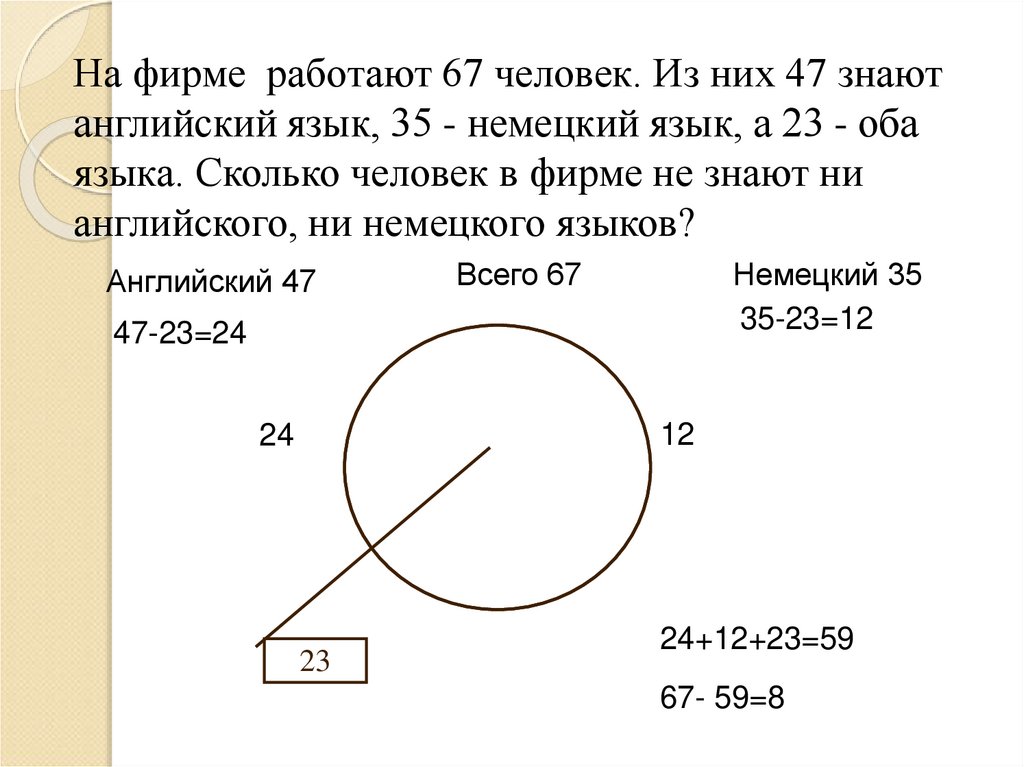
На фирме работают 67 человек. Из них 47 знают
английский язык, 35 - немецкий язык, а 23 - оба
языка. Сколько человек в фирме не знают ни
английского, ни немецкого языков?
Английский 47
Всего 67
Немецкий 35
35-23=12
47-23=24
12
24
23
24+12+23=59
67- 59=8

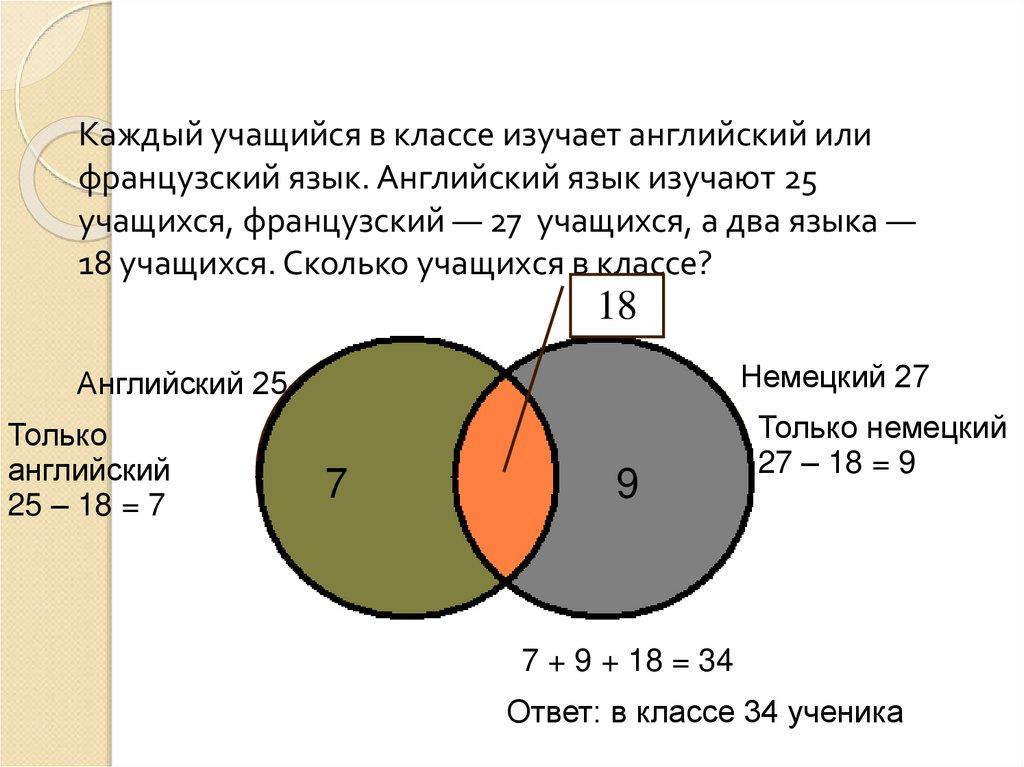
29. Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27

учащихся, а два языка —
18 учащихся. Сколько учащихся в классе?
18
Немецкий 27
Английский 25
Только
английский
25 – 18 = 7
7
9
Только немецкий
27 – 18 = 9
7 + 9 + 18 = 34
Ответ: в классе 34 ученика

30.

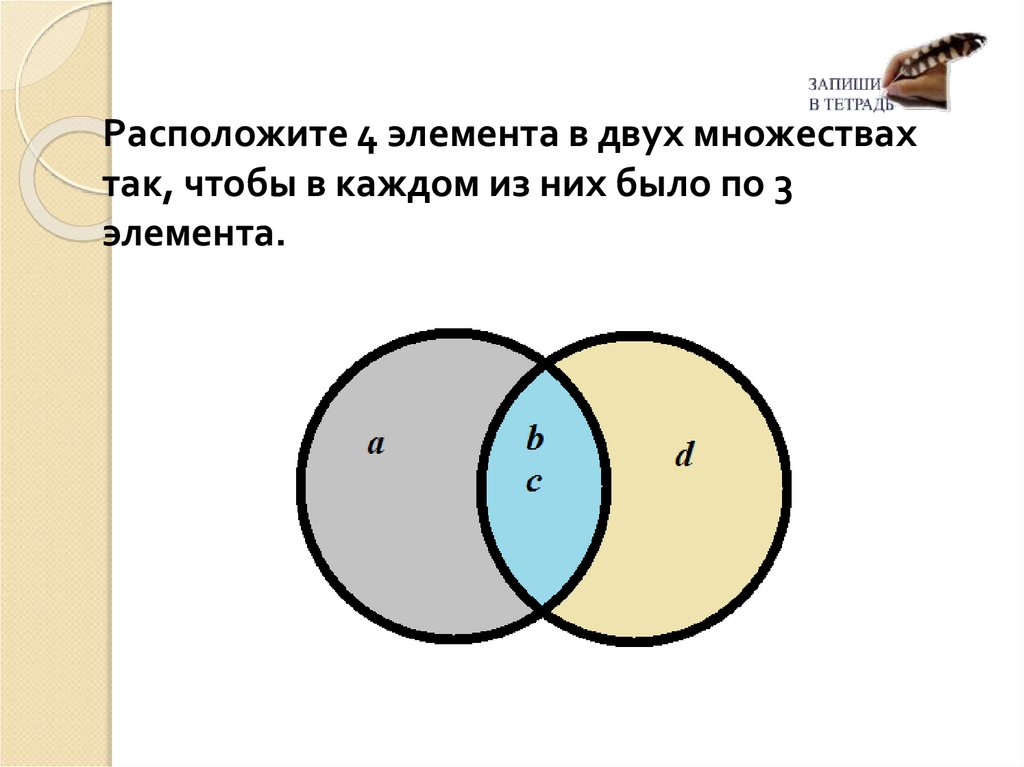
Расположите 4 элемента в двух множествах
так, чтобы в каждом из них было по 3
элемента.

31.

Множества А и В содержат соответственно 5 и 6
элементов, а множество А ∩ В – 2 элемента. Сколько
элементов в множестве А U В?
Объединение содержит 9 элементов

32.

Каждая семья, живущая в нашем доме, выписывает или
газету, или журнал, или и то и другое вместе. 75 семей
выписывают газету, а 27 семей выписывают журнал и
лишь 13 семей выписывают и журнал, и газету. Сколько
семей живет в нашем доме?
Всего: 14 + 13 + 62 =89
32

33.

МНОЖЕСТВО
ЭЛЕМЕНТ МНОЖЕСТВА
ВИДЫ МНОЖЕСТВ
ОТНОШЕНИЯ МЕЖДУ
МНОЖЕСТВАМИ
ОБЪЕДИНЕНИЕ МНОЖЕСТВ
ПЕРЕСЕЧЕНИЕ МНОЖЕСТВ
НАХОДИТЬ
ОБЪЕДИНЕНИЕ
МНОЖЕСТВ
НАХОДИТЬ
ПЕРЕСЕЧЕНИЕ
МНОЖЕСТВ
ИЗОБРАЖАТЬ С
ПОМОЩЬЮ КРУГОВ
ЭЙЛЕРА-ВЕННА
РЕШАТЬ ЗАДАЧИ С
ИСПОЛЬЗОВАНИЕМ
ИМЕЮЩИХСЯ ЗНАНИЙ