Similar presentations:
Математическая логика (ИТ). Тема 2. Логика высказываний
1. МАТЕМАТИЧЕСКАЯ ЛОГИКА (ИТ)
12.
•Тема 2:Логикавысказываний
2
3.
Лекция 43
4.
•Функциональнаяполнота
систем логических
функций
4
5. С.94-145
6. С.47-145
7.
Логические функции однойи двух переменных
называются
элементарными
В В
В В
2
где В – бинарное
множество {0,1}
7
8.
1. Логическиефункции одной
переменной
9.
•Сколько всегофункций
одной
переменной?
10.
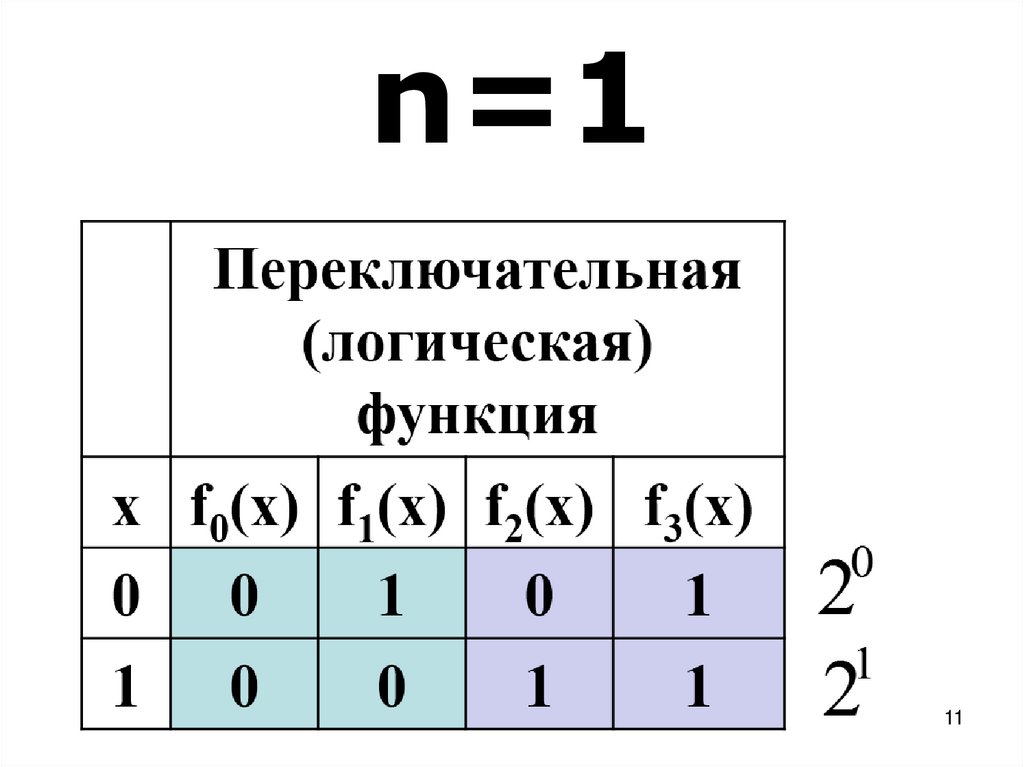
2 211. n=1
1112.
2.Логическиефункции двух
переменных
13.
•Сколько всегофункций двух
переменных?
14.
2 2 2 215.
•Сколько всегофункций n
переменных?
16.
2n
2
16
17.
1718.
1819.
1920.
2021.
3.Суперпозицияи проблема
функциональной
полноты
22. Суперпозиция
•Подстановка вданную функцию
вместо ее
переменных
других функций.
22
23. Проблема функциональной полноты
• Каким должен бытьминимальный состав
элементарных логических
функций, чтобы путём
суперпозиции получить любую
сколь угодно сложную
логическую функцию от
конечного числа переменных?
23
24.
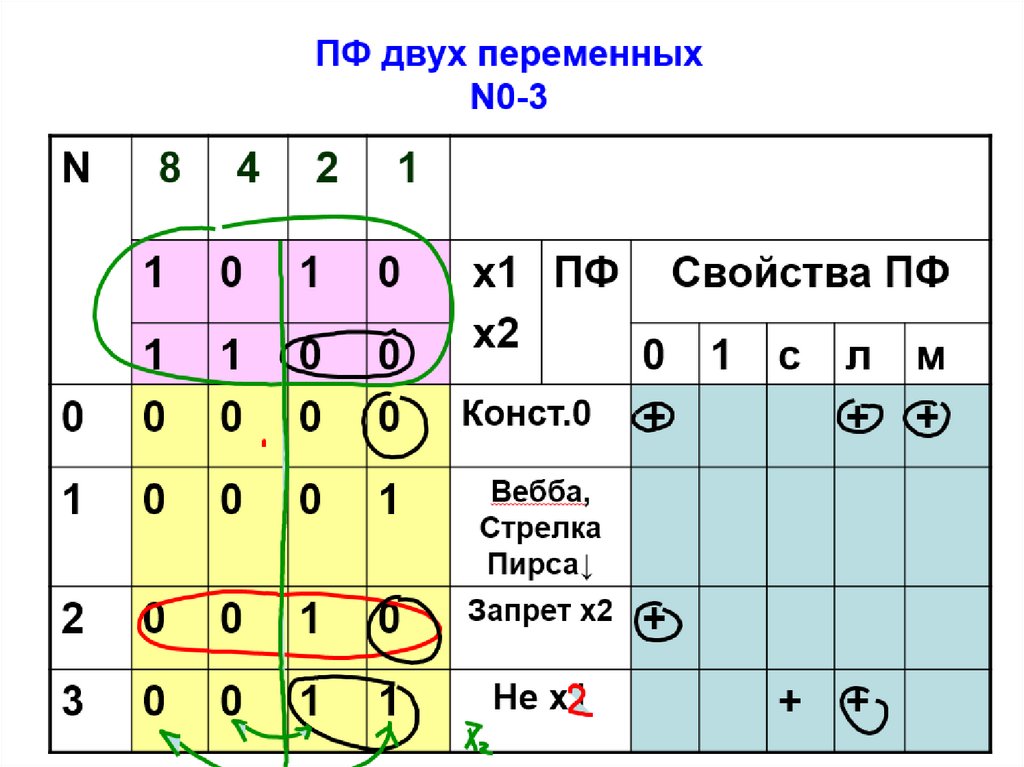
•Классы ПФ25.
•1) класс функций,сохраняющих
константу 0.
•В этот класс входят
функции, которые на
нулевом наборе
переменных
принимают нулевое
значение: f(00...0)=0.
25
26.
•2) класс функций,сохраняющих
константу 1.
•В этот класс входят
функции, которые на
единичном наборе
переменных
принимают единичное
значение: f(11...1)=1.
26
27.
2728.
2829.
2930.
3031.
Самодвойственность32. Двойственность f и g
f ( x1 x2 ....xn ) g(x1 x 2 ...x n )x1 x 2 x1 x 2
33. Двойственность f и g
f ( x1 x2 ....xn ) g(x1 x 2 ...x n )x1 x 2 x 1 x 2
34.
•Самодвойственностьf(x 1x 2 ....x n ) f ( x1 x 2 ...x n )
35.
3536.
3637.
3738.
3839.
•Линейность40. Класс линейных функций.
• функция называется линейной,если возможно представление
в виде линейного полинома,
использующего функцию
сложения по модулю 2:
f(x1x2)=с0 с1х1 с2х2,
где с0,с1,с2 – константы 0, 1.
41. f(x1x2)=с0с1х1с2х2
f(x1x2)=с0 с1х1 с2х241
42.
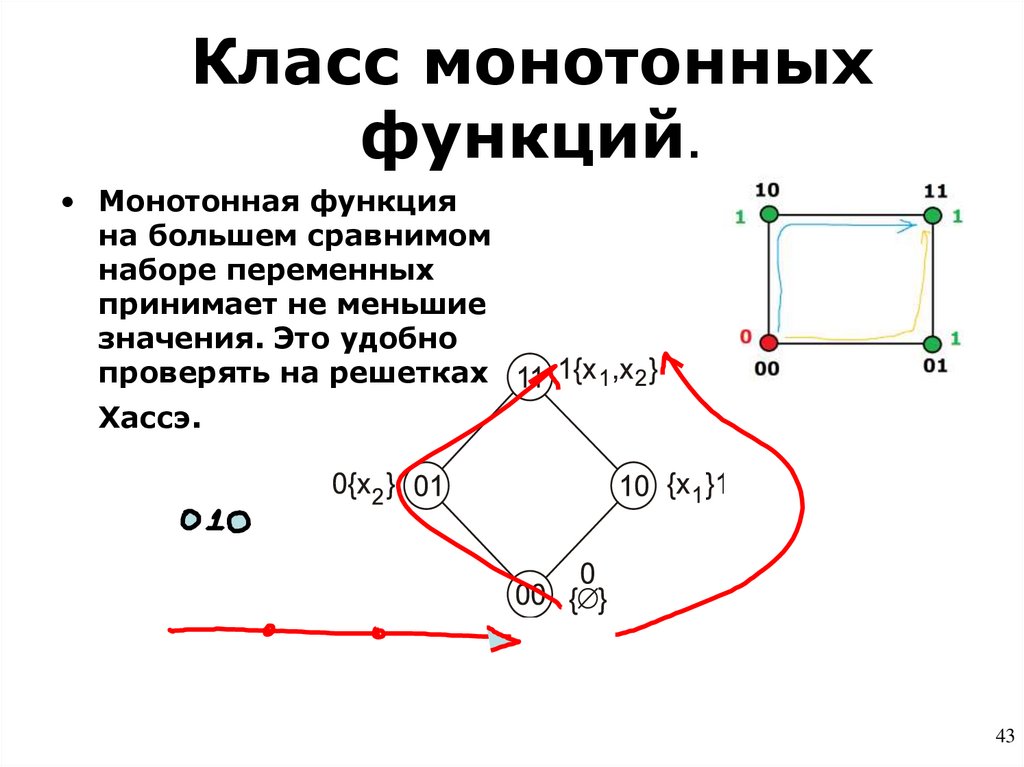
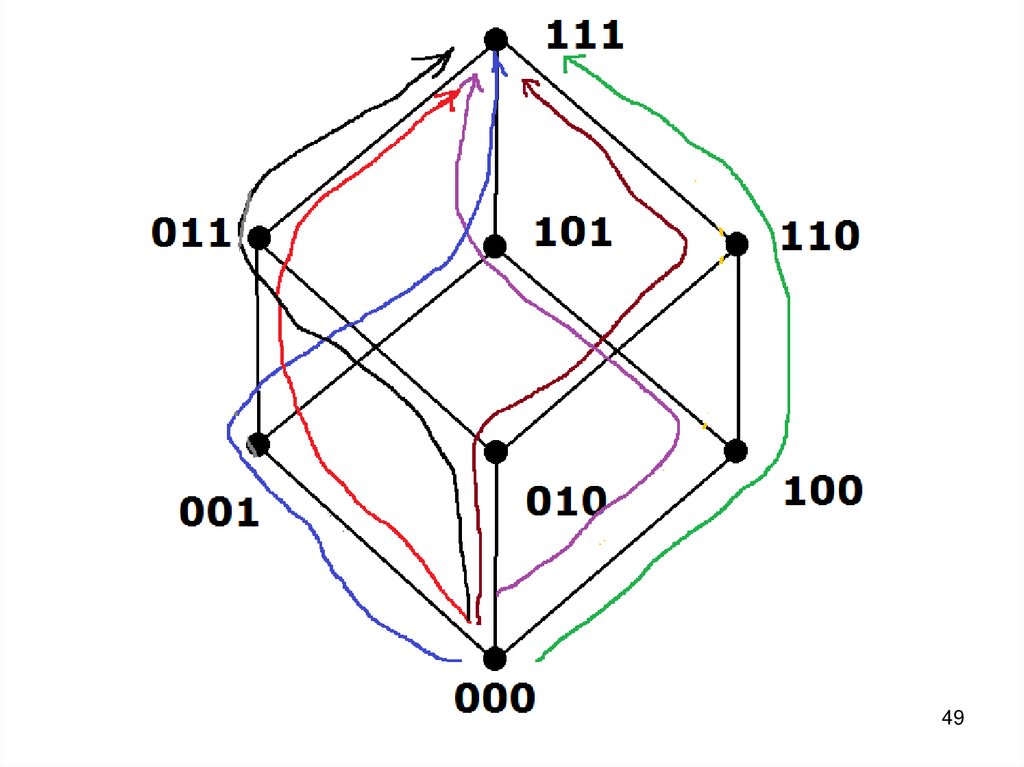
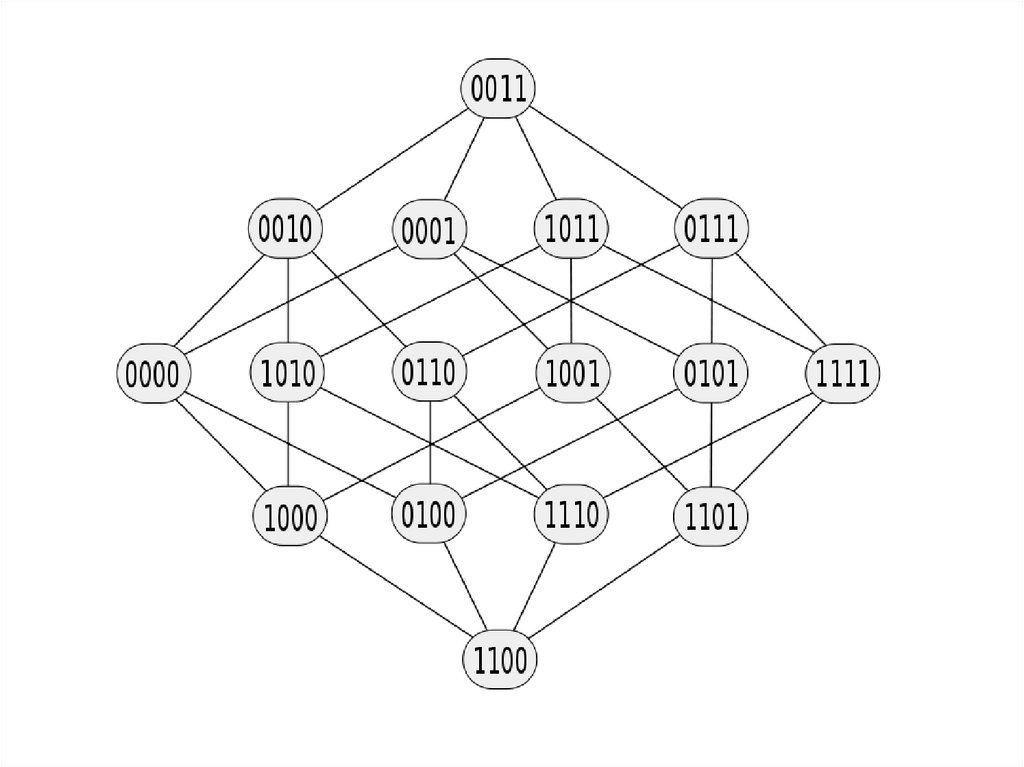
•Монотонность43. Класс монотонных функций.
• Монотонная функцияна большем сравнимом
наборе переменных
принимает не меньшие
значения. Это удобно
проверять на решетках
Хассэ.
43
44.
4445.
4546.
4647.
4748.
4849.
4950.
51.
•3.Теорема(критерий) Поста
52.
Пост, Эмиль Леон (1897 – 1954)53.
• Система функцийназывается функционально
полной, если любая
произвольная
переключательная функция
от любого числа
переменных может быть
представлена в виде
суперпозиции логических
функций из этой системы.
54.
• для функциональной полнотысистем логических функций
необходимо и достаточно,
чтобы они содержали
следующие функции:
• не сохраняющую константу 0;
• не сохраняющую константу 1;
• не самодвойственную;
• не линейную;
• не монотонную.
54
55.
• Функционально полныесистемы
переключательных
функций представляют
собой базис.
• Всего можно получить 17
различных минимальных
базисов из логических
функций двух
переменных.
55
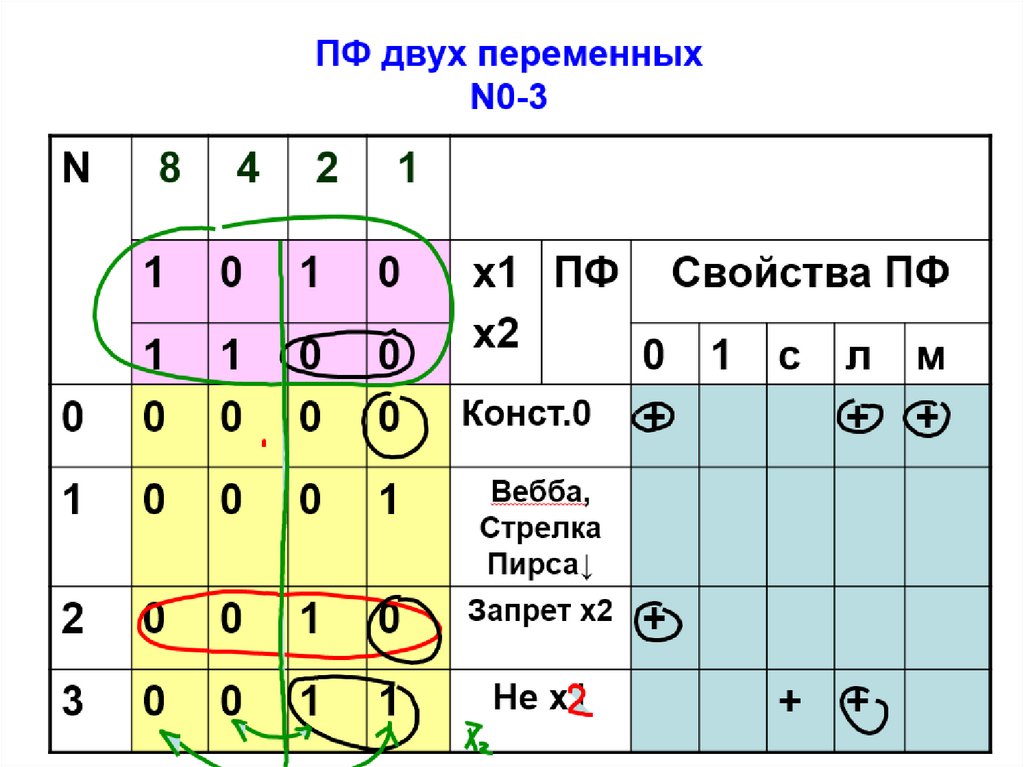
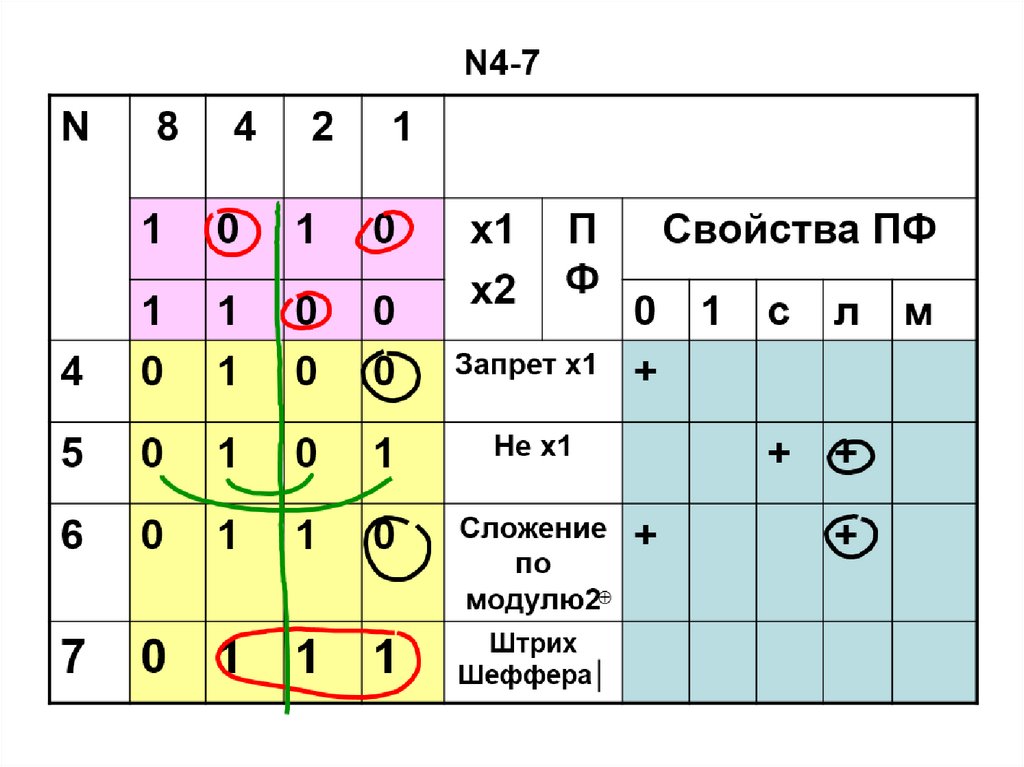
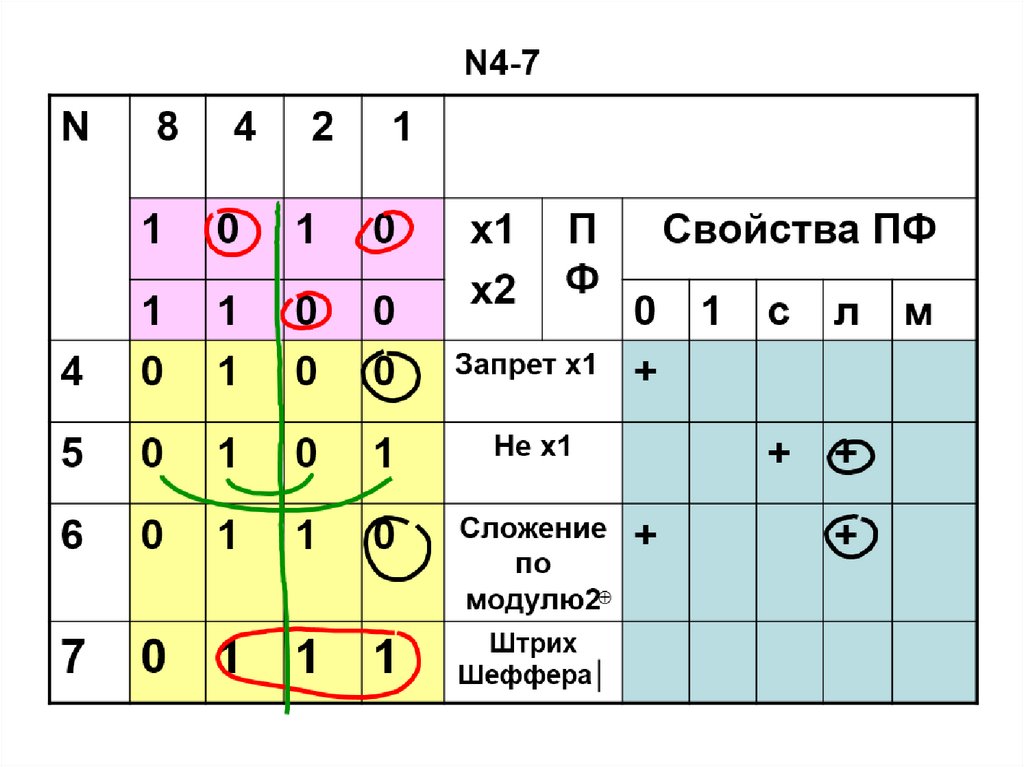
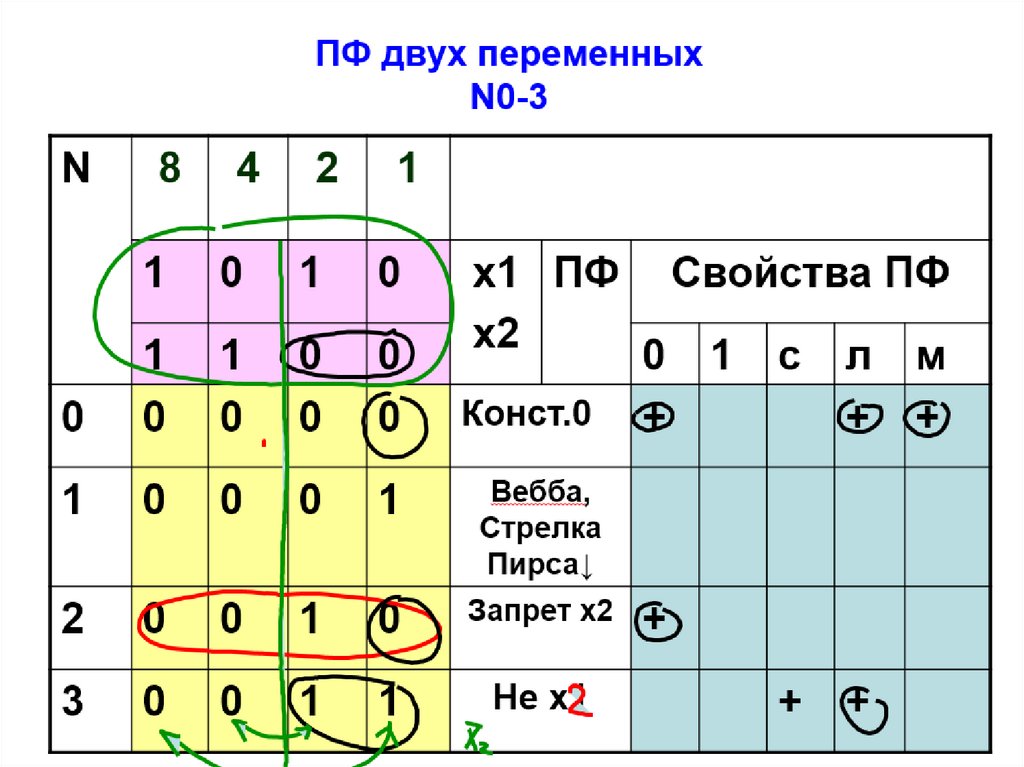
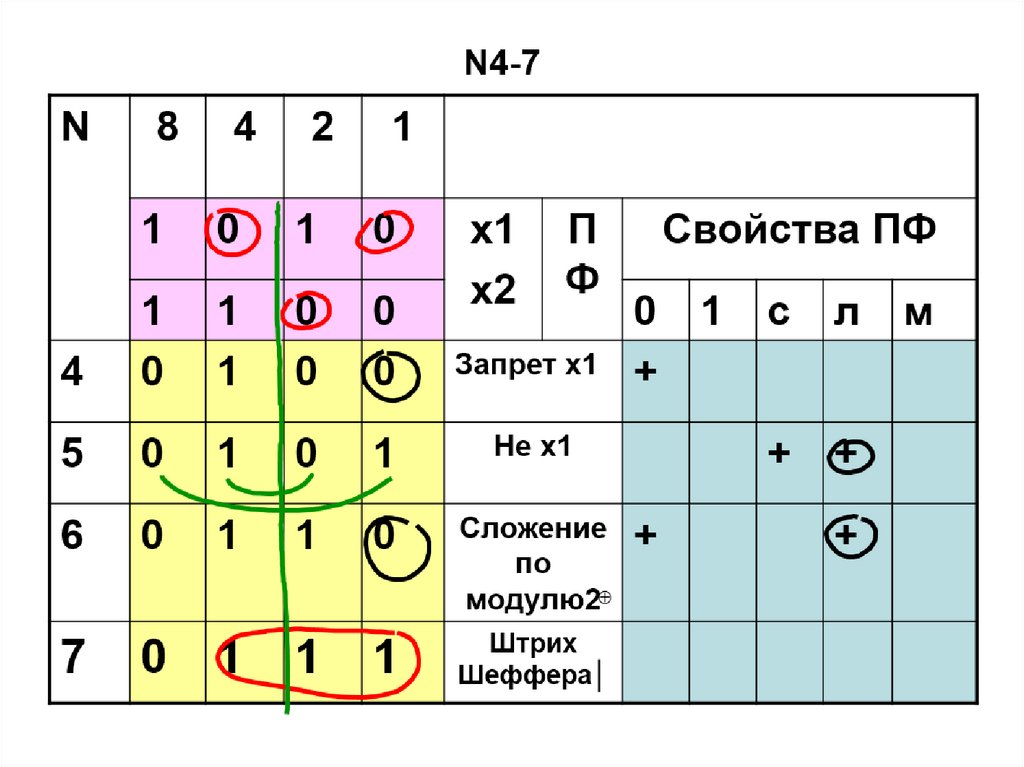
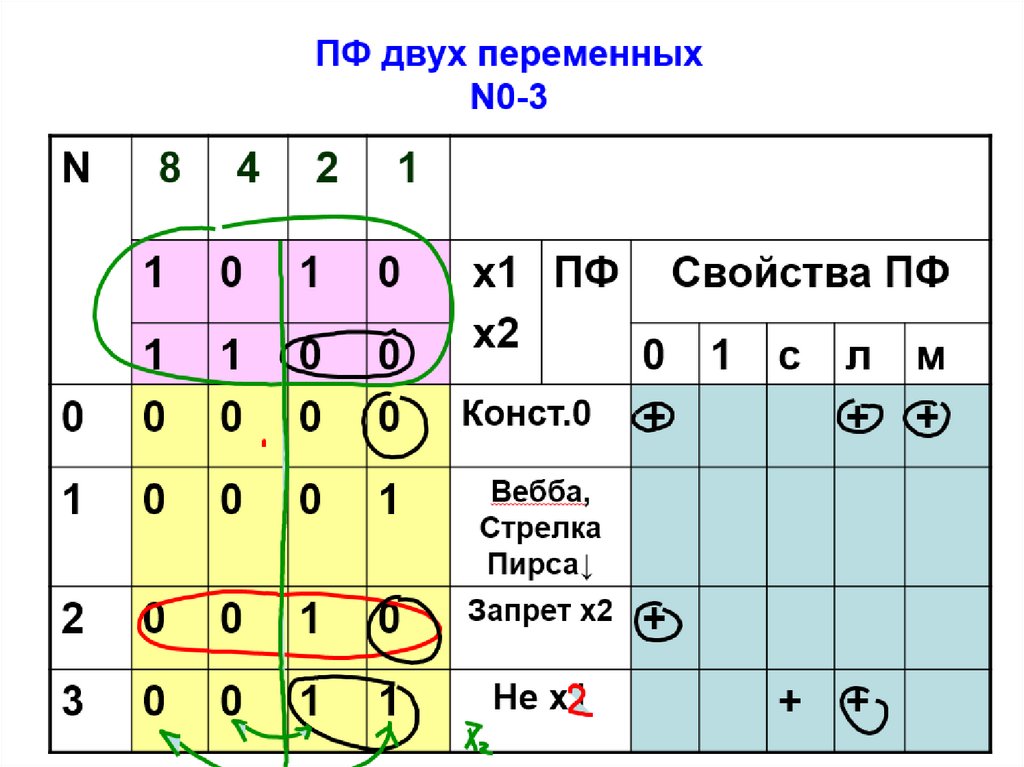
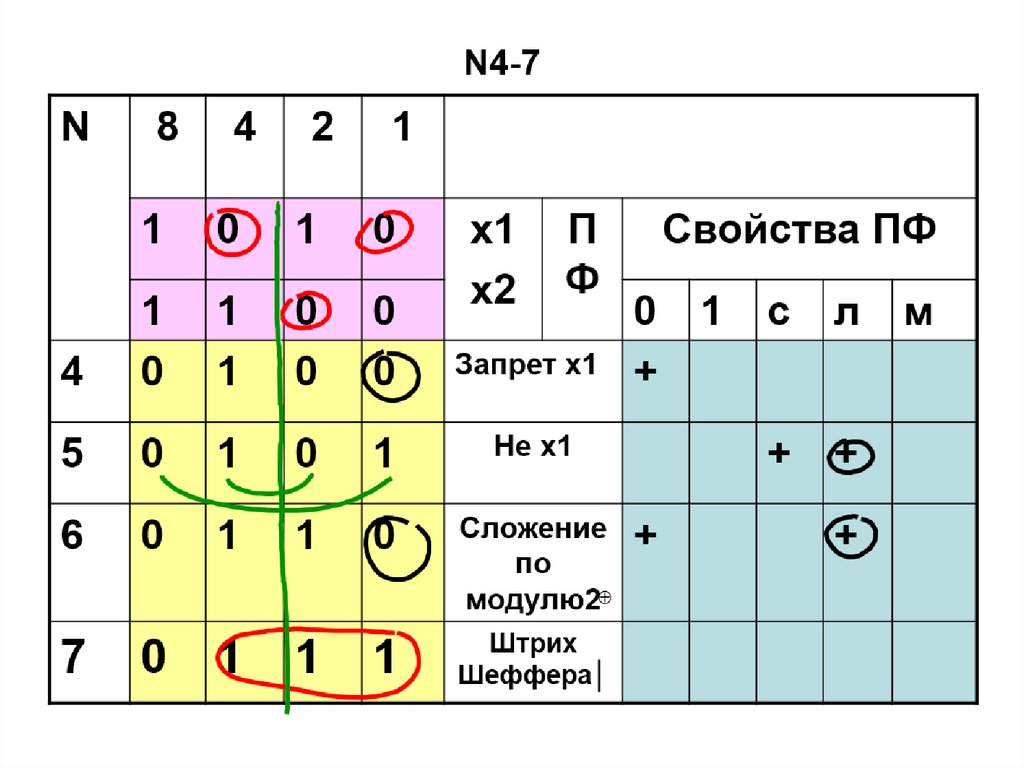
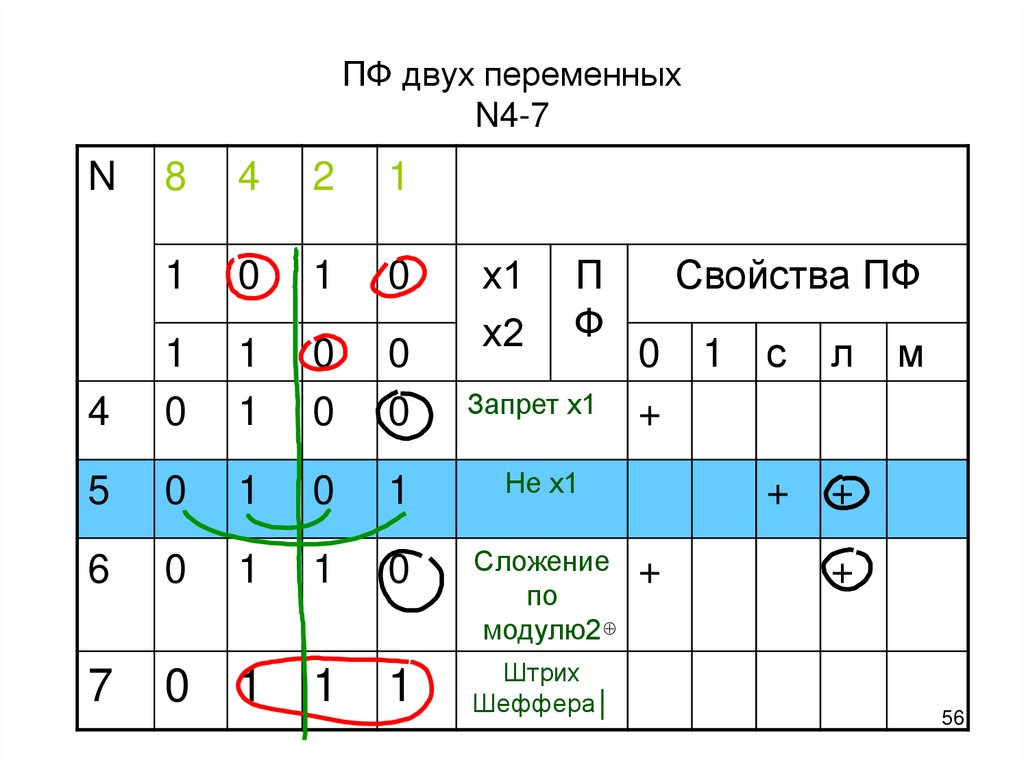
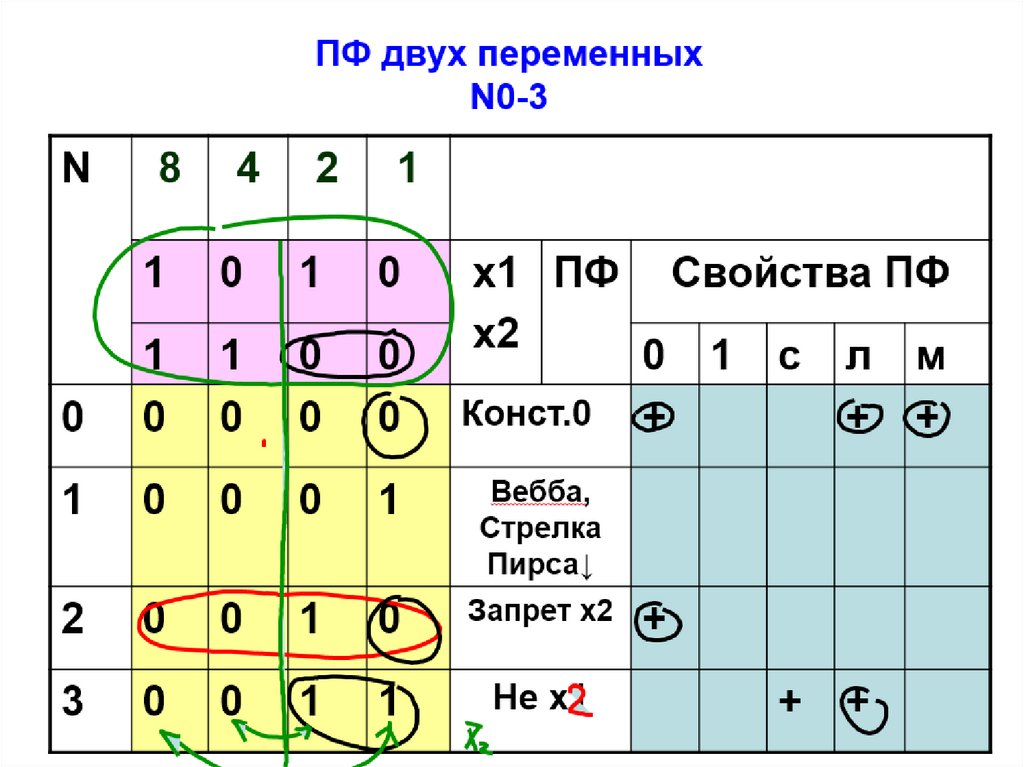
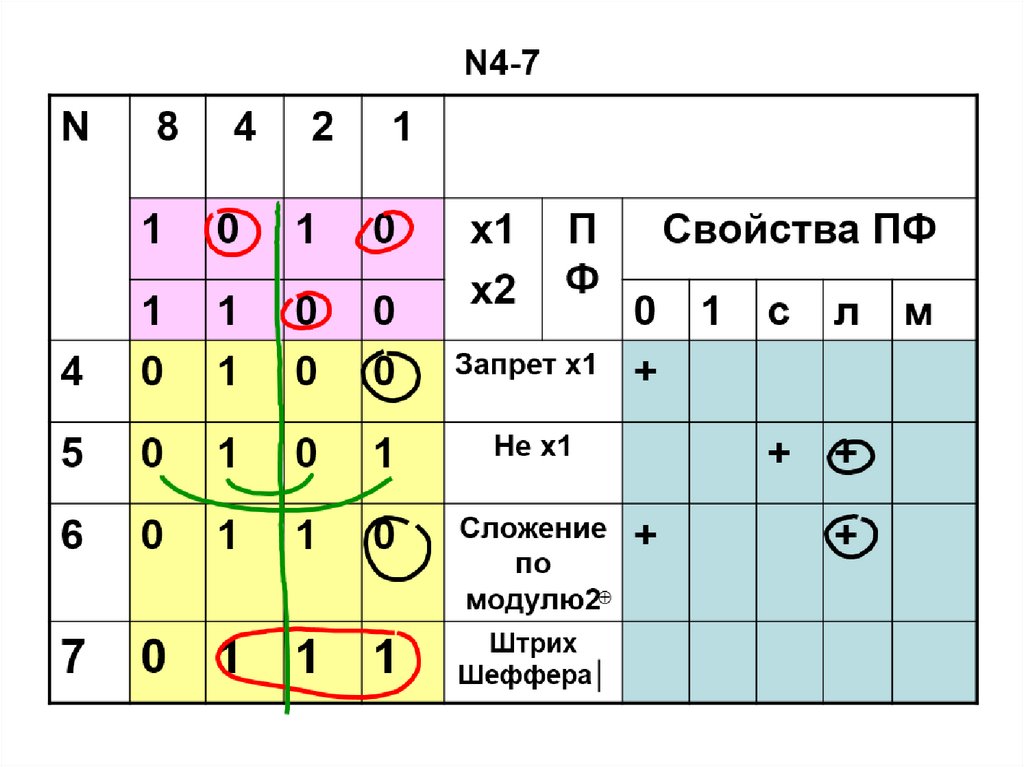
56. ПФ двух переменных N4-7
N8
4
2
1
1
0
1
0
4
1
0
1
1
0
0
0
0
Запрет х1
5
0
1
0
1
Не х1
6
0
1
1
0
Сложение
по
модулю2
1
Штрих
Шеффера│
7
0
1
1
х1
х2
П
Ф
Свойства ПФ
0
+
+
1
с
л
+
+
м
+
56
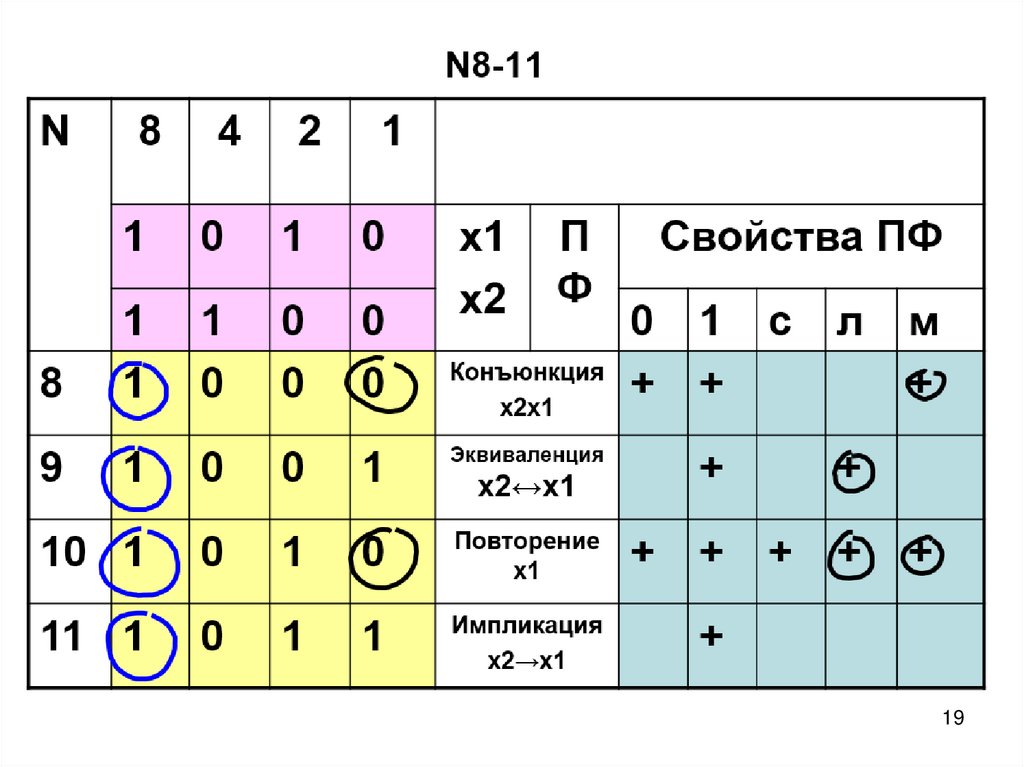
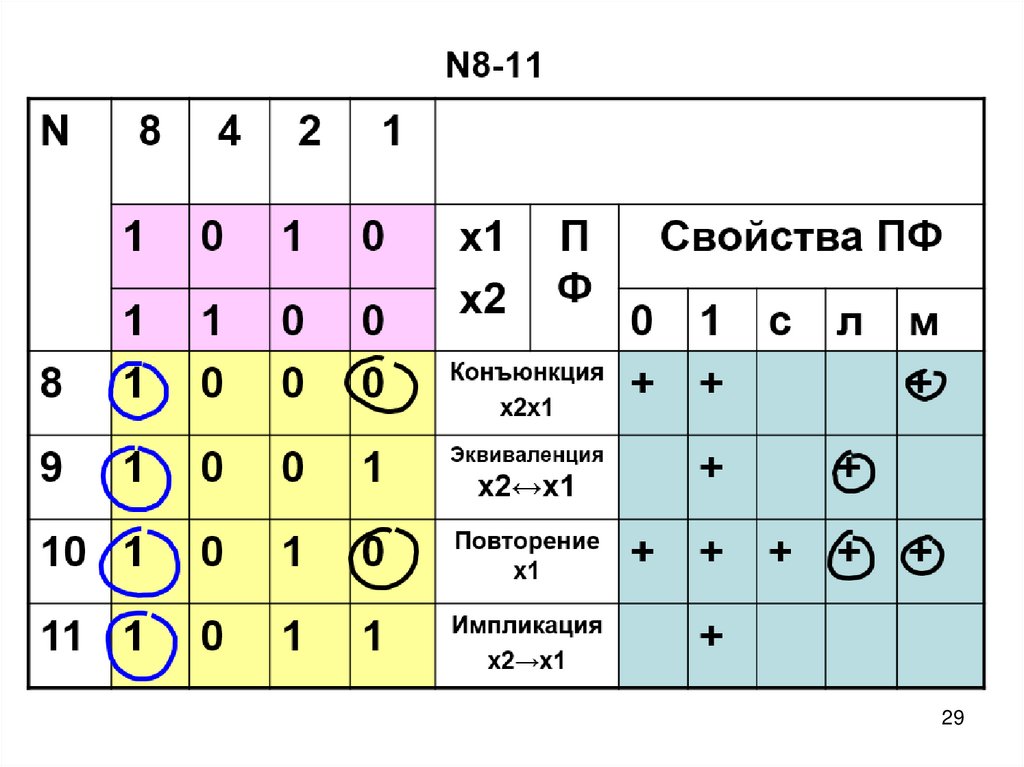
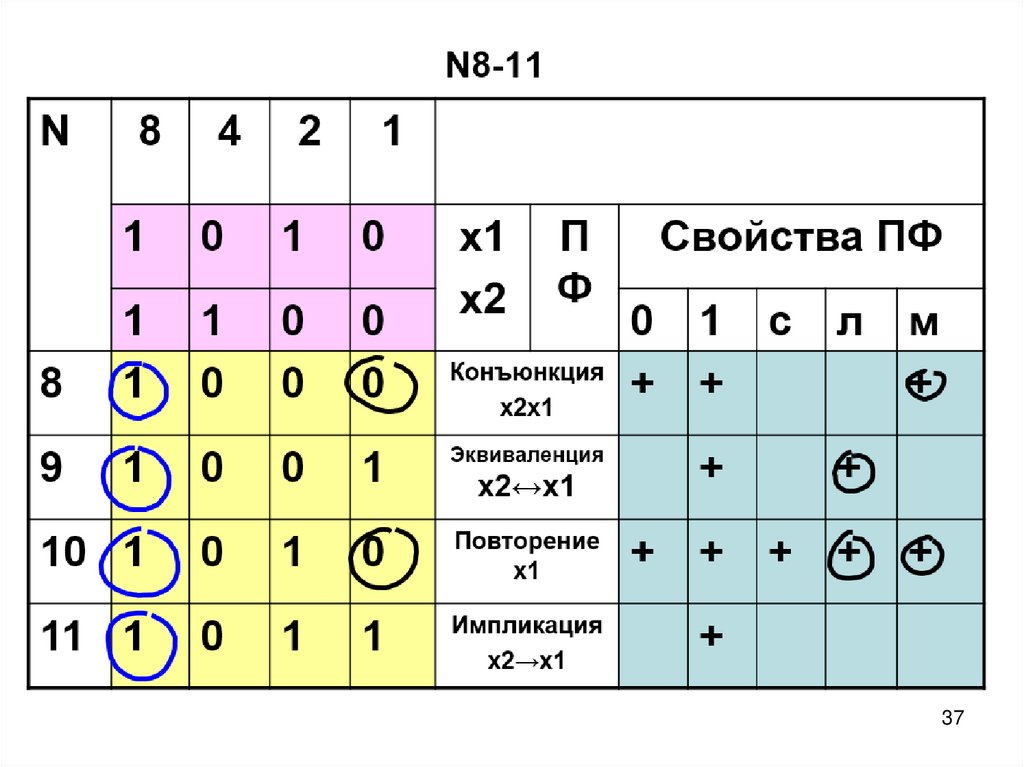
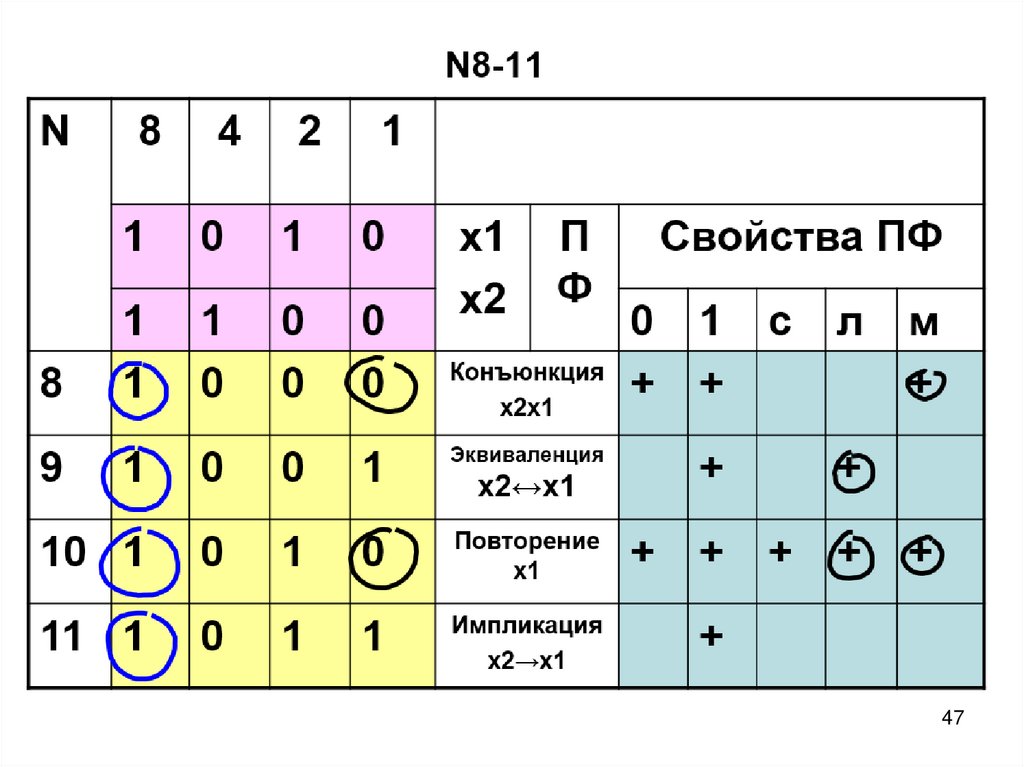
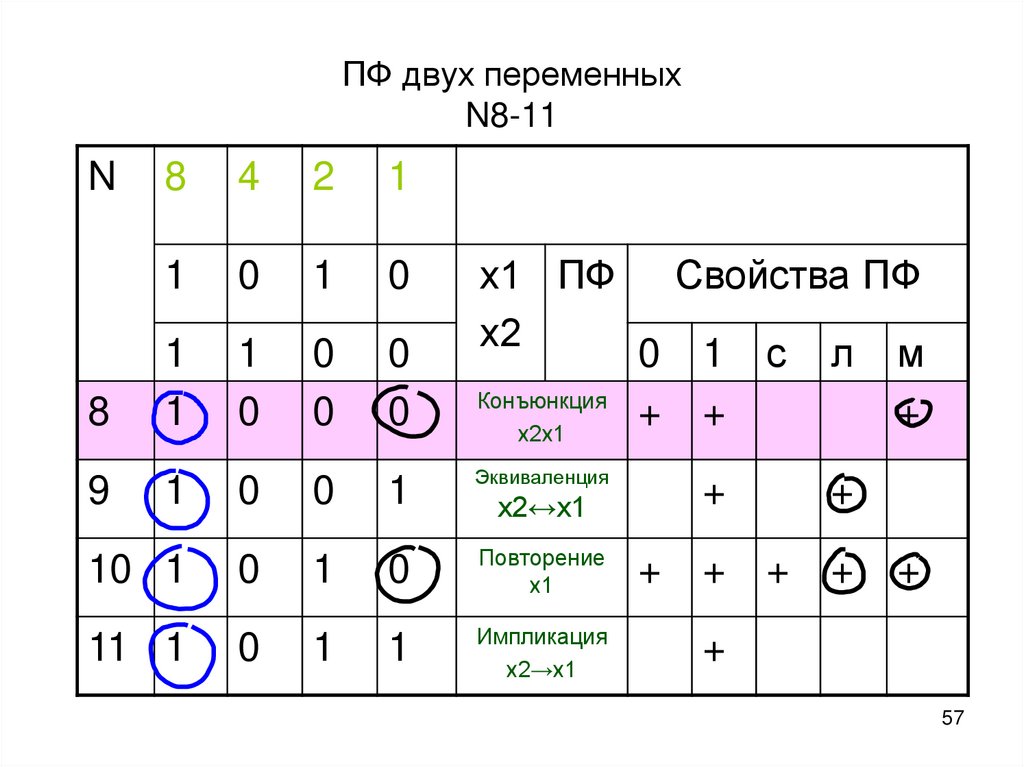
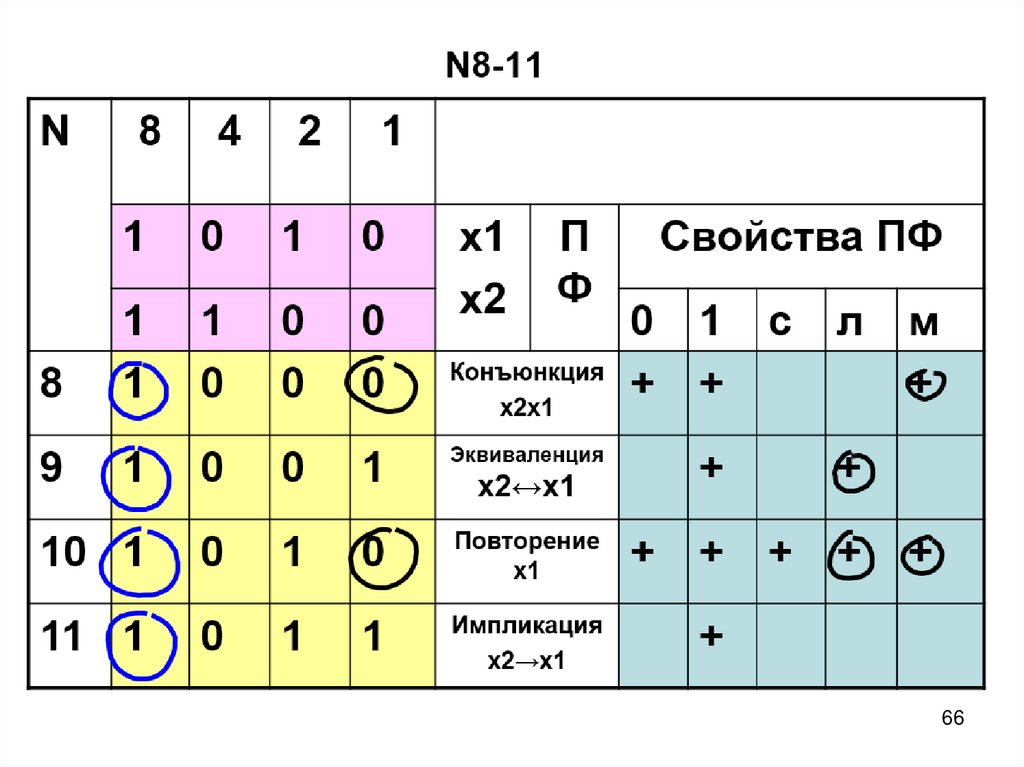
57. ПФ двух переменных N8-11
N8
4
2
1
1
0
1
0
8
1
1
1
0
0
0
0
0
9
1
0
0
1
Эквиваленция
10 1
0
1
0
Повторение
х1
11 1
0
1
1
Импликация
х2→х1
х1 ПФ
х2
Конъюнкция
х2х1
Свойства ПФ
0
+
1
+
с
+
х2↔х1
+
+
л
м
+
+
+
+
+
+
57
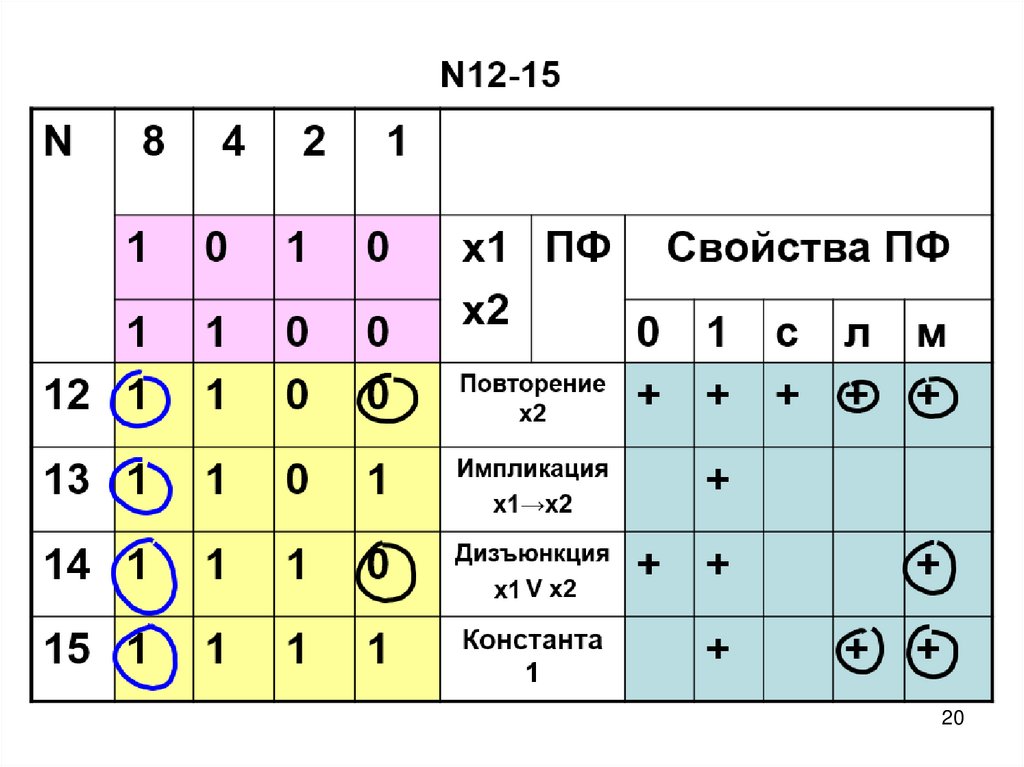
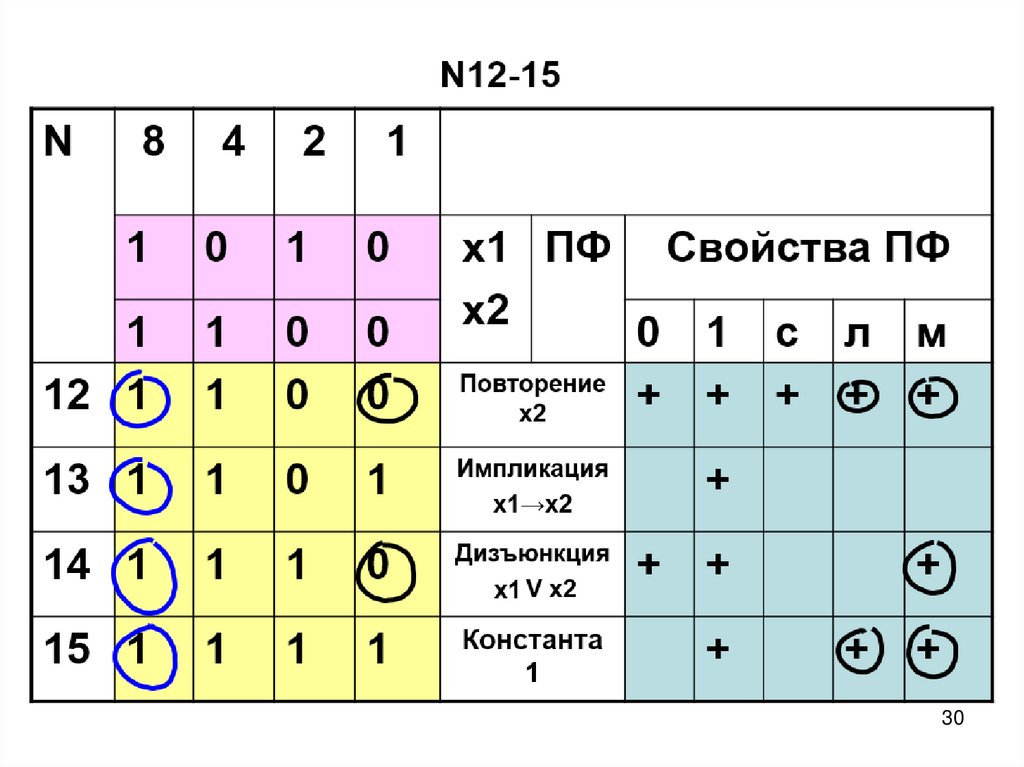
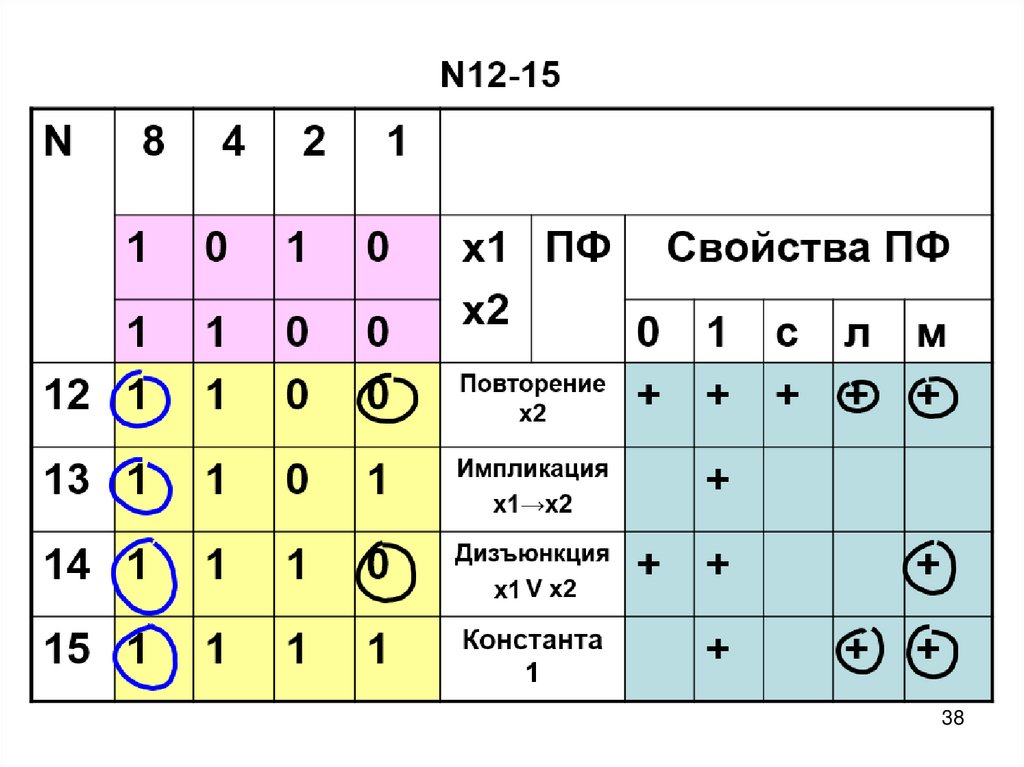
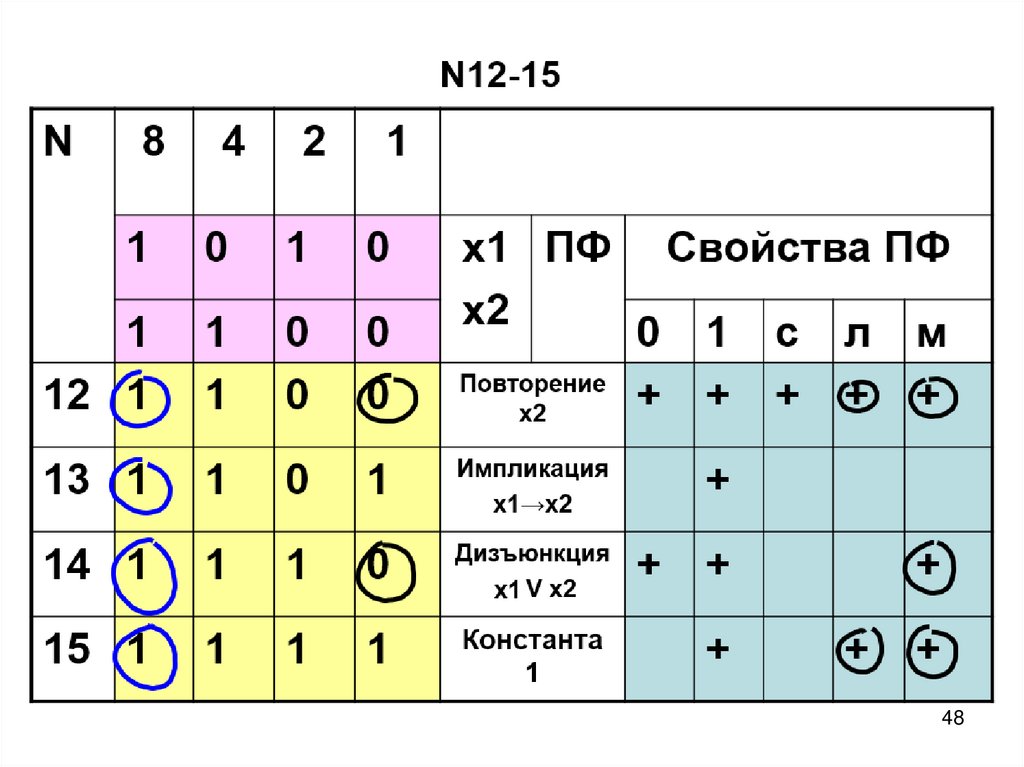
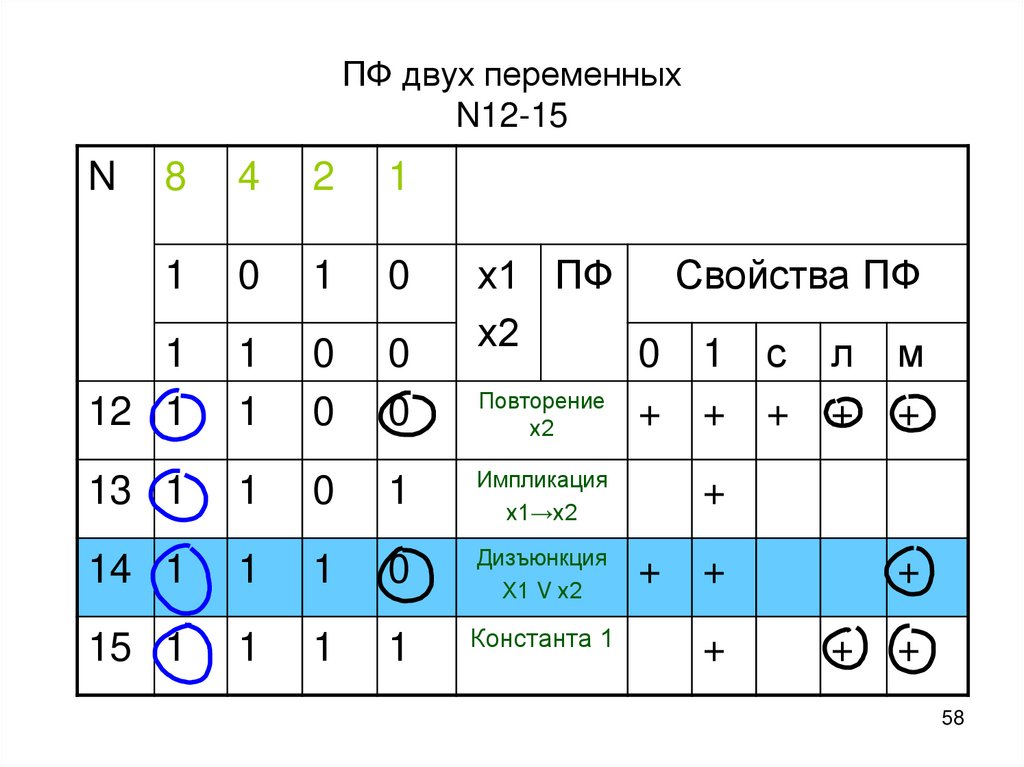
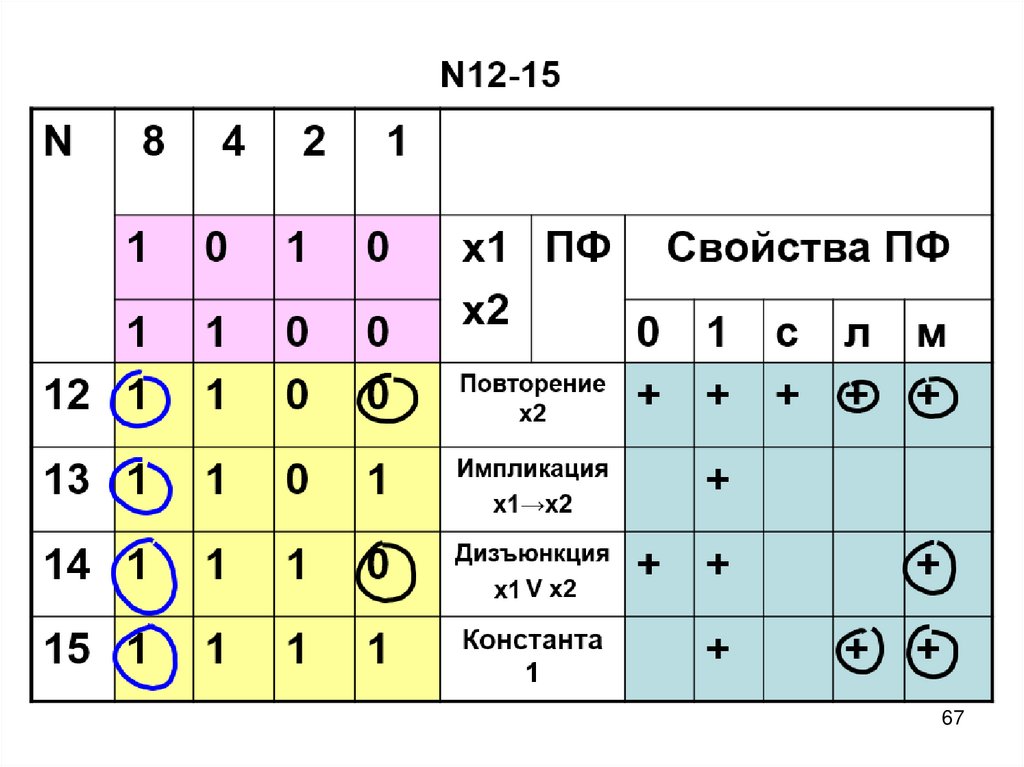
58. ПФ двух переменных N12-15
N8
4
2
1
1
0
1
0
1
12 1
1
1
0
0
0
0
13 1
1
0
1
Импликация
х1→х2
14 1
1
1
0
Дизъюнкция
Х1 V х2
15 1
1
1
1
Константа 1
х1 ПФ
х2
Повторение
х2
Свойства ПФ
0
+
1
+
с
+
л
+
м
+
+
+
+
+
+
+
+
58
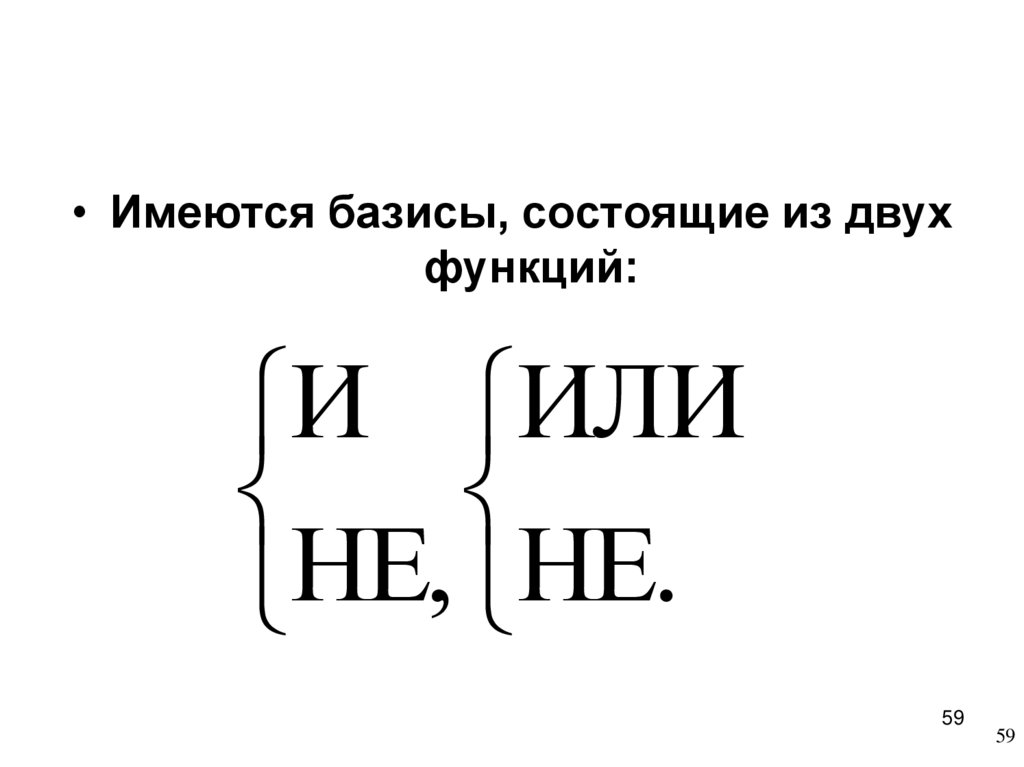
59.
• Имеются базисы, состоящие из двухфункций:
И ИЛИ
НЕ,
НЕ.
59
59
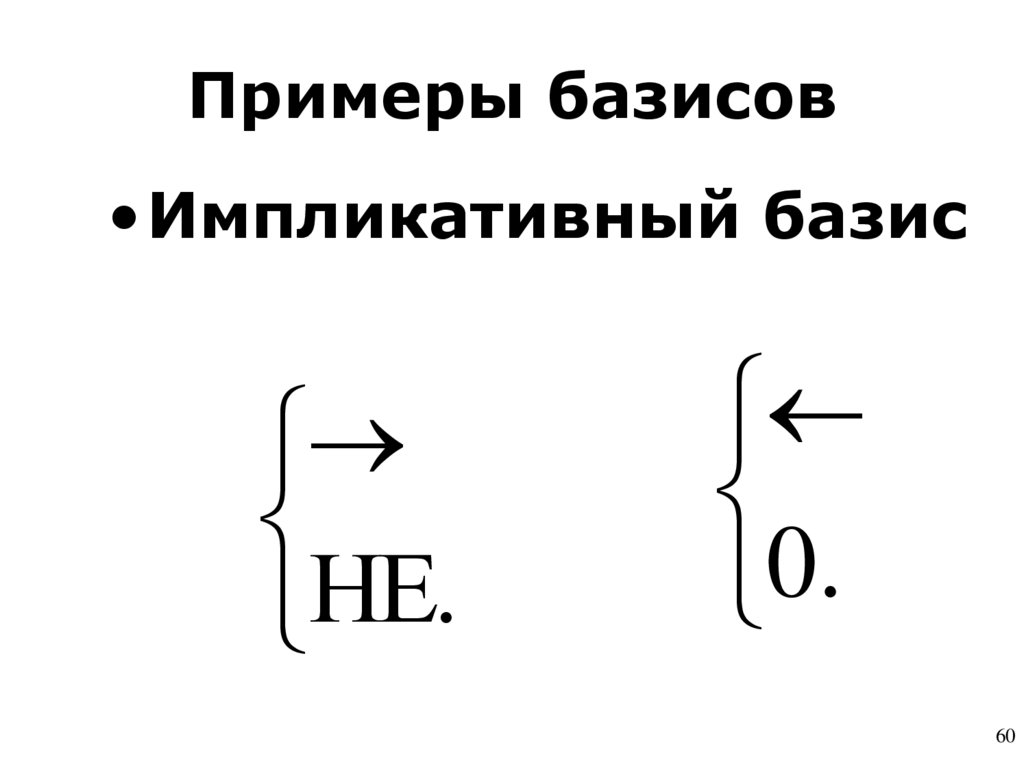
60. Примеры базисов
•Импликативный базисНЕ.
0.
60
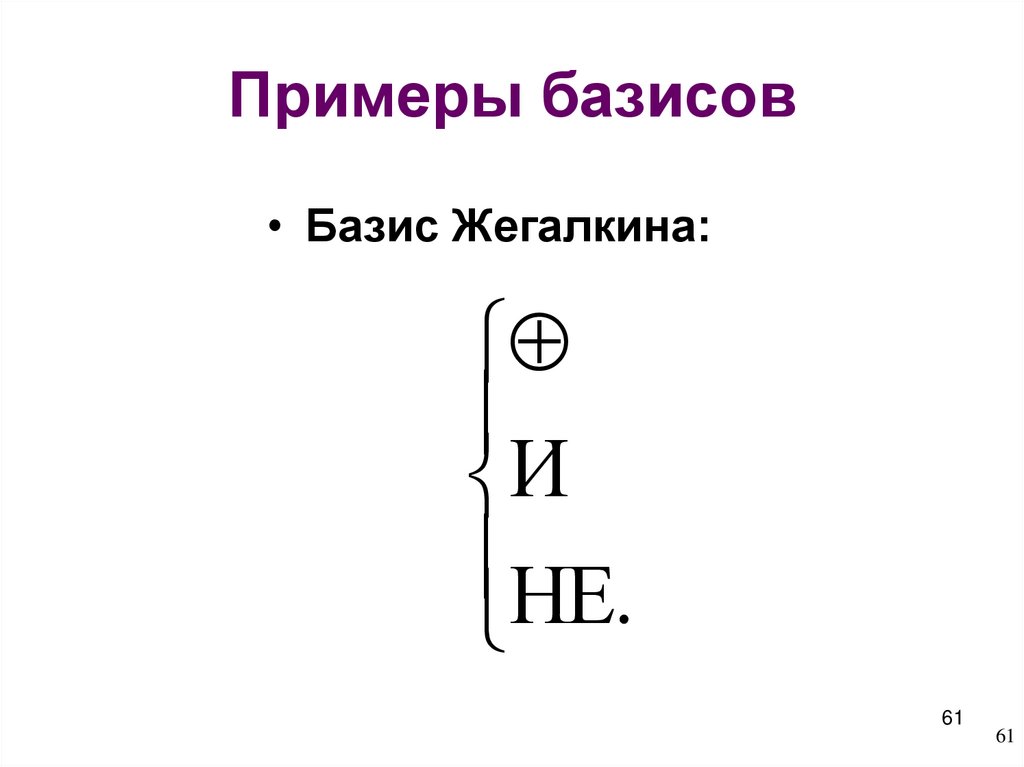
61. Примеры базисов
• Базис Жегалкина:И
НЕ.
61
61
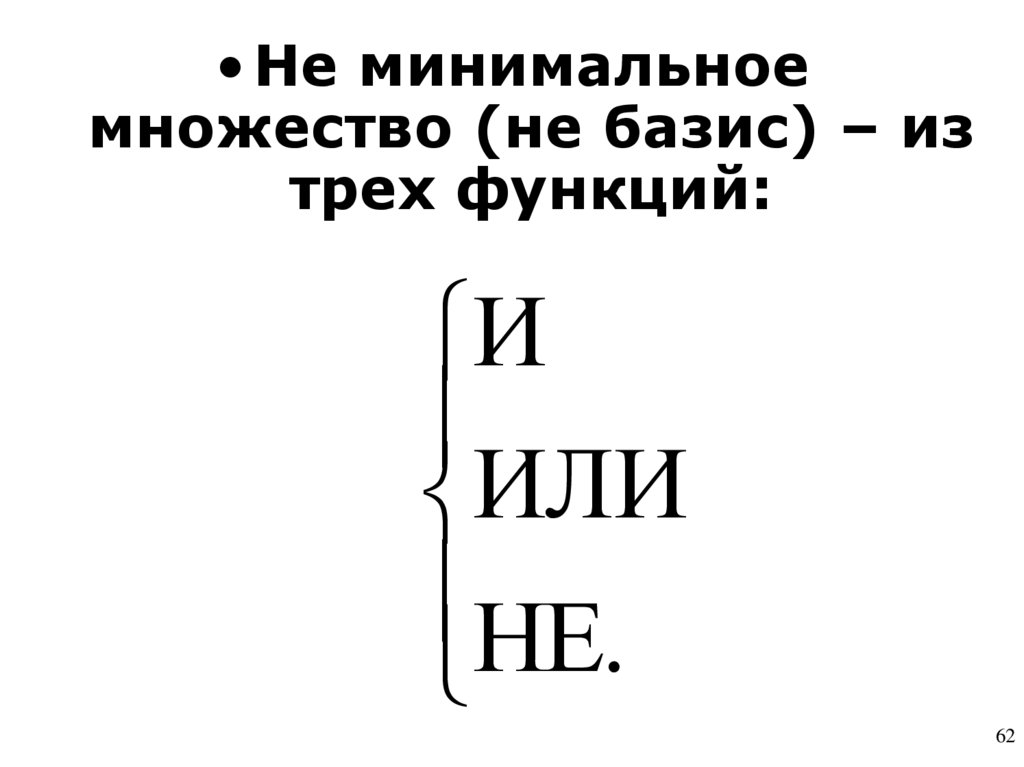
62.
• Не минимальноемножество (не базис) – из
трех функций:
И
ИЛИ
НЕ.
62
63.
• Имеются функции,обладающие всеми пятью
отмеченными свойствами.
Таковы функции .
• Часто их называют
соответственно ИЛИ-НЕ, ИНЕ.
• Таким образом, это базисы,
состоящие из одной
функции.
63
64.
6465.
6566.
6667.
6768.
•Т3.МИНИМИЗАЦИЯ
ФОРМУЛ ЛОГИКИ
ВЫСКАЗЫВАНИЙ
69. С.118-145
70. С.62-102
71.
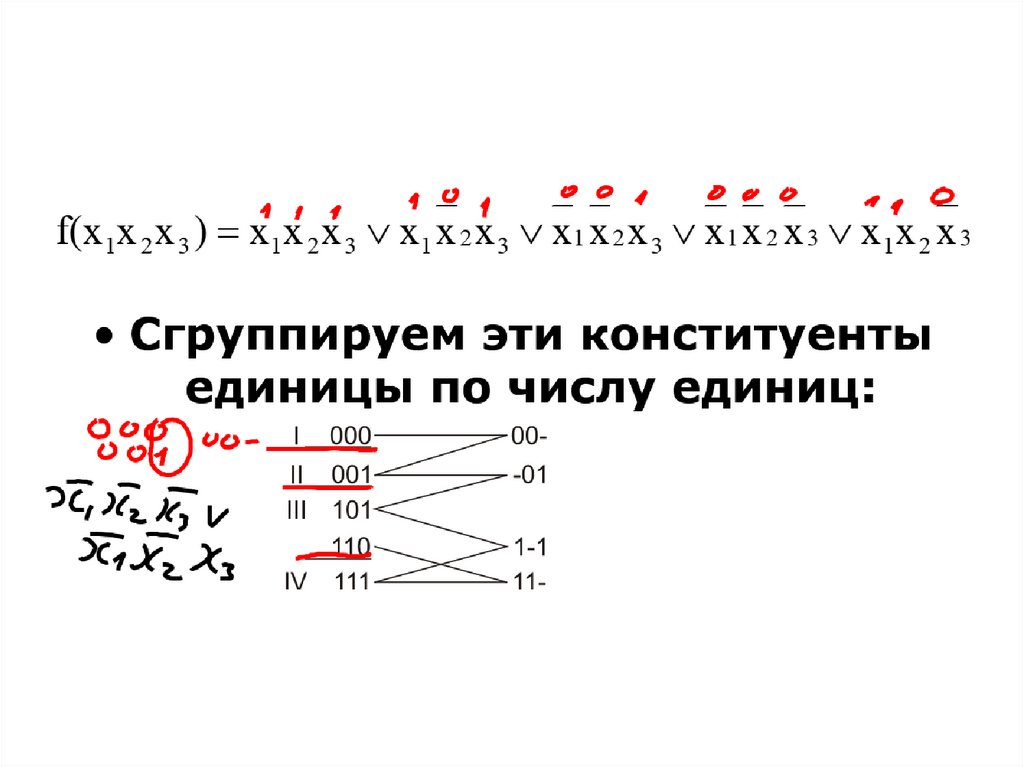
•Метод КвайнаМак-Класки.71
72. Willard Van Orman Quine (1908-2000), McCluskey (1929-2016)
73.
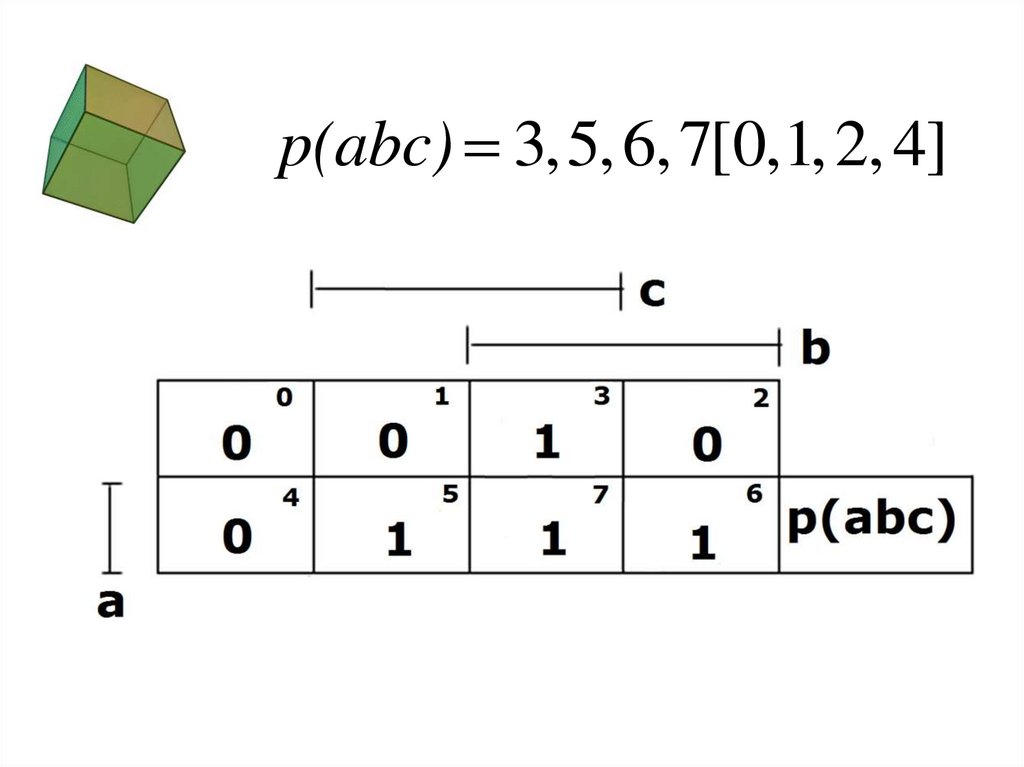
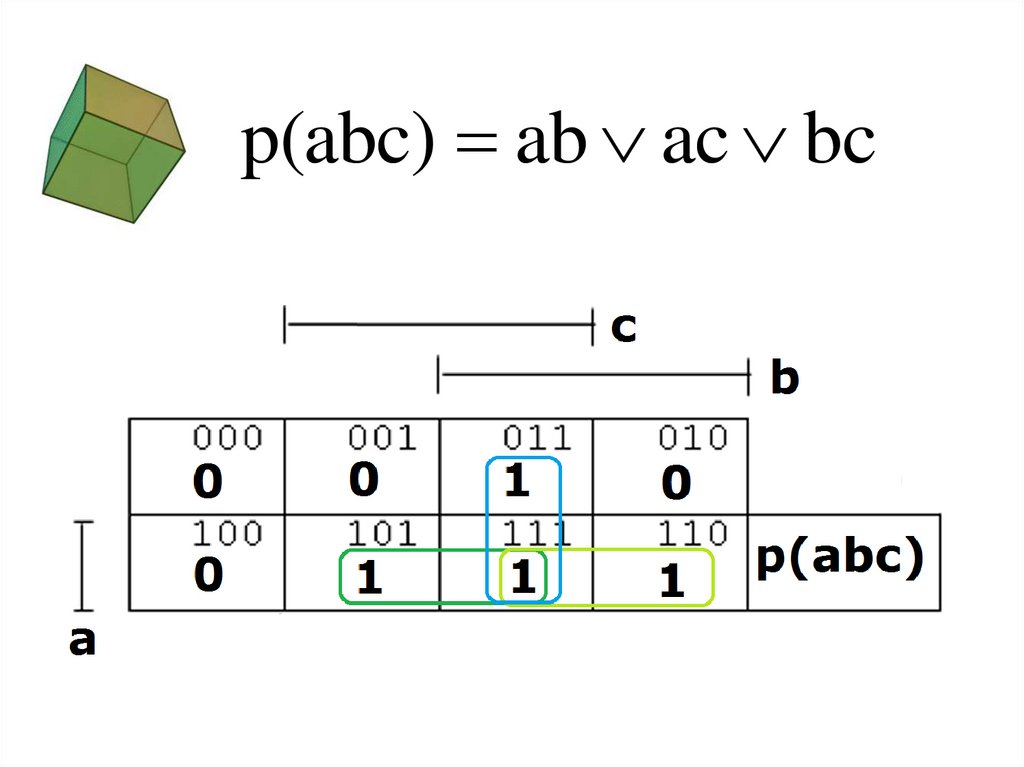
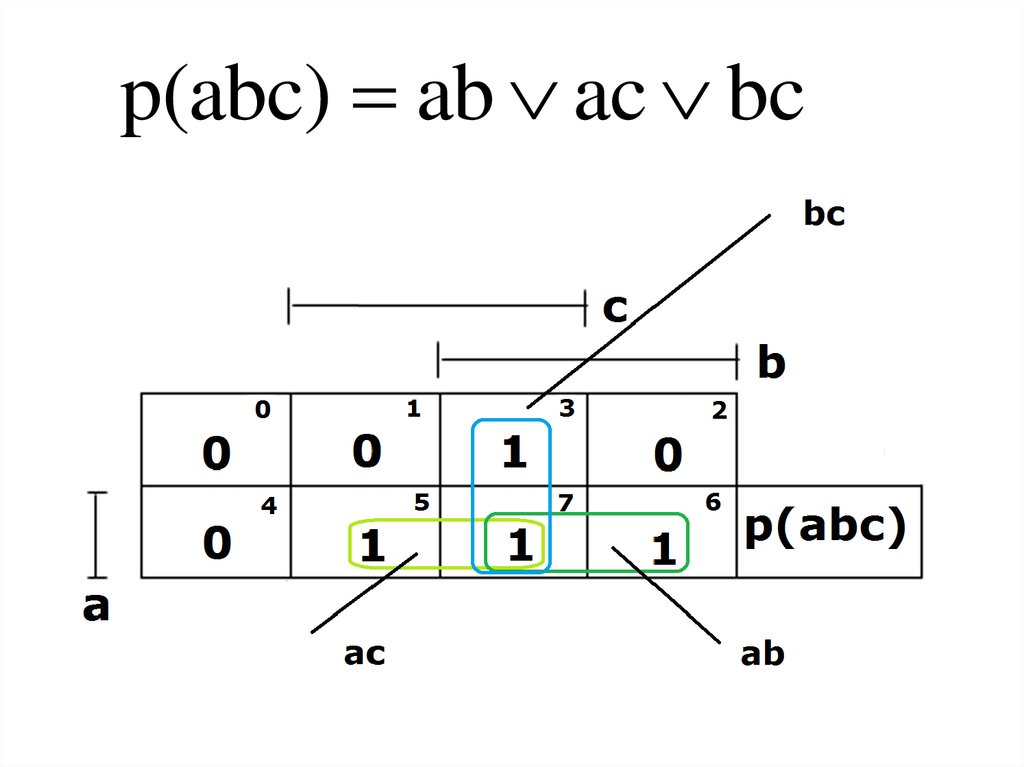
p(abc)2 011,101,110,11174.
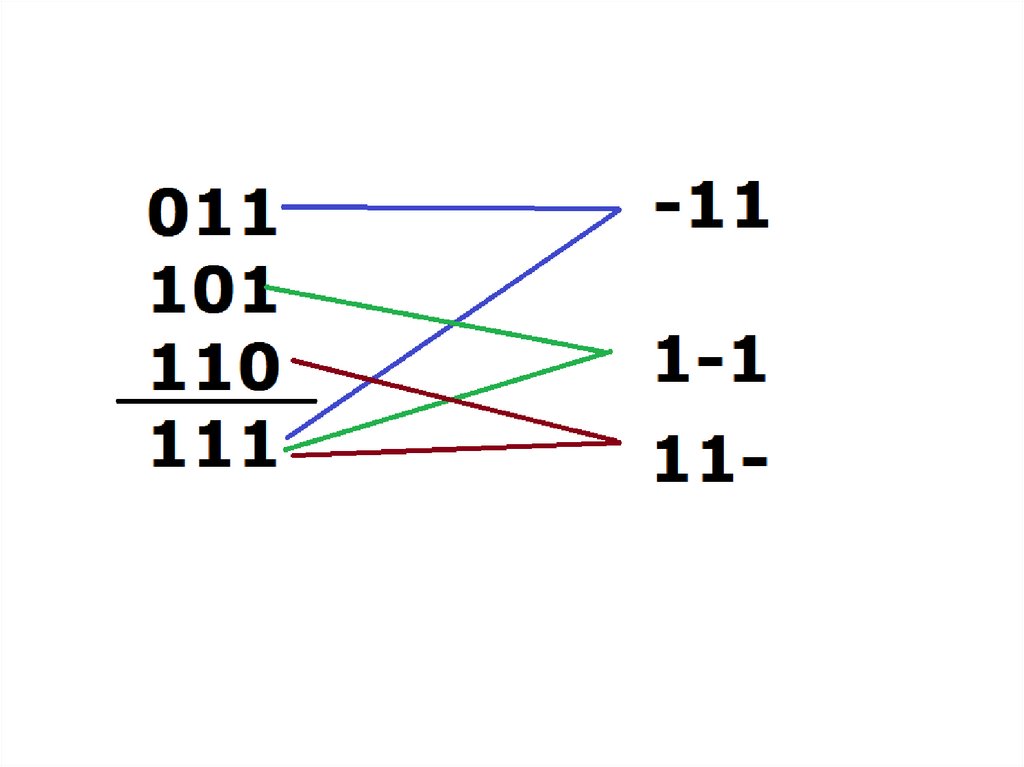
75. Таблица Квайна
p(abc) ( 11) (1 1) (11 )p(abc) bc ab ac
76.
77.
78.
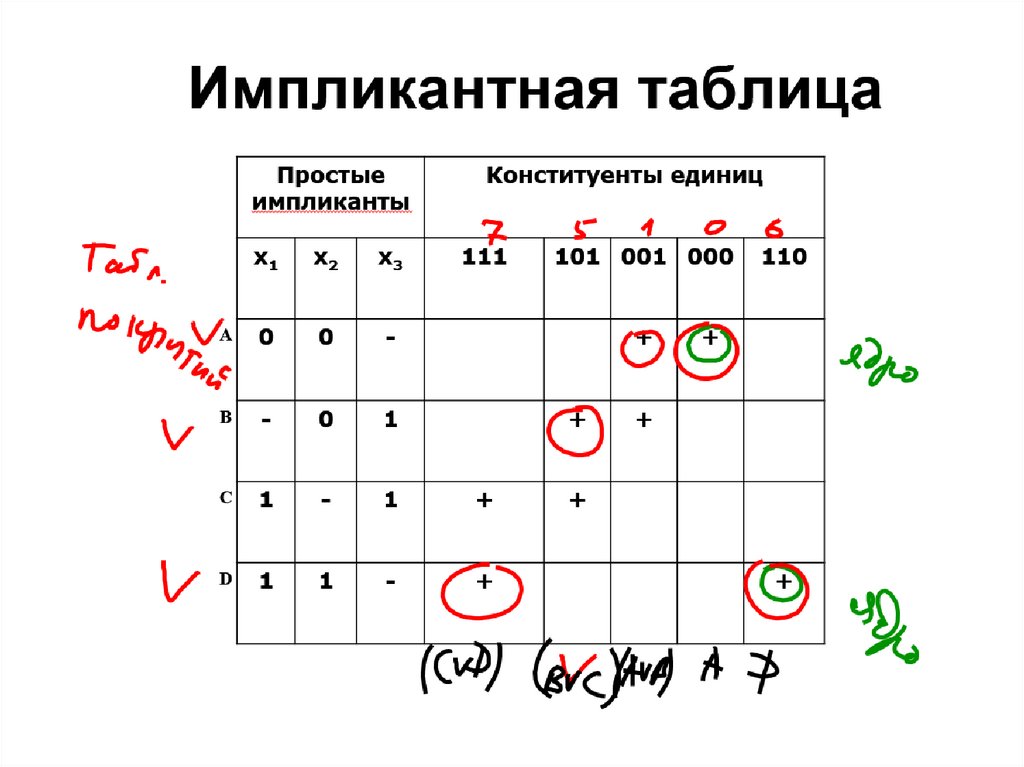
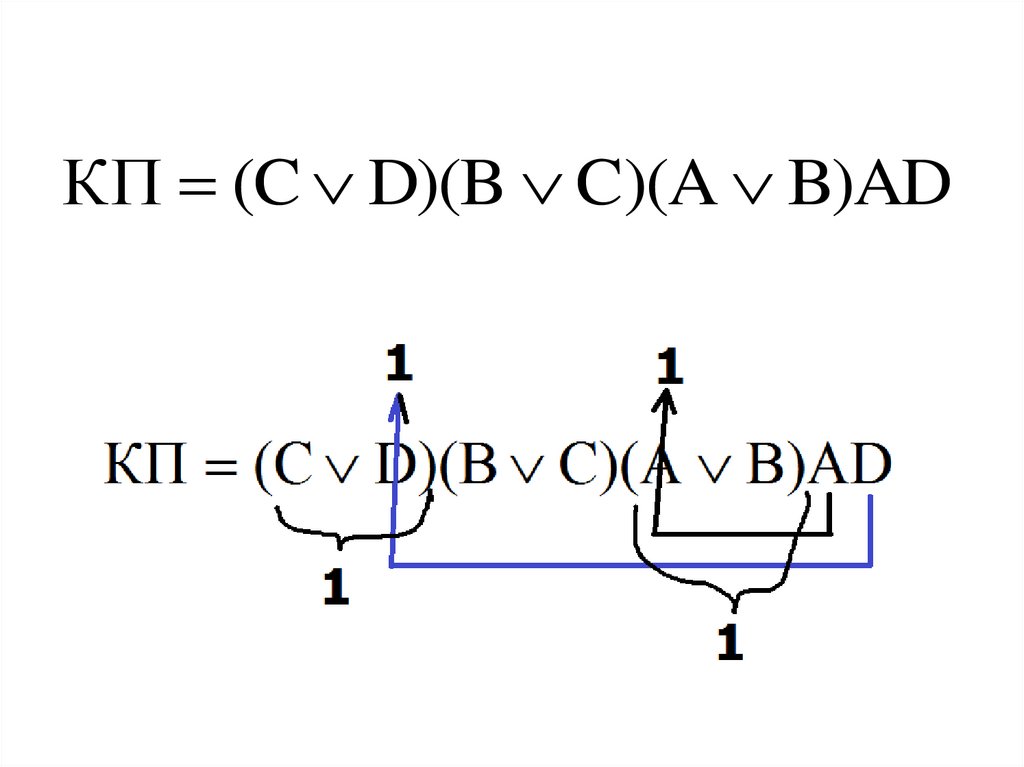
КП (C D)(B C)(A B)AD ?79.
КП (C D)(B C)(A B)AD80.
КП (B C)ADf1 x 2 x 3 x1 x 2 x1x 2
f 2 x1x 3 x1 x 2 x1x 2
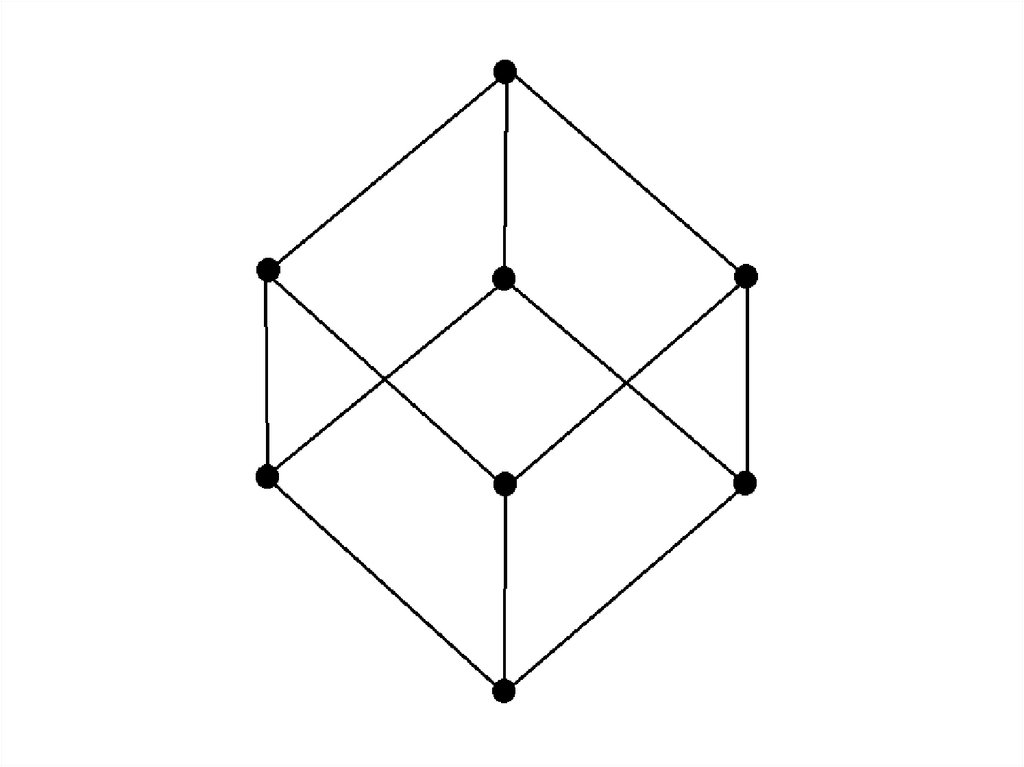
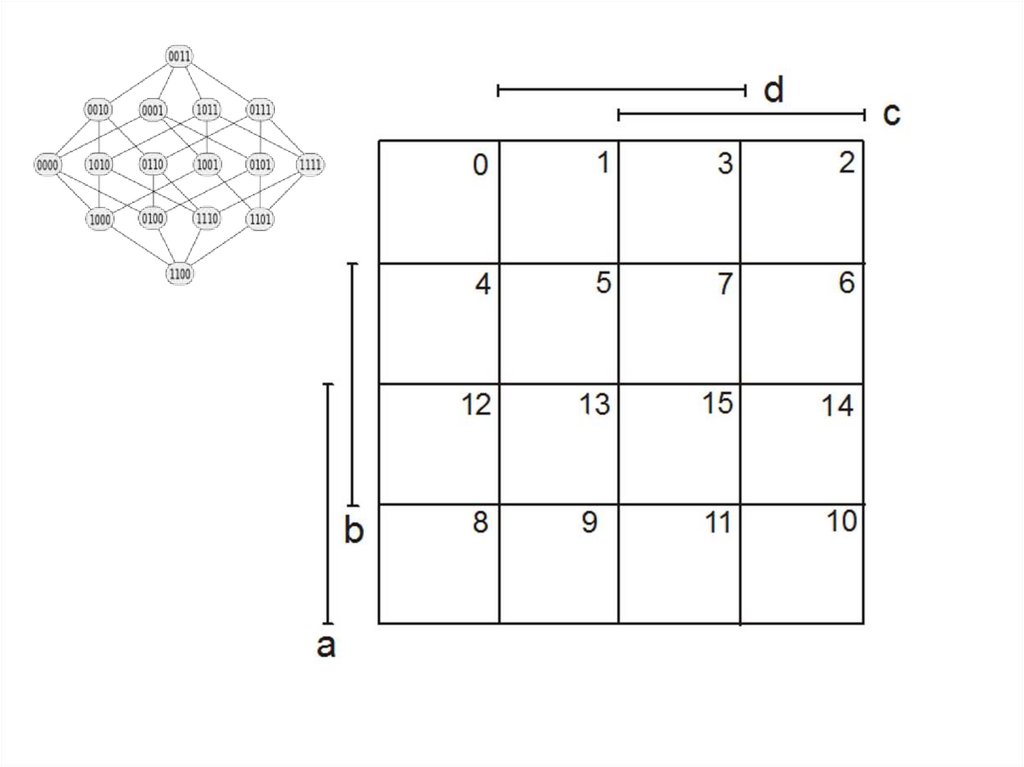
81.
•Минимизацияпо кубу
соседних
чисел
82.
83.
84.
85.
86.
87.
88.
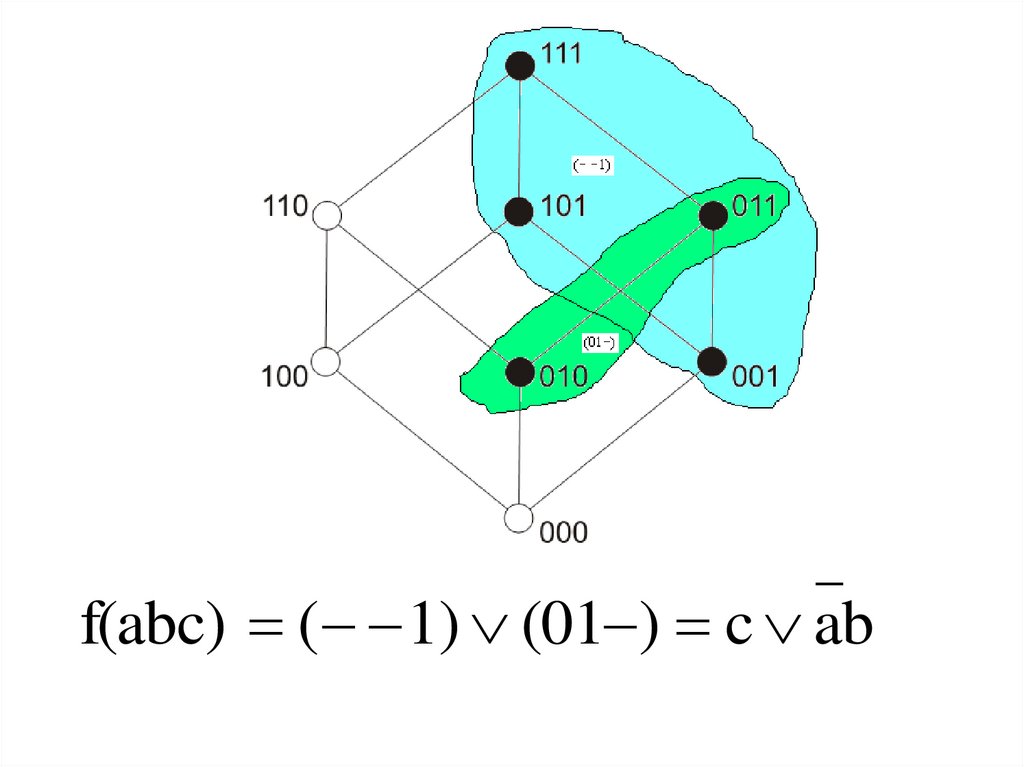
f(abc) ( 1) (01 ) c ab89.
МИНИМИЗАЦИЯПО
КАРТАМ КАРНО
90.
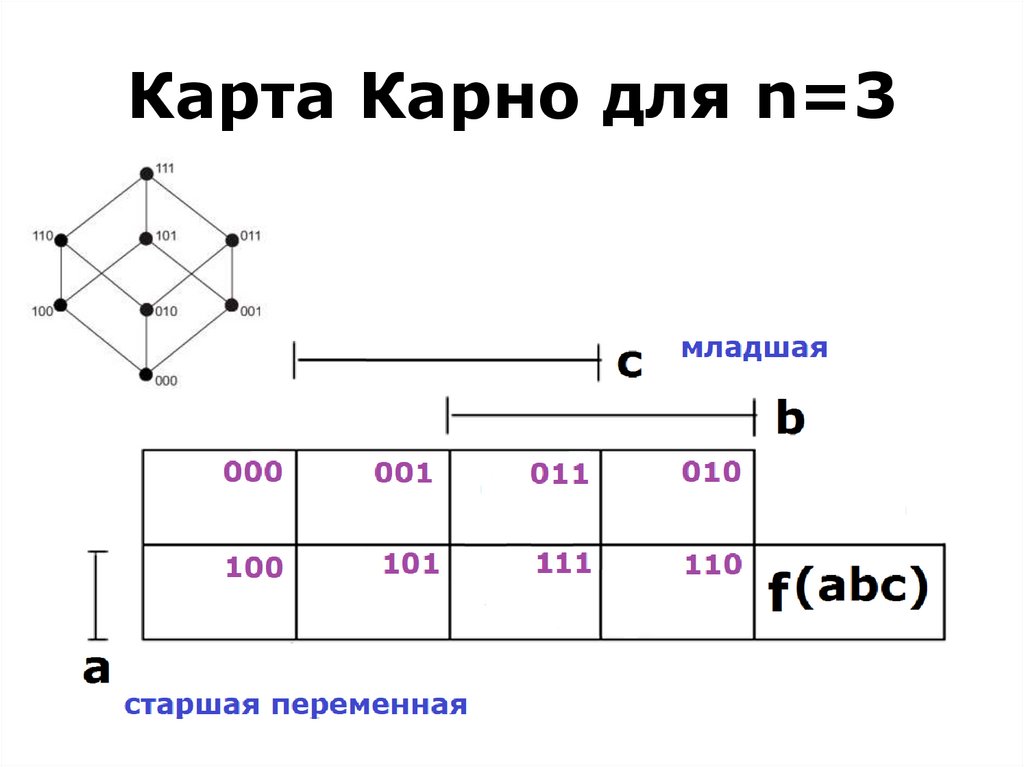
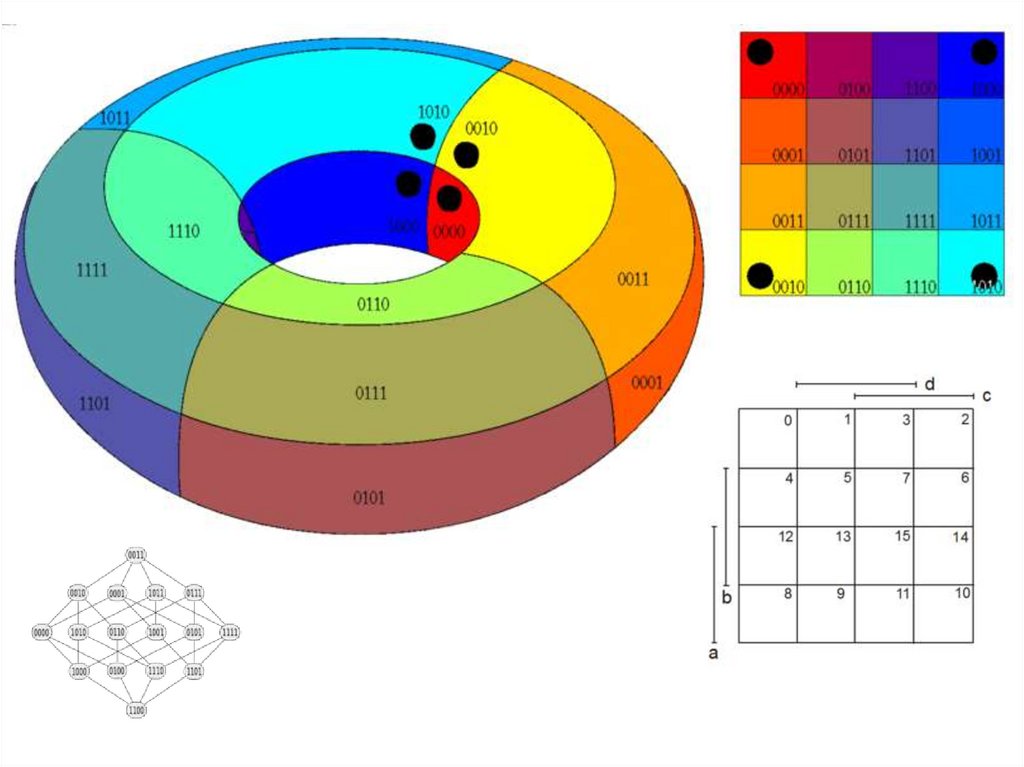
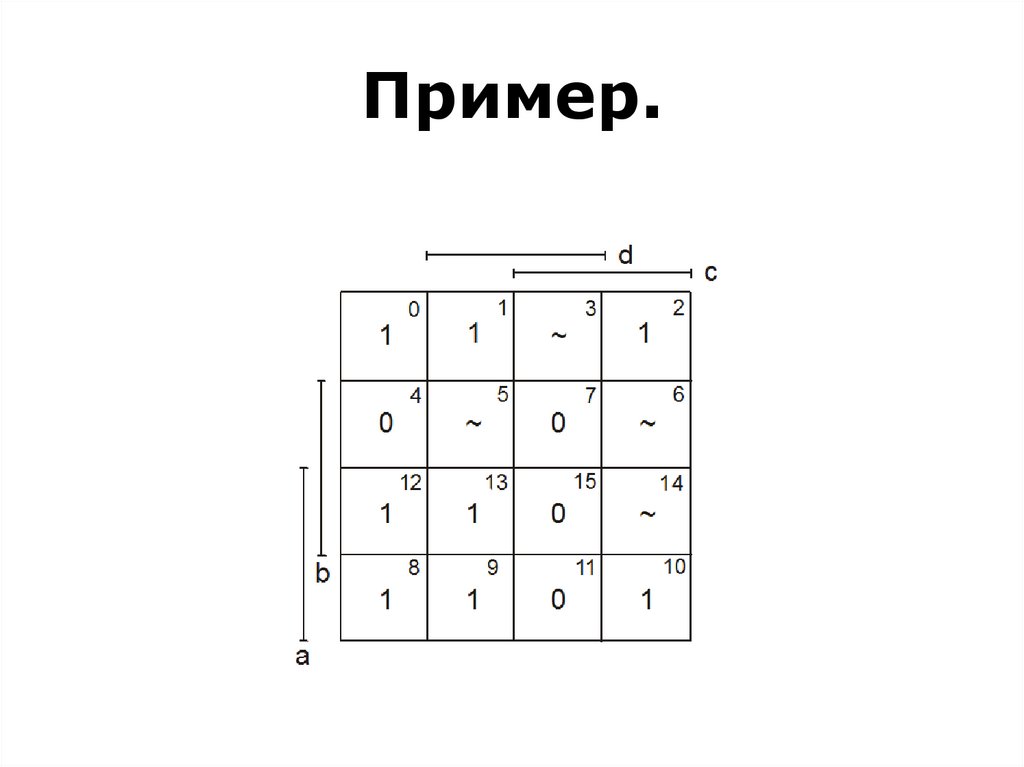
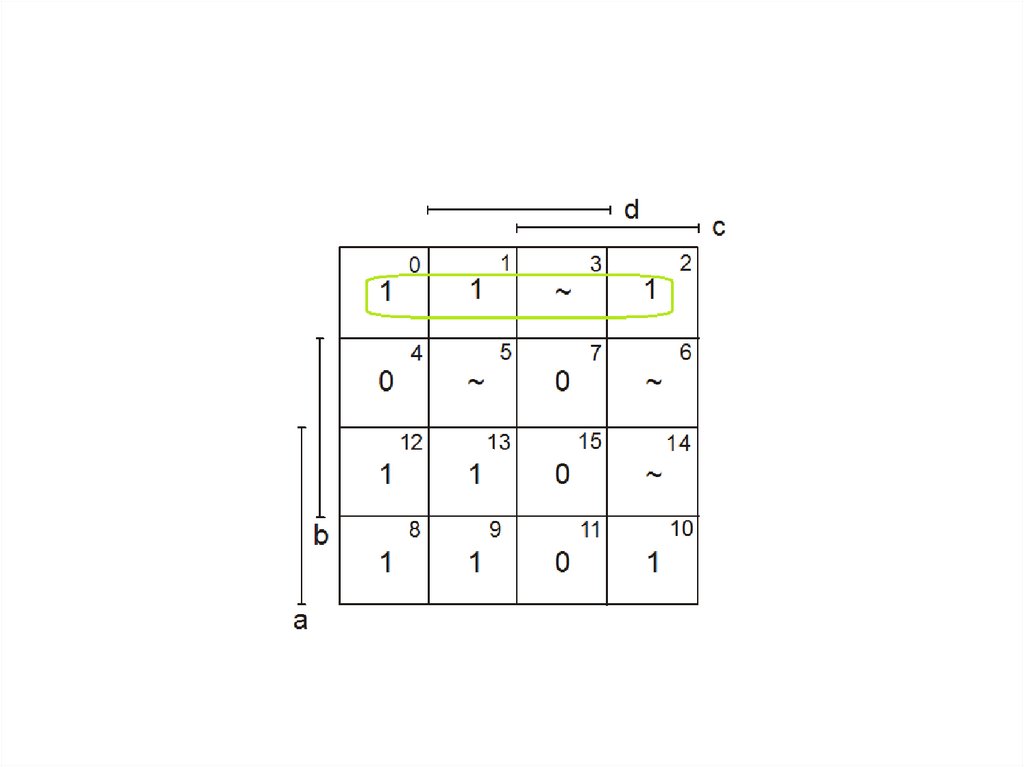
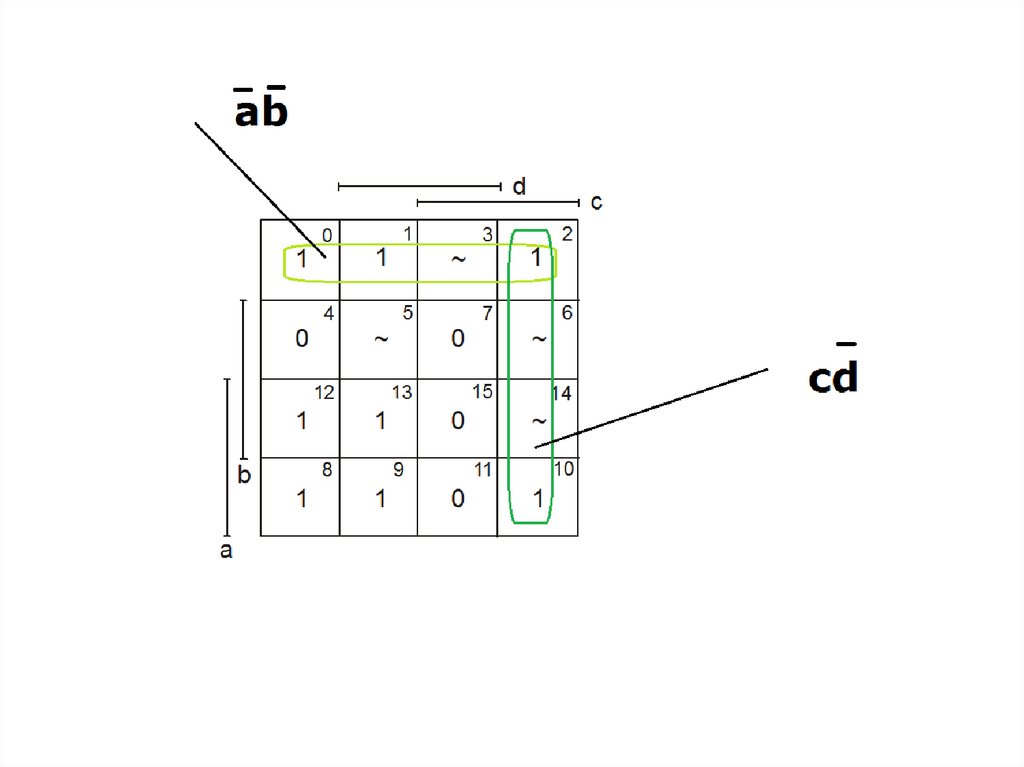
91. Maurice Karnaugh (1924) is an American physicist, famous for the Karnaugh map used in Boolean algebra.
92. Edward W. Veitch (1924 –2013) was an American computer scientist.
Edward W. Veitch (1924 –2013)was an American computer
scientist.














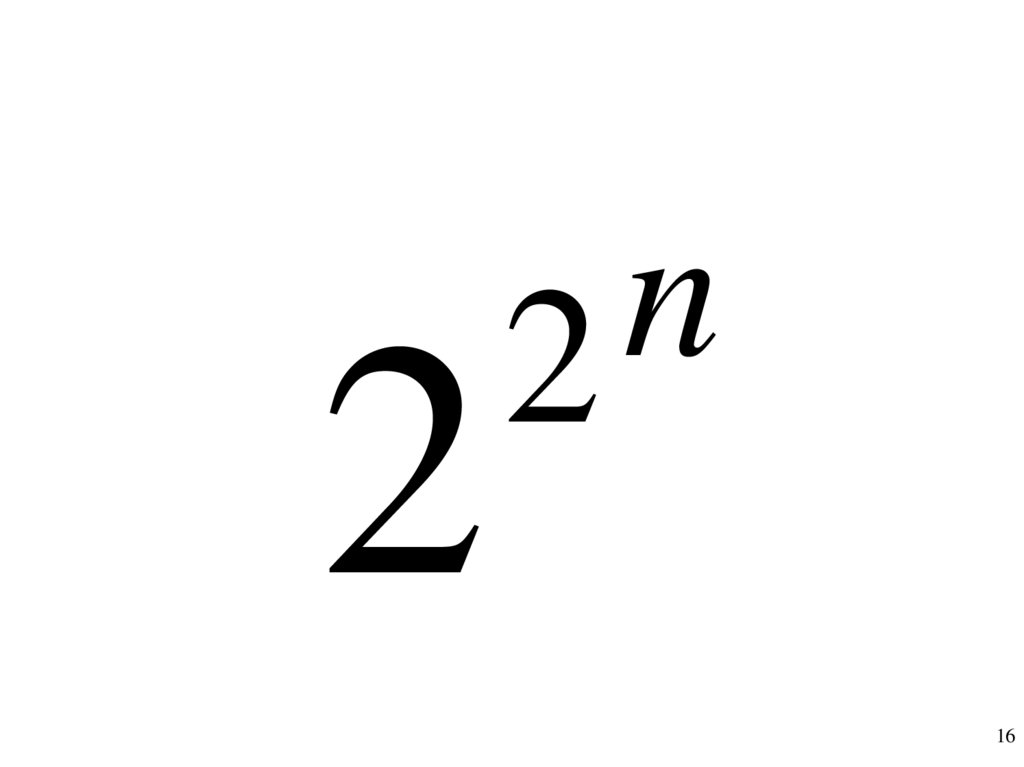







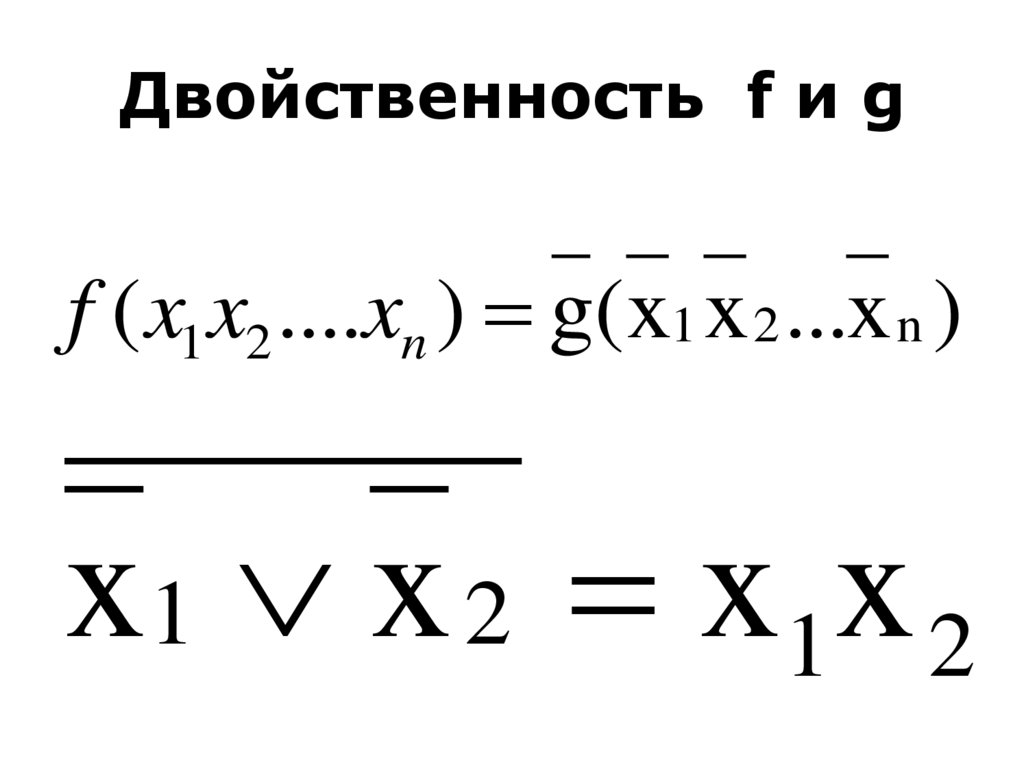
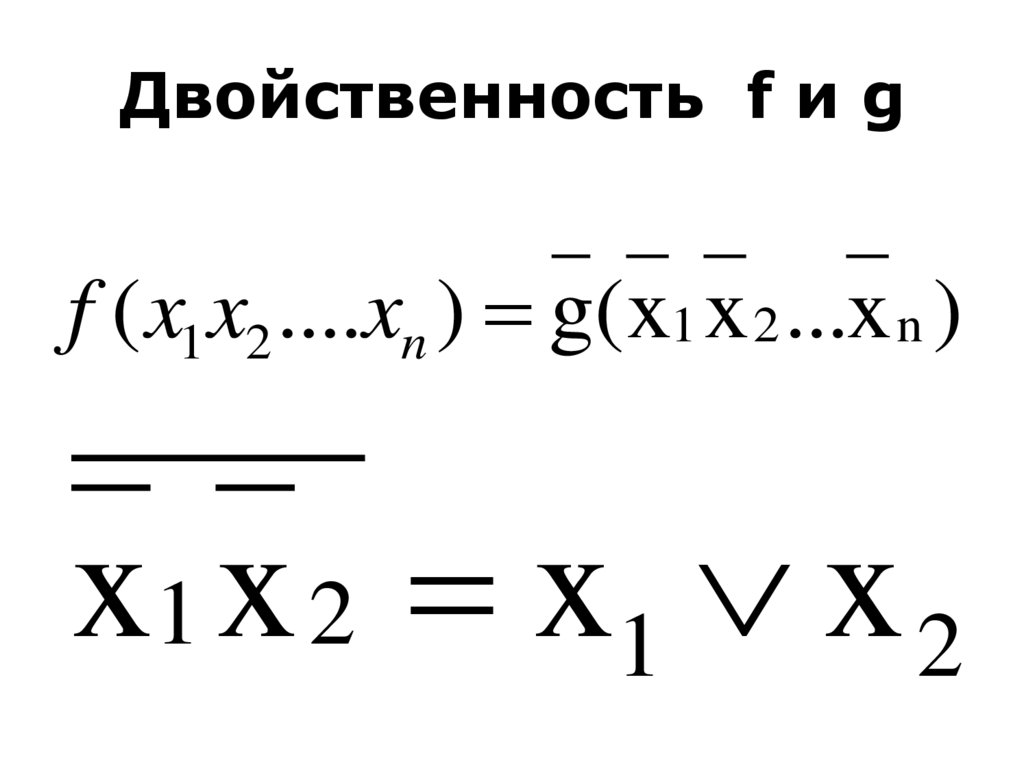
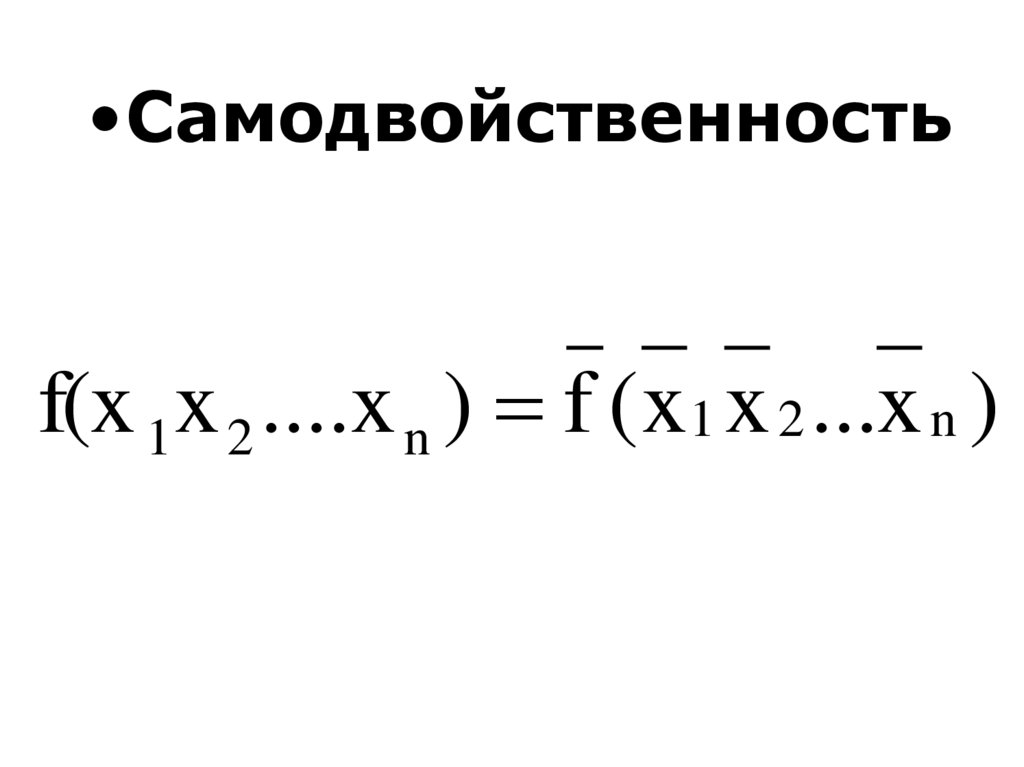















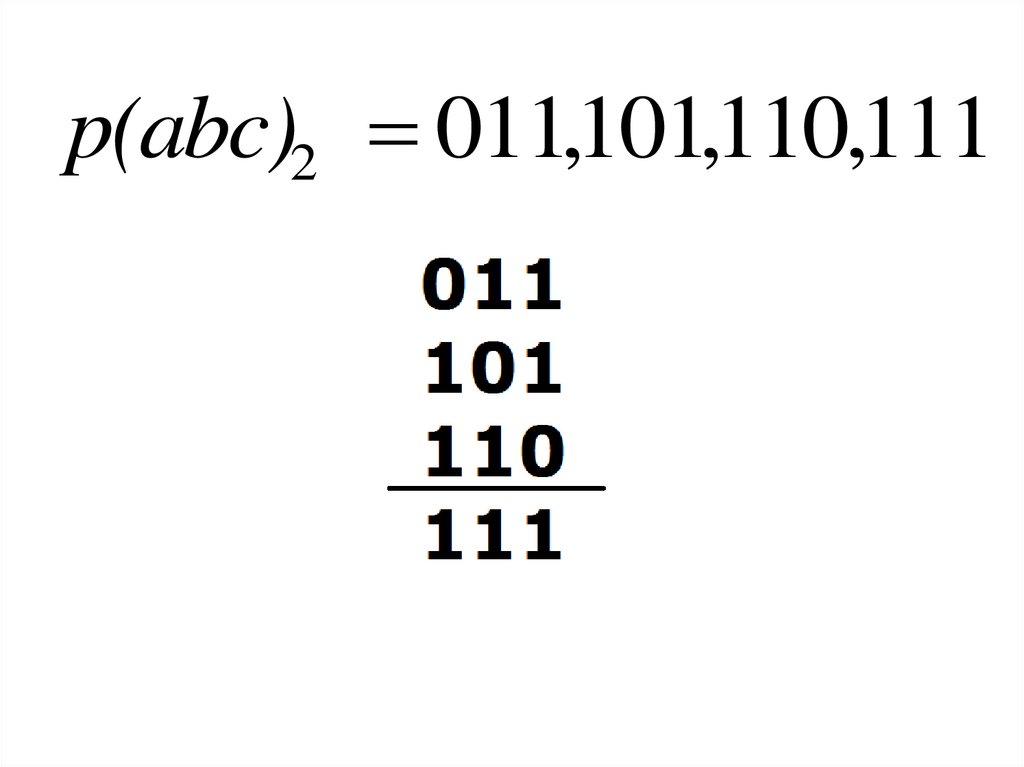

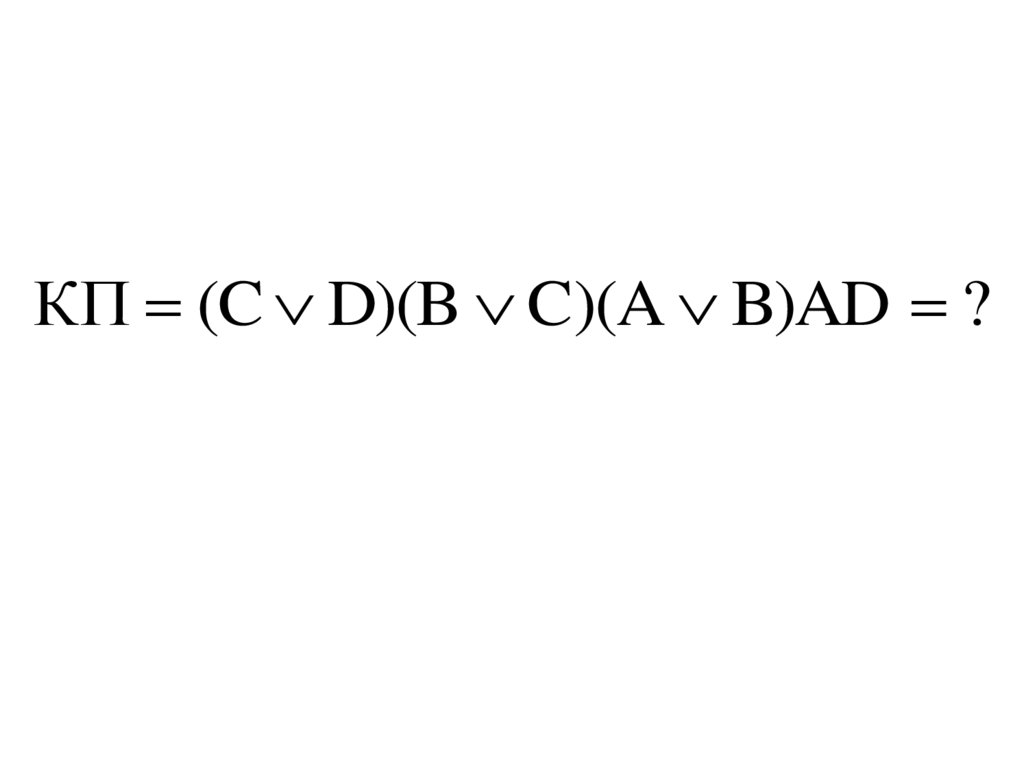
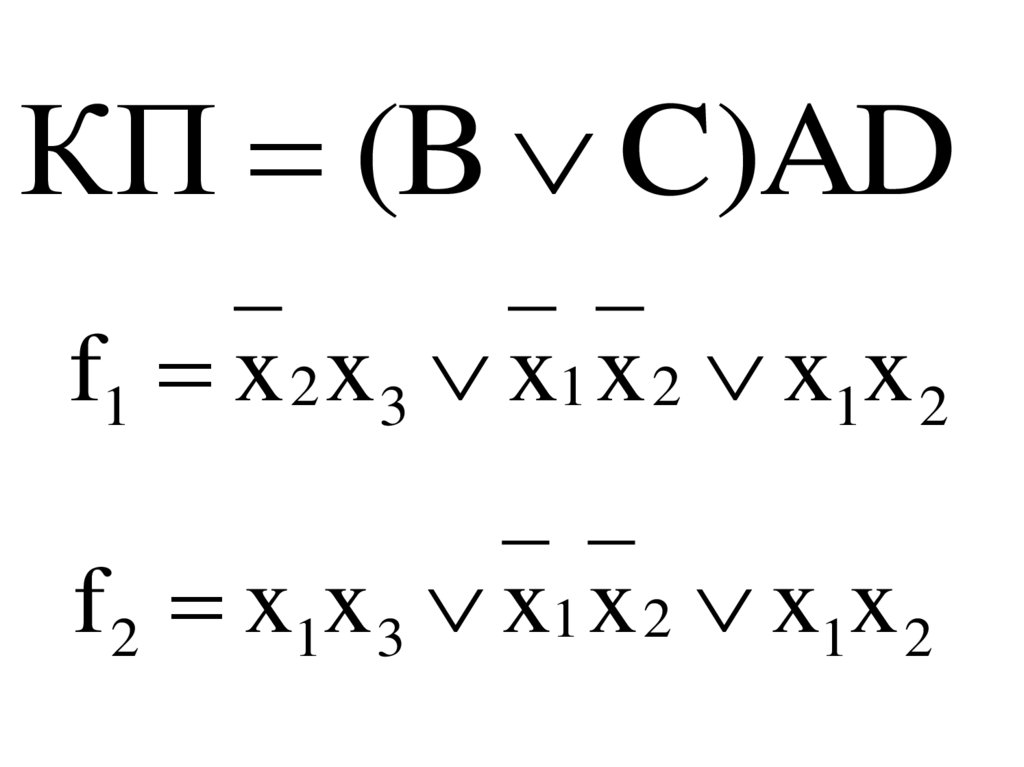










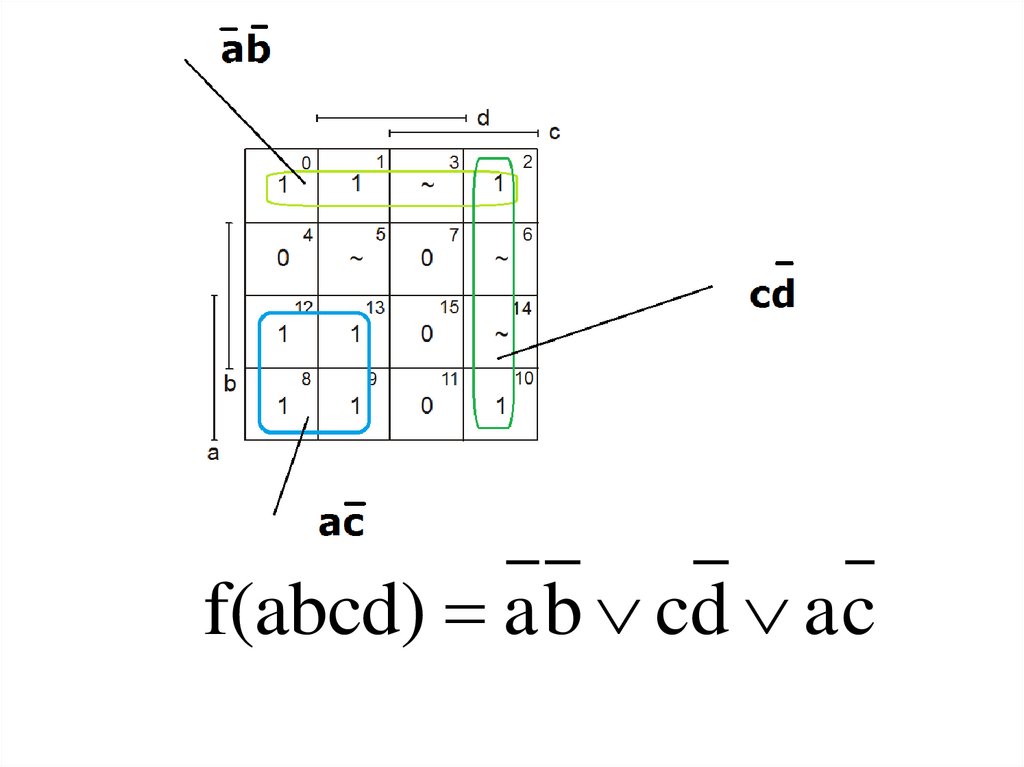
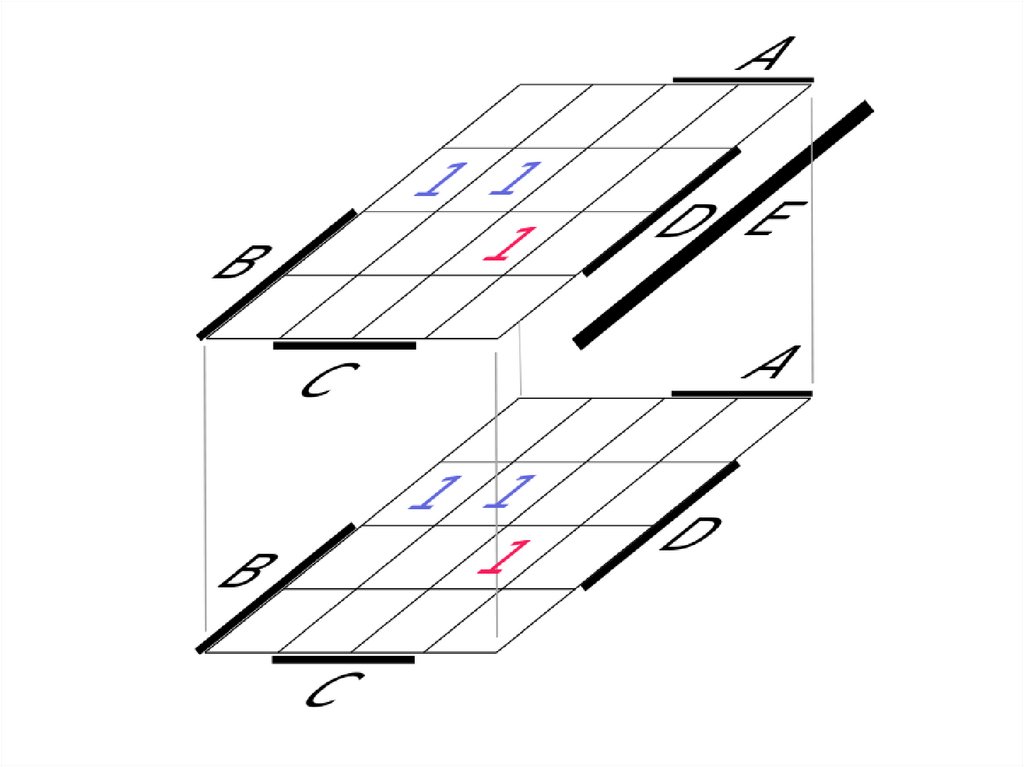

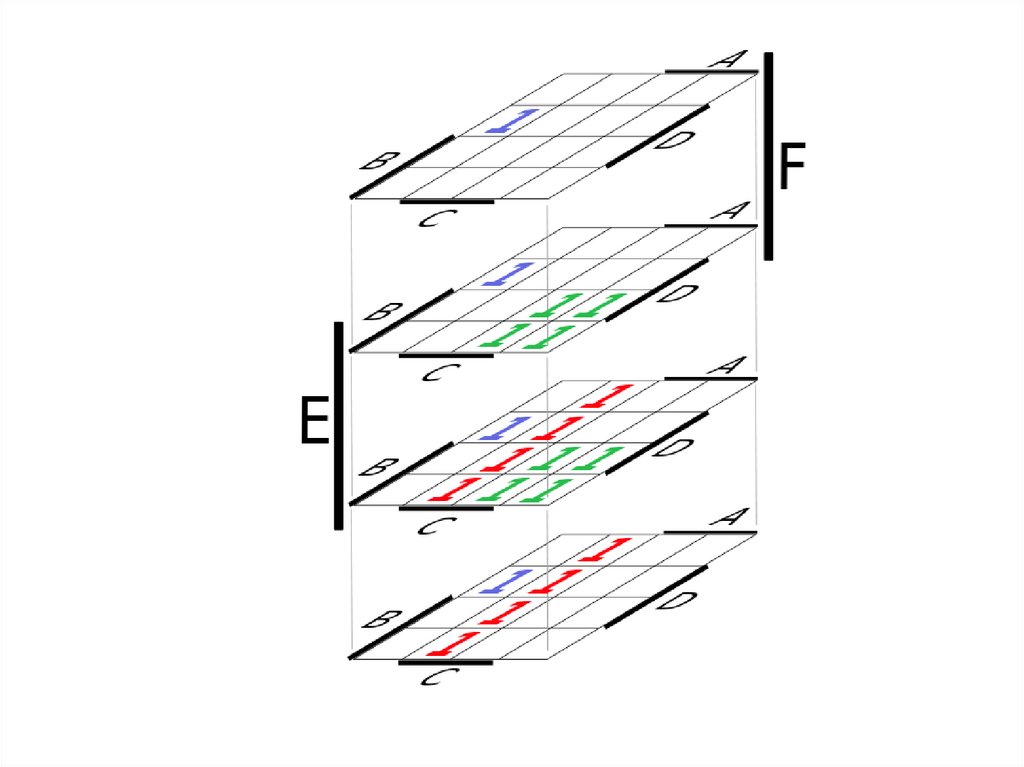
 mathematics
mathematics








