Математическая логика. Алгебра высказываний

1.

Математическая логика.
Алгебра высказываний
Джордж Буль (1815-1864г.г.)
Родился в семье рабочего. В 12 лет
знал латынь, затем овладел греческим,
французским, немецким и итальянским
языками. В 16 лет уже преподавал в
деревенской школе, а в 20 открыл
собственную школу в Линкольне.
Начиная с 1839 года Буль стал
посылать свои работы в новый
Кембриджский математический журнал.
В 1844 году молодой ученый был
награжден
медалью
Королевского
общества за вклад в математический
анализ.

2.

Вскоре Буль понял, что его алгебра вполне
применима к логике, и в 1847 году он
опубликовал памфлет «Математический анализ
логики», в котором высказал идею, что логика
более близка к математике, чем к философии.
Эта работа была чрезвычайно высоко оценена
английским математиком О. Де Морганом.
Благодаря этой работе Буль в 1849 году получил
пост профессора математики, хотя он даже не
имел университетского образования.

3. «памфлет»

Злободневная
острая
сатирическая
статья, обычно
политического
характера,
направленная
против кого-чегонибудь.
«памфлет»

4.

Буль первым показал, что существует аналогия между
алгебраическими и логическими действиями, так как и те, и
другие предполагают лишь два варианта ответов – истина
или ложь, нуль или единица.
Он придумал систему обозначений и правил, пользуясь
которыми можно было закодировать любые высказывания, а
затем манипулировать ими как обычными числами.
Булева
алгебра
располагала
тремя
основными
операциями – И, ИЛИ, НЕ, которые позволяли производить
сложение, вычитание, умножение, деление и сравнение
символов и чисел.
Таким образом, Булю удалось подробно описать двоичную
систему счисления. В своей работе «Законы мышления»
(1854 г.) Буль окончательно сформулировал основы
математической логики.
Сегодня идеи Буля используются во всех современных
цифровых устройствах.

5. Умер от воспаления легких

6.

Математическая логика – наука, изучающая
умозаключения с точки зрения их формального
строения.
Пример1.
Умозаключение1. «Все люди смертны. Сократ – человек.
Следовательно, Сократ смертен».
Умозаключение2. «Все граждане России имеют право на
образование. Сидоров – гражданин России. Следовательно
Сидоров имеет право на образование».
Эти умозаключения построены по одной и той же схеме.
Они одинаковы.
Схема: Все М – суть Р. S есть М.
Следовательно S есть Р.

7.

Высказывания
Опр. Это языковое предложение, о котором имеет смысл говорить истинно оно
или ложно.
Пример2.
«Который час?»
- не высказывание
«2*10=20»
- высказывание
«2*х=20»
- не высказывание, так как истинность зависит от чего-то
неоднозначность
Если языковое предложение содержит параметр или условие, то оно не является
высказыванием.
О высказывании всегда можно однозначно сказать: истинно оно или ложно.
Пример3.
«Москва – столица России». - высказывание
Опр. Истина и ложь называются истинностными значениями.
При этом, истина интерпретируется как 1, а ложь – как 0.

8. Высказывания обозначаются заглавными латинскими буквами A,B,C,...

Высказывания обозначаются заглавными
латинскими буквами A,B,C,...
• А: «Лондон — столица Австрии».
• B: «Число 8 больше числа 3».
• C: «Какой сегодня день недели?».
• D: «Число 13 не больше числа 7».
• E: «Число x больше 3».
• F: «2 + 3».
• G: «Луна — спутник планеты Земля».

9.

1. Отрицание
Операции над
высказываниями.
Логические операции
(связки)
Отрицанием высказывания Р является высказывание, истинное тогда и только
тогда, когда высказывание Р ложно.
Обозначение: Р или P
Аналог в языке: не верно что Р; не Р
2. Конъюнкция (связывает 2 высказывания двухместная связка)
Конъюнкцией 2-х высказываний Р и Q называется высказывание, истинное тогда
и только тогда, когда истины оба высказывания Р и Q.
Обозначение: Р Q; P Q; PQ
Аналог в языке: Р и Q (логическое умножение)
3. Дизъюнкция (связывает 2 высказывания двухместная логическая оп-ия)
Дизъюнкцией 2-х высказываний Р и Q называется высказывание, ложное тогда и
только тогда, когда ложны оба высказывания Р и Q.
Обозначение: Р Q
Аналог в языке: Р или Q

10.

4. Импликация (двухместная логическая операция)
Импликацией высказываний P и Q называется высказывание, ложное тогда и
только тогда, когда Р истинно, а Q – ложно (из истины не может следовать ложь)
Обозначение: P Q, P Q, P Q
Аналог в языке: из Р следует Q; если Р, то Q
Р – посылка импликации
Q – заключение импликации
5. Эквиваленция (двухместная логическая операция)
Эквиваленцией высказываний P и Q называется высказывание, истинное тогда и
только тогда, когда истинностные значения P и Q совпадают (либо они оба
истинны, либо оба ложны)
Обозначение:
P~Q
Аналог в языке: P эквивалентно Q

11.

Алфавит математической логики
Алфавит математической логики состоит из следующих элементов:
1. высказывательные переменные – буквы латинского алфавита, возможно с
индексами
2. логические символы:
3. символы скобок: ( )
Опр. Элементы алфавита называются символами алфавита.
Опр. Произвольная конечная последовательность символов называется словом.
Опр. Слово в алфавите логики высказываний называется формулой, если:
1. это высказывательная переменная (такая формула называется атомарной)
2. х и у формулы, то ( х), (х у), (х у), (х у), (х у) тоже формулы
3. других формул нет
Пример4. (х у) z a – слово, но не формула
Q
не формула
((х у) (z a))
Q – формула
– формула

12.

Сокращения записи формул:
1. внешние скобки можно опускать
2. считается, что отрицание относится к наикратчайшей
формуле.
Замечание.
1. Отрицание сильнее любой другой логической
операции.
2. Логическая операция конъюнкция сильнее чем любая
другая двухместная логическая операция

13.  

1. A ложно, B ложно;
2. A ложно, B истинно;
3. A истинно, B ложно;
4. A истинно, B истинно.

14.  

1. A ложно, B ложно;
2. A ложно, B истинно;
3. A истинно, B ложно;
4. A истинно, B истинно.

15.  

1. A ложно, B ложно;
2. A ложно, B истинно;
3. A истинно, B ложно;
4. A истинно, B истинно.

16.  

1. A ложно, B ложно;
2. A ложно, B истинно;
3. A истинно, B ложно;
4. A истинно, B истинно.

17. Выразите эквиваленцию через импликацию и конъюнкцию

18.

Равносильность формул
Опр. Упорядоченный набор высказывательных переменных <xi1, xi2, … , xin>
называется списком формулы А, если все переменные формулы содержатся
в этом наборе.
Пример8.
A=(x1 x2) x5
<x1 ,x2 ,x5>
B=(x2 ( x4)) ~ x8
<x2 ,x4 ,x8>
Опр. Оценкой списка переменных называется сопоставление каждой
переменной истинностного значения.
Если список содержит n переменных, то число оценок равно 2 n
Пример9.
<0, 0>, <0, 1>, <1, 0>, <1, 1> - оценки списка переменных <х1, х2>
Опр. Формулы А и В называются равносильными (эквивалентными), если на
любой оценке списка переменных они принимают одинаковые значения.
Обозначение: А ≡ В

19.

Основные равносильности
Для любых формул А, В, С справедливы следующие равносильности:
1. Коммутативность
a b≡b a
a b≡b a
2. Идемпотентность
a а≡a
a а≡a
3. Ассоциативность
a (b с) ≡ (a b) с
a (b с) ≡ (a b) с
4. Дистрибутивность
a (b с) ≡ (a b) (а с)
a (b с) ≡ (a b) (а с)
5. Законы поглощения
a ≡ а (a b)
a ≡ а (a b)

20.

6. Снятие двойного отрицания
а ≡а
7. Законы де Моргана
(a b) ≡ a b
(a b) ≡ a b
7. Расщипление
a ≡ (a b) (a b)
a ≡ (a b) (a b)
8. Взаимосвязь логических связок
а ~ b ≡ (a b) (b a) ≡ (a b)( a b)
a b ≡ a b ≡ (a b)
a b ≡ a b ≡ ( a b)
a b ≡ (a b) ≡ ( a b)

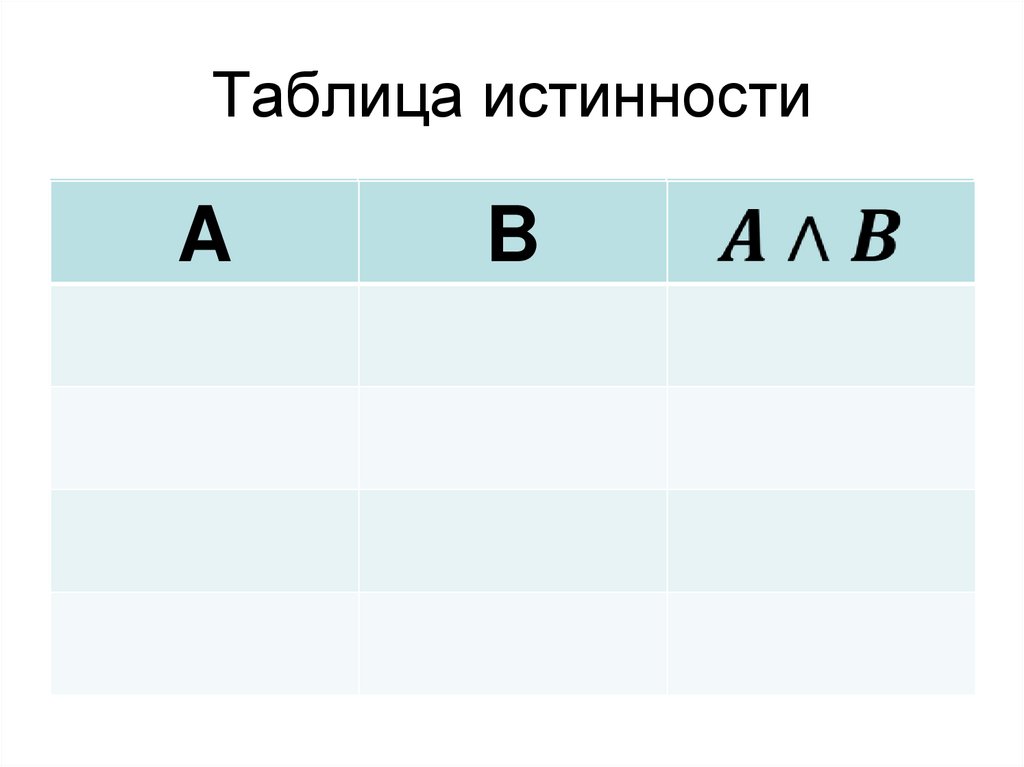
21. Таблица истинности

A
B

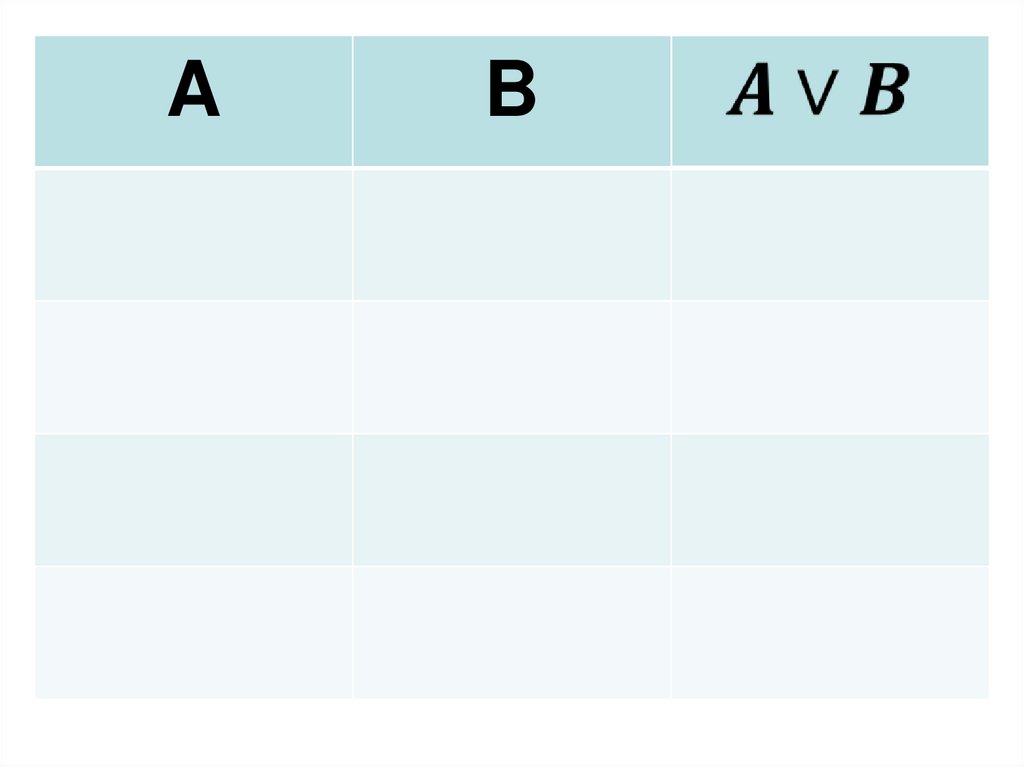
22.

A
B

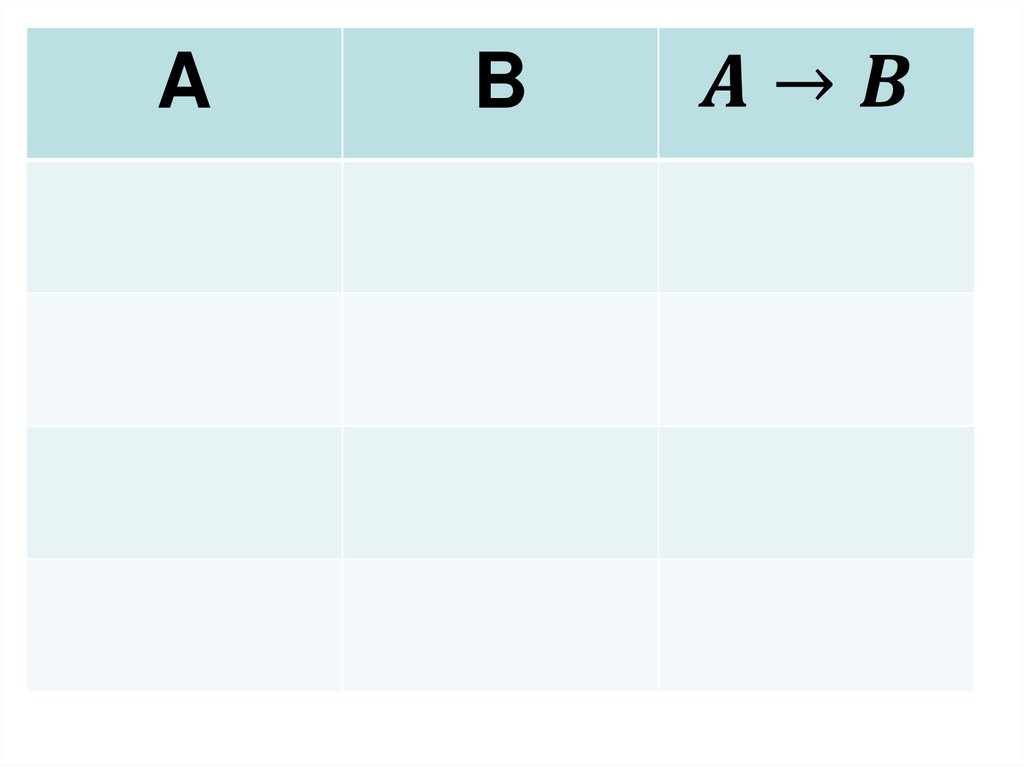
23.

A
B

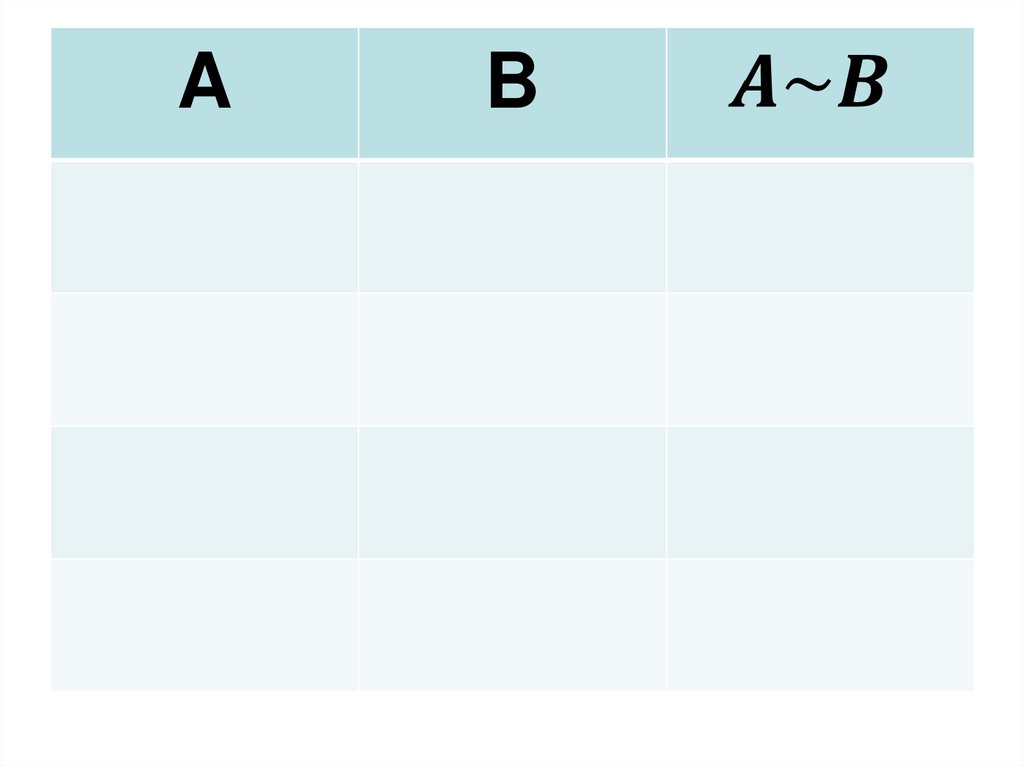
24.

A
B

25.

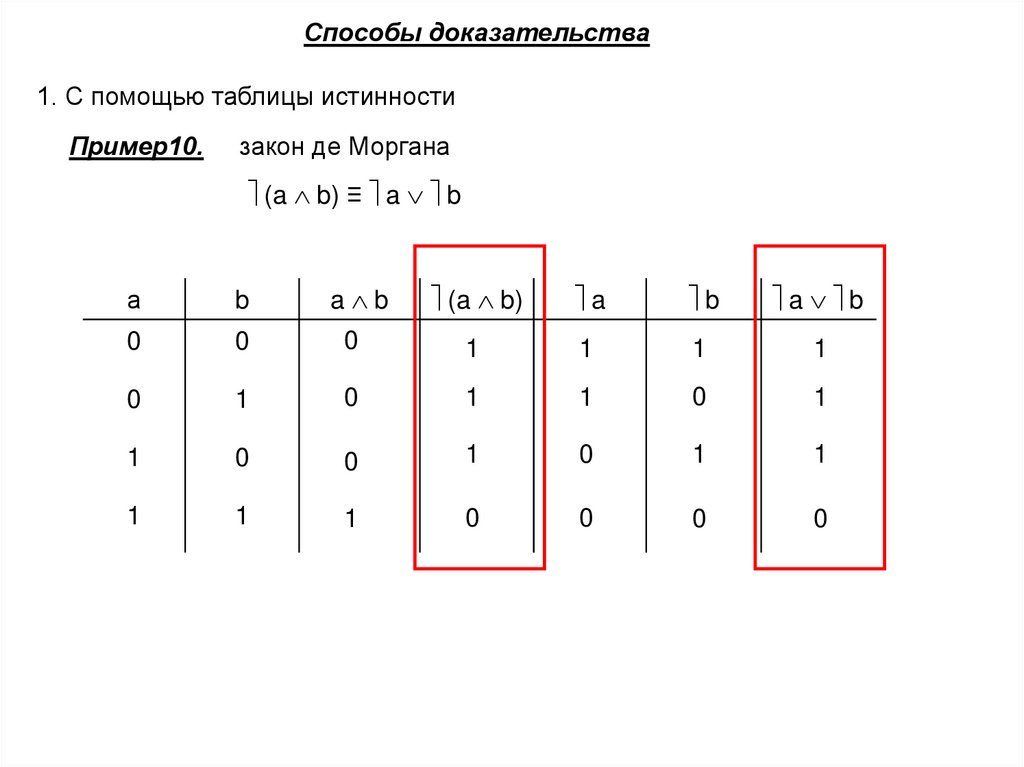
Способы доказательства
1. С помощью таблицы истинности
Пример10.
закон де Моргана
(a b) ≡ a b
а
b
a b
(a b)
a
b
a b
0
0
0
1
1
1
1
0
1
0
1
1
0
1
1
0
0
1
0
1
1
1
1
1
0
0
0
0

26.

2. Путем рассуждений
Пример11.
закон де Моргана
(a b) ≡ a b
А) Предположим, что на некоторой оценке списка переменных левая часть
формулы (a b) принимает значение ложь.
Следовательно, конъюнкция (a b) принимает значение истина.
Таким образом, значения a и b тоже истинны (по определению конъюнкции).
Тогда: a – ложь
b - ложь
Следовательно: a b - ложь
Б) Предположим, что на некоторой оценке списка переменных левая часть
формулы (a b) принимает значение истина.
Дальнейшие рассуждения аналогичны.

27.

Пусть формула А зависит от списка переменных <xi1, xi2, … , xin> .
Опр. Формула А называется тавтологией (или тождественно истинной
формулой), если на любых оценках списка переменных она принимает
значение «истина».
Опр. Формула А называется выполнимой, если на некоторых оценках списка
переменных она принимает значение «истина».
Опр. Формула А называется тождественно ложной, если на любых оценках
списка переменных она принимает значение «ложь».
Опр. Формула А называется опровержимой, если на некоторых оценках списка
переменных она принимает значение «ложь».

28.

Двойственность
Опр. Символы и называются двойственными друг к другу.
Опр. Функция F*(x1 … xn) называется двойственной к функции F(x1 … xn), если
в функции F все символы и заменены на двойственные.
Замечание. Построить функцию F*(x1 … xn), двойственную к функции F(x1 … xn),
можно только при условии, если в функции F из логических операций
присутствуют только , и .
Замечание. Двойственным к 1 является 0, а двойственным к 0 является 1.
Пример12.
F(x1, x2)=(x1 x2) x1
Пример13.
F(x1, x2)=1 (x1 x2)
F*(x1, x2)=(x1 x2) x1
a b= a b
F(x1, x2)=0 (x1 x2)
F*(x1, x2)=1 (x1 x2)
Опр. Если F*=F, то функция F называется самодвойственной.
Пример14. F(x,y,z)=xy yz xz
F*(x,y,z)=(x y) (y z) (x z)= (x y) (x y yz xz z)=
= (по дистрибутивному закону + закон поглощения)= xy (1 z) xz yz=
=xy yz xz
1

29. Спасибо за пары!