Similar presentations:
Функции и их свойства. Алгебра. 9 класс
1. Функции и их свойства.
Алгебра 9 класс.2. Что такое «функция»?
3.
12у
10
8
У=f (X)
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
4. Определение функции.
Функцией называется зависимость между двумяпеременными (У и Х) в которой каждому значению
независимой переменной (Х) соответствует
единственное значение зависимой переменной (У).
Независимую переменную называют - аргумент.
Значения зависимой переменной называют
значениями функции.
Запись У=f (X) читается: У – функция от Х.
5. Способы задания функции.
Графически.С помощью формулы.
Таблицей.
Словесный.
Рекуррентный.
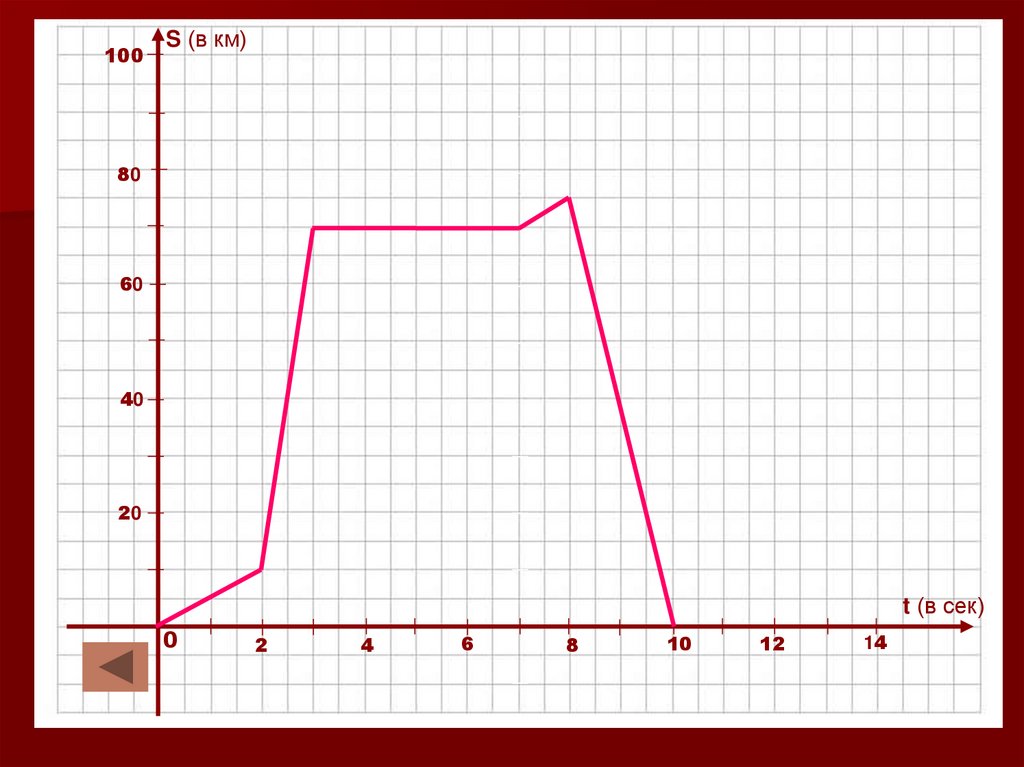
6.
100S (в км)
80
60
40
20
t (в сек)
0
2
4
6
8
10
12
14
7.
2У=х -3х+5
У=-2х+1
У=|X|-5
8.
День неделиДежурные
Понедельник
Иванова А
Вторник
Петров Д
Среда
Сидорова К
Четверг
Козлов М
Пятница
Никитин Е
Суббота
Макарова Т
9. Каждому натуральному числу поставим в соответствие его квадрат.
10. а1=3, аn+1= 2аn-1.
11. Область определения и множество значений функции.
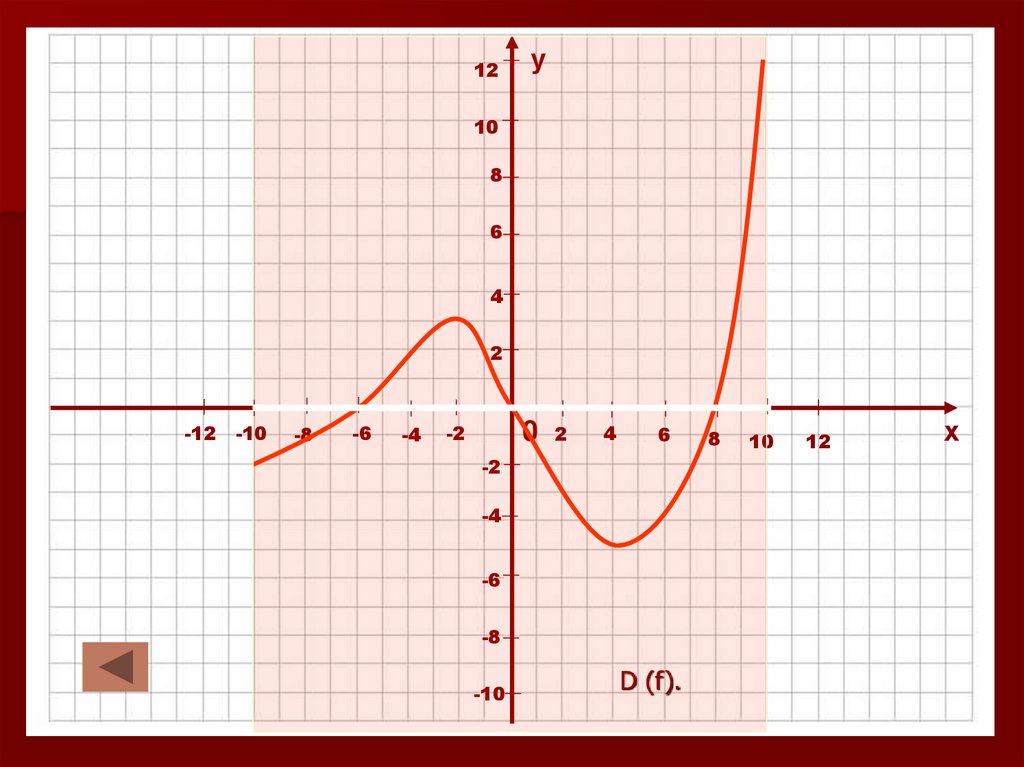
Все значения независимой переменнойобразуют область определения функции D (f).
Все значения, которые принимает
зависимая переменная, образуют область
значений функции – E (f).
12.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
4
6
-2
-4
-6
-8
-10
D (f).
8
10
12
х
13.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
4
6
8
10
х
12
-2
-4
-6
-8
-10
E (f).
14.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
4
6
8
10
х
12
-2
E (f).
-4
-6
-8
-10
D (f).
15.
Если функция задана формулой и не указана ее областьопределения, то считают, что область определения функции
состоит из всех значений аргумента, при которых формула имеет
смысл.
Укажите область определения функций:
а)
x 4
у 2
x 1
, б)
, в)
у
х 3
х 1
у 3х 5
у х 8х 1
2х 1
у 2
х 9
1
у 2
5 х 3х 2
3
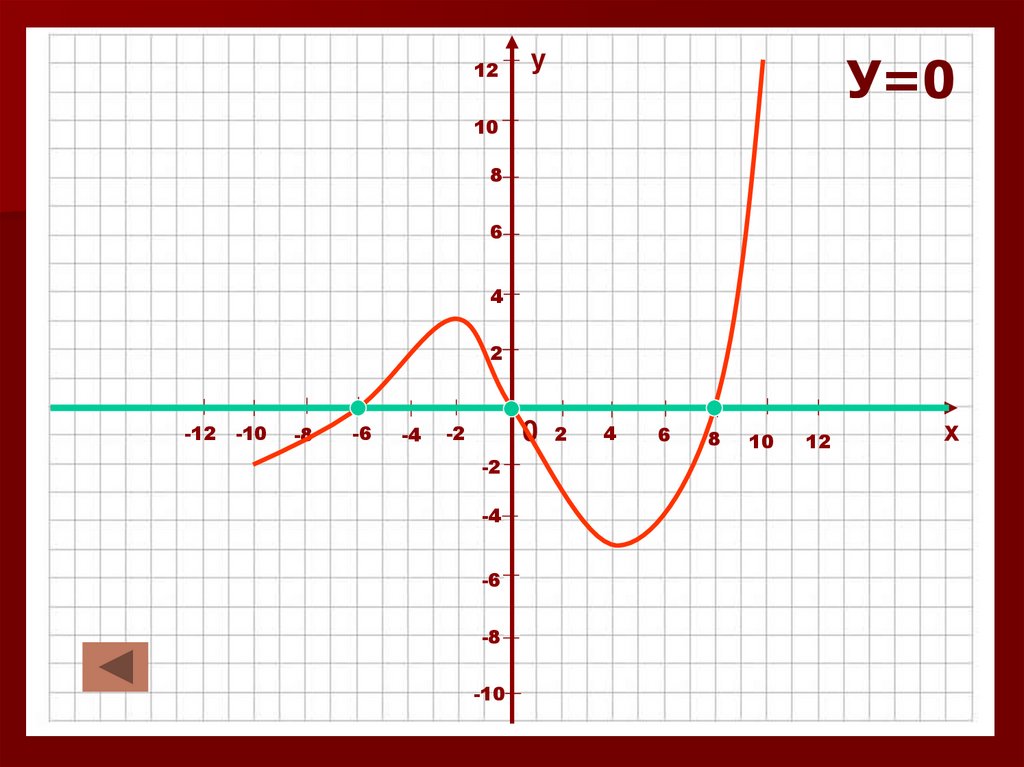
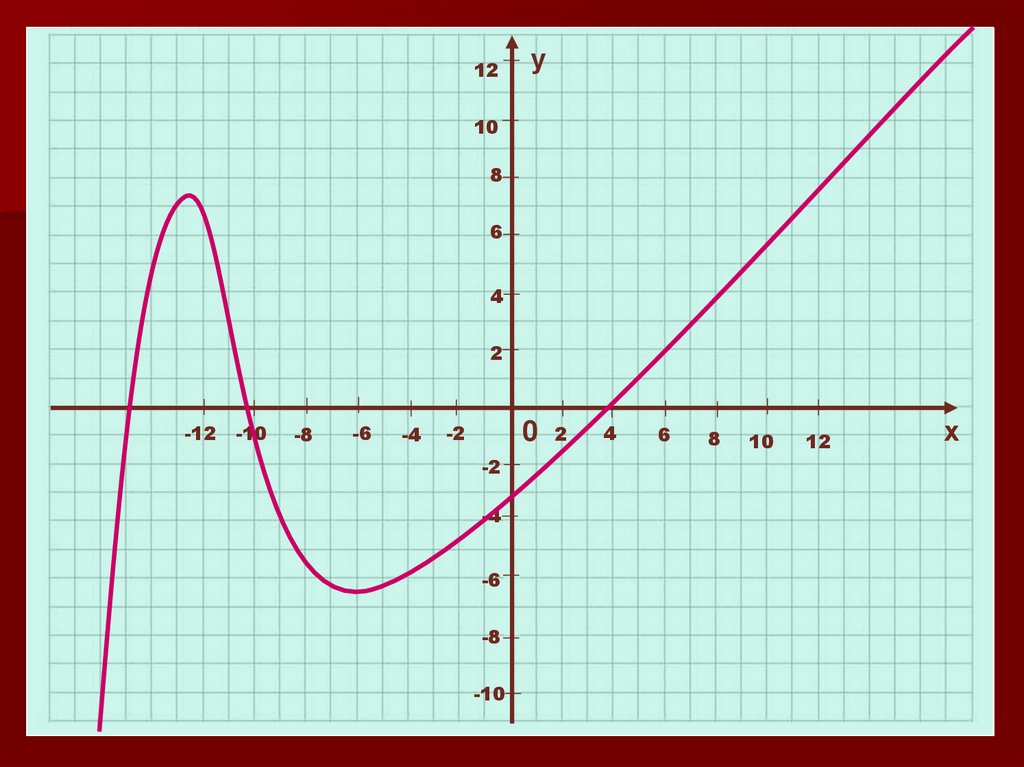
16. Промежутки знакопостоянства и нули функции.
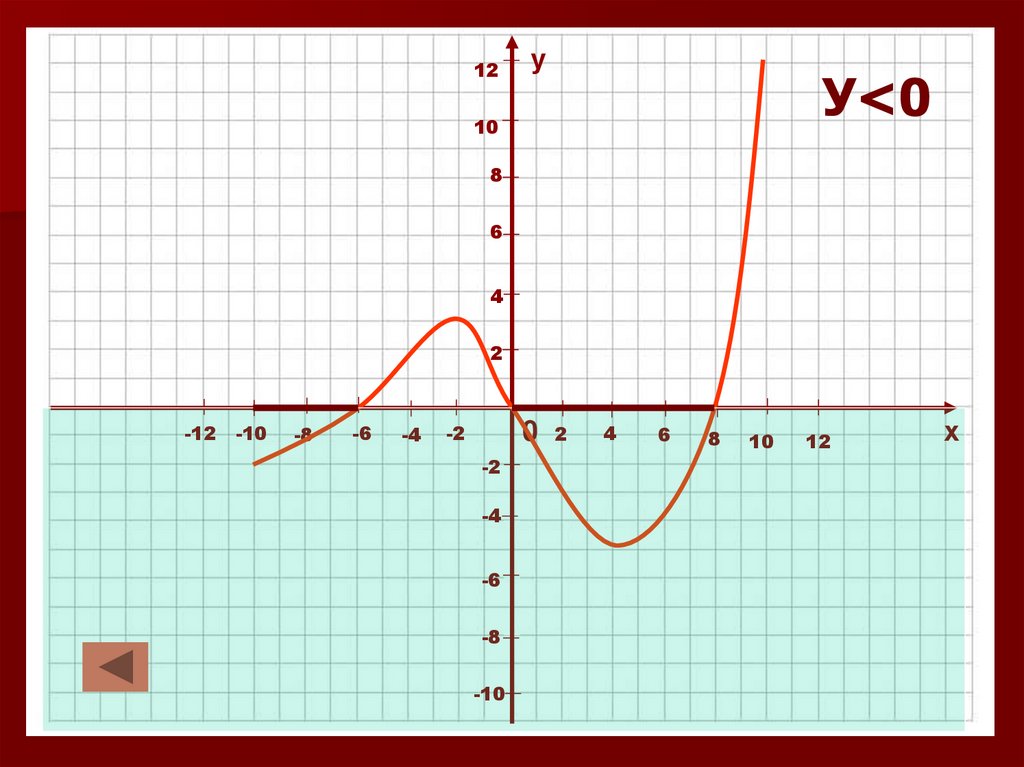
1. Значения функции положительны. У>02. Значения функции отрицательны. У<0
3. Значения функции равны нулю.
У=0
17.
12у
У>0
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
18.
12у
У<0
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
19.
12у
У=0
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
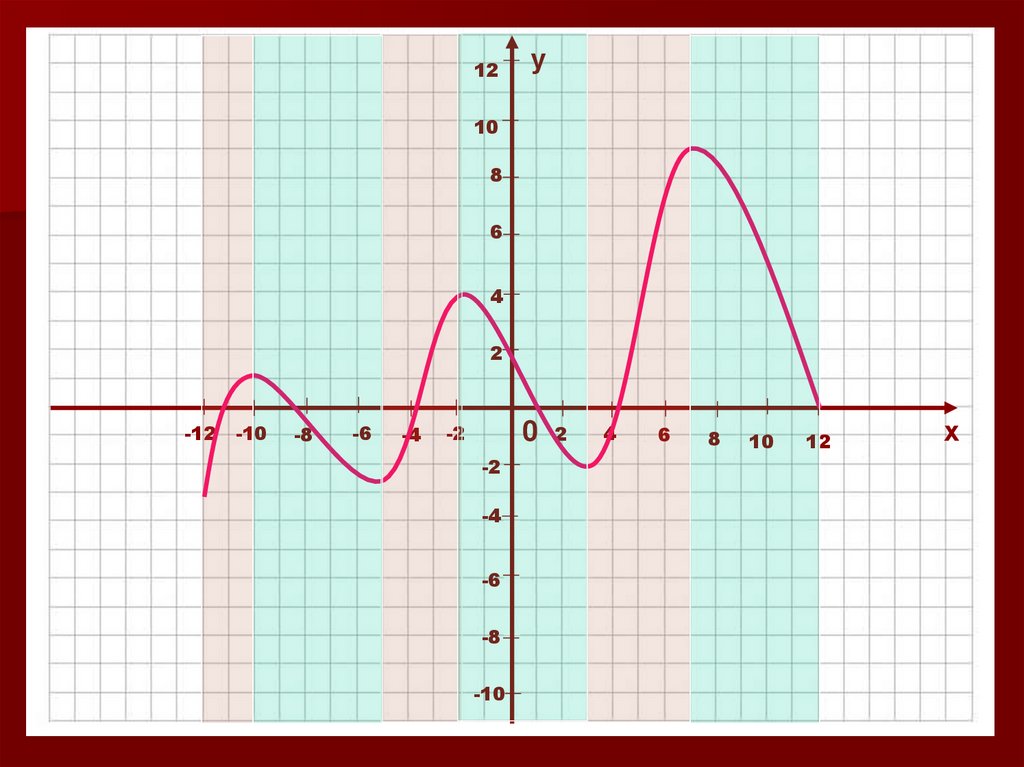
20. Монотонность функции.
Функция называется возрастающей нанекотором промежутке, если большему
значению аргумента из этого промежутка
соответствует большее значение функции.
Функция называется убывающей на
некотором промежутке, если большему
значению аргумента из этого промежутка
соответствует меньшее значение функции.
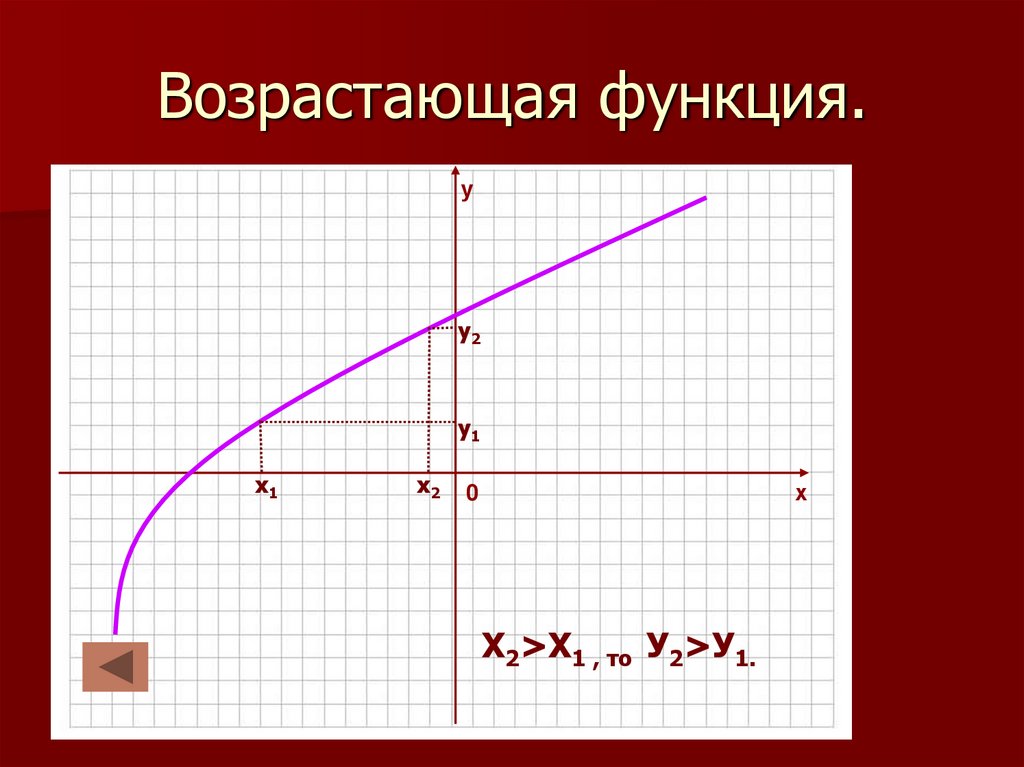
21. Возрастающая функция.
уу2
у1
х1
х2
х
0
Х2>Х1 , то У2>У1.
-10
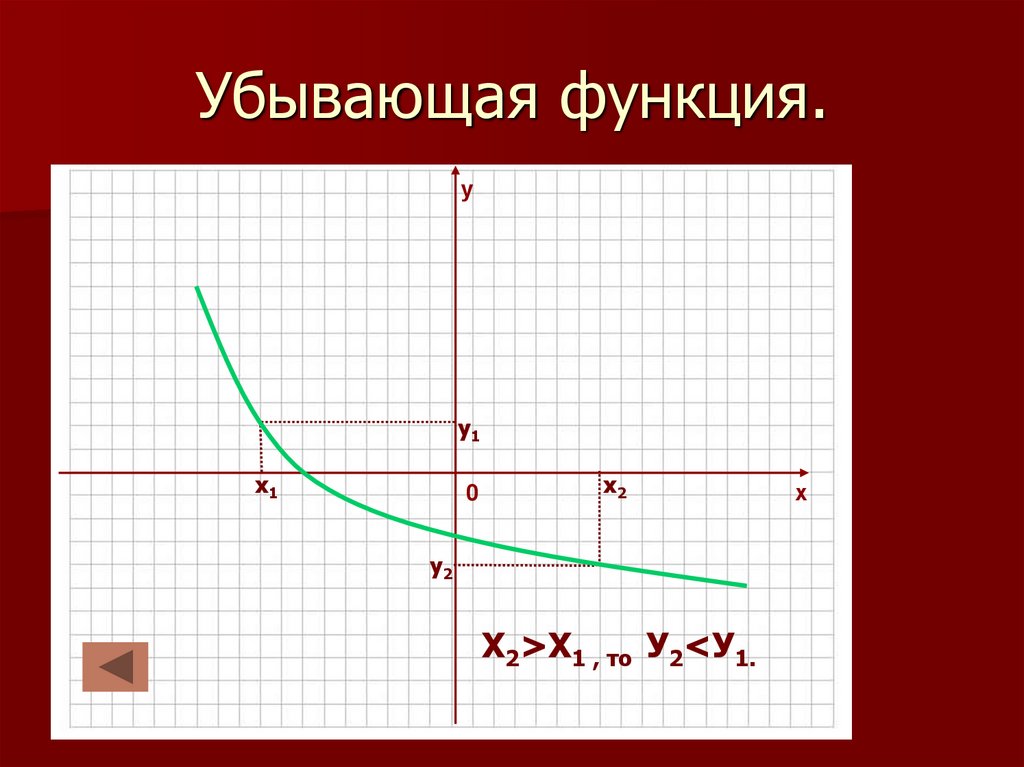
22. Убывающая функция.
уу1
х1
0
х2
х
у2
Х2>Х1 , то У2<У1.
-10
23.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
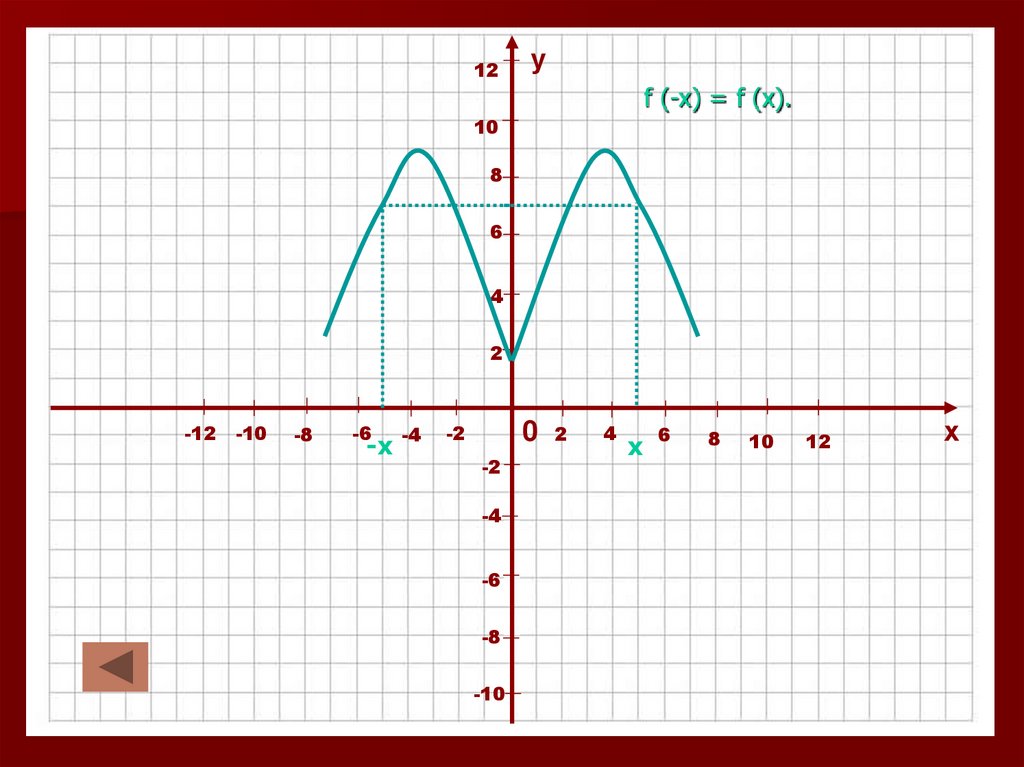
24. Четные и нечетные функции.
Функция у = f (x) называется четной, еслидля всех х из области определения функции
выполняется равенство f (-x) = f (x).
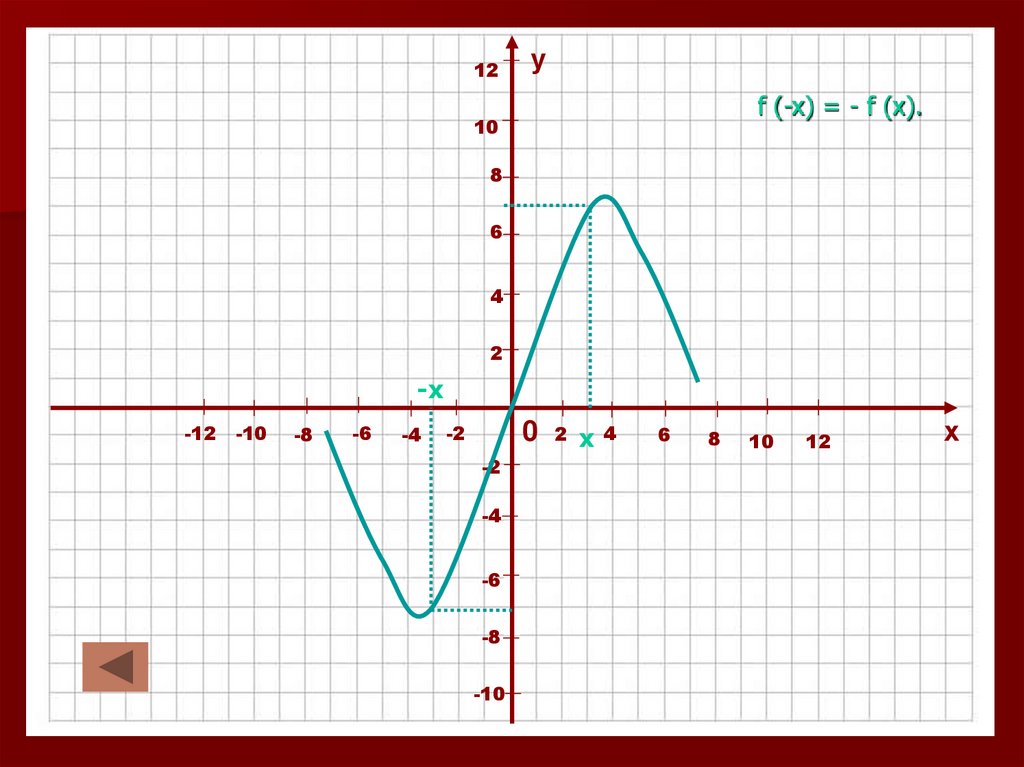
Функция у = f (x) называется нечетной, если
для всех х из области определения функции
выполняется равенство f (-x) = - f (x).
25.
12у
f (-x) = f (x).
10
8
6
4
2
-12
-10
-8
-6
-х -4
-2
0 2
-2
-4
-6
-8
-10
4
х
6
8
10
12
х
26.
12у
f (-x) = - f (x).
10
8
6
4
2
-х
-12
-10
-8
-6
-4
-2
0 2 х4
-2
-4
-6
-8
-10
6
8
10
12
х
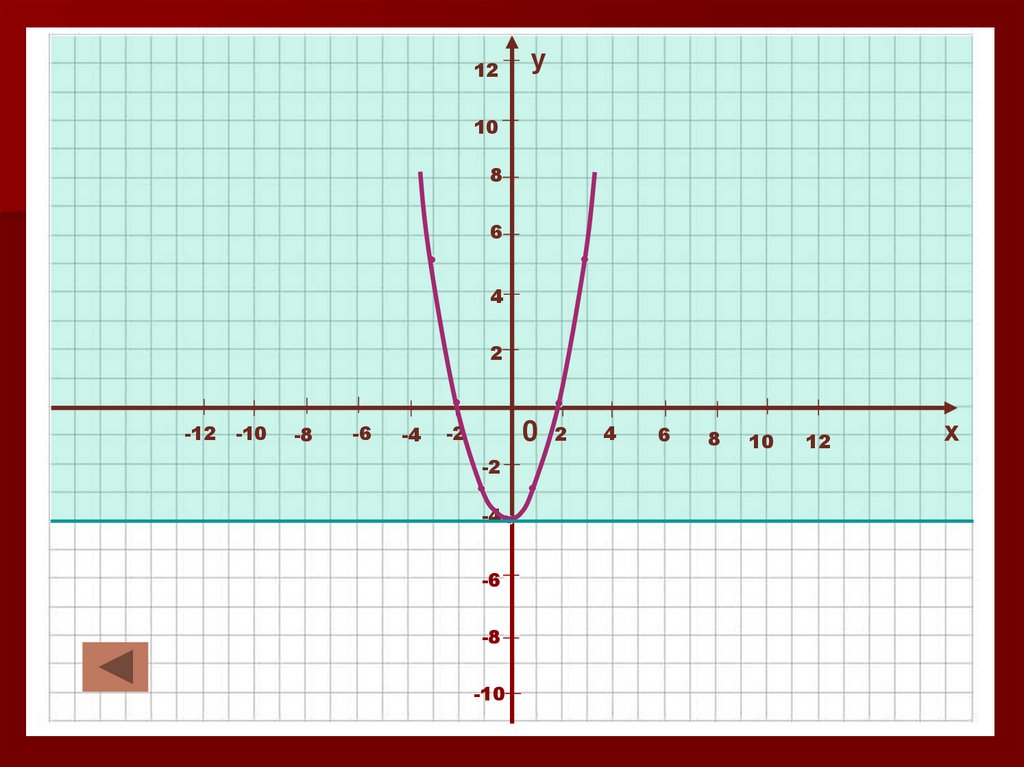
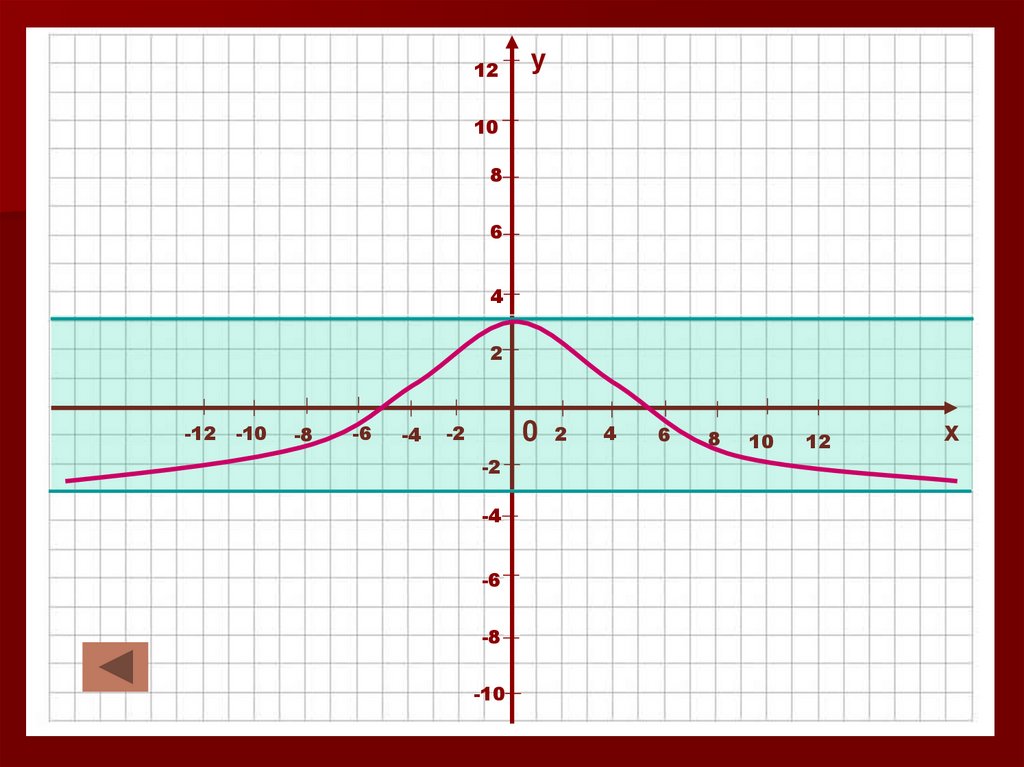
27. Ограниченность функции.
Функция y=f (x) называется ограниченнойснизу, если для любого х из области
определения функции выполняется условие
f (x)>a, где а – некоторое число.
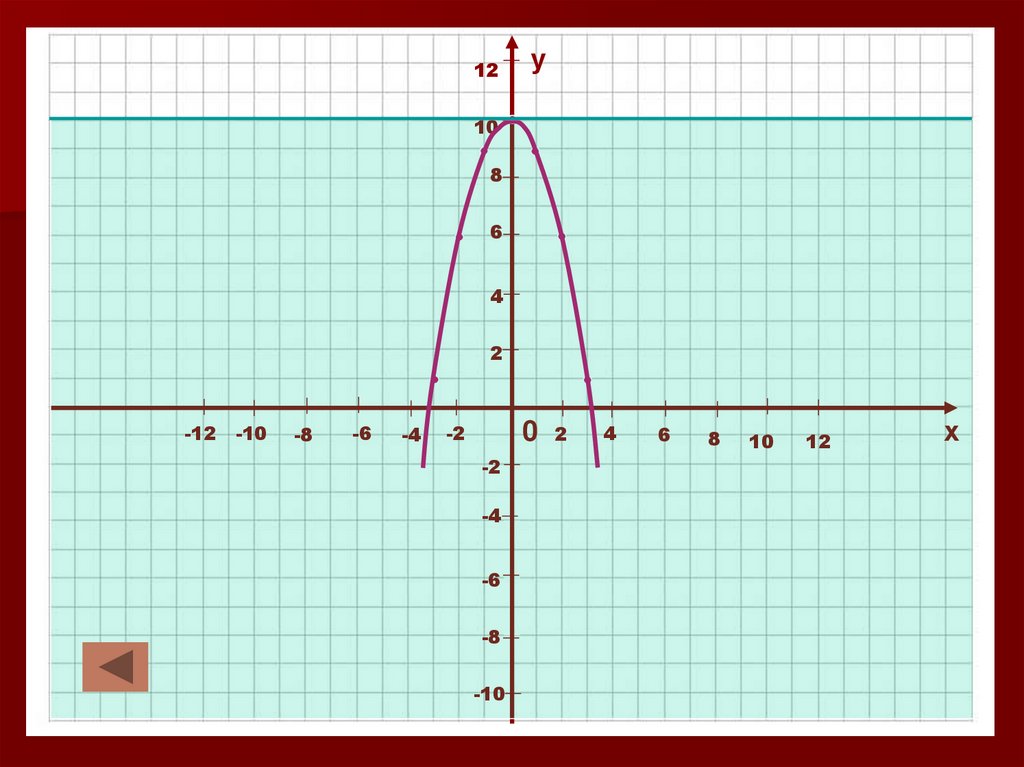
Функция y=f (x) называется ограниченной
сверху, если для любого х из области
определения функции выполняется условие
f (x)< a, где а – некоторое число.
Функция называется ограниченной, если она
ограничена и снизу, и сверху.
28.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
29.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
30.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х
31.
12у
10
8
6
4
2
-12
-10
-8
-6
-4
-2
0 2
-2
-4
-6
-8
-10
4
6
8
10
12
х








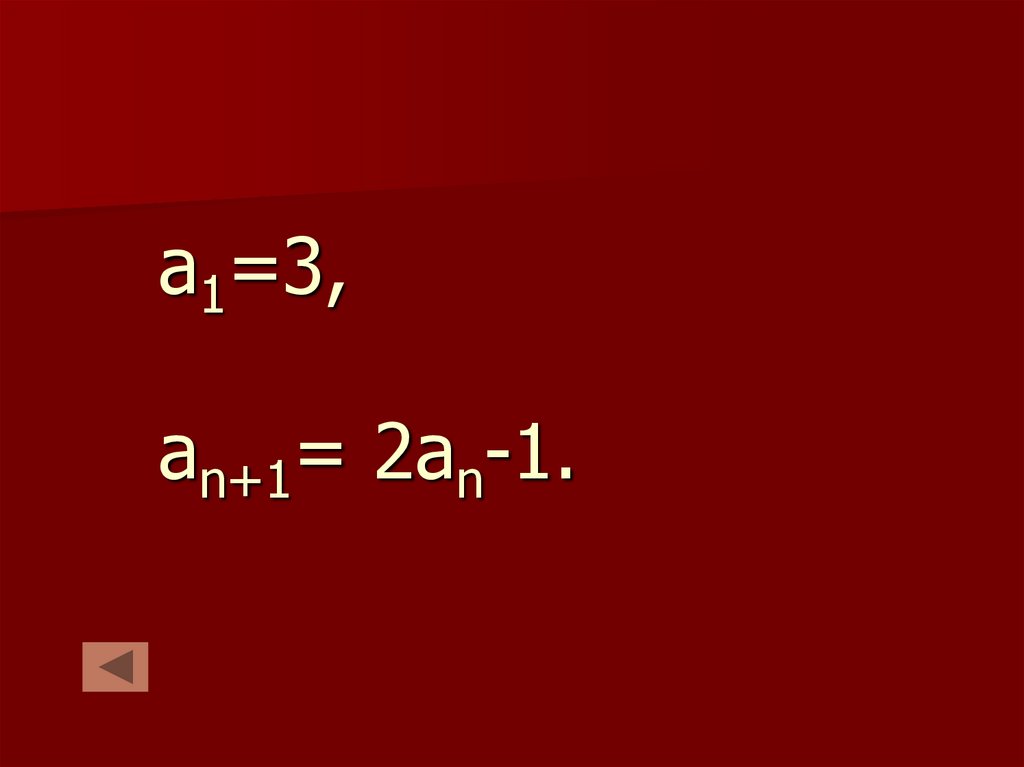









 mathematics
mathematics








