Геометрия на клетчатой бумаге

1. Геометрия на клетчатой бумаге

Кечко Татьяна Александровна
Учитель математики
МКОУ гимназия №6

2. Основные цели изучения геометрии:

Развитие у учащихся
геометрической интуиции
пространственного мышления
логического мышления
способности к конструктивногеометрической деятельности
владение символическим языком
геометрии

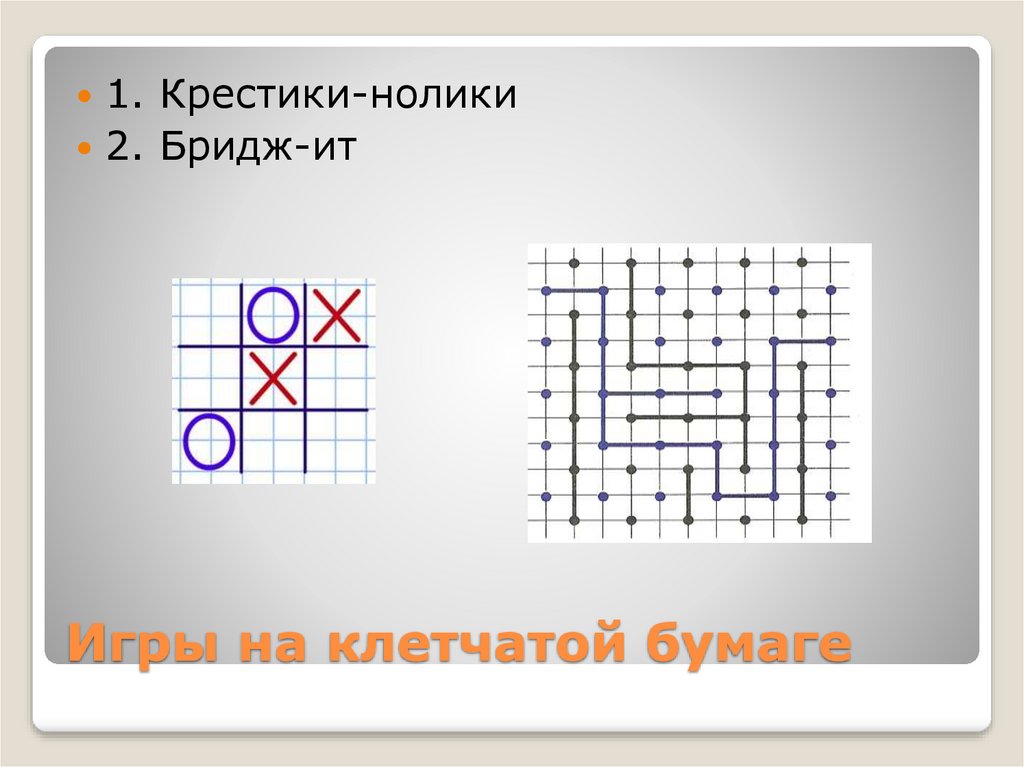
3. Игры на клетчатой бумаге

1. Крестики-нолики
2. Бридж-ит
Игры на клетчатой бумаге

4. Расстояния в «клетчатом» городе

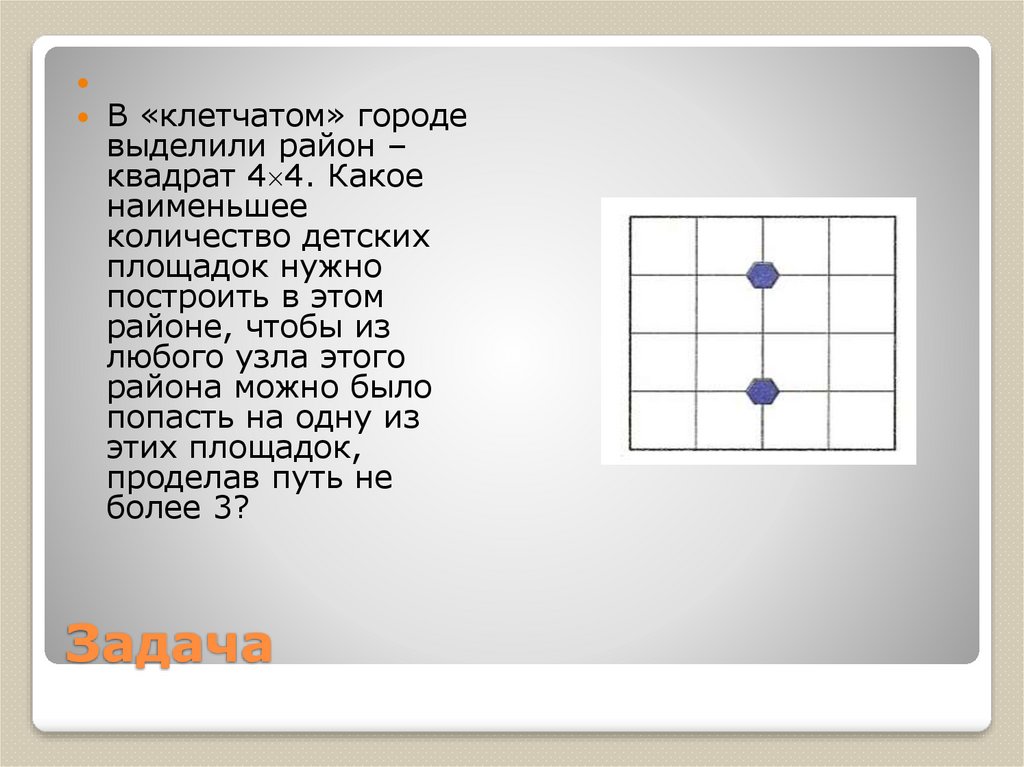
5. Задача

В «клетчатом» городе
выделили район –
квадрат 4 4. Какое
наименьшее
количество детских
площадок нужно
построить в этом
районе, чтобы из
любого узла этого
района можно было
попасть на одну из
этих площадок,
проделав путь не
более 3?
Задача

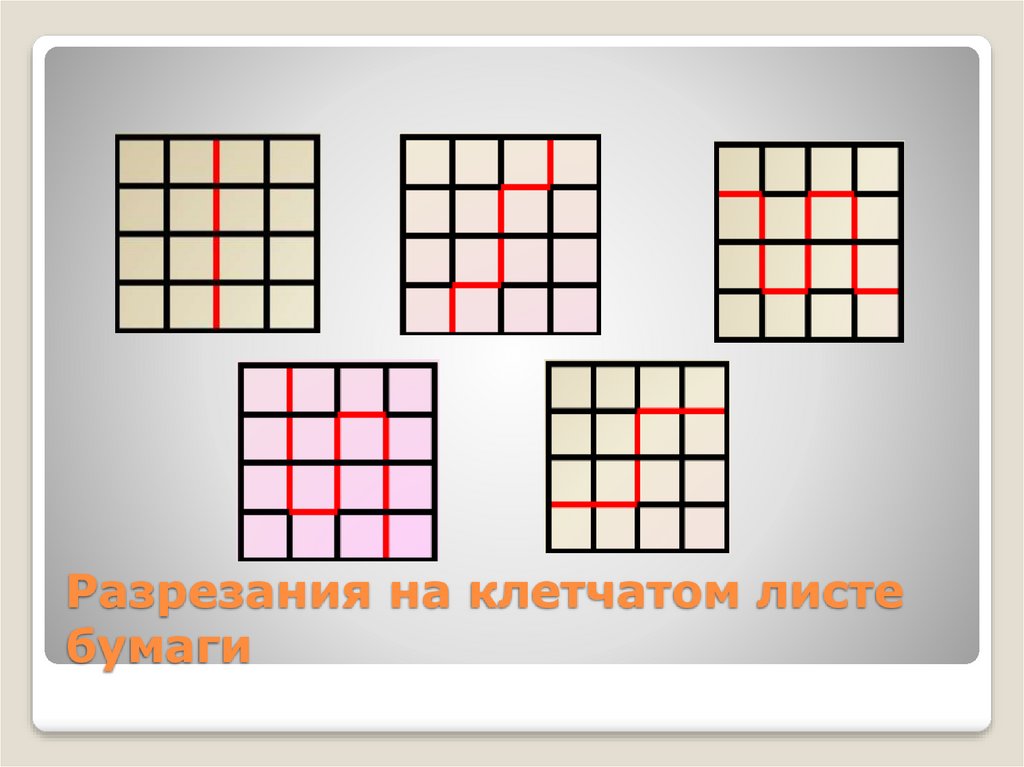
6. Разрезания на клетчатом листе бумаги

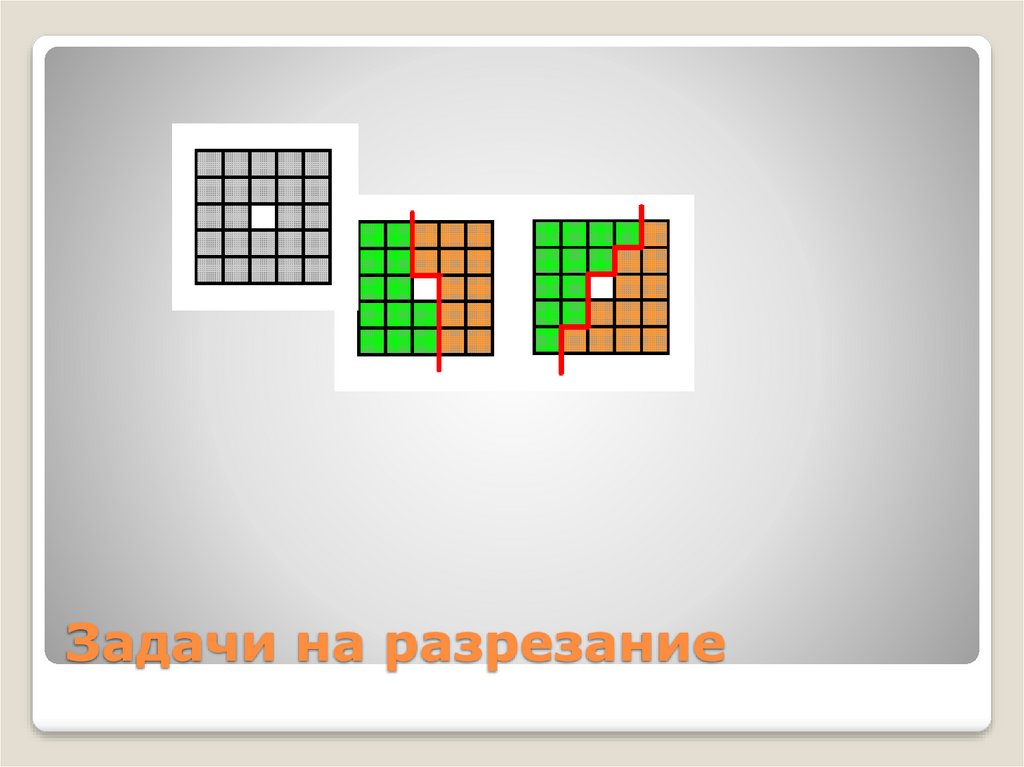
7. Задачи на разрезание

8. Задача №2

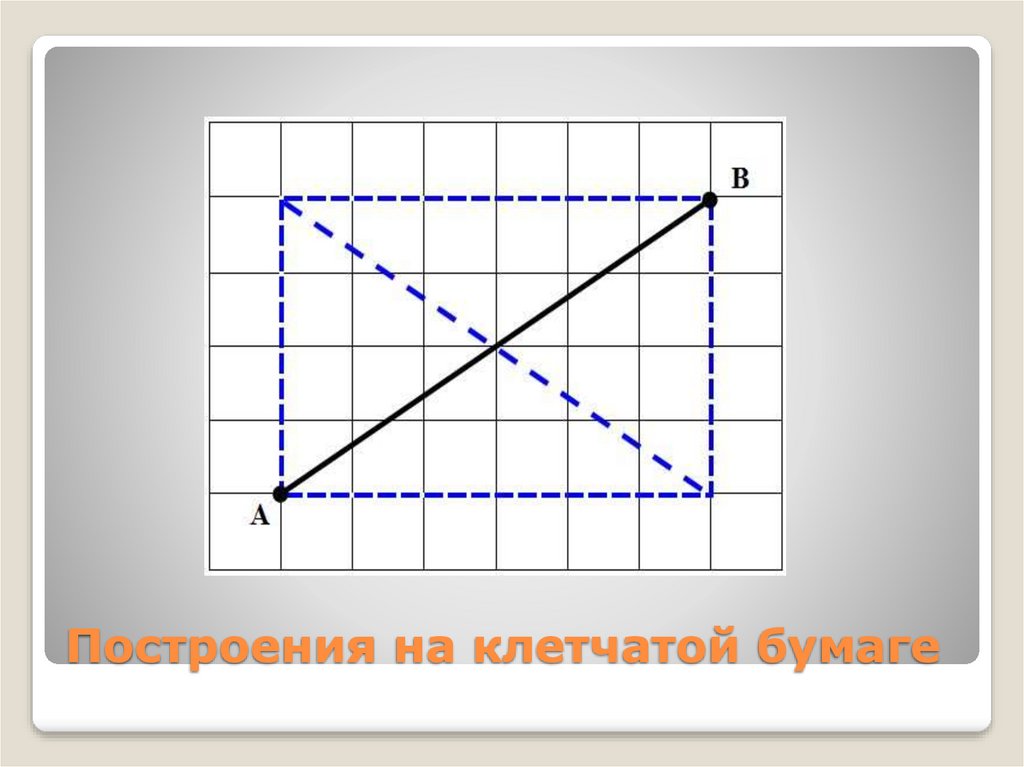
9. Построения на клетчатой бумаге

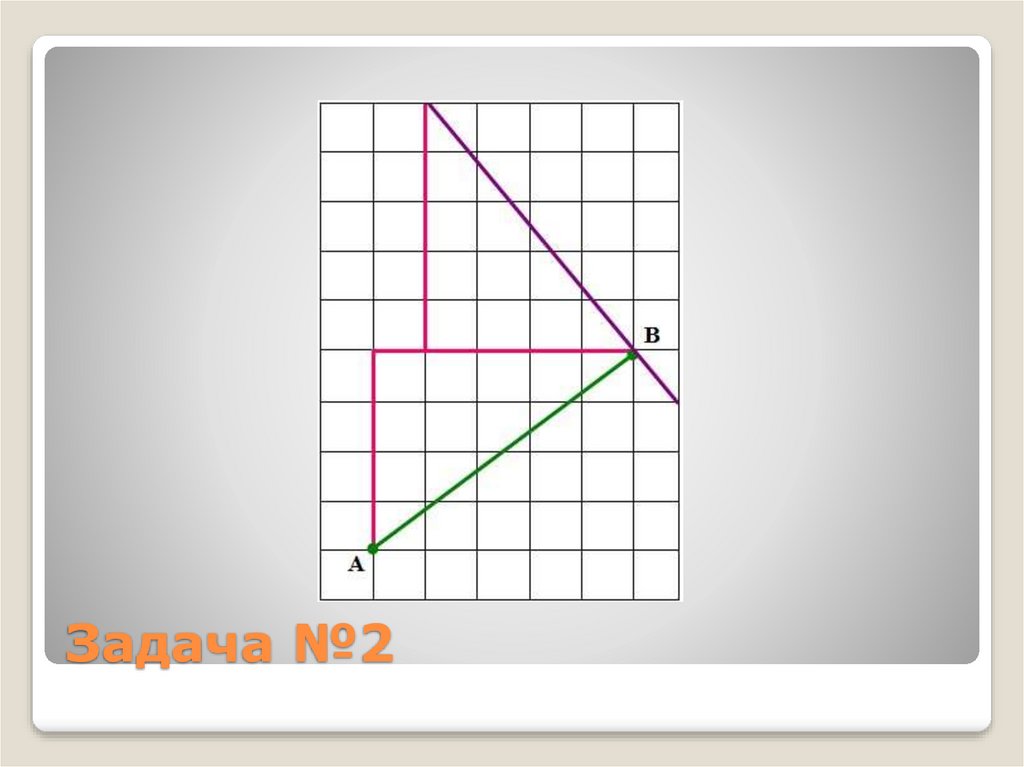
10. Задача №2

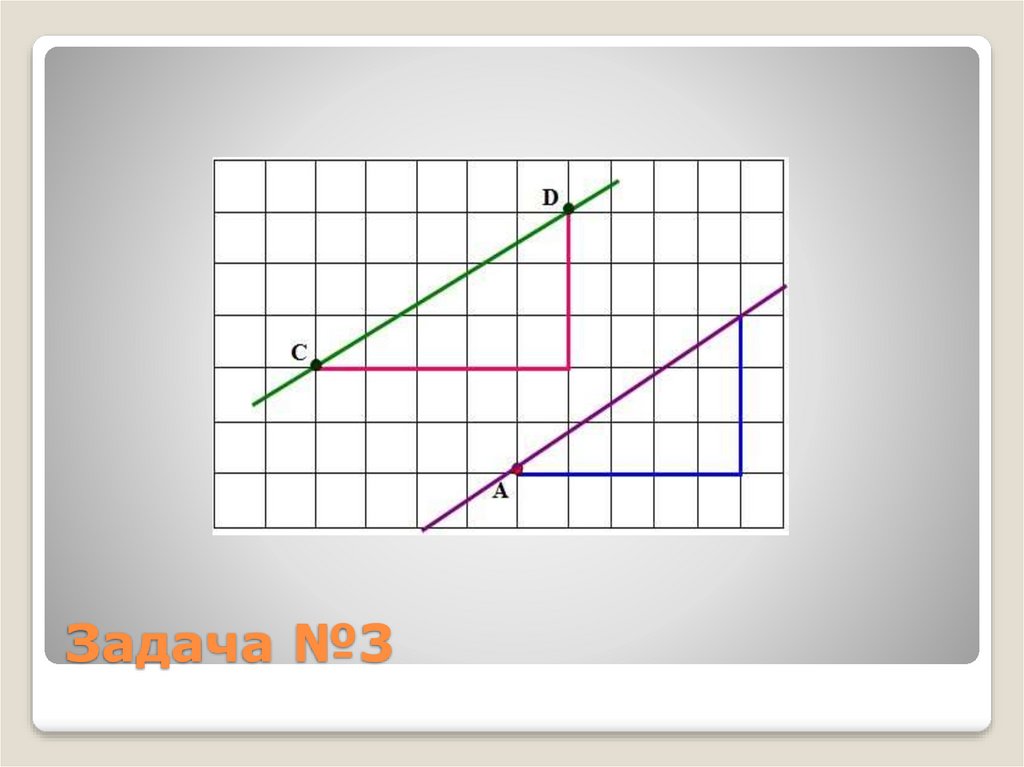
11. Задача №3

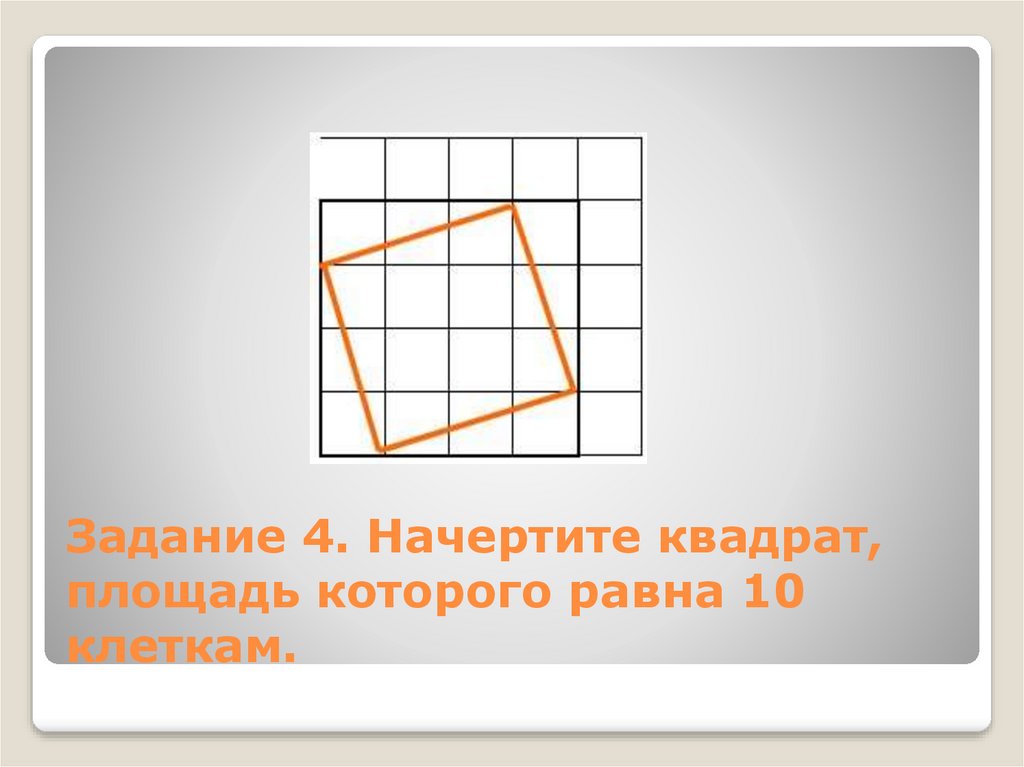
12. Задание 4. Начертите квадрат, площадь которого равна 10 клеткам.

Задание 4. Начертите квадрат,
площадь которого равна 10
клеткам.

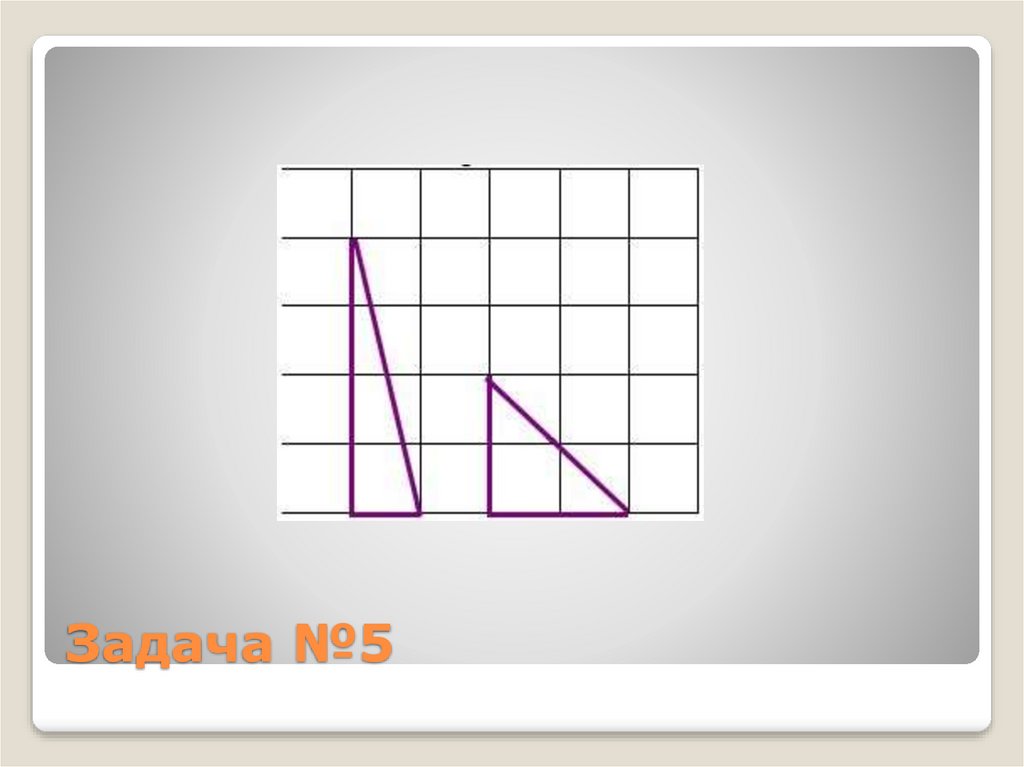
13. Задача №5

14. Задача №6

15. Нахождение площади многоугольника

16. Формула Пика

Площадь многоугольника с
целочисленными вершинами равна сумме:
В+ Г/2 −1,
где В количество целочисленных точек внутри
многоугольника, а Г количество целочисленных
точек на границе многоугольника
В=7, Г=8,
В+ Г/2 −1= 10
Формула Пика

17. Вычисление площади

M = 24 (обозначены красным)
N = 25 (обозначены синим)
Вычисление площади

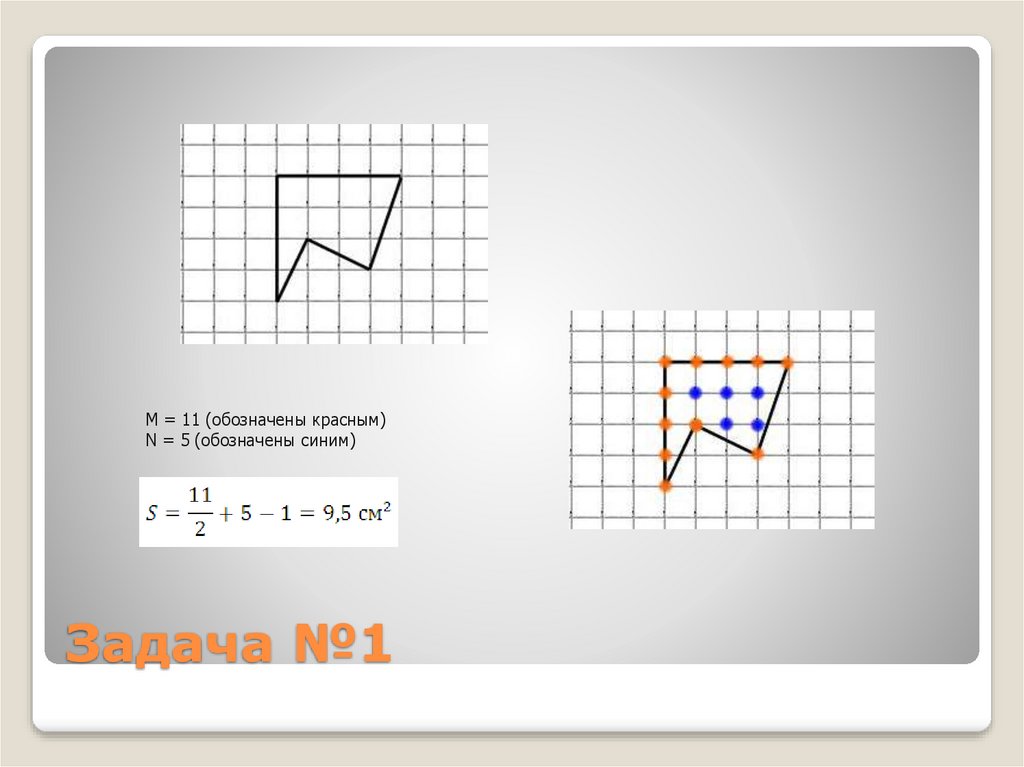
18. Задача №1

M = 11 (обозначены красным)
N = 5 (обозначены синим)
Задача №1

19. Задача №1а

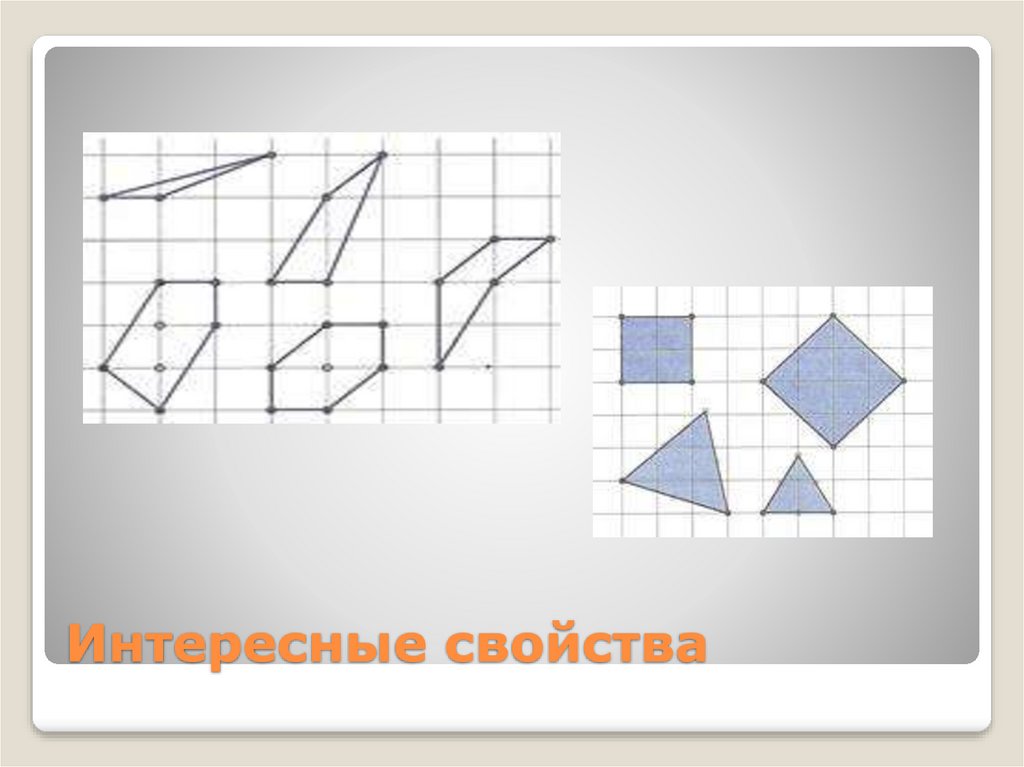
20. Интересные свойства

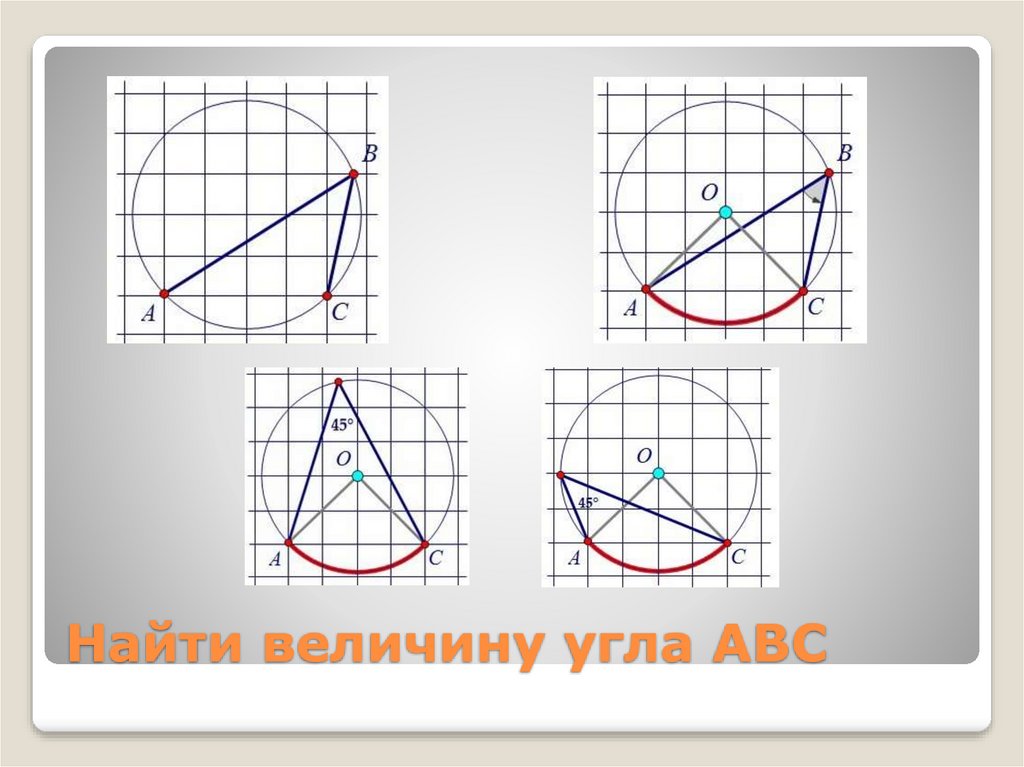
21. Найти величину угла АВС

22.

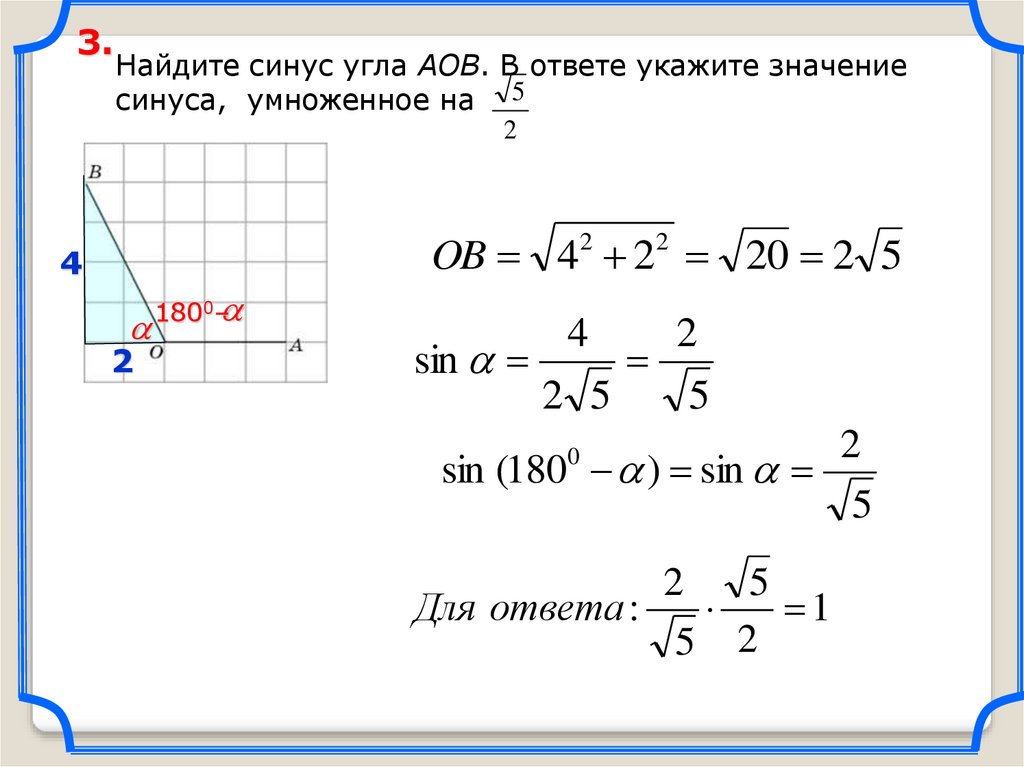
3.
Найдите синус угла AOB. В ответе укажите значение
синуса, умноженное на 5
2
OB 42 22 20 2 5
4
2
1800–
4
2
sin
2 5
5
2
sin (180 ) sin
5
0
2
5
Для ответа :
1
5 2

23.

«Математика через игры ума
развивает
разные
виды
мышления, и ребёнок становится
умнее».
Илья Иосифович Брук

24. Спасибо за внимание