Неопределенный интеграл

1.

.

2.

Евдокс Книдский
ок. 408 — ок. 355 год до н. э.

3.

Неопределенным интегралом от
непрерывной функции f(x) на
интервале (a; b) называют
совокупность первообразных
функции.
f
(
x
)
dx
F
(
x
)
c
Где С – произвольная постоянная (const).

4.

5.

Свойства интеграла
(
f
(
x
)
g
(
x
)
)
dx
f ( x)dx g ( x)dx
C
f
(
x
)
dx
Cf
(
x
)
dx

6. Основные методы интегрирования

1.Табличный.
2.Сведение к табличному
преобразованием подынтегрального
выражения в сумму или разность.
3.Интегрирование с помощью замены
переменной (подстановкой).
4.Интегрирование по частям.

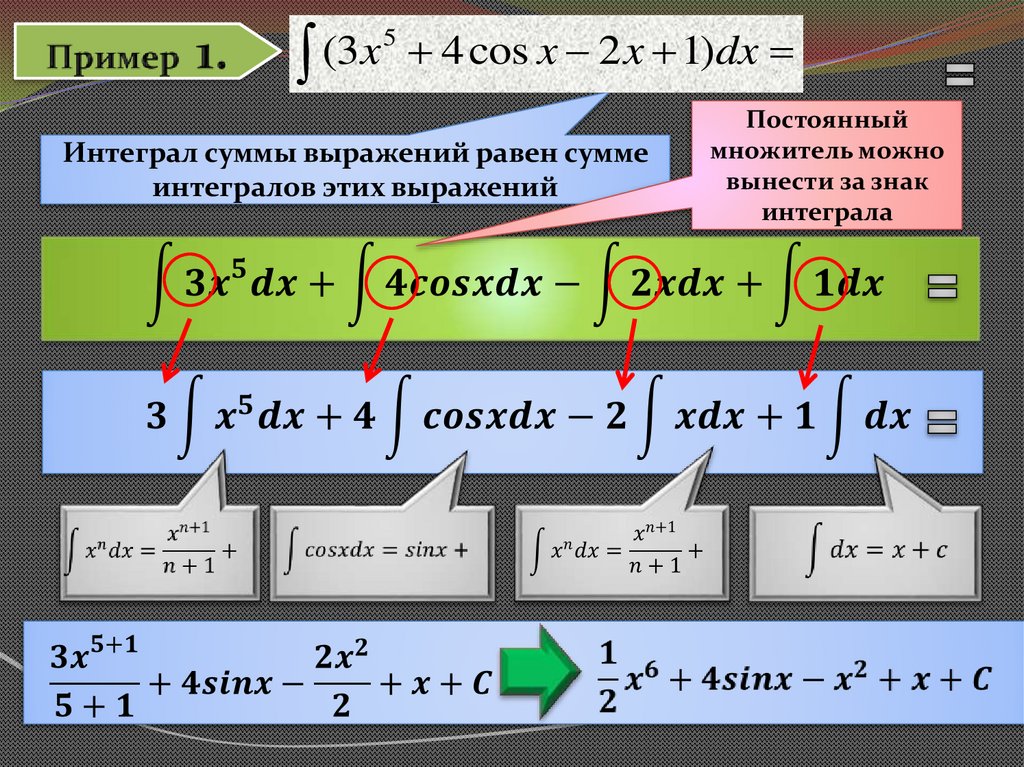
7.

5
(
3
x
4 cos x 2 x 1)dx
Интеграл суммы выражений равен сумме
интегралов этих выражений
Постоянный
множитель можно
вынести за знак
интеграла

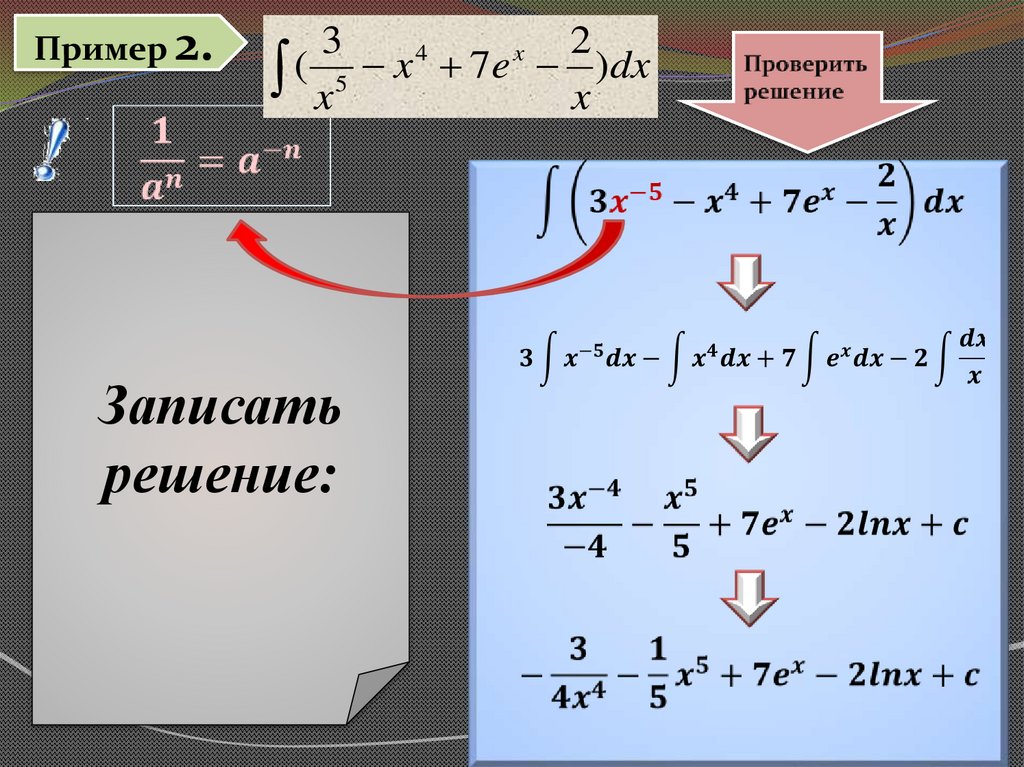
8.

Пример 2.
3
2
4
x
( x5 x 7e x )dx
Записать
решение:

9.

sin( 6 x 2)dx
Введем новую переменную и
выразим дифференциалы:
Записать
решение:

10.

Пример 5.
3 6 x dx
Записать
решение:
Проверить
решение