Основы динамики

1.

Лекция 2. Основы динамики. Законы Ньютона.
Законы Ньютона — три важнейших закона классической механики,
которые позволяют записать уравнения движения для
любой механической системы, если известны силы,
действующие на составляющие её тела.
*) Придание законам Ньютона статуса аксиом — лишь
один из методологических подходов, принятый в средней
школе, а также в большинстве вузовских курсов общей
физики.
**) Существует, например, более фундаментальная –
«теоретическая механика», в которой эти законы выводятся
из принципа «наименьшего действия».
(мы не изучаем, просто для понимания)
-------------------------------------------------------------------------------------------------------**) Впервые в полной мере сформулированы Исааком Ньютоном в
книге «Математические начала натуральной философии» (1687
год)
1

2.

Лекция 2. Основы динамики. Законы Ньютона.
Основные определения
Масса – физическая величина, определяющая инерционные и
гравитационные свойства физических тел.
•) вводят инертную и гравитационную массы.
Их эквивалентность – эмпирический факт.
•) КГ – единица измерения в СИ (в других, например: г – в системе СГС)
•) Вес не равен Массе.
Сила – векторная величина, мера механического воздействия на тело со
стороны других тел и полей, в результате которого тело приобретает ускорение
или изменяет форму и размеры.
•) [ Н ] – (Ньютон) – единица измерения в СИ
•) Введены понятия «Поле» и «Деформация». Их мы узнаем позже. Опережающе введение
понятий при изучении предмета физика, к сожалению, неизбежность
Импульс (количество движения) – векторная величина,
произведение массы тела на скорость его перемещения относительно системы
отсчета
2

3.

Лекция 2. Основы динамики. Законы Ньютона.
Первый закон Ньютона (Закон инерции)
Существуют такие системы отсчёта,
называемые инерциальными, относительно
которых материальные точки, когда на них не
действуют никакие силы (или действуют силы взаимно
уравновешенные), находятся в состоянии покоя
или равномерного прямолинейного движения.
(!) ВАЖНО:
•Не всякая система инерциальная, более того, такую систему очень трудно
найти в реальном мире.
•Проявления, связанные с неинерциальностью системы могут быть
пренебрежимо малы. Поэтому систему отсчета связанные, например, с земной
поверхностью или с Солнцем с большой точностью можно считать
инерциальными.
•Если существует инерциальная система отсчета, то другая система отсчета,
движущаяся прямолинейно и равномерно – тоже инерциальная. И, наоборот,
движущаяся с ускорением – неинерциальная.
3

4.

Лекция 2. Основы динамики. Законы Ньютона.
Второй закон Ньютона
В терминах силы: («формулировка для практики»)
В инерциальной системе отсчёта ускорение, которое получает
материальная точка с постоянной массой, прямо пропорционально
равнодействующей всех приложенных к ней сил и обратно
пропорционально её массе.
В терминах импульса: («формулировка для теории»)
В инерциальной системе отсчета скорость изменения импульса
материальной точки равна равнодействующей всех приложенных к
ней внешних сил.
Самая общая формулировка
«Уравнения движения»:
(!) Важно:
•) 2й З.Н. работает только ИСО!
(к неинерциальным СО необходим особый подход)
•) В 2м З.Н. заложен (или из него вытекает) принцип независимости разных
воздействий (сил) на тело со стороны др.тел или полей.
4

5.

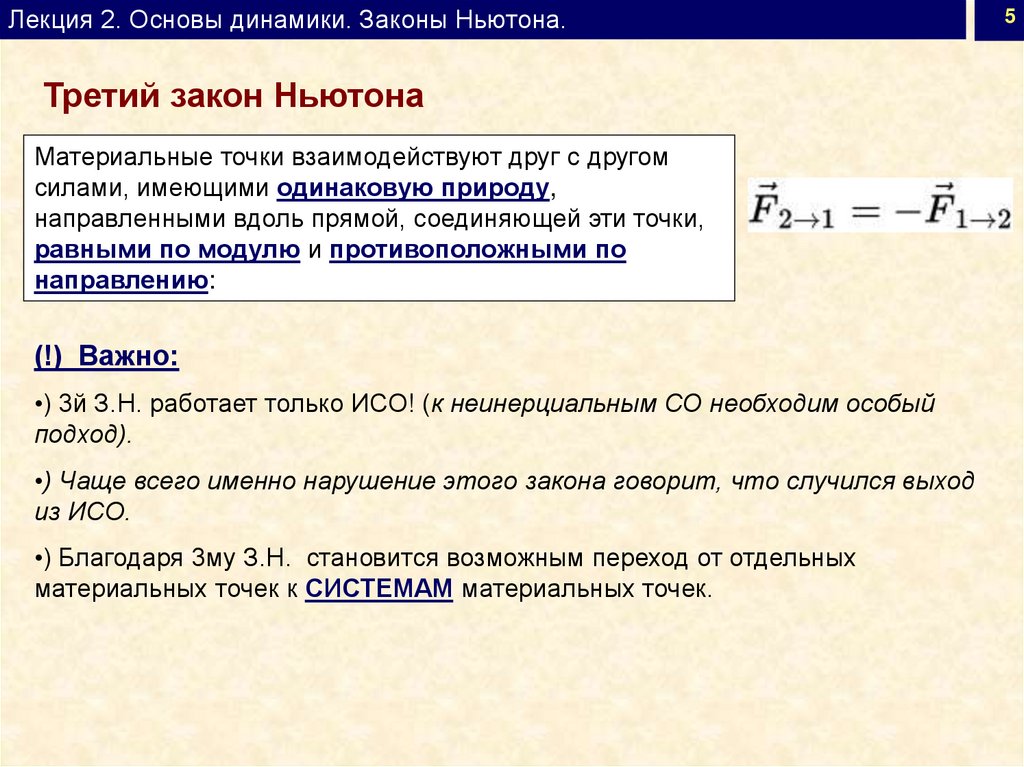
Лекция 2. Основы динамики. Законы Ньютона.
Третий закон Ньютона
Материальные точки взаимодействуют друг с другом
силами, имеющими одинаковую природу,
направленными вдоль прямой, соединяющей эти точки,
равными по модулю и противоположными по
направлению:
(!) Важно:
•) 3й З.Н. работает только ИСО! (к неинерциальным СО необходим особый
подход).
•) Чаще всего именно нарушение этого закона говорит, что случился выход
из ИСО.
•) Благодаря 3му З.Н. становится возможным переход от отдельных
материальных точек к СИСТЕМАМ материальных точек.
5

6.

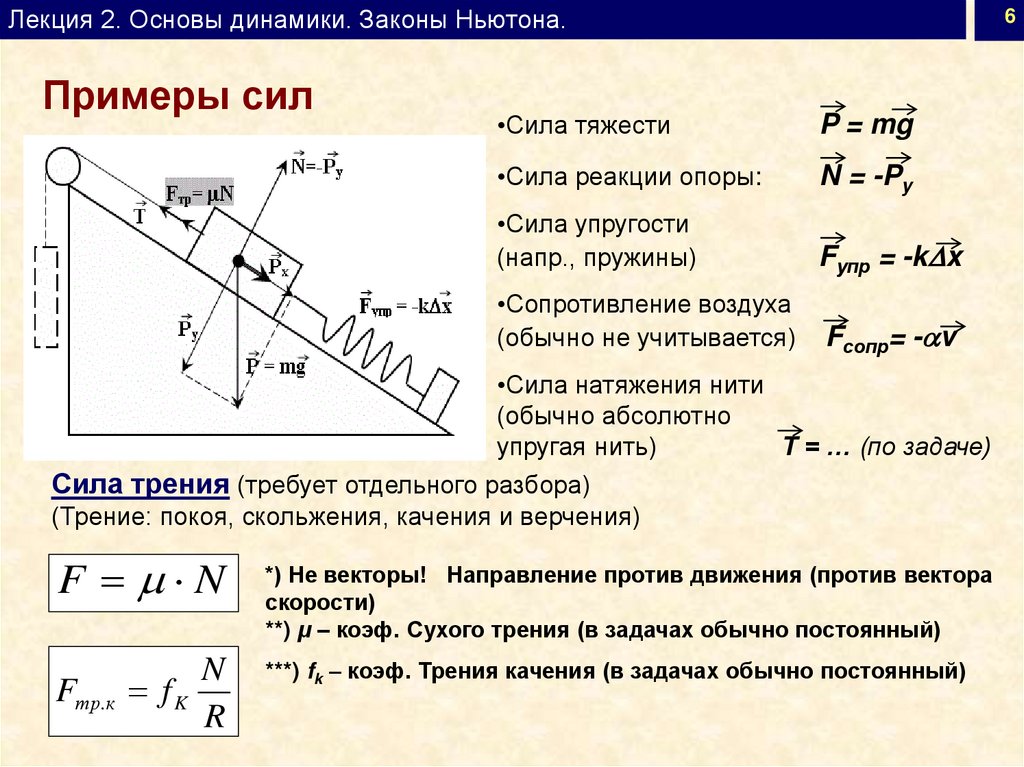
Лекция 2. Основы динамики. Законы Ньютона.
Примеры сил
6
•Сила тяжести
P = mg
•Сила реакции опоры:
N = -Py
•Сила упругости
(напр., пружины)
Fупр = -kDx
•Сопротивление воздуха
(обычно не учитывается)
Fсопр= -av
•Сила натяжения нити
(обычно абсолютно
упругая нить)
T = … (по задаче)
Сила трения (требует отдельного разбора)
(Трение: покоя, скольжения, качения и верчения)
F N
Fтр.к
N
fK
R
*) Не векторы! Направление против движения (против вектора
скорости)
**) μ – коэф. Сухого трения (в задачах обычно постоянный)
***) fk – коэф. Трения качения (в задачах обычно постоянный)

7.

Fi /
Лекция 2. Основы динамики. Законы Ньютона.
7
Закон сохранения импульса
Определения:
•) Механическая система – совокупность М.Т., рассматриваемых как целое
•) Внутренние силы – действующие между М.Т-ми, составляющими систему
•) Внешние силы – действующие на М.Т. силы со стороны внешних тел и полей.
•) Изолированная система – в которой внешние силы равны нулю.
/
Обозначения: Fi
Fi
- равнодействующая внутр.сил на i – МТ
- равнодействующая внешн.сил на i – МТ
Замечаем:
/
F
i 0
n
i 1
Если нет
внешнего
воздействия
dp
0
dt
pсистем ы mi vi const
n
i 1
Согласно
второму З.Н.!
dp n
Fi
dt i 1
•) (!!!) Фундаментальный закон,
выходит за пределы
классической механики !
•) Для изолированной системы

8.

Лекция 2. Основы динамики. Законы Ньютона.
8
Закон движения ЦЕНТРА МАСС
Определения:
•) Центром масс (центром инерции) – геометрическая точка,
характеризующая движение тела или системы тел как целого.
•) Не является тождественным понятию центра тяжести
(хотя чаще всего совпадает).
•) (Забегая вперед) Центром тяжести механической системы называется точка, относительно
которой суммарный момент сил тяжести (действующих на систему) равен нулю.
Для системы М.Т.
m
r
ii
n
rC
i 1
n
m
i 1
mi vi
n
vC
i
i 1
Mc
Для непрерывного распределения масс
Положение Ц.М. системы
1
rC
(r ) r dV
MV
n
pC pi
i 1
M (r )dV
V
Закон движения центра масс
Учитывая, что
pi mi vi
Суммарная масса системы
pс M C vC
n
dvC
MC
Fi
dt
i 1
Центр масс системы движется, как М.Т., в которой сосредоточена вся масса!

9.

Лекция 2. Основы динамики. Законы Ньютона.
Спасибо за внимание!
В следующий раз тема:
Работа и энергия.
Закон сохранения энергии
9