Подготовка модели исследований: система управления с ПИД-регулятором

1. Подготовка модели исследований: система управления с ПИД-регулятором.

2.

1.2. Расчет показателей качества
системы
- Расчет прямых показателей качества
- Расчет косвенных показателей качества
- Расчет интегральных критериев качества

3.

Расчет прямых показателей качества
Для расчета прямых показателей качества необходимо
сформировать схемы в субмоделях, которые включаются в
модель model1
Subsystem1 tpp — расчет критерия качества "время переходного
процесса"
Subsystem2 pregsV — расчет критерия качества
"перерегулирование по скорости"
Subsystem3 pregs — расчет критерия качества
"перерегулирование по управляемой координате".

4.

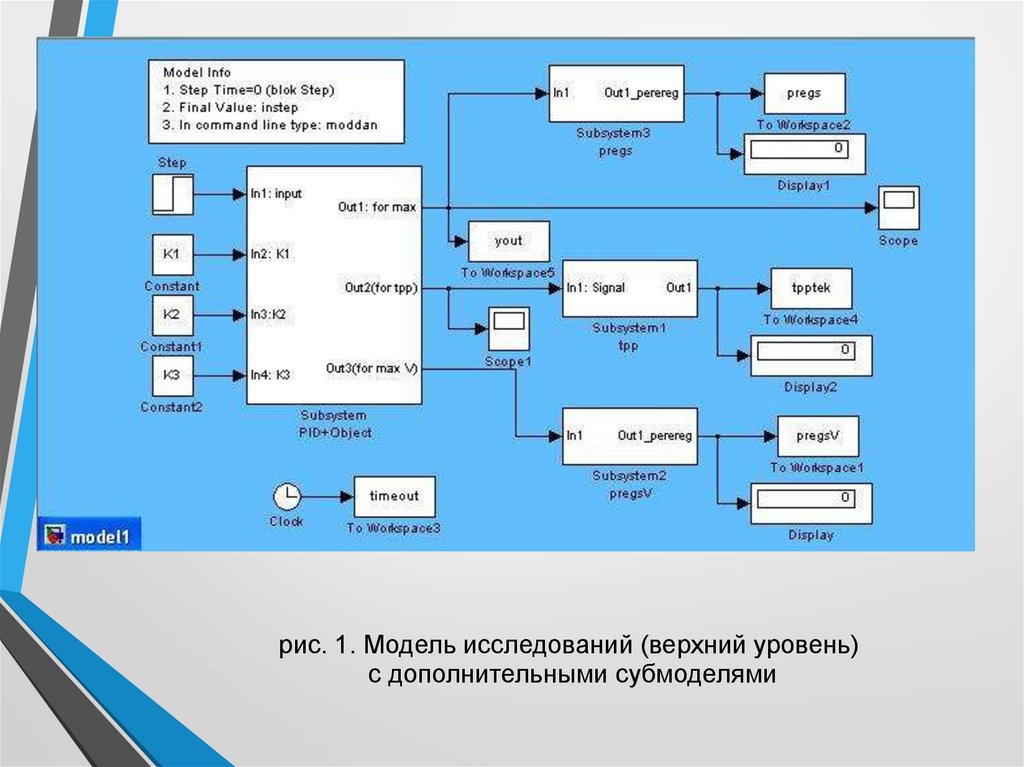
рис. 1. Модель исследований (верхний уровень)
с дополнительными субмоделями

5.

Замечания к модифицированной модели model1.mdl
Новые субмодели предназначены для оценки качества системы, причем
используются прямые критерии качества:
Subsystem1 tpp — расчет критерия качества "время переходного процесса"
Subsystem2 pregsV — расчет критерия качества "перерегулирование по
скорости"
Subsystem3 pregs — расчет критерия качества "перерегулирование по
управляемой координате".
Данные по трем критериям качества динамически выводятся на дисплеи
Display,Display1,Display2.
Для последующей графической интерпретации и численных обработок
значения критериев загружаются в рабочее пространство workspace пакета
MATLAB с помощью блоков ToWorkspace 1-5. Используется представление
выходной информации типа array. Запоминаются следующие
дополнительные массивы чисел в зависимости от времени:
tpptek — время переходного процесса
pregs — перерегулирование по управляемой координате
pregsV — перерегулирование по скорости

6.

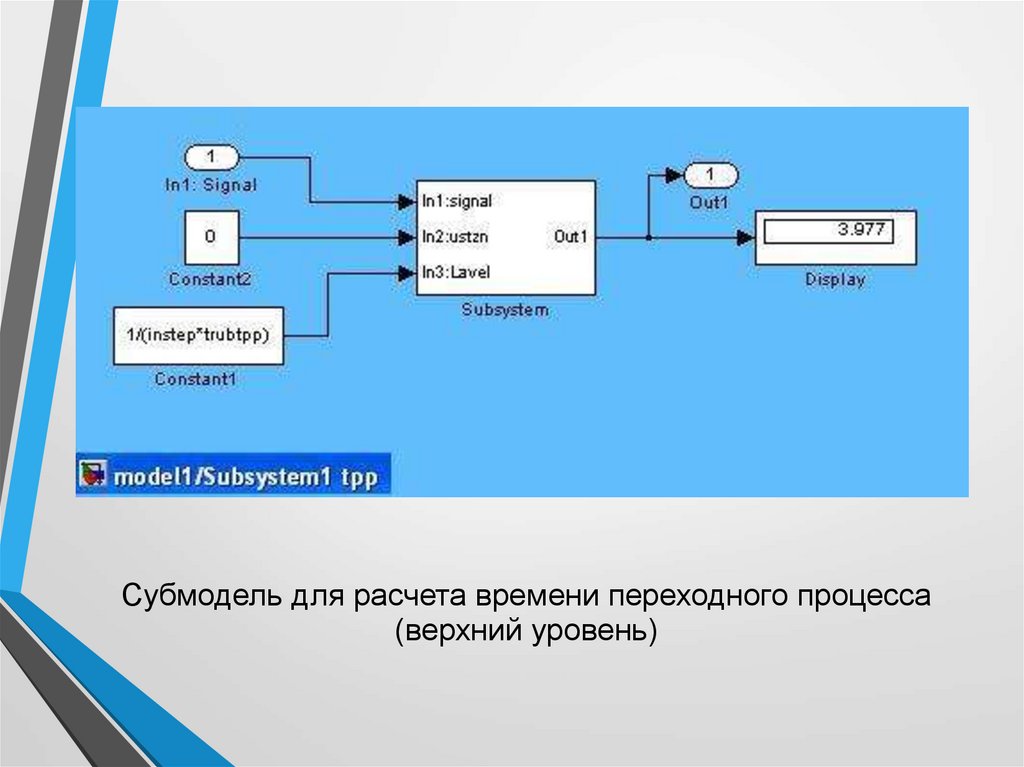
Субмодель для расчета времени переходного процесса
(верхний уровень)

7.

Входными данными служат вход In1: Signal — сигнал
ошибки регулирования и две константы: Constant2=0 —
установившееся значение ошибки и
Constant1=1/(instep*trubtpp) — трубка для оценки
времени переходного процесса величиной trubtpp
(задается обратная величина, масштабированная
величиной входного сигнала instep)
Выход — полученное текущее значение времени
переходного процесса, которое сохраняется в массиве
(см. модель верхнего уровня). Критерий качества
определяется как последнее значение этого массива.
Если эта величина равна времени моделирования,
значит переходной процесс на рассматриваемом
временном интервале еще не завершился. Причина
этого зачастую связана с отсутствием устойчивости
системы при данном наборе параметров.

8.

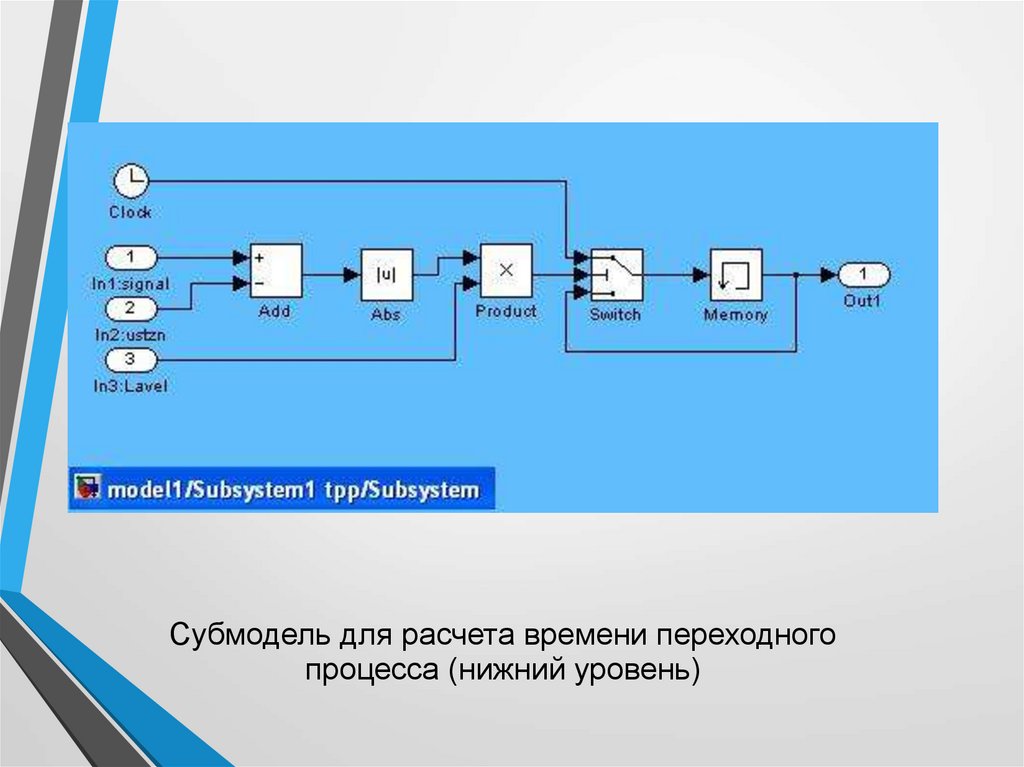
Субмодель для расчета времени переходного
процесса (нижний уровень)

9.

блок Switch: выход блока формируется из первого
или третьего входа, в зависимости от порогового
значения среднего входного сигнала
u2>=Threshold=1
блок memory — задержка на шаг интегрирования
для сохранения предыдущего значения.

10.

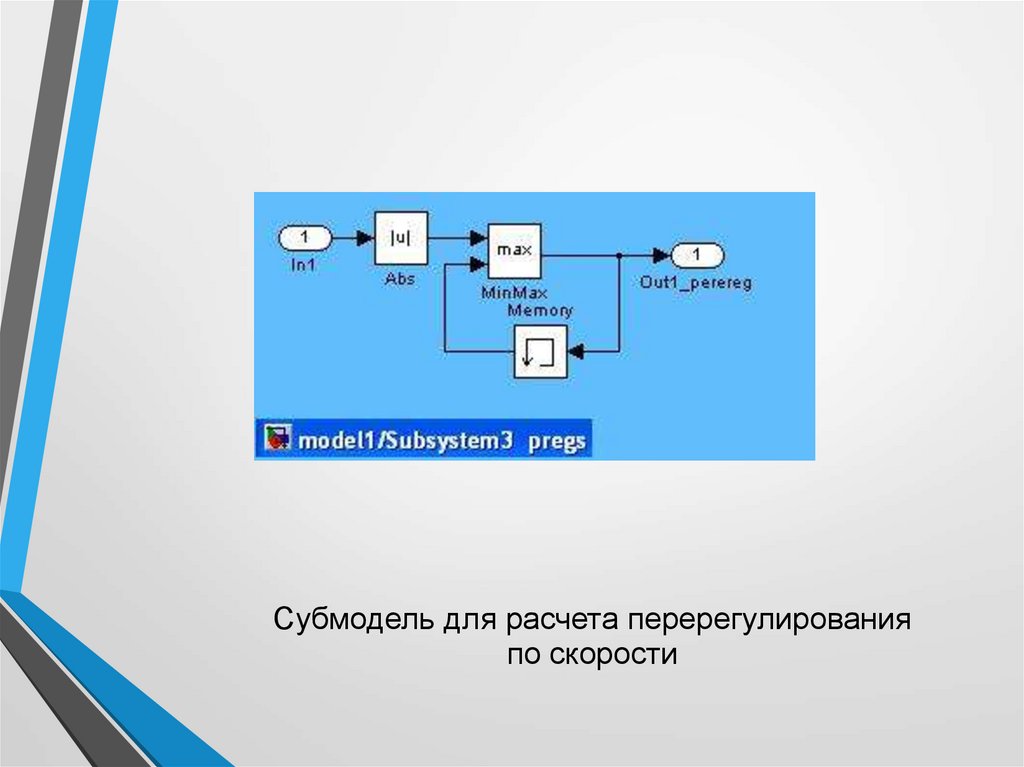
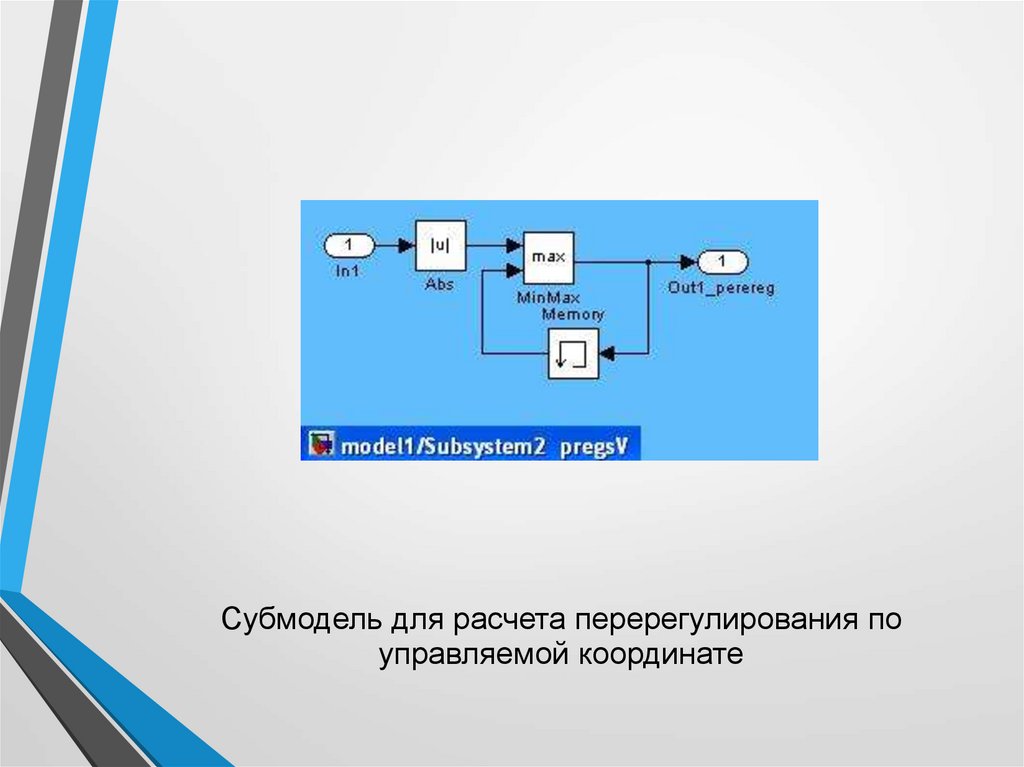
Субмодель для расчета перерегулирования
по скорости

11.

Субмодель для расчета перерегулирования по
управляемой координате

12.

Для извлечения информации о значениях прямых
показателей качества по завершении моделирования
используются команды, применяемые к соответствующим
массивам данных:
krittpp=tpptek(length(tpptek),1)
kritpregs=pregs(length(pregs),1)
kritpregsV=pregsV(length(pregsV),1)
Функция length -определение длины массива

13.

Задание № 2
Определить прямые показатели качества по
итогам моделирования системы model1 с
указанными выше коэффициентами ПИДрегулятора с помощью команд слайда 13

14.

Расчет прямых показателей качества для
линейной или линеаризованной модели,
набранной в пакете Simulink, с помощью
линеаризации моделей(функции пакета Simulink
Control Design)

15.

Функции линейного анализа, относящиеся к Simulink
Control Design, можно использовать как в составе
графического интерфейса пользователя Control and
Estimation Tools Manager (вызывается через цепочку
пунктов меню Simulink->Tools->Control Design >Linear Analysis), так и в виде отдельных команд,
запускаемых в командном окне программы MATLAB
Command Window. Последнее открывает
возможности для автоматизации процесса
линеаризации с помощью m-файла или выполнения
пакетной линеаризации.

16.

Основные шаги линеаризации, которым
соответствуют функции Simulink Control Design:
1. Создание или открытие модели Simulink model
2. Конфигурирование модели
3. Указание оперативных точек
4. Линеаризация модели
5. Анализ результатов и их сохранение.
Графический выбор точек линеаризации вход-выход:
linearization input и output points выполняется
щелчком правой кнопки мыши на линии, куда
необходимо вставить точку и последующим
выбором Linearization Points-Input Point/Output
Point.

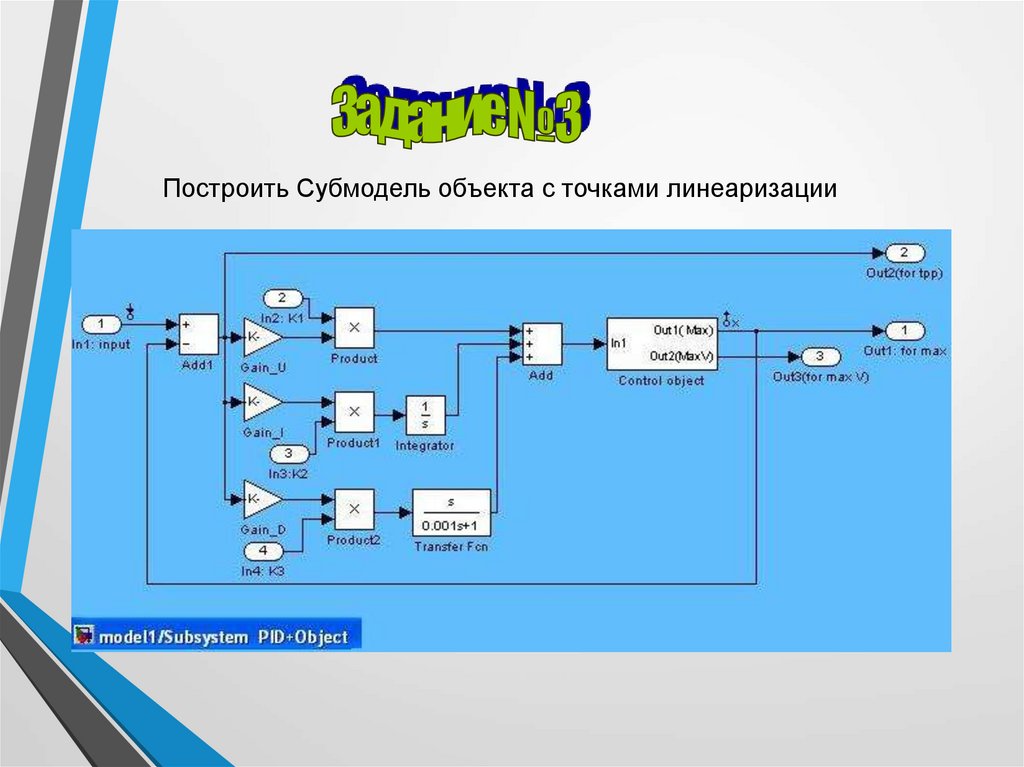
17.

Построить Субмодель объекта с точками линеаризации

18.

Автоматизация расчетов
1. Создание файла-функции расчета
передаточной функции объекта с
текстом
function lintf=mylin(model);
io=getlinio(model);
op=operspec(model);
op=findop(model,op);
lin=linearize(model,op,io);
lintf=tf(lin);
2. Обращение к указанной функции
lintf=mylin('model1')

19.

1. Создать файл-функцию
lintf
2. Рассчитать передаточную функцию замкнутой системы
3. С помощью обозревателя ltiview оценить прямые показатели качества по
переходному процессу:
ltiview('step',lintf) и далее
Время установления (пункт контекстного меню Characteristics ->Settling Time)
Установившееся значение (пункт контекстного меню Characteristics-Steady StateFinal Value))
Положительное перерегулирование, Относительное перерегулирование и Время
максимума.(пункт контекстного меню Characteristics ->Peak Response)
Время нарастания (пункт контекстного меню Characteristics ->Rise Time)
Отчет: Переходной корневому годографу системы процесс в
виде графика и значения прямых показателей качества

20.

Расчет косвенных
показателей качества
Расчет косвенных показателей для модели, набранной в
пакете Simulink, производится с привлечением
линеаризации моделей с помощью функций Simulink Control
Design
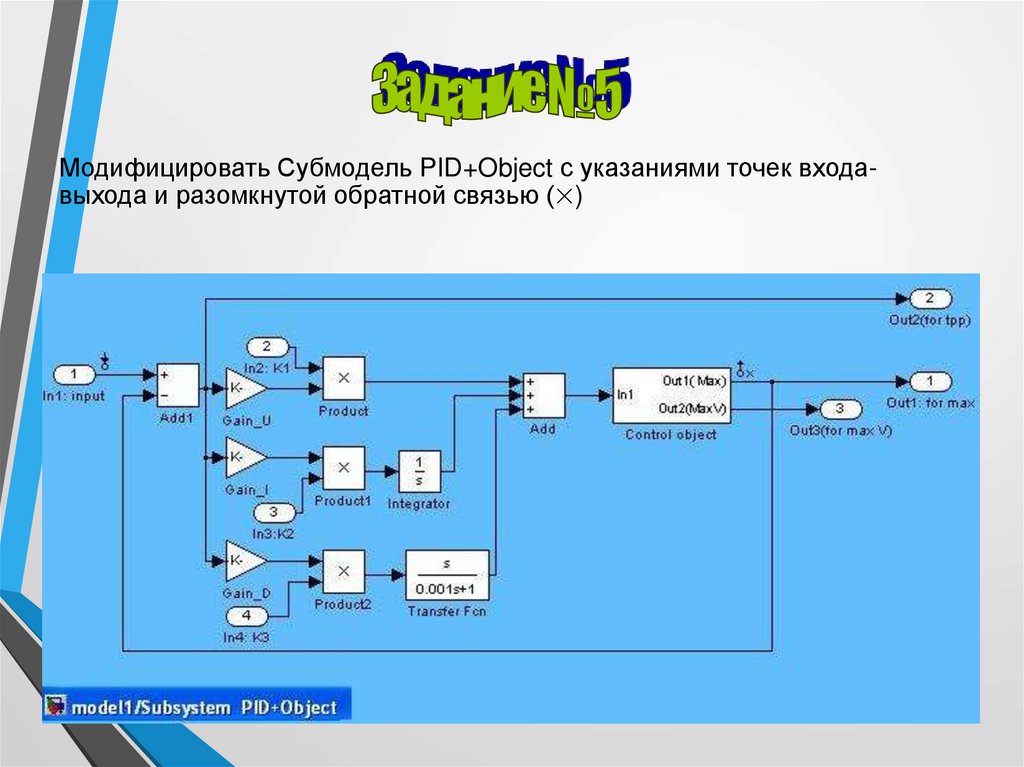
Исследуемая система относится к системам с обратной связью. Для
оценки качества о частотным характеристикам требуется разомкнуть
систему по сигналу главной обратной связи. Для этого нет нужды
реально обрывать главную обратную связь, а достаточно указать на
линии сигнала главной обратной связи свойство Linearization PointsOpen Loop (появится знак ×)

21.

Модифицировать Субмодель PID+Object с указаниями точек входавыхода и разомкнутой обратной связью (×)

22.

1. Рассчитать передаточную функцию разомкнутой системы с
помощью lintf
2. С помощью обозревателя ltiview оценить косвенные
показатели качества по частотной характеристике:
ltiview('bode',lintf)и далее
Запасы устойчивости по амплитуде и фазе
Качественный показатель устойчивости
соответствующей замкнутой системы (Closed Loop
Stable? )
Отчет: Передаточная функция, график частотной
характеристики и значения косвенных показателей
качества

23.

Исследования нулей и полюсов
Корни системы рассчитываются по команде
eig(lintf)
Полная информация о модели(нули zc, полюса pc, коэффициент усиления
k) получается при использовании команд
[zc,pc,k]=zpkdata(lintf)
z=cell2mat(z)
p=cell2mat(p)
Графическое представление карты нулей и полюсов выполняется по
команде
pzmap(lintf)
Перемещение корней при изменении коэффициента усиления системы по
команде
rlocus(lintf)
соответствует корневому годографу системы

24.

1. Восстановить замкнутую систему (убрать флажок Open Loop и
вновь рассчитать передаточную функцию линеаризованной
системы
2. Рассчитать корни системы
3. Рассчитать нули zc, полюса pc, коэффициент усиления k
4. Получить графическое представление карты нулей и полюсов
5. Построить корневой годограф системы
Отчет: Значения вышеперечисленных косвенных
показателей качества, карта нулей-полюсов, годограф

25.

Расчет интегральных
показателей качества
Интегральные оценки качества систем — оценки, полученные
путем интегрирования прямых показателей качества на
времени наблюдения T. Обычно верхний предел
интегрирования T выбирается так, чтобы интеграл стремился к
конечному значению. В качестве верхнего предела T можно
брать время переходного процесса в системе.

26.

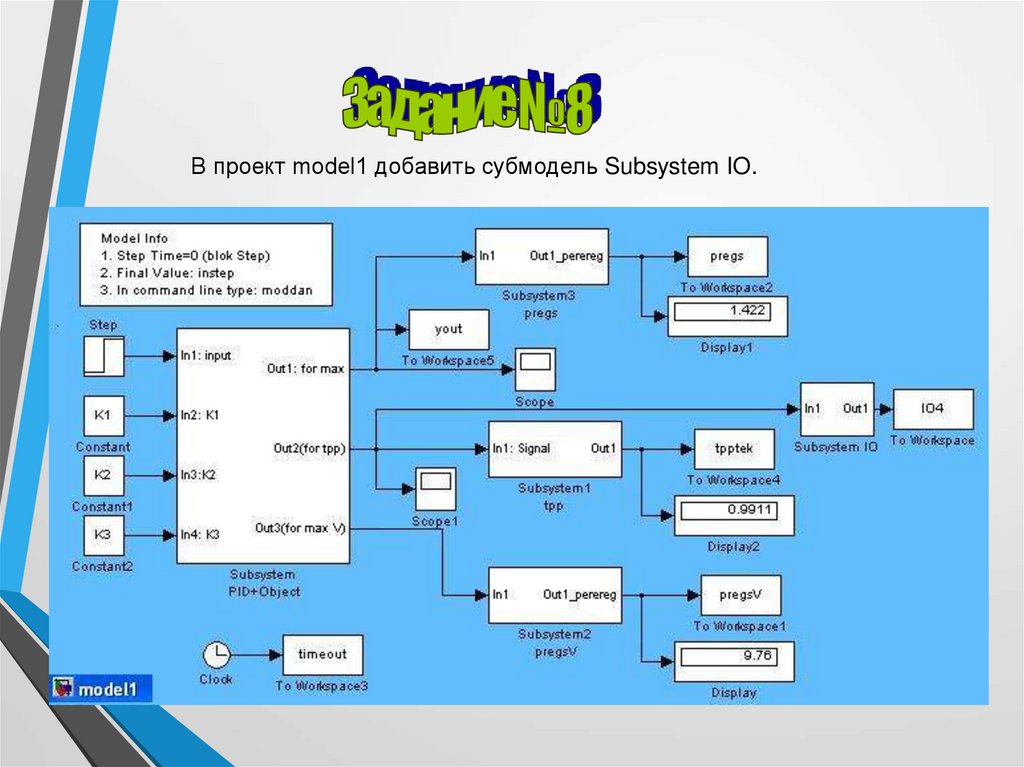
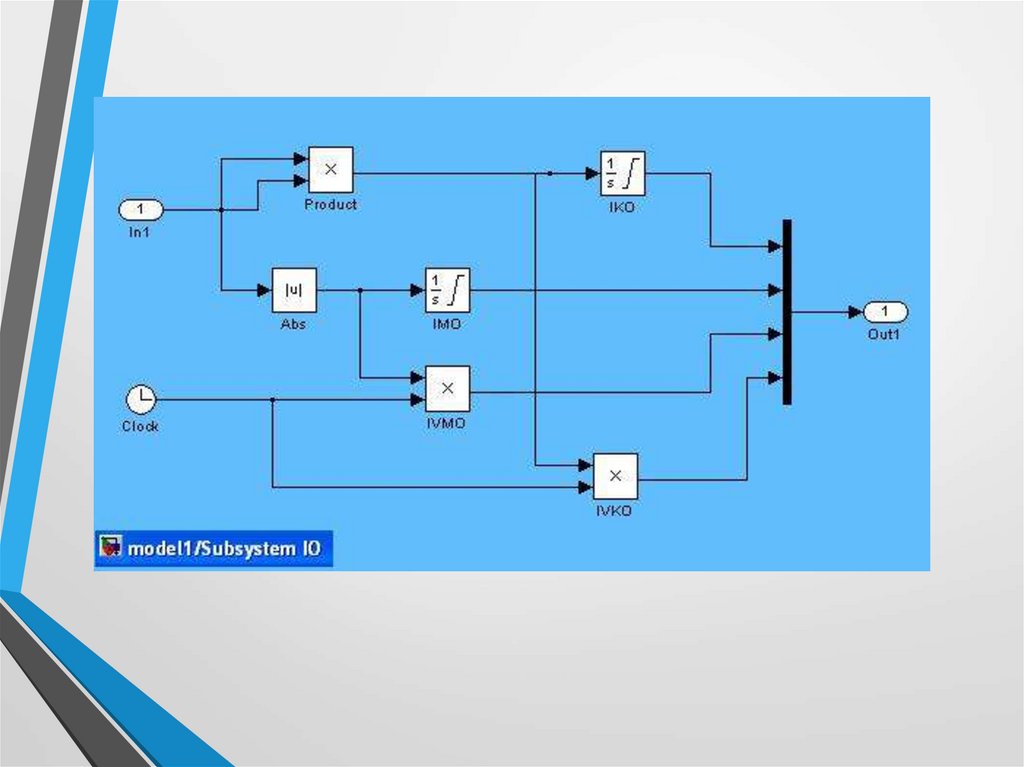
В проект model1 добавить субмодель Subsystem IO.

27.

28.

Рассчитываются четыре интегральные оценки качества. В любом случае входом
является значение ошибки (входной порт In1). Для взвешенных оценок
дополнительно используется таймер Clock. Интегрирование ведется в пределах
от 0 до tmod (определяется в файле исходных данных moddan). Практика
показывает, что для данной модели в устойчивом состоянии достаточно взять
tmod=7).
Рассчитанные оценки собираются в вектор с помощью мультиплексора и
передаются в рабочее пространство MATLAB (уже в верхней модели) в виде
матрицы IO4. Порядок интегралов следующий:
Интеграл от квадрата ошибки (ИКО)
Интеграл от модуля ошибки (ИМО)
Интеграл от взвешенного модуля ошибки ИВМО
Интеграл от взвешенного квадрата ошибки ИВКО
Для извлечения информации по итогам интегрирования используются команды
IKO=IO4(length(IO4),1)
IMO=IO4(length(IO4),2)
IVMO=IO4(length(IO4),3)
IVKO=IO4(length(IO4),4)
где length — функция для определения размерности массива.

29.

Рассчитать интегральные критерии качества при базовых
коэффициентах ПИД-регулятора
Отчет: Значения вышеперечисленных косвенных
показателей качества

30.

Для оценки квадратичного критерия качества требуется перевести
линеаризованную систему lintf в ss-представление, т.е. описание
системы в пространстве состояний.
ssmodel1=ss(lintf)
Если управляющее воздействие u=[1]. моделирование системы
осуществляется по командам
t=0:0.01:10;
u=1*ones(size(t));
[y,x]=LSIM(ssmodel1,u,t)
plot(t,y)
Следующий код (файл kvkk.m) позволяет рассчитать
квадратичный критерий качества JK, для интегрирования
используется функция MATLAB trapz

31.

ssmodel1=ss(lintf);
[A,B,C,D] = ssdata(ssmodel1)
[n,n]=size(A)
[n,r]=size(B)
[l,n]=size(C)
t=0:0.01:10;
u=1*ones(size(t));
u=u'
[y,T,x]=LSIM(ssmodel1,u,t)
plot(t,y)
nt=length(t)
FI=diag(ones(n,1))
FIK=diag(ones(n,1))
PSI=diag(ones(r,1))
for i=1:nt
kkx(i,1)=x(i,:)*FI*x(i,:)';
end
for i=1:nt
kku(i,1)=u(i,:)*PSI*u(i,:)';
end
xk=x(length(x),:);
kkxk=xk*FIK*xk'
trapz(kkx)
trapz(kku)
Jk=trapz(kkx)+trapz(kku)+kkxk

32.

1. Перевести линеаризованную систему lintf в ss-представление
2. Промоделировать систему при управляющем воздействии u=[1]
3. Создать файл kvkk.m
4. Рассчитать значения:
- составляющая квадратичного критерия, связанная с отклонениями фазовых
координат в конечный момент времени kkxk
-составляющая квадратичного критерия, связанная с отклонениями фазовых
координат kkx
-- составляющая квадратичного критерия, связанная с дополнительными
управляющими воздействиями kku
-- общее значение квадратичного критерия качества
Отчет: Значения вышеперечисленных косвенных
показателей качества, график переходного процесса в
системе