Тригонометрия

1. Тригонометрия

Автор:
МбОУ СОШ №4
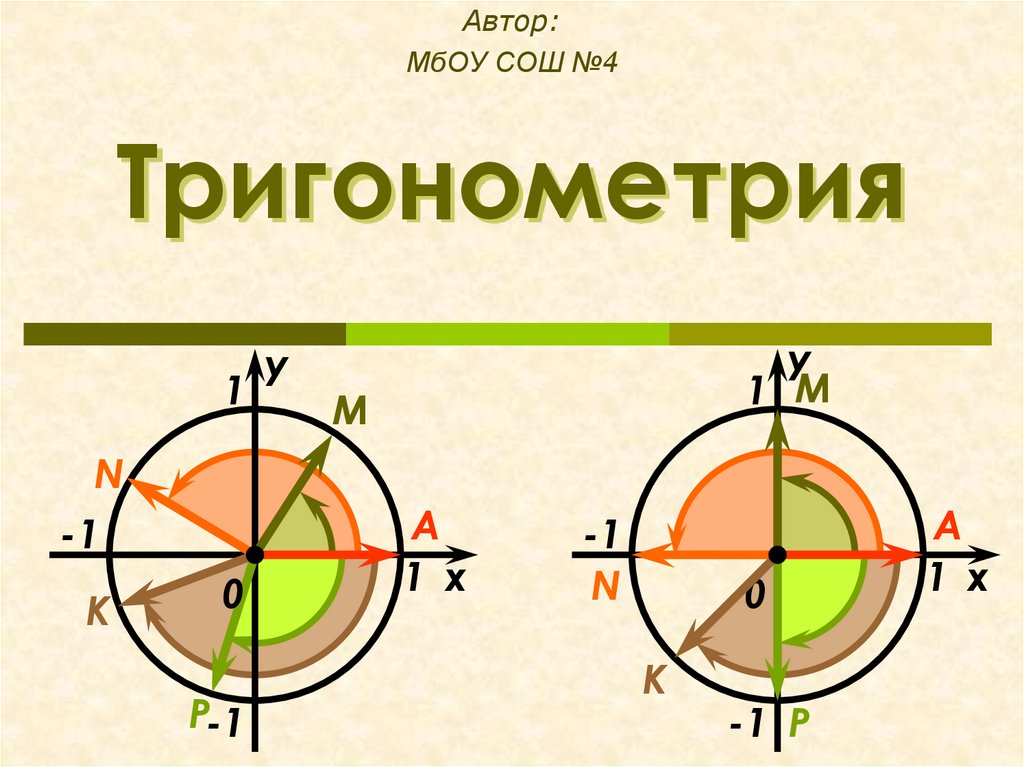
Тригонометрия
1
у
у
1 М
М
N
-1
K
0
P-1
А
1 x
-1
N
0
K
-1 P
А
1 x

2. Содержание

Простейшие тригонометрические уравнения
Простейшие тригонометрические неравенства

3. Простейшие тригонометрические уравнения

Определение арксинуса.
Уравнение sin t = a.
Определение арккосинуса.
Уравнение cos t = a.
Определение арктангенса.
Уравнение tg t = a.
Определение арккотангенса.
Уравнение ctg t = a.

4. Определение арксинуса

Арксинусом числа а называется
такой угол из промежутка [− 0,5π; 0,5π],
синус которого равен а, где lаl ≤ 1.
arcsin a = t , sin t = a
где t [− 0,5π; 0,5π]
а [− 1; 1]
sin(arcsin a) = a, а [− 1; 1]
arcsin(sin t) = t, t [− 0,5π; 0,5π]

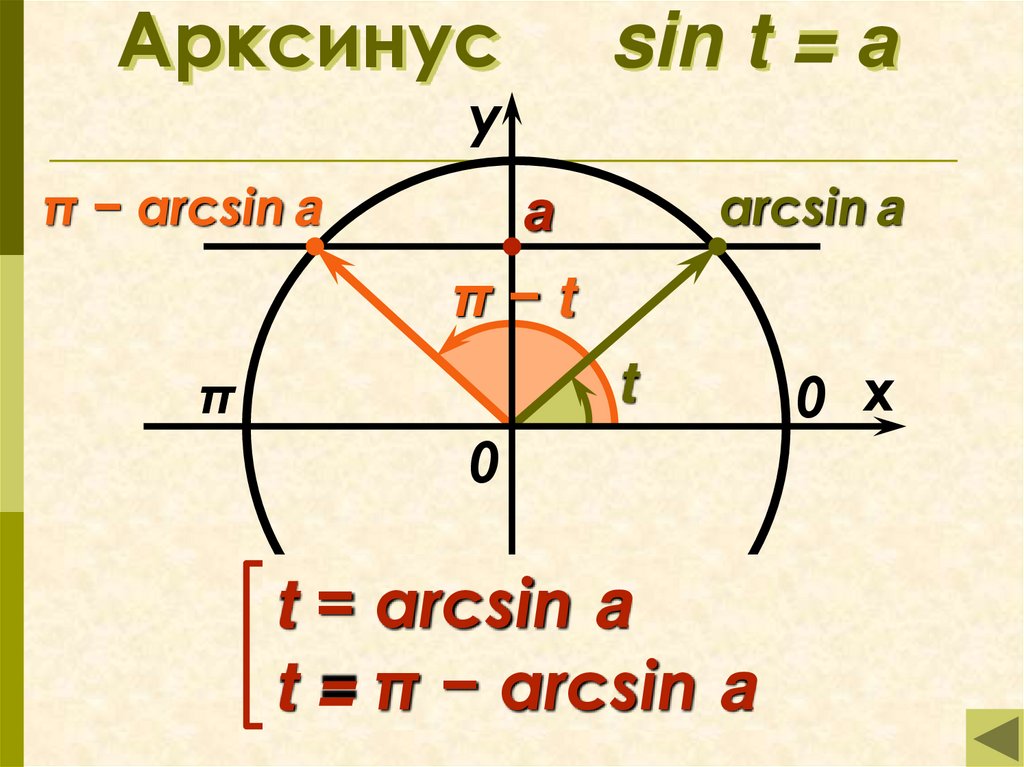
5. Арксинус sin t = а

у
π − arcsin a
arcsin a
а
π−t
t
π
0
t = arcsin a
t = π − arcsin a
0 x

6. Определение арккосинуса

Арккосинусом числа а называется
такой угол из промежутка [ 0; π],
косинус которого равен а, где lаl ≤ 1.
arccos a = t , cos t = a
где t [ 0; π]
а [− 1; 1]
cos(arccos a) = a, a [-1; 1]
arccos(cos t) = t, t [ 0; π]

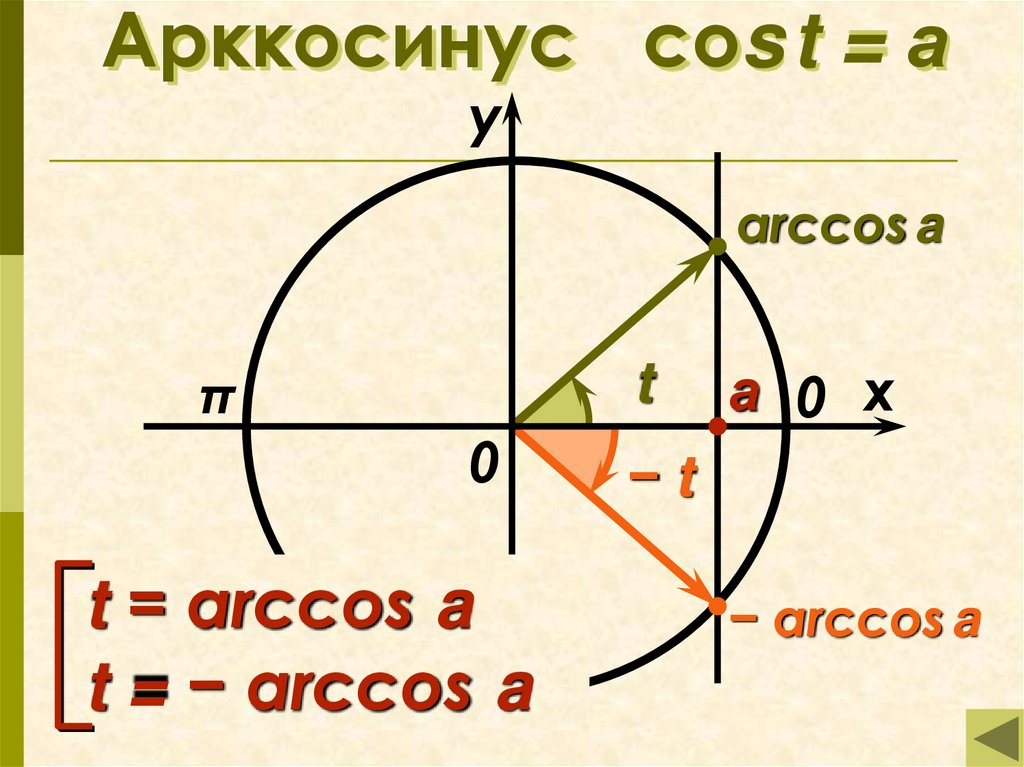
7. Арккосинус cos t = а

у
arccos a
t
π
0
t = arccos a
t = − arccos a
а 0 x
−t
− arccos a

8. Определение арктангенса

Арктангенсом числа а называется
такой угол из промежутка (− 0,5π; 0,5π),
тангенс которого равен а.
arctg a = t , tg t = a
где t (− 0,5π; 0,5π)
tg(arctg a) = a
arctg (−a) = − arctg a
arctg(tg t) = t, t (− 0,5π; 0,5π)

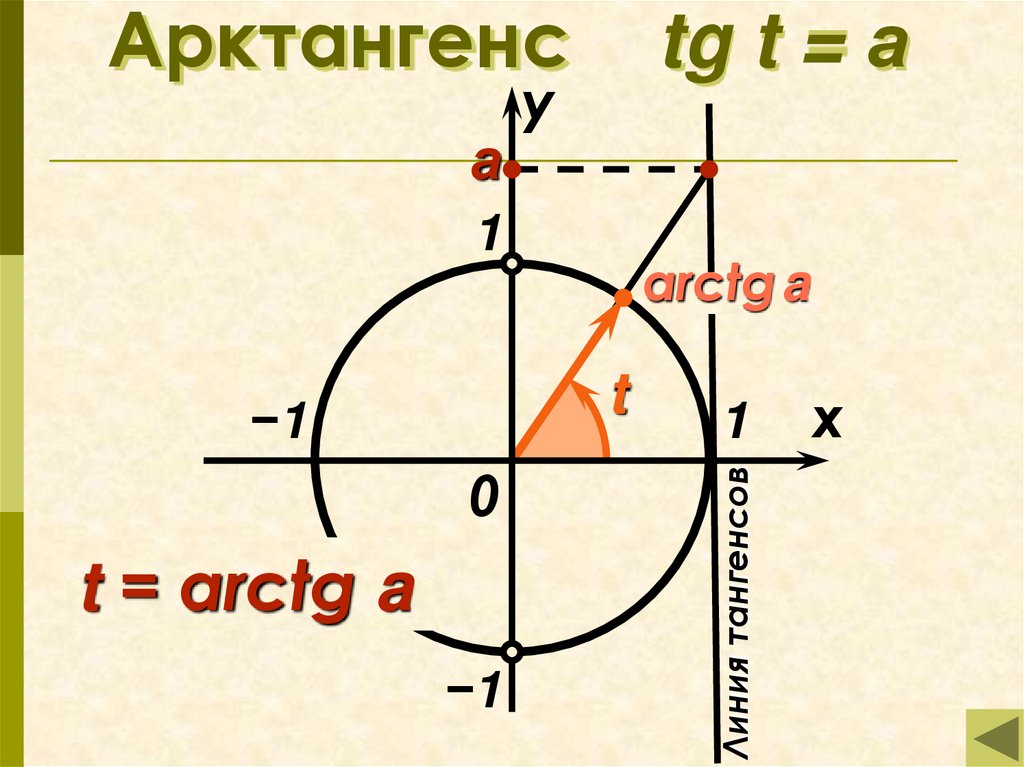
9. Арктангенс tg t = а

Арктангенс
у
1
arctg a
t
−1
0
t = arctg a
−1
1
Линия тангенсов
а
tg t = а
x

10. Определение арккотангенса

Арккотангенсом числа а называется
такой угол из промежутка (0; π),
котангенс которого равен а.
arcсtg a = t , сtg t = a
где t (0; π)
сtg(arсctg a) = a
arсctg (−a) = π − arcсtg a
arcсtg(сtg t) = t, t (0; π)

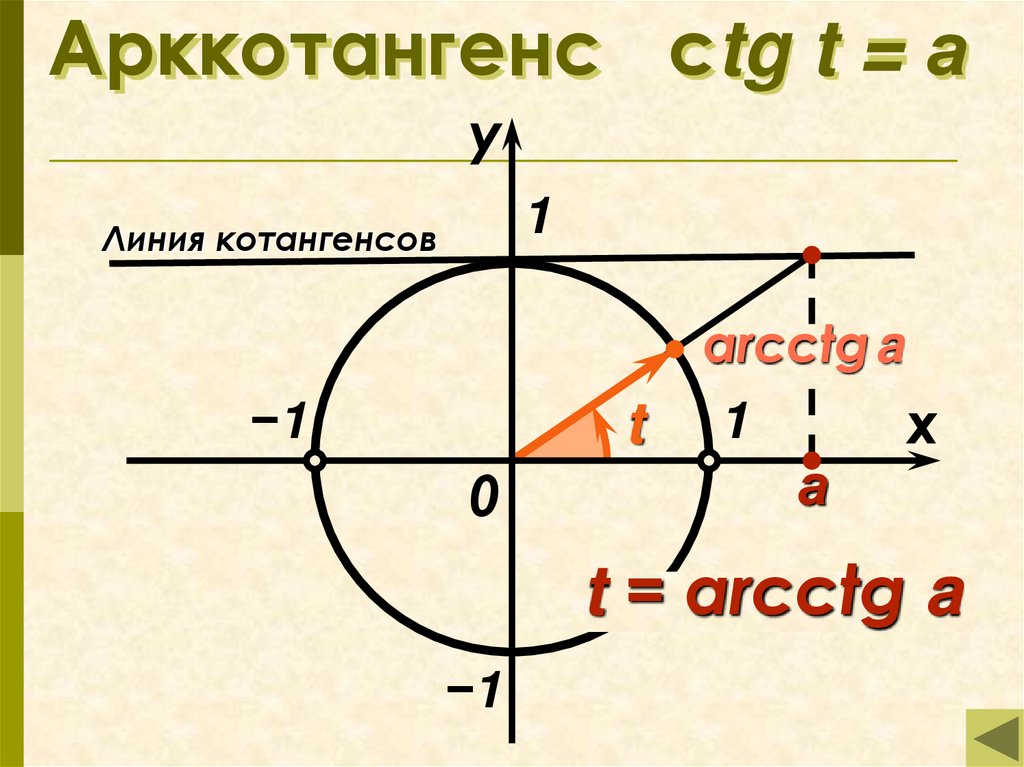
11. Арккотангенс сtg t = а

у
1
Линия котангенсов
−1
t
0
arcctg a
1
x
а
t = arcсtg a
−1

12. Простейшие тригонометрические неравенства

Решение тригонометрического неравенства sin t < a.
Решение тригонометрического неравенства sin t > a.
Решение тригонометрического неравенства cos t < a.
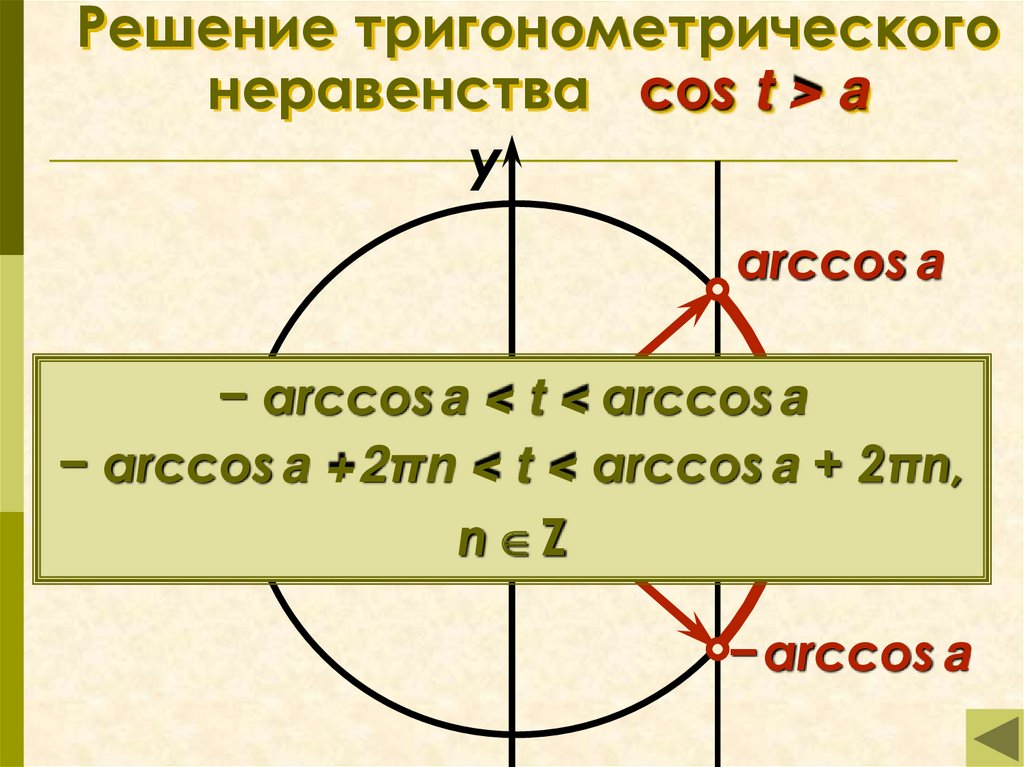
Решение тригонометрического неравенства cos t > a.
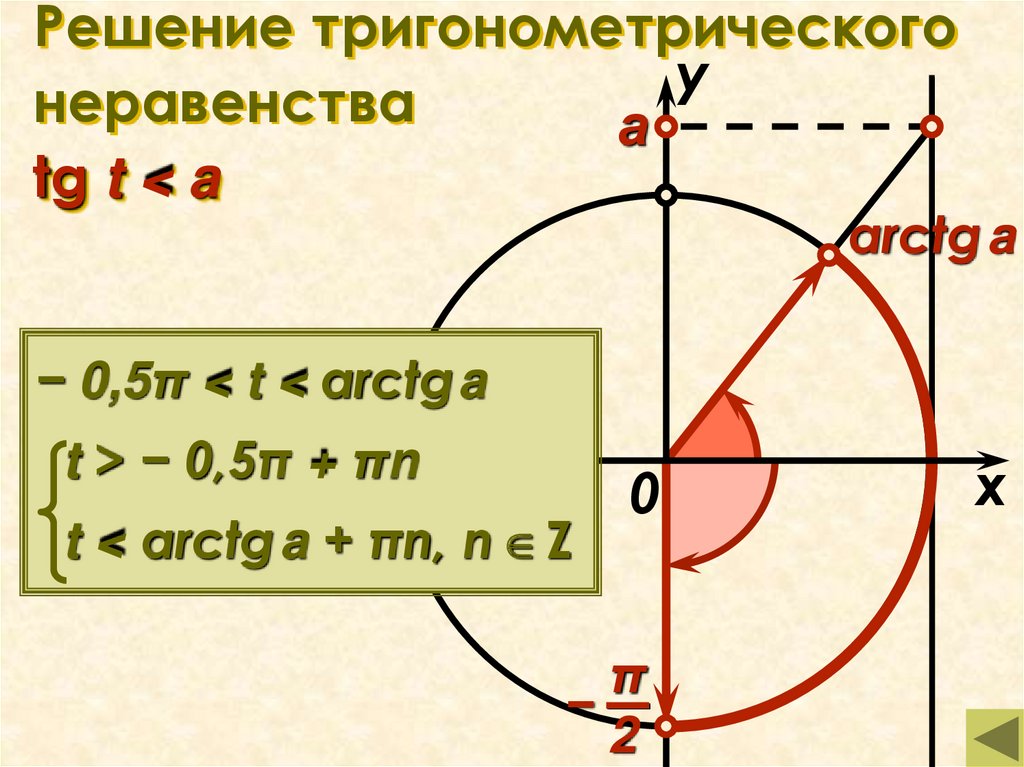
Решение тригонометрического неравенства tg t < a.
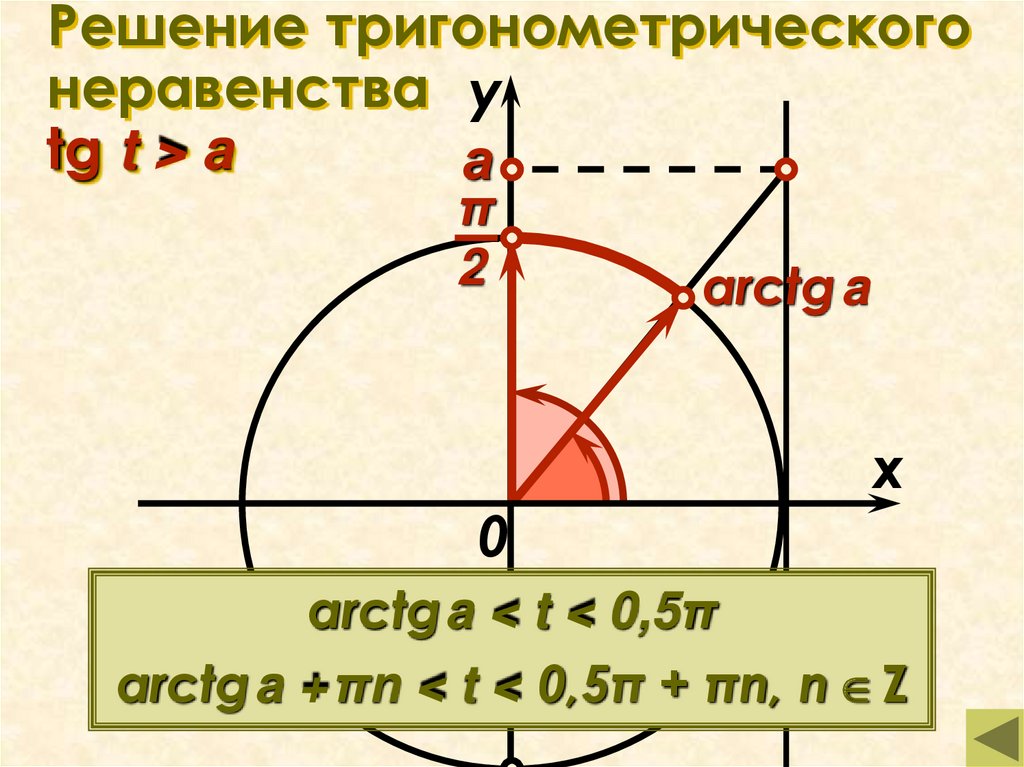
Решение тригонометрического неравенства tg t > a.
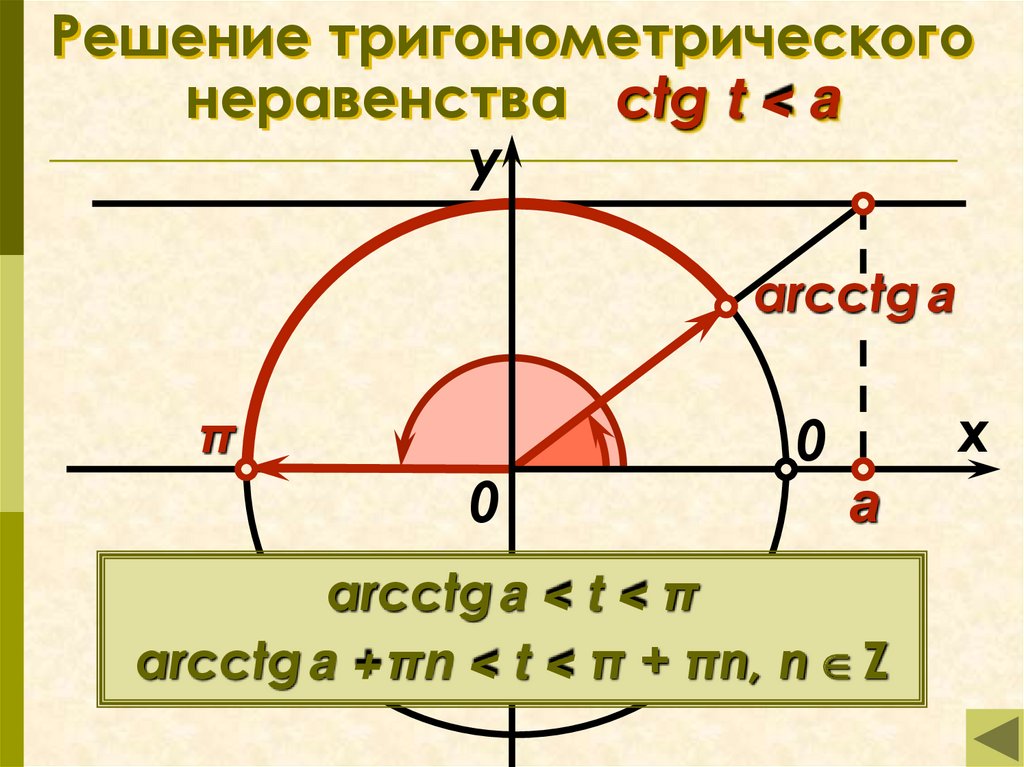
Решение тригонометрического неравенства ctg t < a.
Решение тригонометрического неравенства ctg t > a.

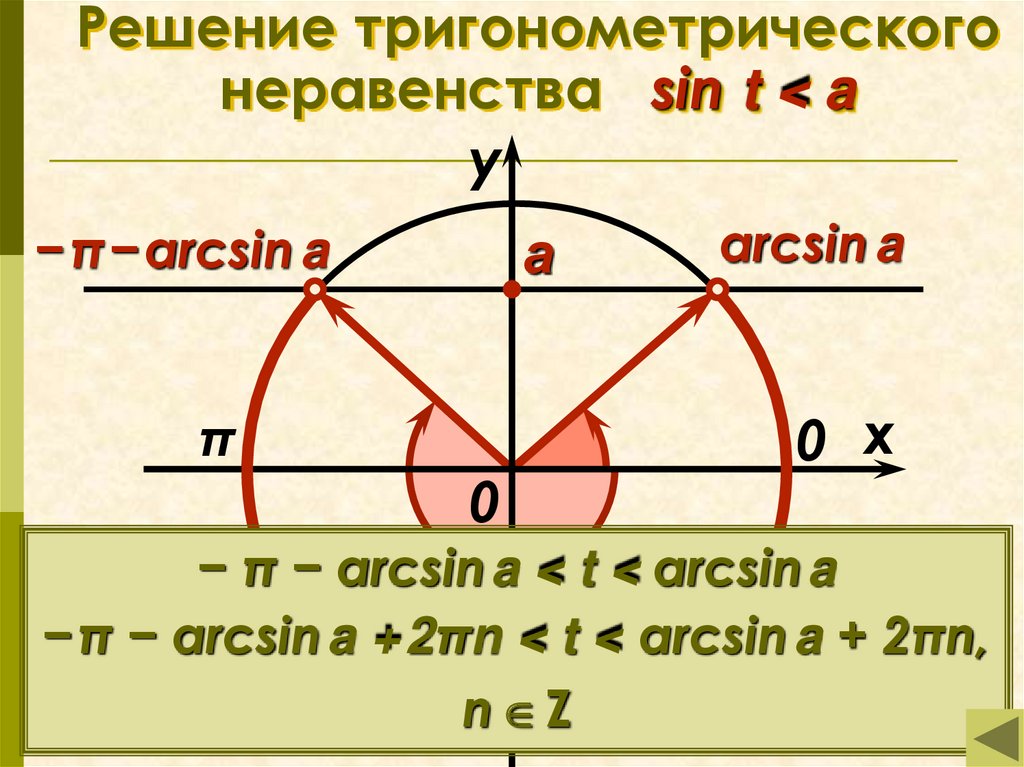
13. Решение тригонометрического неравенства sin t < a

Решение тригонометрического
неравенства sin t < a
у
−π−arcsin a
π
а
0
arcsin a
0 x
− π − arcsina < t < arcsina
−π − arcsin a +2πn < t < arcsin a + 2πn,
n Z

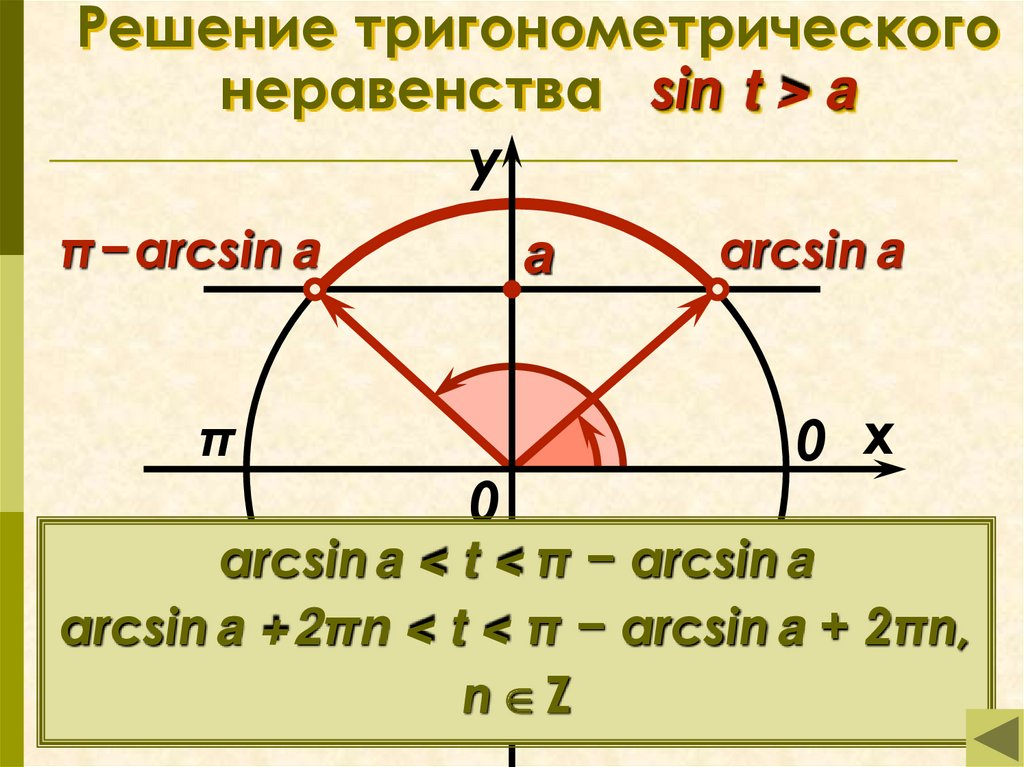
14. Решение тригонометрического неравенства sin t > a

Решение тригонометрического
неравенства sin t > a
у
π−arcsin a
π
а
0
arcsin a
0 x
arcsina < t < π − arcsina
arcsin a +2πn < t < π − arcsin a + 2πn,
n Z

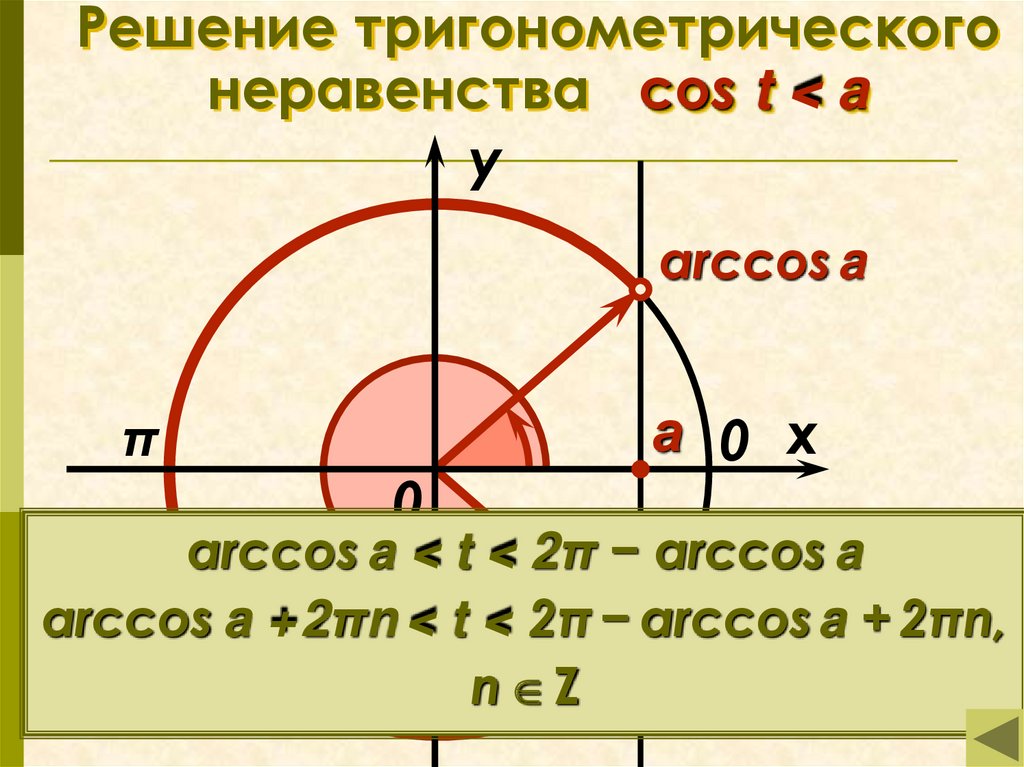
15. Решение тригонометрического неравенства cos t < a

Решение тригонометрического
неравенства cos t < a
у
arccos a
π
0
а 0 x
arccos a < t < 2π − arccos a
arccos a +2πn < t < 2π − arccos a + 2πn,
2π − arccos a
n Z

16. Решение тригонометрического неравенства cos t > a

Решение тригонометрического
неравенства cos t > a
у
arccos a
− arccosa < t < arccosa
а 0 x
π
− arccos a +2πn < t < arccos a + 2πn,
0
n Z
−arccos a

17. Решение тригонометрического неравенства tg t < a

Решение тригонометрического
у
неравенства
а
tg t < a
arctg a
− 0,5π < t < arctga
t > − 0,5π + πn
t < arctg a + πn, n Z
0
π
−
2
x

18. Решение тригонометрического неравенства tg t > a

Решение тригонометрического
неравенства у
tg t > a
а
π
2
0
arctg a
x
arctga < t < 0,5π
arctg a +πn < t < 0,5π + πn, n Z

19. Решение тригонометрического неравенства ctg t < a

Решение тригонометрического
неравенства ctg t < a
у
arcctg a
π
0
0
x
а
arcctga < t < π
arcctg a +πn < t < π + πn, n Z

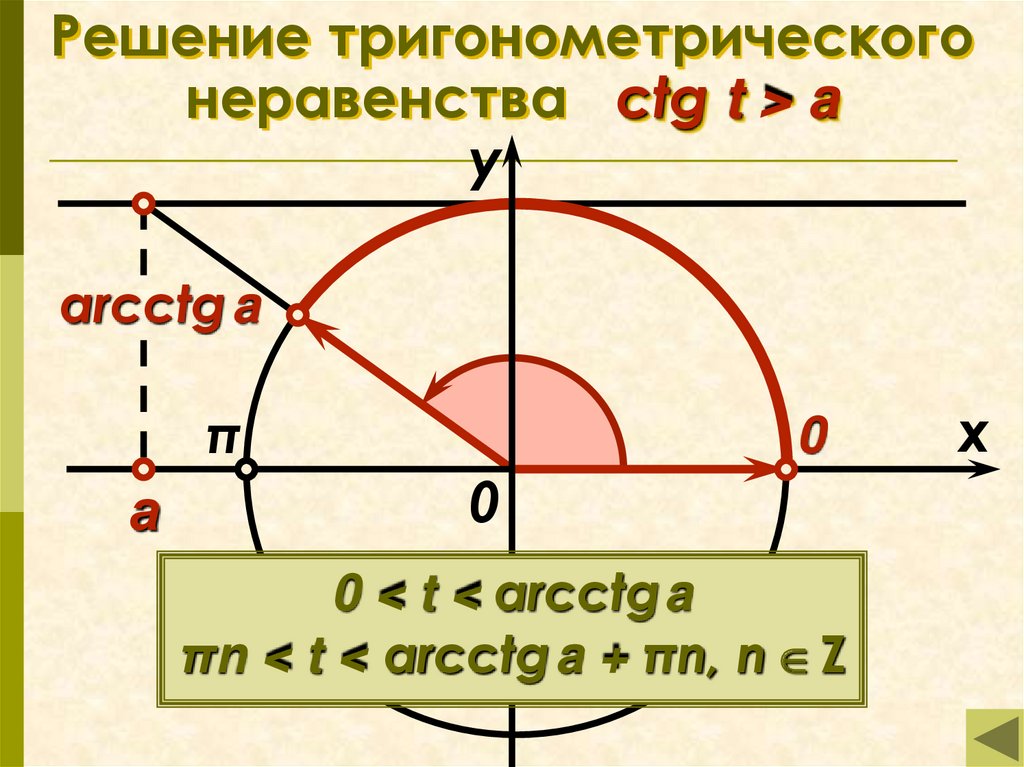
20. Решение тригонометрического неравенства ctg t > a

Решение тригонометрического
неравенства ctg t > a
у
arcctg a
π
а
0
0
0 < t < arcctga
πn < t < arcctg a + πn, n Z
x