Similar presentations:
Градусы и радианы
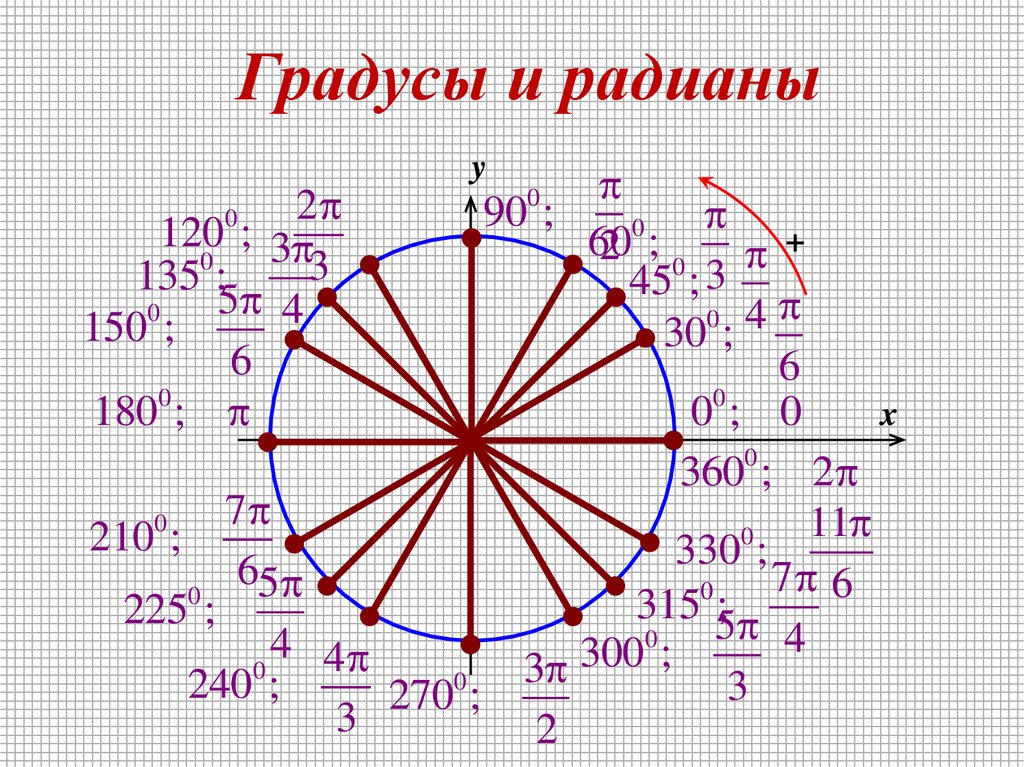
1. Градусы и радианы
y90 ;
0
60
2 ;0 +
45 ; 3
0 4
30 ;
6
x
00 ; 0
0
0
360 ; 2
7
0
11
0
210 ;
330
;
6
7 6
5
0
0
315 5;
225 ;
0
4
4
300
;
4
3
0
2400 ;
3
270 ;
3
2
2
0
120 ; 3
3
1350 ;
5 4
0
150 ;
6
1800 ;
0
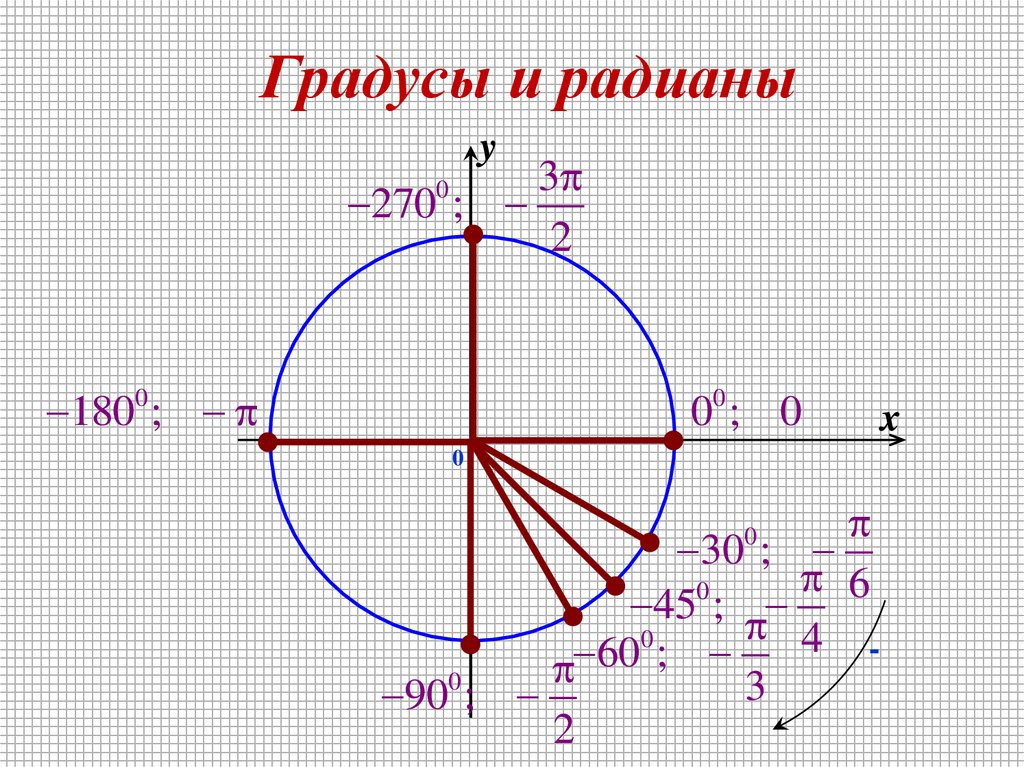
2. Градусы и радианы
y3
270 ;
2
0
1800 ;
00 ; 0
x
0
30 ;
6
0
45 ;
0
4
60
;
0
3
90 ;
2
0
-
3.
4.
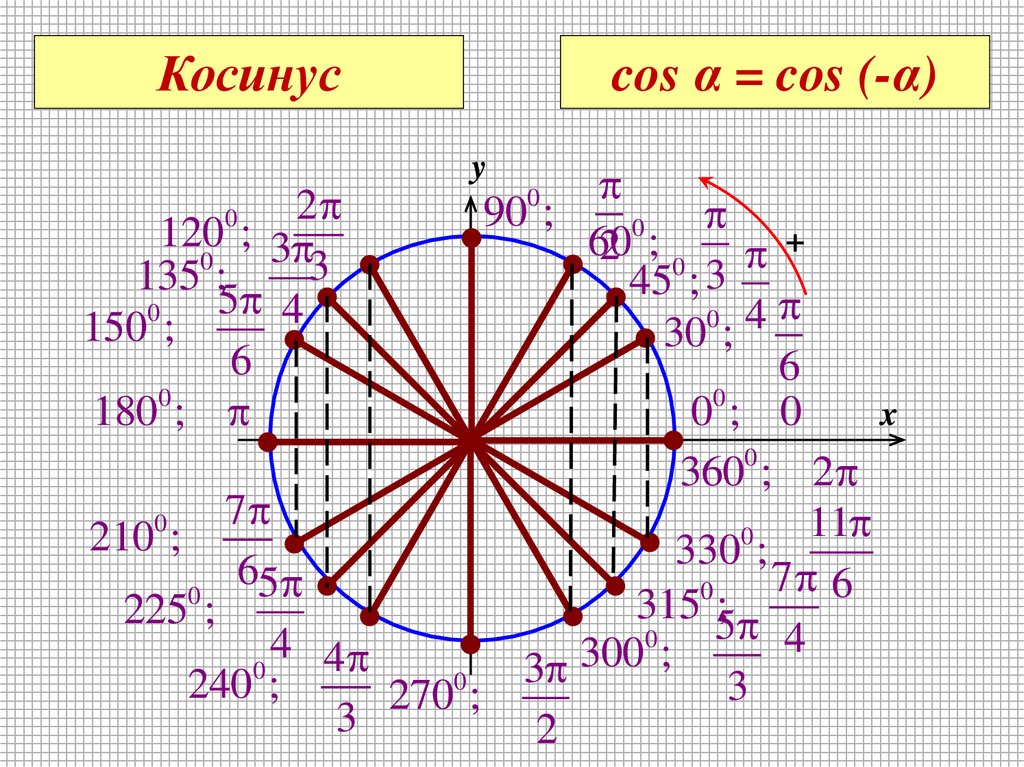
Косинусcos α = cos (-α)
y
90 ;
0
60
2 ;0 +
45 ; 3
0 4
30 ;
6
x
00 ; 0
0
0
360 ; 2
7
0
11
0
210 ;
330
;
6
7 6
5
0
0
315 5;
225 ;
0
4
4
300
;
4
3
0
2400 ;
3
270 ;
3
2
2
0
120 ; 3
3
1350 ;
5 4
0
150 ;
6
1800 ;
0
5.
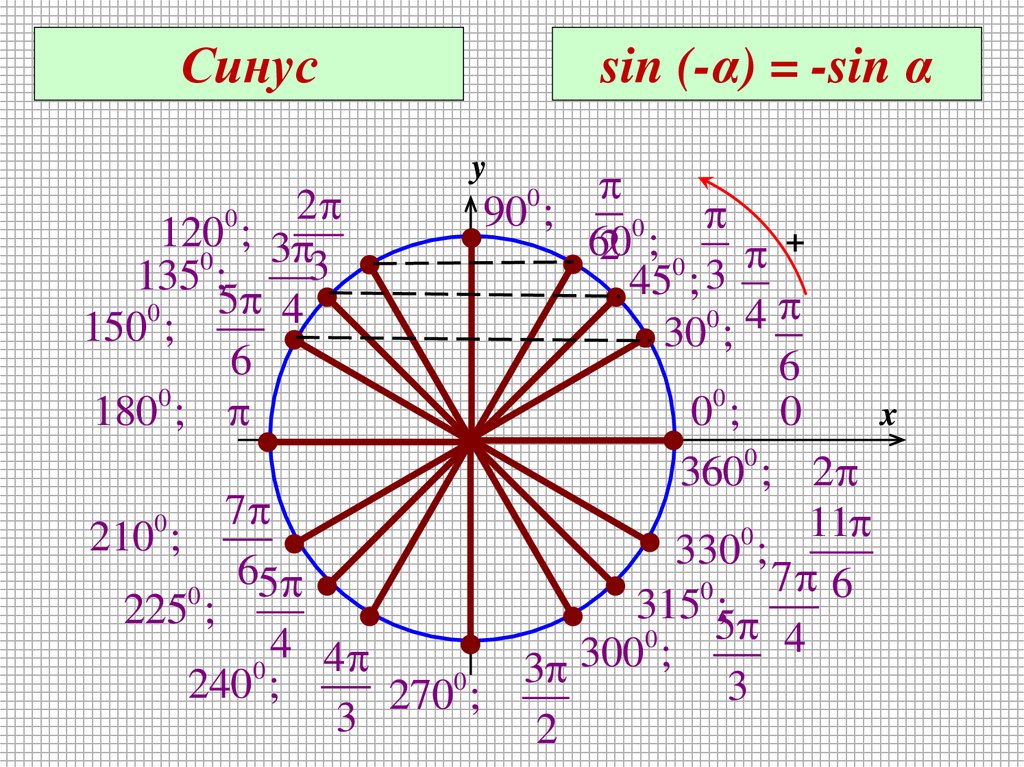
Синусsin (-α) = -sin α
y
90 ;
0
60
2 ;0 +
45 ; 3
0 4
30 ;
6
x
00 ; 0
0
0
360 ; 2
7
0
11
0
210 ;
330
;
6
7 6
5
0
0
315 5;
225 ;
0
4
4
300
;
4
3
0
2400 ;
3
270 ;
3
2
2
0
120 ; 3
3
1350 ;
5 4
0
150 ;
6
1800 ;
0
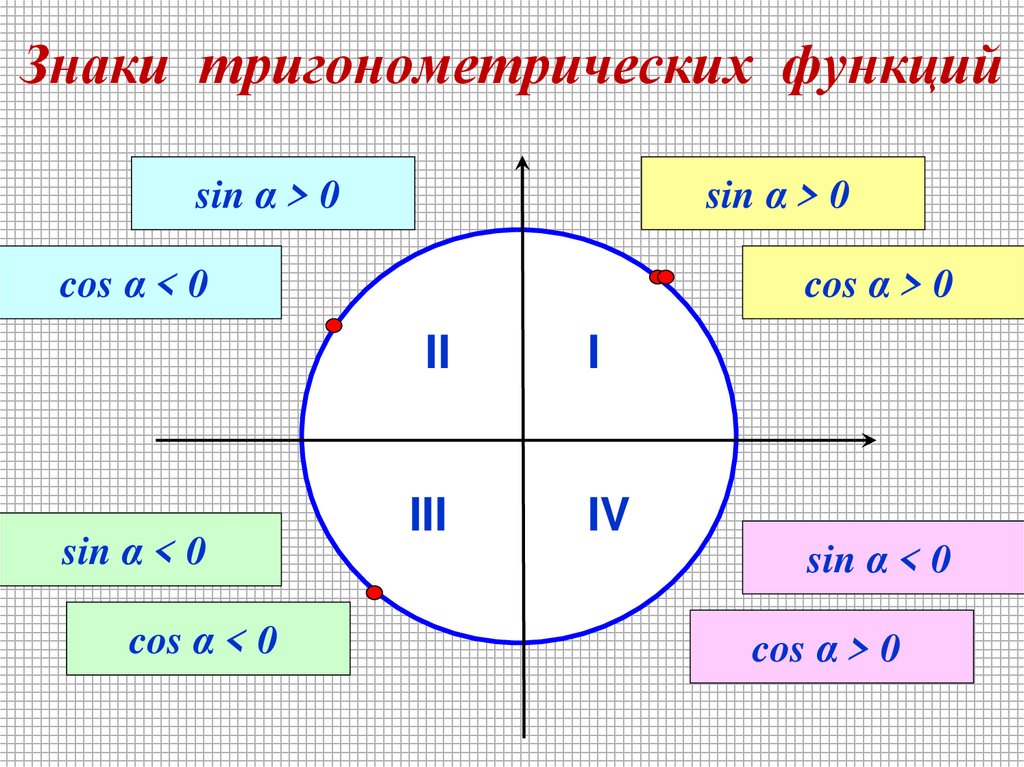
6. Знаки тригонометрических функций
sin α > 0sin α > 0
cos α < 0
cos α > 0
II
sin α < 0
cos α < 0
III
I
IV
sin α < 0
cos α > 0
7. Итак,
мы получили некоторое представлениео тригонометрических функциях
числового аргумента:
s sin t
s tg t
s cos t
s ctg t
8.
Есть целый ряд соотношений,связывающих значения различных
тригонометрических функций
sin t cos t 1
2
2
sin t
tgt
при t к
cos t
2
cos t при t к
ctgt
sin t
9.
Есть целый ряд соотношений,связывающих значения различных
тригонометрических функций
tgt ctgt 1
при t
к
2
10.
Пример 1. Упростите выражение :а)1 tg t
2
б )1 сtg t
2
11.
Ещё две формулы:1
1 tg t
при t к
2
cos t
2
1
2
1 сtg t
при t к
2
sin t
2
ВСЮДУ к z
12. Пример 2.
3Известно, что sin t и 0 t .
5
2
Найдите соответствующие значения cost ,
tgt, ctgt.
13. Пример 3.
5и t .
Известно, что tgt
12
2
Найдите соответствующие значения cost ,
sin t , ctgt.




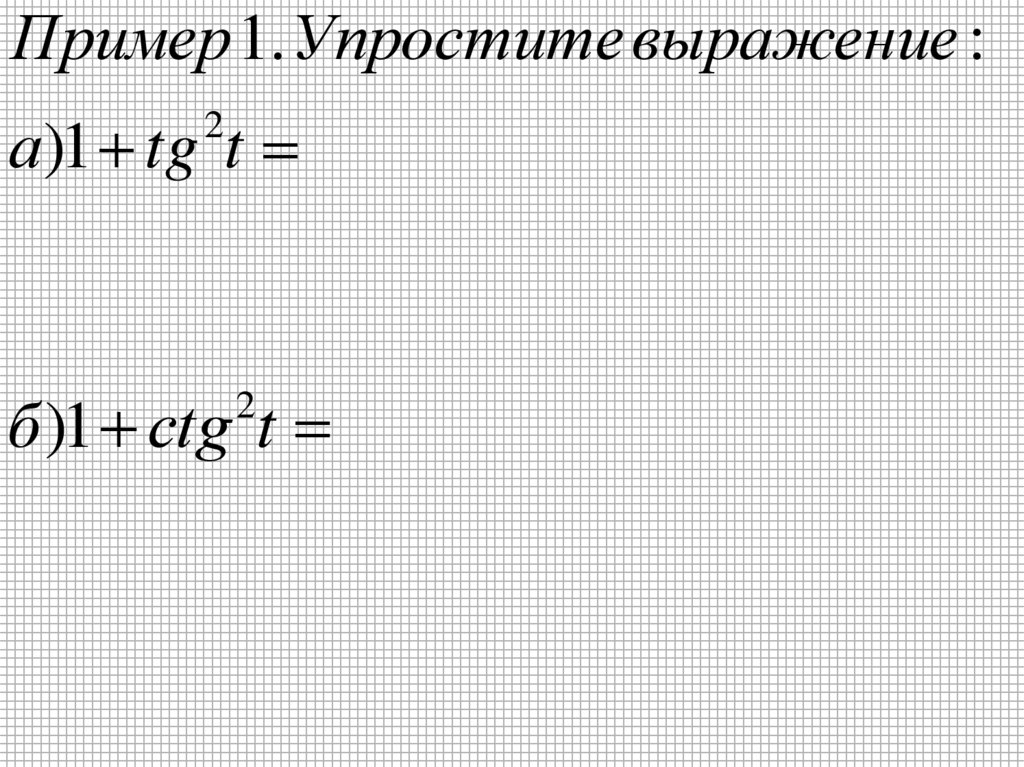



 mathematics
mathematics








