Численное моделирование сечений скалярных полей на конечно-элементных сетках

1. Выпускная квалификационная работа бакалавра на тему: «Численное моделирование сечений скалярных полей на конечно-элементных

Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Московский государственный технический университет имени Н.Э. Баумана
(национальный исследовательский институт)»
(МГТУ им. Н.Э. Баумана)
Факультет «Фундаментальные науки» (ФН)
Кафедра «Вычислительная математика и математическая физика» (ФН-11)
Направление 02.03.01 «Математика и компьютерные науки»
Выпускная квалификационная работа бакалавра
на тему:
«Численное моделирование сечений скалярных полей на конечноэлементных сетках с помощью интерполяционных методов»
Выполнил: студент группы ФН11-81Б Федотов Д.Ю.
Научный руководитель: ст. преп-ль кафедры ФН-11 Гумиргалиев Т.Р.
Москва, 2022

2. Концептуальная постановка задачи

• Физические процессы в сплошных средах представимы в виде изменений
физических полей некоторых величин: температуры, деформации и т.д.
• Сечения полей позволяет получить «срез» данных полей в непосредственно
интересующей нас области.
• Преимущества использования сечений:
o быстрая оценка результатов без необходимости повторного решения
задачи;
o удобное визуальное представление облегчает восприятие;
Визуализация распределения поля магнитной
индукции B в катушке
o возможность дальнейшей работы с областью;
o в
перспективе
построение
пересечений/включений
результатов.
сложных
нескольких
тел
(криволинейных)
и
анализ
сечений/
полученных
2

3. Цель и задачи

• Цель:
o разработать алгоритм численного моделирования плоских сечений скалярных полей на конечно-элементных
сетках с использованием интерполяционных методов.
• Задачи:
o изучить интерполяционные методы;
o разработать алгоритм построения плоских сечений конечных элементов и сеток;
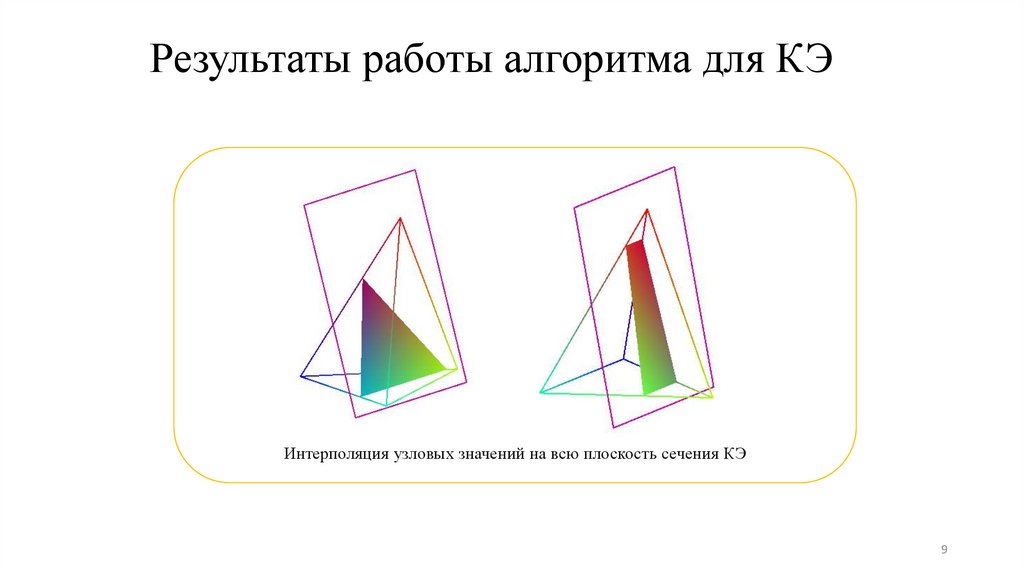
o интерполировать значения заданного скалярного поля на плоскость сечения;
o визуализировать полученные результаты;
o оптимизировать работу алгоритма для сеток больших размеров.
3

4. Интерполяция

• Интерполяцией называют приближение табличной функции