Демографический анализ. Смертность. (Лекция 3)

1. Демографический анализ

ЛЕКЦИЯ 3
СМЕРТНОСТЬ
1

2. План лекции:

1.
2.
2
Краткая история разработки таблицы смертности
Демографический метод построения таблицы
смертности

3. КРАТКАЯ ИСТОРИЯ ТАБЛИЦ СМЕРТНОСТИ

История попыток вывести закон, связывающий
возраст человека и уровень смертности
Появление аппарата таблиц смертности – результат
1.
развития математики (теории вероятностей)
2.
потребностей практики – развитие института
ренты
3.
появления данных о смертности в разных
возрастах – регистры рантье
3

4.

Запрет страхования жизни
1570 г. – Испания
1598 г. – Голландия
1681 г. – Франция
Смерть представлялась
· как небесная кара
или
· как проявление случайности
4

5. 1662 год: Джон Граунт (John Graunt)

"Естественные и политические
наблюдения, перечисленные в
прилагаемом оглавлении и сделанные
на основе бюллетеней о смертности по
отношению к управлению, религии,
торговле, росту, воздуху, болезням и
другим изменениям названного города.
Сочинение Джона Граунта гражданина
Лондона»
http://demoscope.ru/weekly/2006/0261/biblio05.php
5
(1620-1674 )

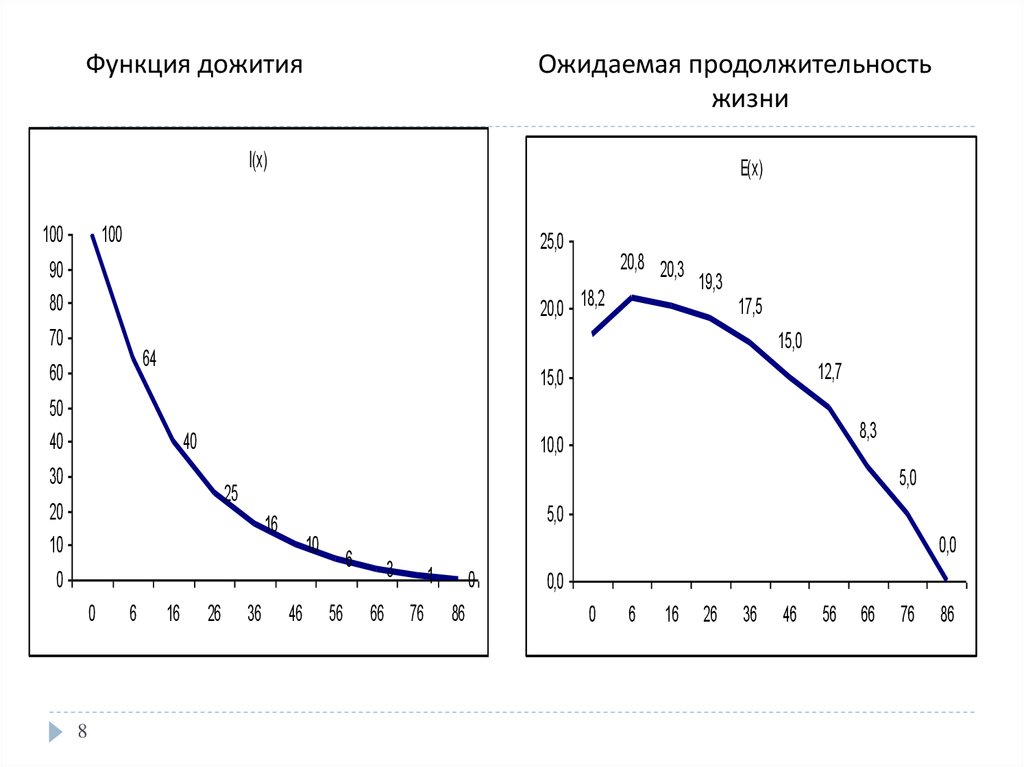
6. Граунт: идея таблицы смертности

Из 100 зачатий умирают в течение
Доживают до возраста
Первых 6 лет
36
6 лет – 64 человека
Следующих 10 лет
24
16 лет – 40
Следующих 10 лет
15
26 лет – 25
Следующих 10 лет
9
36 лет – 16
Следующих 10 лет
6
46 лет – 10
Следующих 10 лет
4
56 лет – 6
Следующих 10 лет
3
66 лет – 3
Следующих 10 лет
2
76 лет – 1
Следующих 10 лет
1
86 лет – 0
6

7. Заслуги Граунта:

Сама идея таблицы: сопоставление возраста и чисел
умирающих
Придумал корень таблицы – 100 зачатий
Вывел понятие частоты и средней
Впервые проанализировал качество данных
Впервые осуществил:
- анализ роста численности населения;
- сравнение численности населения Лондона и Парижа;
- оценку численности населения Англии;
- анализ частоты убийств;
- анализ летальности хронических болезней;
- анализ смертности при родах и пр.
7

8.

Функция дожития
Ожидаемая продолжительность
жизни
l(x)
100
E(x)
100
25,0
90
80
20,8 20,3
20,0 18,2
70
40
5,0
25
20
10
5,0
16
10
6
0
8
16
8,3
10,0
30
6
12,7
15,0
50
40
0
17,5
15,0
64
60
19,3
26
36
46
56
0,0
3
66
1
76
0
86
0,0
0
6
16
26
36
46
56
66
76
86

9. 1680 год: Г.В. Лейбниц «Наброски некоторых новых соображений относительно человеческой жизни и числа людей» (опубликовано через 200 лет)

Каждому возрасту соотнес вероятность умереть
Рассчитал среднюю продолжительность жизни для возраста
0 лет и для х лет
Выдвинул гипотезу стационарного населения:
«рождаемость людей всегда остается постоянной и
настолько равна смертности, что общая численность людей
остается практически неизменной, и даже число людей в
каждом возрасте практически не меняется»
9

10. 1693 год: Э. Галлей доклад в Королевском обществе: «Оценка смертности человека на основе старых таблиц рождения и отпеваний г. Бреслау с попыт

1693 год: Э. Галлей
доклад в Королевском обществе:
«Оценка смертности человека на
основе старых таблиц рождения и
отпеваний г. Бреслау с попыткой
рассчитать пожизненную ренту»
Предложил Метод смертных списков для расчета
таблиц смертности:
исходный показатель – числа умирающих
Mx
d
n x
M
n
10

11.

11
Рассчитал таблицу смертности для реального закрытого
населения
Предложил идею закрытого населения:
«Изучение смертности требует, чтобы по возможности
те люди, которых мы изучаем, не мигрировали и
умирали там, где были рождены. То есть чтобы не
было ни роста населения за счет иммиграции, ни
убыли за счет эмиграции»
Предложил методы расчета страховых тарифов

12. 1842 год: У. Фарр

Предложил демографический метод
расчета таблиц смертности
(одновременно с А.Кетле)
Показал различия коэффициента
смертности и вероятности умереть,
их взаимосвязь
Сравнил коэффициенты смертности по
регионам и по профессиям
12

13. Формула Кетле-Фарра (исторически первая, положившая начало демографическому методу построения таблиц смертности), построена с допущением

Формула Кетле-Фарра (исторически первая,
положившая начало демографическому методу
построения таблиц смертности), построена с
допущением линейного изменения числа смертей в
возрастных интервалах
Однолетние
возрастные интервалы:
n-летние возрастные
интервалы:
2 1 mx
1 qx
2 1 m x
2n n mx
n qx
2 n n mx
n
qi 1
13

14. В России первые таблицы смертности, рассчитанные современным, демографическим методом, появились только в начале XX века, после переписи 1897

года,
поскольку впервые были получены
данные для расчета знаменателя
возрастных коэффициентов
смертности: nРx
14

15. Построение таблиц смертности для условного поколения

Главная проблема заключается в переходе от nmx к
nqx. Решается с помощью следующего уравнения
(Гревилл – 1943г., Чанг – 1968г.)
n n mx
q
n x
1 (n n a x ) n mx
n
15
ax
Время, прожитое до наступления смерти
умершими в возрастном интервале, или доля
возрастного интервала, прожитая до смерти
умершими в данном интервале. В формуле
Фарра-Кетле равно ½.

16. Формула Гревилла для построения кратких таблиц смертности

Одна из возможных формул перехода от nmx к nqx:
mx
n qx
1
n
n mx (0.5 ( n mx 0,095))
n
12
n
16

17. Литература:

• Денисенко М.Б., Калмыкова Н.М. Демография, раздел 3
• Preston S., Heuveline P., Guillot M. Demography: Measuring and
Modeling Population Processes, главы 2 и 3
• Дарский Л.Е., Тольц М.С. Демографические таблицы. М., 2013.
Раздел II
http://www.demoscope.ru/weekly/knigi/darskij_tolc/darskij_tolts.pdf
• The Human Mortality Database: http://www.mortality.org/
• База РЭШ http://demogr.nes.ru/index.php/ru/demogr_indicat/data
17

18. Демографический анализ

ТАБЛИЦЫ СМЕРТНОСТИ
18

19. План лекции:

1. Демографические таблицы: виды,
требования к построению
2. Таблица смертности: построение,
взаимосвязь показателей
19

20. ДЕМОГРАФИЧЕСКИЕ ТАБЛИЦЫ -

ДЕМОГРАФИЧЕСКИЕ ТАБЛИЦЫ • УПОРЯДОЧЕННЫЕ РЯДЫ ВЗАИМОСВЯЗАННЫХ
ВЕЛИЧИН, ХАРАКТЕРИЗАЮЩИХ ТЕЧЕНИЕ ОДНОГО ИЛИ
НЕСКОЛЬКИХ ДЕМОГРАФИЧЕСКИХ ПРОЦЕСОВ В
КОГОРТЕ
• ЧИСЛОВЫЕ МОДЕЛИ, ОТРАЖАЮЩИЕ
1. ИНТЕНСИВНОСТЬ ДЕМОГРАФИЧЕСКОГО ПРОЦЕССА
В ЗАВИСИМОСТИ ОТ СОБСТВЕННОГО ВРЕМЕНИ
КОГОРТЫ
2. ИЗМЕНЕНИЕ ЧИСЛЕННОСТИ САМОЙ КОГОРТЫ ПОД
ВОЗДЕЙСТВИЕМ ДЕМОГРАФИЧЕСКОГО ПРОЦЕССА
20

21. Демографические таблицы – один из наиболее распространенных видов представления демографических процессов в реальной или условной кого

Демографические таблицы – один из
наиболее распространенных видов
представления демографических процессов в
реальной или условной когорте
• XVII век – таблицы смертности (Дж.
Граунт)
• XVIII век – таблицы брачности (И.
Мюре)
• XIX век – таблицы рождаемости (Р. Бек)
21

22. Демографические таблицы

• ОБЩИЕ –
для повторяющихся
демографических событий:
• рождения
• браки
Основной показатель –
коэффициент
• СПЕЦИАЛЬНЫЕ –
для неповторяющихся
демографических
событий
• смерти
• рождения по
очередности
• браки по очередности
Основной показатель –
вероятность наступления
события

23. Демографические таблицы

• ПРОСТЫЕ –
один демографический
процесс
таблицы единственного
выбытия
(Single Decrement Table)
23
• КОМБИНИРОВАННЫЕ –
несколько демографических
процессов
таблицы
множественного
выбытия
(Multiple-Decrement Table)

24. Основные распределения любой таблицы единственного выбытия

1. распределение «доживающих» Ni, т.е. число лиц в точном возрасте i,
для которых не наступило изучаемое неповторяющееся событие
2. распределение вероятностей (рисков) i+1qi наступления события
между точными возрастами i и i+1.
e
1 qi
Ni
1 i
3. распределение неповторяющихся событий 1ei, наступивших в
возрасте i исполнившихся лет (т.е. между точными возрастами i и i+1)
e Ni Ni 1
1 i
Еще одно распределение можно вывести из предыдущих:
вероятность pi ненаступления события между точными возрастами i и
i+1:
N
1 pi
24
i 1
Ni
1 1 qi

25. ТАБЛИЦА ЕДИНСТВЕННОГО ВЫБЫТИЯ – соотношение показателей

n
qi n ei N i
N i n qi n ei
Ni n ei Ni 1
25

26. Вероятность: дополнительные замечания

Вероятность наступления события в каждом интервале
является средним (или усредненным) риском, относящимся ко
всем членам когорты, дожившим до начала данного интервала
Если население гетерогенно (неоднородно) по отношению к
изучаемому риску, то с теми, у кого более высокая
вероятностью наступления данного события, событие
случится в среднем раньше, чем с прочими.
В результате по мере отдаления от исходного события когорты
выживающие все больше будут представлять собой
индивидов с меньшим риском.
Этот процесс называют селекцией (survivor bias).
26

27. Примеры селекции Иммигранты в среднем демонстрируют лучшее состояние здоровья по сравнению с коренным населением

• Healthy migrant effect
Селективность самого процесса
иммиграции: мигрируют люди с
лучшими характеристиками
здоровья
• Salmon Bias
В старости или заболев, мигранты
возвращаются в страну
выбытия, и лучшее состояние
здоровья иммигрантов в
принимающей стране может
объясняться недорегистрацией
смертей и заболеваний
иммигрантов и, как следствие,
– более низкими
соответствующими
коэффициентами
27

28. Если имеются агрегированные данные, заранее нельзя понять, с чем связано изменение риска по мере отдаления от исходного события когорты, п

Если имеются агрегированные данные, заранее нельзя понять, с
чем связано изменение риска по мере отдаления от исходного
события когорты, поскольку возможны 2 варианта:
• влияние «возраста»,
то есть простое
отдаление от момента
исходного события
(actual duration effect)
меняет риск в когорте
• влияние селекции,
вызванное
гетерогенностью
населения
Снижение вероятности со временем может быть вызвано любым из 2х факторов.
Рост вероятности связан всегда с отдалением от исходного события (duration effect), т.к.
гетерогенность повышает сопротивляемость населения к данному риску. Чтобы
скорректировать влияние гетерогенности, нужно постараться понять ее причины и
выделить однородные подгруппы населения. Другой способ учета гетерогенности биографический анализ (event history analysis)
28

29. ТАБЛИЦА СМЕРТНОСТИ (life tables, tables de mortalité)

Числовая МОДЕЛЬ смертности реального
или условного поколения, отражающая
- общий уровень смертности
- возрастные особенности смертности
29

30. Таблицы смертности для условного и реального поколения

• Для построения таблиц смертности реального
поколения требуется собирать информацию в
течение почти 100-летнего периода, она будет
отражать закономерности вымирания
определенной когорты, но с некоторым
опозданием
• Таблицы условного поколения – оценки
смертности гипотетического поколения. Они
оперативно отражают изменение уровня
смертности во времени и влияние на смертность
30

31. При построении таблицы используется устойчивая система показателей, рекомендованная в конце XIX века Лондонским институтом актуариев

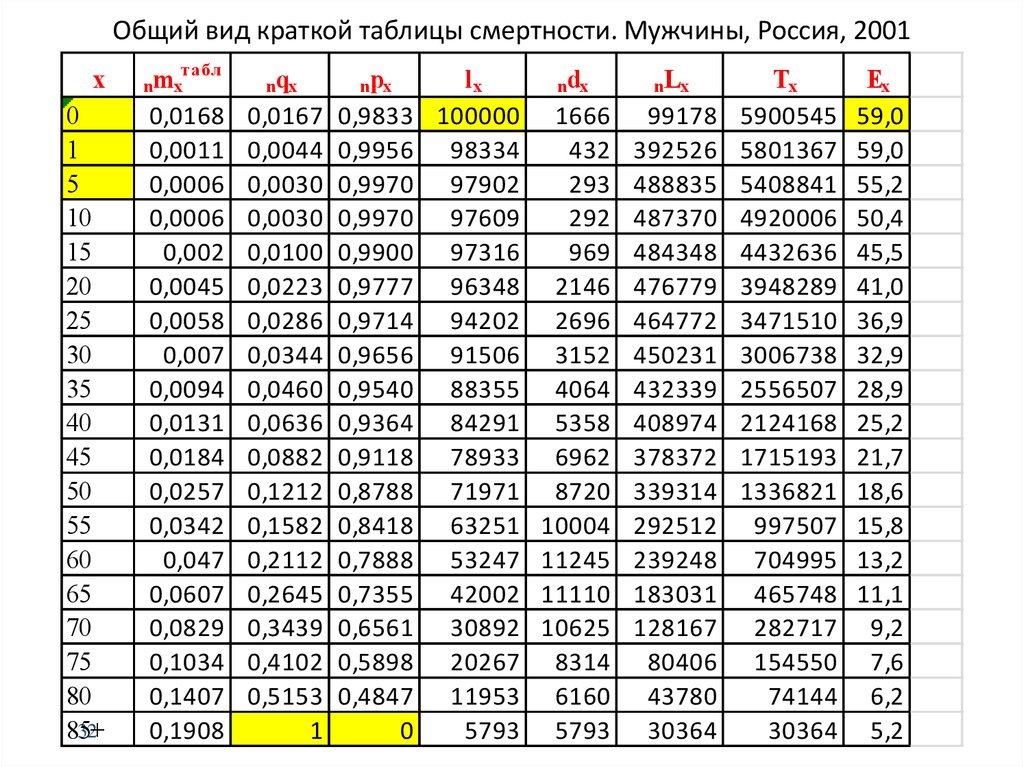
31

32. Общий вид краткой таблицы смертности. Мужчины, Россия, 2001

х
табл
nmx
nqx
npx
0
1
5
10
15
20
25
30
35
40
45
50
55
60
65
70
75
80
32
85+
0,0168
0,0011
0,0006
0,0006
0,002
0,0045
0,0058
0,007
0,0094
0,0131
0,0184
0,0257
0,0342
0,047
0,0607
0,0829
0,1034
0,1407
0,1908
0,0167
0,0044
0,0030
0,0030
0,0100
0,0223
0,0286
0,0344
0,0460
0,0636
0,0882
0,1212
0,1582
0,2112
0,2645
0,3439
0,4102
0,5153
1
0,9833
0,9956
0,9970
0,9970
0,9900
0,9777
0,9714
0,9656
0,9540
0,9364
0,9118
0,8788
0,8418
0,7888
0,7355
0,6561
0,5898
0,4847
0
lx
100000
98334
97902
97609
97316
96348
94202
91506
88355
84291
78933
71971
63251
53247
42002
30892
20267
11953
5793
ndx
nLx
1666
432
293
292
969
2146
2696
3152
4064
5358
6962
8720
10004
11245
11110
10625
8314
6160
5793
99178
392526
488835
487370
484348
476779
464772
450231
432339
408974
378372
339314
292512
239248
183031
128167
80406
43780
30364
Tx
5900545
5801367
5408841
4920006
4432636
3948289
3471510
3006738
2556507
2124168
1715193
1336821
997507
704995
465748
282717
154550
74144
30364
Еx
59,0
59,0
55,2
50,4
45,5
41,0
36,9
32,9
28,9
25,2
21,7
18,6
15,8
13,2
11,1
9,2
7,6
6,2
5,2

33. ШКАЛА ТАБЛИЦЫ

х
• Единственная независимая переменная,
которая как правило измеряется в годах, но
может измеряться в днях, месяцах (например,
при изучении младенческой смертности)
• Шкала таблицы: время, прошедшее с момента
формирования когорты (от исходного события)
• В зависимости от шага шкалы (длины
возрастного интервала) таблицы бывают:
- полные (шаг = 1 году)
- краткие (шаг = 5 или 10 годам)
33

34. КОРЕНЬ ТАБЛИЦЫ

l0
Все показатели таблицы рассчитываются в
едином масштабе.
Масштаб задается КОРНЕМ ТАБЛИЦЫ –
условной исходной численностью когорты
(число родившихся). Обычно 100 000
человек.
34

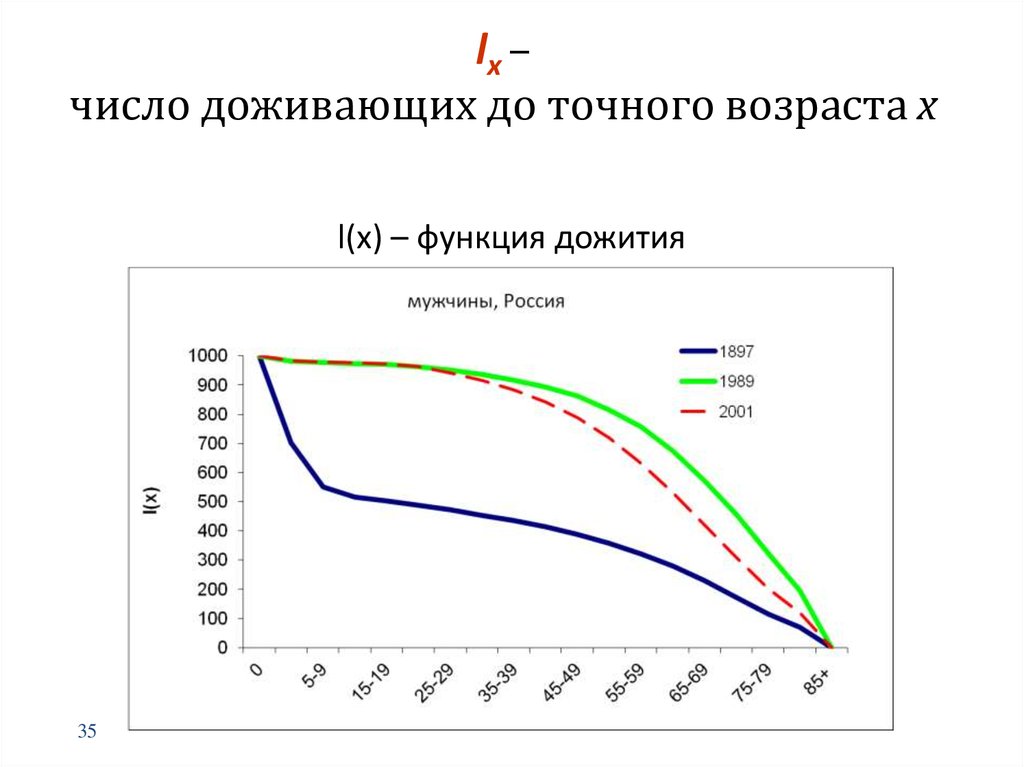
35. lx – число доживающих до точного возраста х

l(x) – функция дожития
35

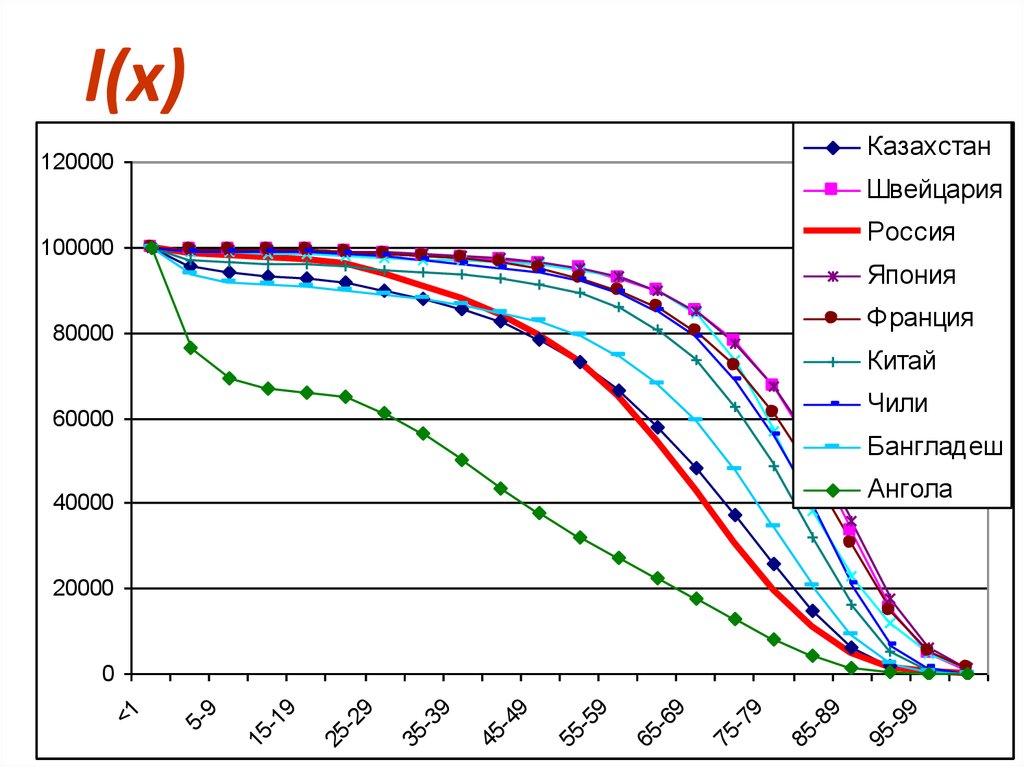
36. l(x)

Казахстан
120000
Швейцария
Россия
100000
Япония
Франция
80000
Китай
Чили
60000
Бангладеш
Ангола
40000
20000
95
-9
9
85
-8
9
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
59
36
<1
0

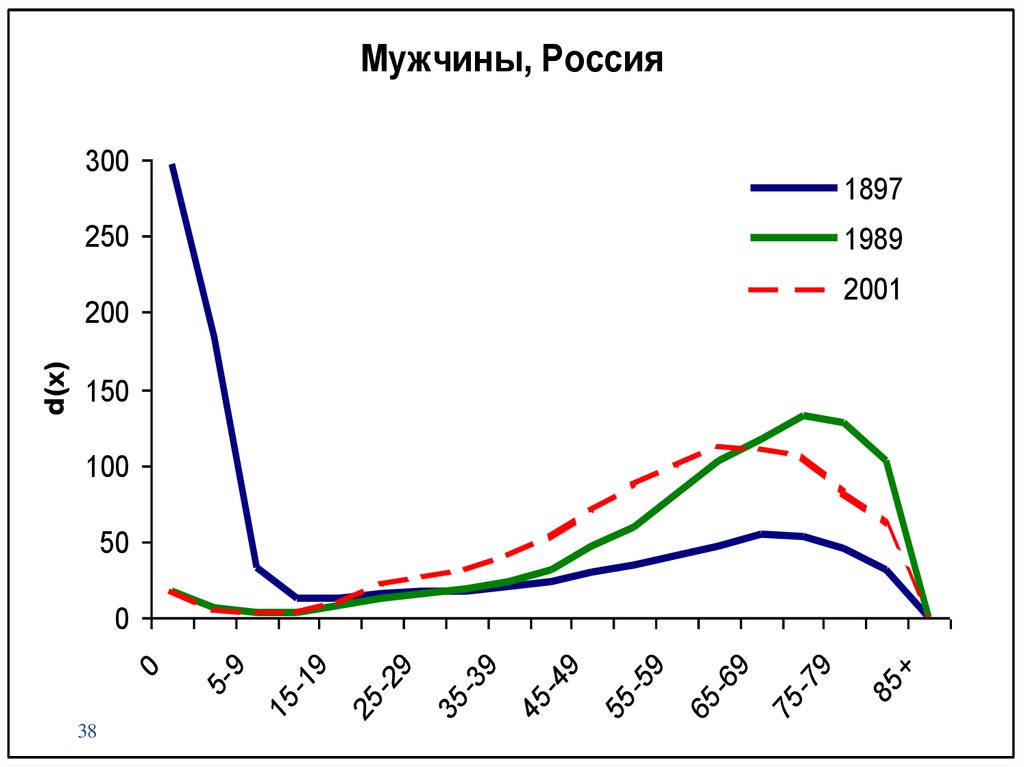
37. ndx – число умирающих в интервале возраста от x до x+n

– число умирающих в
интервале возраста от x до x+n
l n d x lx n
ndx
x
n
d x lx lx n
w
0
37
n
d x l0

38.

Мужчины, Россия
300
1897
250
1989
2001
150
100
50
38
85
+
65
-6
9
75
-7
9
55
-5
9
35
-3
9
45
-4
9
25
-2
9
15
-1
9
59
0
0
d(x)
200

39. d(x)

Казахстан
25000
Швейцария
Россия
20000
Япония
Франция
15000
Китай
Чили
Ангола
10000
5000
39
95
-9
9
85
-8
9
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
59
<1
0

40. npx- вероятность выжить в интервале возраста от х до x+n nqx- вероятность умереть в интервале возраста от х до x+n

lx
n
qx
lx n
lx lx n n d x
n px n q x
lx
lx
lx
1 n p x n q x
40

41.

nmx
– табличный
коэффициент смертности
в интервале возраста от x
до x+n
dx
n mx
n Lx
n
Величина коэффициента не
зависит от длины
возрастного интервала
41
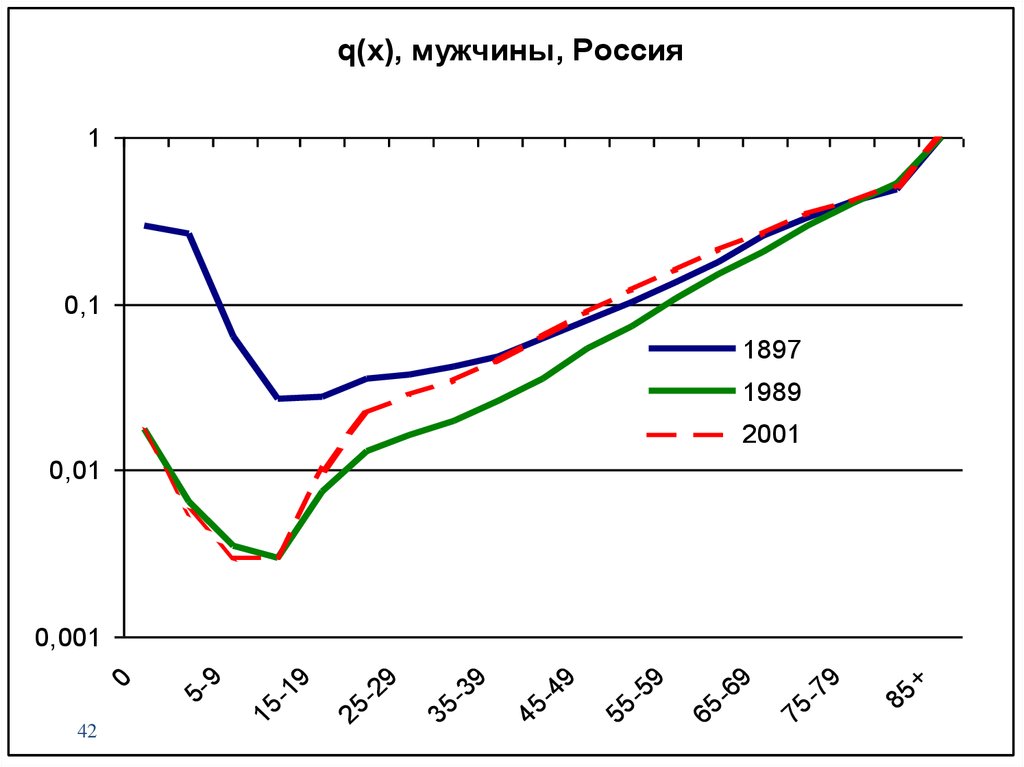
nqx
– вероятность умереть
в интервале возраста
от x до x+n
dx
n qx
lx
n
Величина вероятности
зависит от длины
возрастного интервала

42.

q(x), мужчины, Россия
1
0,1
1897
1989
2001
0,01
85
+
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
42
59
0
0,001

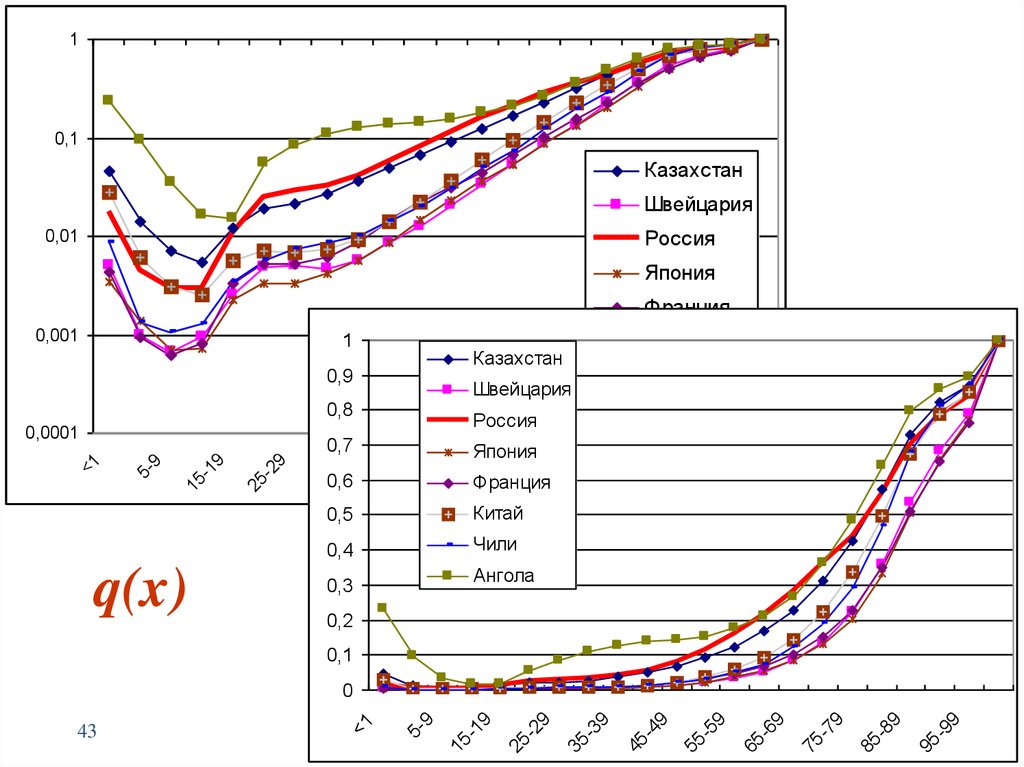
43.

1
0,1
Казахстан
Швейцария
Россия
0,01
Япония
Франция
1
Казахстан
0,9
Швейцария
0,8
0,4
Чили
95
-9
9
Китай
55
-5
9
0,5
85
-8
9
Франция
Ангола
45
-4
9
55
-5
9
45
-4
9
35
-3
9
0,6
Япония
Чили
75
-7
9
q(x)
25
-2
9
15
-1
9
59
<1
0,7
Китай
35
-3
9
0,0001
Россия
65
-6
9
0,001
Ангола
0,3
0,2
0,1
95
-9
9
85
-8
9
75
-7
9
65
-6
9
25
-2
9
15
-1
9
59
43
<1
0

44. nLx – 1. Число человеко-лет, прожитых в интервале возраста от x до x+n теми, кто дожил до начала этого интервала 2. Число живущих в интервале возр

nLx
–
1. Число человеко-лет, прожитых в
интервале возраста от x до x+n теми, кто
дожил до начала этого интервала
2. Число живущих в интервале возраста
от x до x+n в стационарном населении
Упрощенная формула для гипотезы равномерного распределении
смертей в возрастном интервале от x до x+n:
44
lx lx n
L
n
n x
2

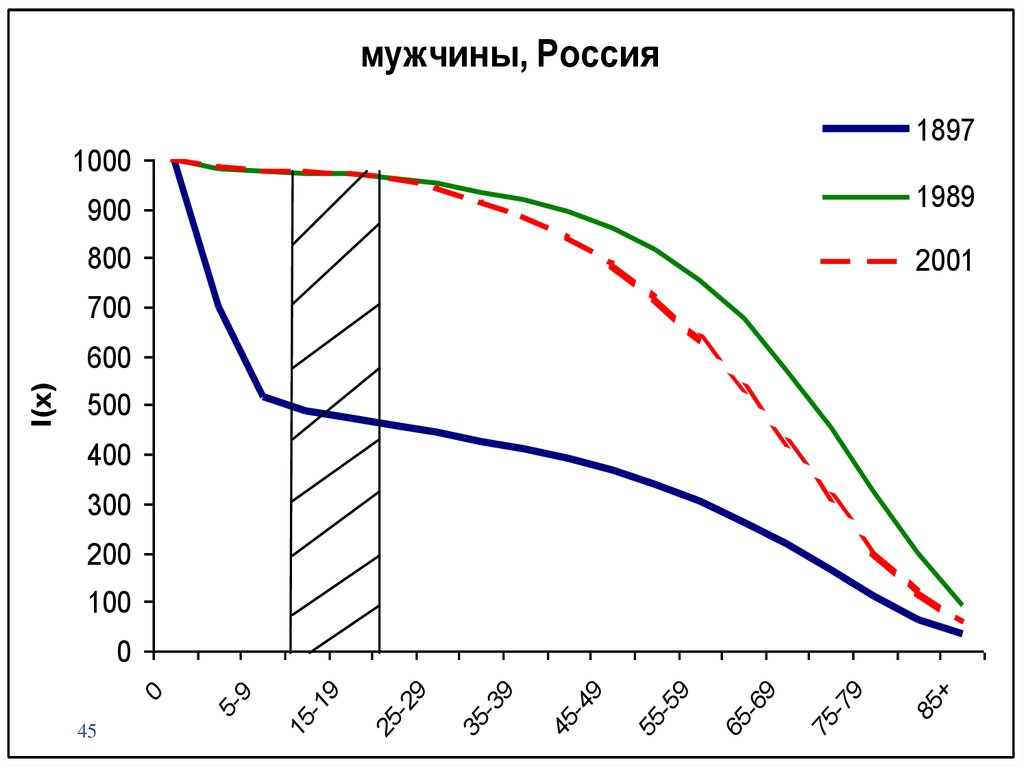
45.

мужчины, Россия
1897
1000
900
1989
800
2001
700
500
400
300
200
100
85
+
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
45
59
0
0
l(x)
600

46. Тx – Число человеко-лет жизни, которые предстоит прожить от возраста x до w (предельного возраста таблицы) тем, кто дожил до возраста х

Т х Lx Lx 1 ... Lx n ... Lw
w
Tx Lx
x
46
l(x)

47. «Закрытие» таблицы смертности: последний интервал таблицы

Пусть возраст начала последнего интервала
таблицы равен а (в нашем примере а=85).
В последнем интервале таблицы вероятность
умереть равна 1:
qа 1
Поскольку число умерших в последнем интервале равно
числу доживших до его начала, то число человеко-лет
жизни в этом интервале равно:
dа
Lа
ma
47
lа
Т a
ma

48. Еx – ожидаемая продолжительность жизни в возрасте x

w
w
n
n Lx
n dx (x )
Тх
2
x
x
Ех
lx
lx
lx
48

49. Е(х)

80
Казахстан
70
Швейцария
Россия
60
Япония
50
Франция
40
Китай
Чили
30
Ангола
20
10
49
95
-9
9
85
-8
9
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
59
<1
0

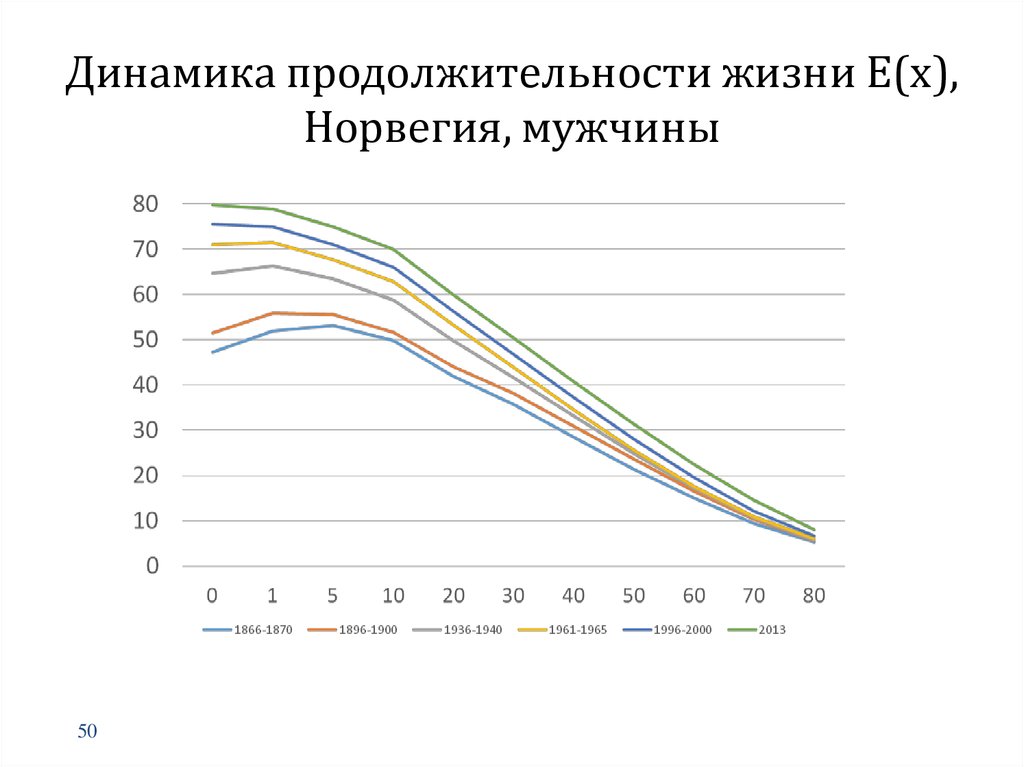
50. Динамика продолжительности жизни Е(х), Норвегия, мужчины

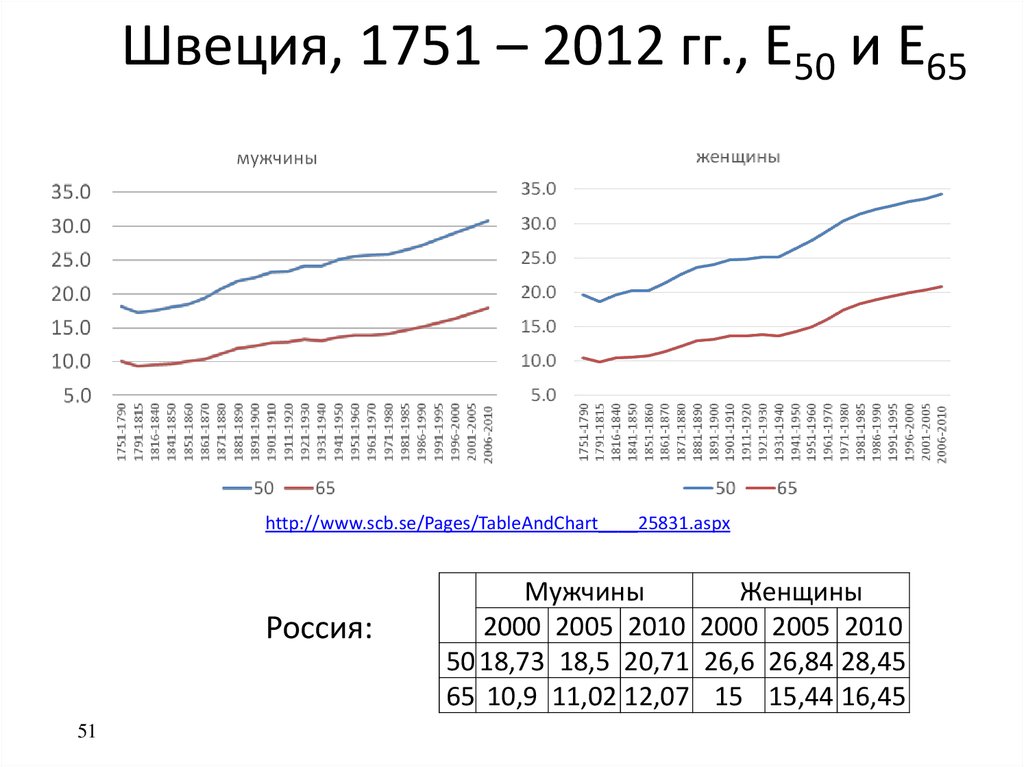
50

51. Швеция, 1751 – 2012 гг., Е50 и Е65

http://www.scb.se/Pages/TableAndChart____25831.aspx
Россия:
51
Мужчины
Женщины
2000 2005 2010 2000 2005 2010
50 18,73 18,5 20,71 26,6 26,84 28,45
65 10,9 11,02 12,07 15 15,44 16,45

52. Е0 – ожидаемая продолжительность жизни при рождении

Т0
Е0
l0
Для реального поколения:
Среднее число лет, которое прожили
лица, родившиеся в определенном году
(или временном периоде) = Средний
возраст смерти
Для условной когорты:
Среднее число лет, которое предстоит
прожить новорожденному данного года,
ЕСЛИ на протяжении всей жизни его
поколения сохранится данный порядок
вымирания (или данная таблица
смертности)
52

53. Динамика Е0 в России, 1965 – 2012 гг.

53

54.

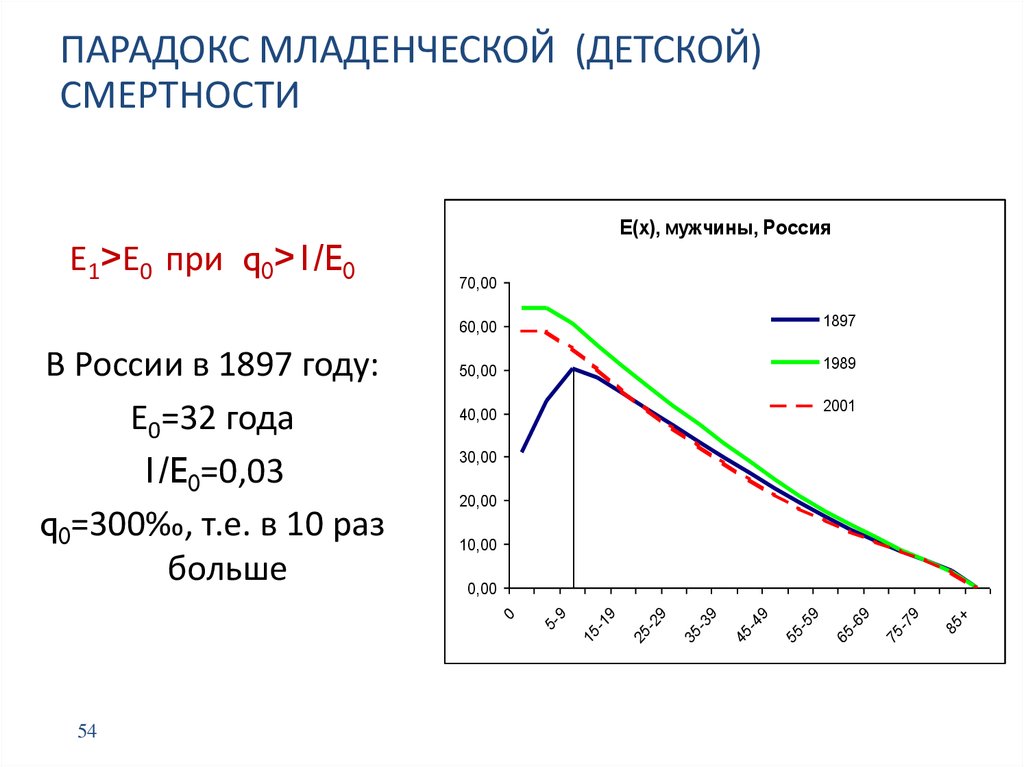
ПАРАДОКС МЛАДЕНЧЕСКОЙ (ДЕТСКОЙ)
СМЕРТНОСТИ
60,00
1897
50,00
1989
54
2001
40,00
30,00
20,00
10,00
85
+
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
0,00
0
В России в 1897 году:
Е0=32 года
1/E0=0,03
q0=300‰, т.е. в 10 раз
больше
70,00
59
Е1>Е0 при q0>1/E0
Е(х), мужчины, Россия

55. Отличие Е0 от среднего возраста смерти в данном году

Е0
1. Не зависит от возрастной
структуры населения
nPx
2. Зависит от порядка
вымирания, т.е. nmx
Средний возраст
умерших
1. Зависит от возрастной
структуры населения nPx
2. Зависит от порядка
вымирания nmx
w
w
w
n
n Lx
n dx (x )
Т0
2
Е0
0
0
l0
l0
l0
55
x
n
0 n M x ( x 2 )
w
0
n
Mx

56.

Медианная
продолжительность жизни
Для новорожденных –
возраст, до которого
доживет ровно половина
исходной численности
поколения (0,5l0)
1000
Модальная
продолжительность жизни
Значение, при котором l(x)
убывает с максимальной
скоростью, d(x) достигает
максимума.
120
900
100
800
700
80
600
60
500
400
40
300
200
20
100
85
+
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
0
85
+
75
-7
9
65
-6
9
55
-5
9
45
-4
9
35
-3
9
25
-2
9
15
-1
9
59
0
56
59
0
0

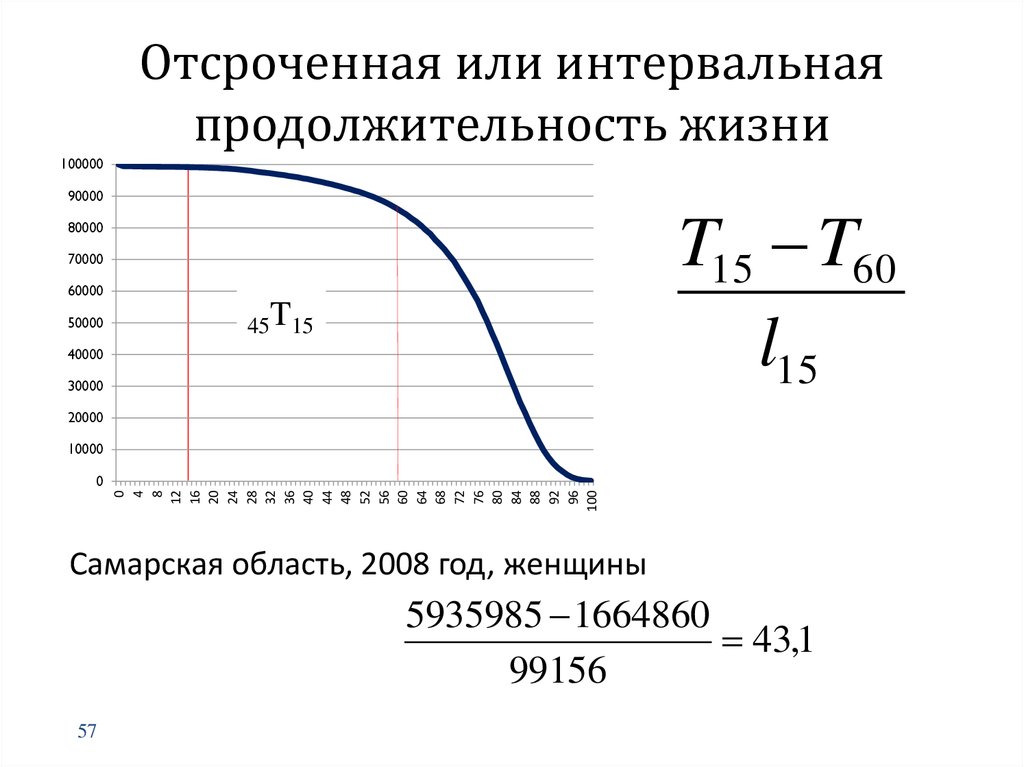
57. Отсроченная или интервальная продолжительность жизни

100000
90000
T15 T60
l15
80000
70000
60000
50000
45T15
40000
30000
20000
10000
0
4
8
12
16
20
24
28
32
36
40
44
48
52
56
60
64
68
72
76
80
84
88
92
96
100
0
Самарская область, 2008 год, женщины
5935985 1664860
43,1
99156
57

58. Таблица смертности для календарного года строится на основе повозрастных коэффициентов смертности, которые наблюдаются в реальном насел

Таблица смертности для календарного
года строится на основе повозрастных
коэффициентов смертности, которые
наблюдаются в реальном населении.
Эти коэффициенты смертности
преобразуют в вероятности, а затем
разворачивается вся таблица.
58

59. Литература:

• Денисенко М.Б., Калмыкова Н.М. Демография, раздел 3
• Wunsch G., Termote M. Introduction to demographic analysis.
Principles and Methods. Plenum Press, 1976. Разделы 1.2, 3.2
• Preston S., Heuveline P., Guillot M. Demography: Measuring and
Modeling Population Processes, главы 2 и 3
• Дарский Л.Е., Тольц М.С. Демографические таблицы. М., 2013.
Раздел II
http://www.demoscope.ru/weekly/knigi/darskij_tolc/darskij_tolts.pdf
• The Human Mortality Database: http://www.mortality.org/
59