Система демографических показателей

1. Введение в Демографический анализ

ВВЕДЕНИЕ В
ДЕМОГРАФИЧЕСКИЙ
АНАЛИЗ
Система показателей

2.

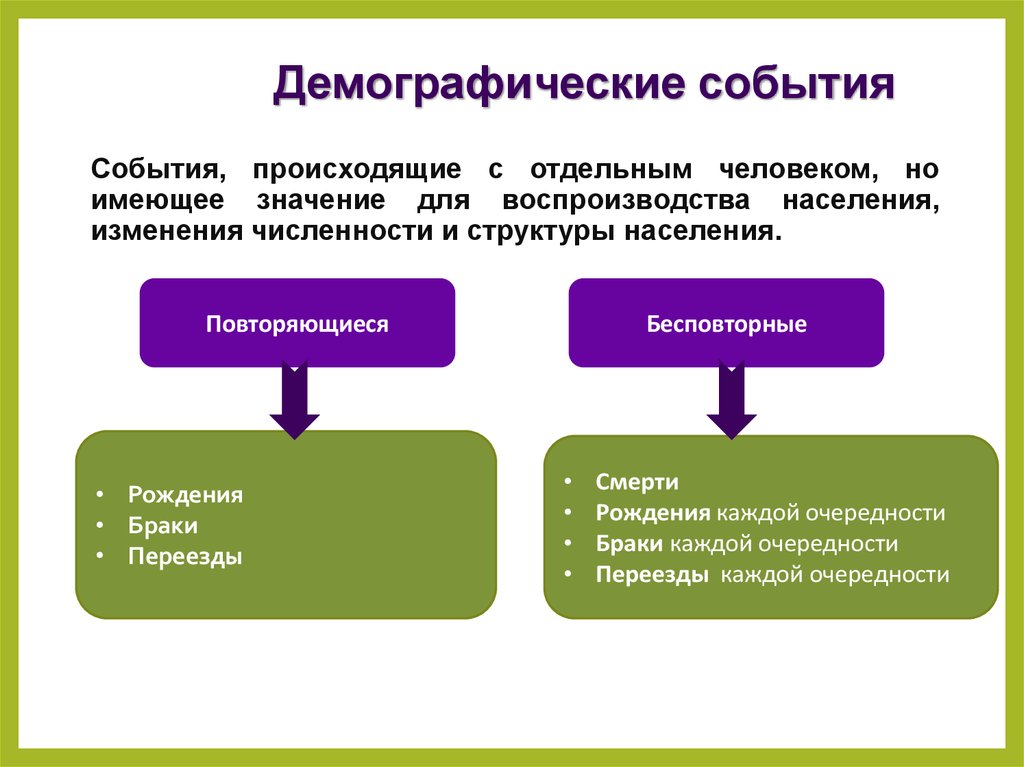
Демографические события
События, происходящие с отдельным человеком, но
имеющее значение для воспроизводства населения,
изменения численности и структуры населения.
Повторяющиеся
• Рождения
• Браки
• Переезды
Бесповторные
Смерти
Рождения каждой очередности
Браки каждой очередности
Переезды каждой очередности

3.

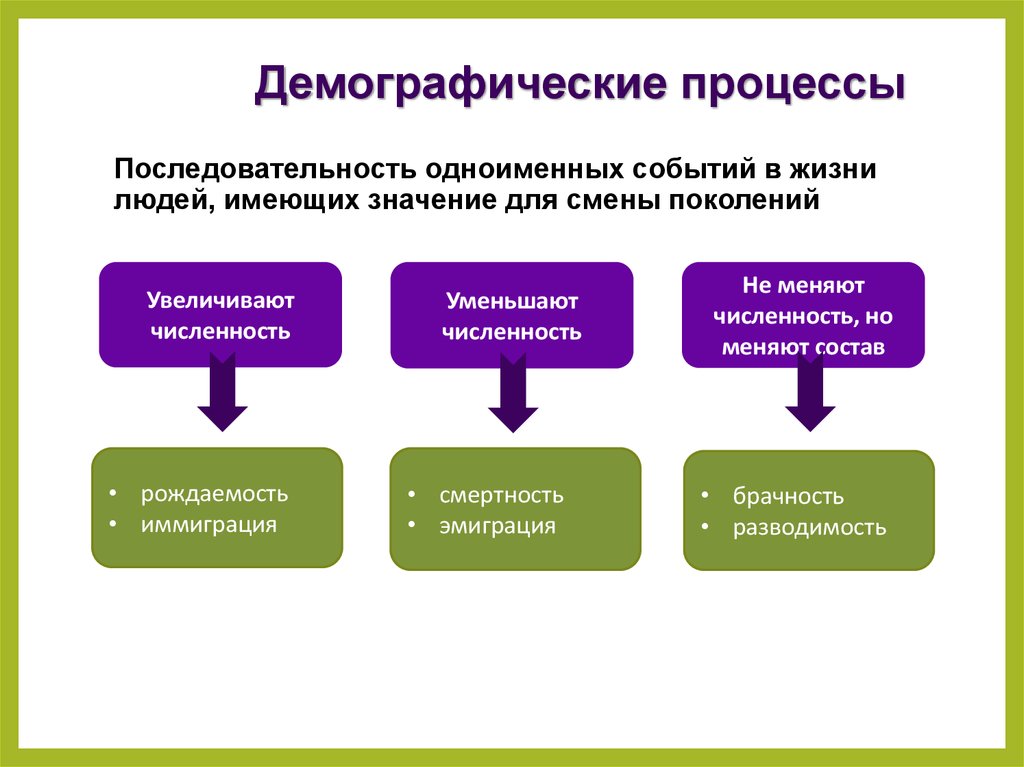
Демографические процессы
Последовательность одноименных событий в жизни
людей, имеющих значение для смены поколений
Увеличивают
численность
• рождаемость
• иммиграция
Уменьшают
численность
• смертность
• эмиграция
Не меняют
численность, но
меняют состав
• брачность
• разводимость

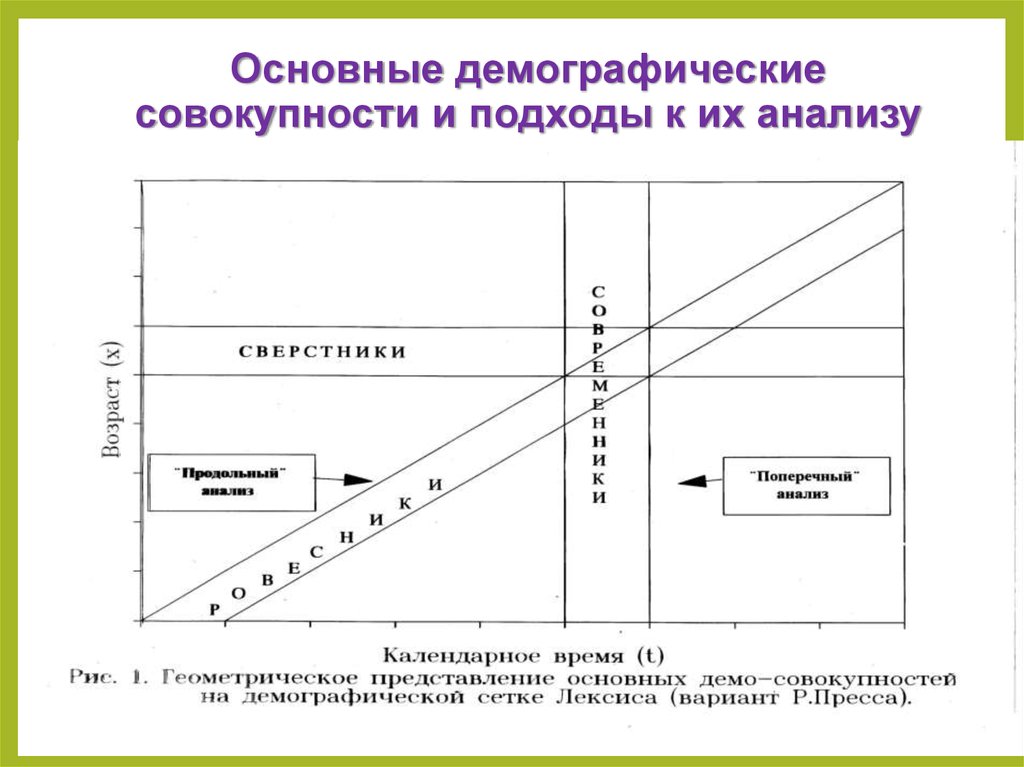
4. Основные демографические совокупности и подходы к их анализу

5. Система демографических показателей

- абсолютные показатели (число событий);
- показатели интенсивности демографического
процесса (частота наступления событий);
- показатели календаря демографического
процесса (время/возраст наступления событий и длина
интервалов времени между повторяющимися событиями) ;
- стандартизованные коэффициенты;
- показатели вероятностных демографических
таблиц смертности, рождаемости, брачности,
разводимости и др. (основанных на функциях
вероятности «дожития» в том или ином состоянии,
меняющихся со временем/возрастом.

6. АБСОЛЮТНЫЕ ПОКАЗАТЕЛИ

S – абсолютная численность населения
nSx – абсолютная численность населения в
интервале возраста от х до х+n
N – абсолютное число родившихся
M – абсолютное число умерших
nMx – абсолютное число умерших в интервале
возраста от х до х+n
B – абсолютное число браков
nBx – абсолютное число браков в интервале
возраста от х до х+n
V+ – абсолютное число въехавших на данную
территорию
+
n V x – абсолютное число въехавших на данную
территорию в интервале возраста от х до х+n

7. УРАВНЕНИЕ ДЕМОГРАФИЧЕСКОГО БАЛАНСА

S(t) = S(0) + N – M + V+ – V(N – M) – естественный прирост (ЕП)
(V+ – V- ) - миграционный прирост (МП)
S(t) - S(0) - общий прирост численности
населения за период времени t (ОП)
S(t) - S(0)= (N – M) + (V+ – V- )

8. УРАВНЕНИЕ ДЕМОГРАФИЧЕСКОГО БАЛАНСА С УЧЕТОМ ВОЗРАСТНЫХ ГРУПП

Sх(t) = Sх-t (0) – Mх-t + V+х-t – V-х-t

9.

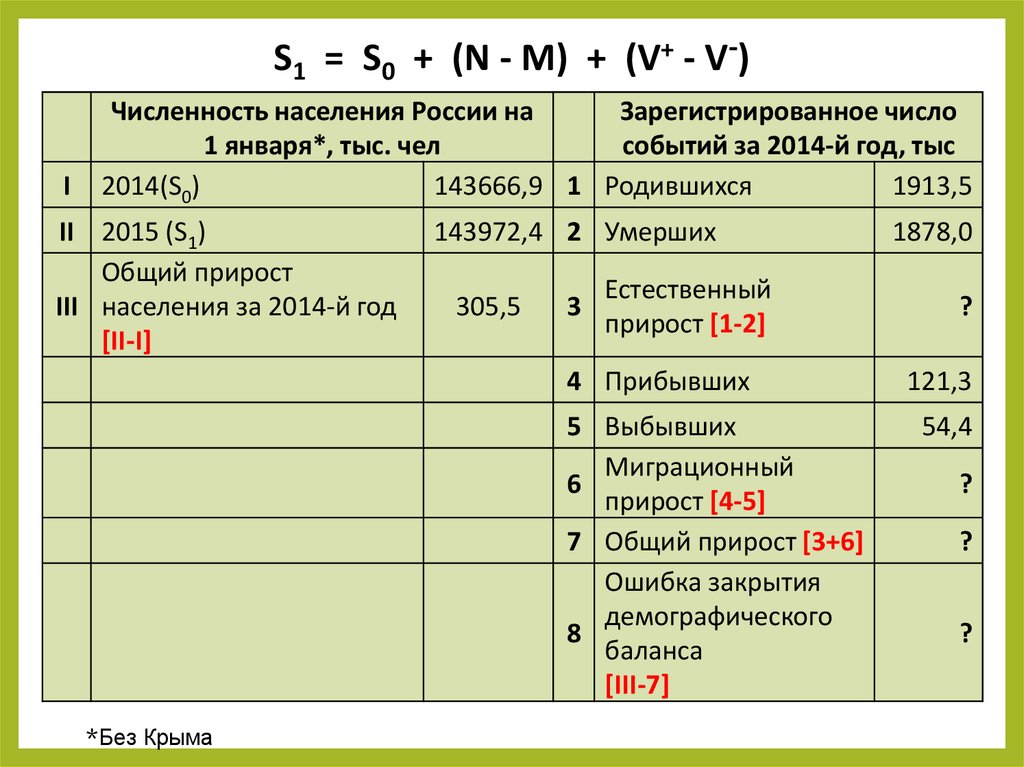
S1 = S0 + (N - M) + (V+ - V-)
I
Численность населения России на
Зарегистрированное число
1 января*, тыс. чел
событий за 2014-й год, тыс
2014(S0)
143666,9 1 Родившихся
1913,5
II 2015 (S1)
Общий прирост
III населения за 2014-й год
[II-I]
143972,4 2 Умерших
305,5
3
Естественный
прирост [1-2]
4 Прибывших
5 Выбывших
Миграционный
6
прирост [4-5]
7 Общий прирост [3+6]
Ошибка закрытия
демографического
8
баланса
[III-7]
*Без Крыма
1878,0
?
121,3
54,4
?
?
?

10. Почему абсолютными значениями следует с осторожностью использовать в сравнительных целях?

Россия
1926 год
1996 год
Число смертей, M
1920 тыс.
2082 тыс.
Численность
населения, S
Общий коэффициент
смертности, m
92,7 млн.
147,9 млн.
20,7‰
14,2 ‰

11.

Коэффициенты
t = (e / S *T) *1000
t – коэффициент, который требуется рассчитать;
e – число демографических событий;
S – средняя численность населения за период;
T – длительность наблюдаемого периода;
S *T – среднее число человеко-лет прожитое населением в данном
временном интервале;
Чаще всего (но не всегда!!!) измеряется в проми́лле (лат. per mille — на
тысячу) — одна тысячная доля, 1/10 процента; обозначается (‰)

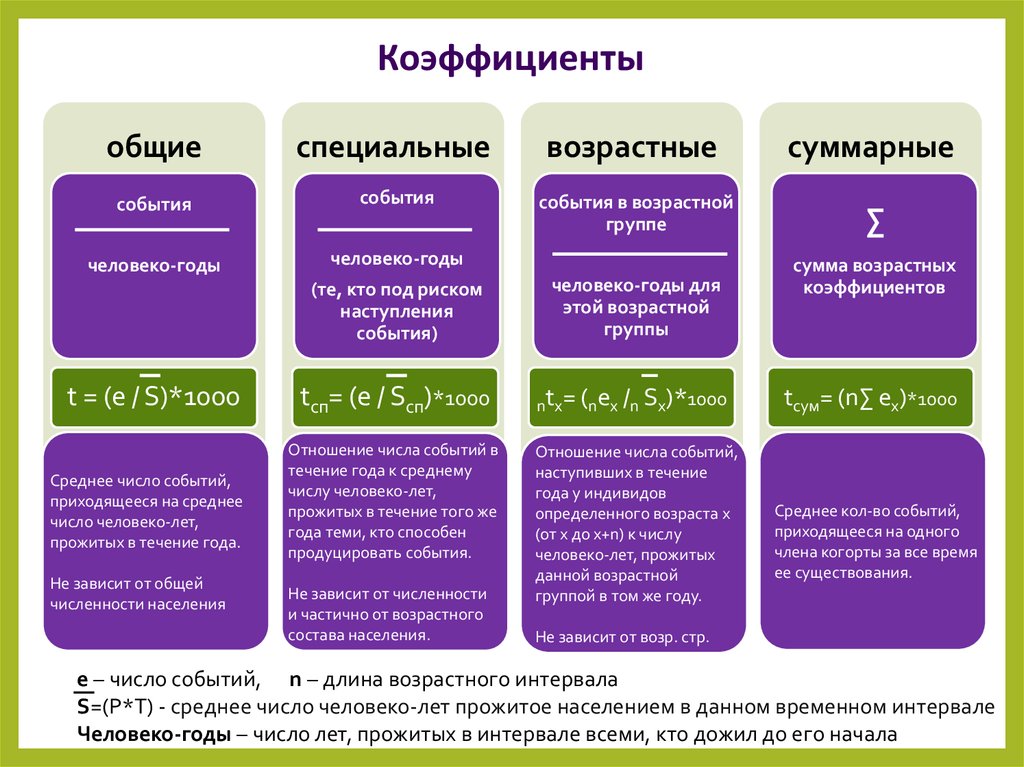
12.

Коэффициенты
общие
специальные
возрастные
суммарные
события
события
события в возрастной
группе
∑
человеко-годы
человеко-годы
t = (e / S)*1000
Среднее число событий,
приходящееся на среднее
число человеко-лет,
прожитых в течение года.
Не зависит от общей
численности населения
(те, кто под риском
наступления
события)
человеко-годы для
этой возрастной
группы
tсп= (e / Sсп)*1000
ntx= (nex /n Sx)*1000
Отношение числа событий в
течение года к среднему
числу человеко-лет,
прожитых в течение того же
года теми, кто способен
продуцировать события.
Отношение числа событий,
наступивших в течение
года у индивидов
определенного возраста х
(от х до x+n) к числу
человеко-лет, прожитых
данной возрастной
группой в том же году.
Не зависит от численности
и частично от возрастного
состава населения.
сумма возрастных
коэффициентов
tсум= (n∑ ex)*1000
Среднее кол-во событий,
приходящееся на одного
члена когорты за все время
ее существования.
Не зависит от возр. стр.
e – число событий, n – длина возрастного интервала
S=(P*T) - среднее число человеко-лет прожитое населением в данном временном интервале
Человеко-годы – число лет, прожитых в интервале всеми, кто дожил до его начала

13. Среднее число человеко-лет жизни – знаменатель любого коэффициента

В упрощенном виде рассчитывается как среднегодовая
численность населения:
S нач. S конечн .
S
2

14. ОБЩИЙ КОЭФФИЦИЕНТ – среднее число событий, приходящееся на на одного человека (на 1000 населения, на 100 000 населения и т.п.)

В общем виде как отношение:
Число событий, зарегистрированных в населении за
период времени
___________________________________
Среднее число человеко-лет, прожитых этим населением
за тот же период времени

15. Формула или определение? Формула – как рассчитать показатель Определение – что он означает

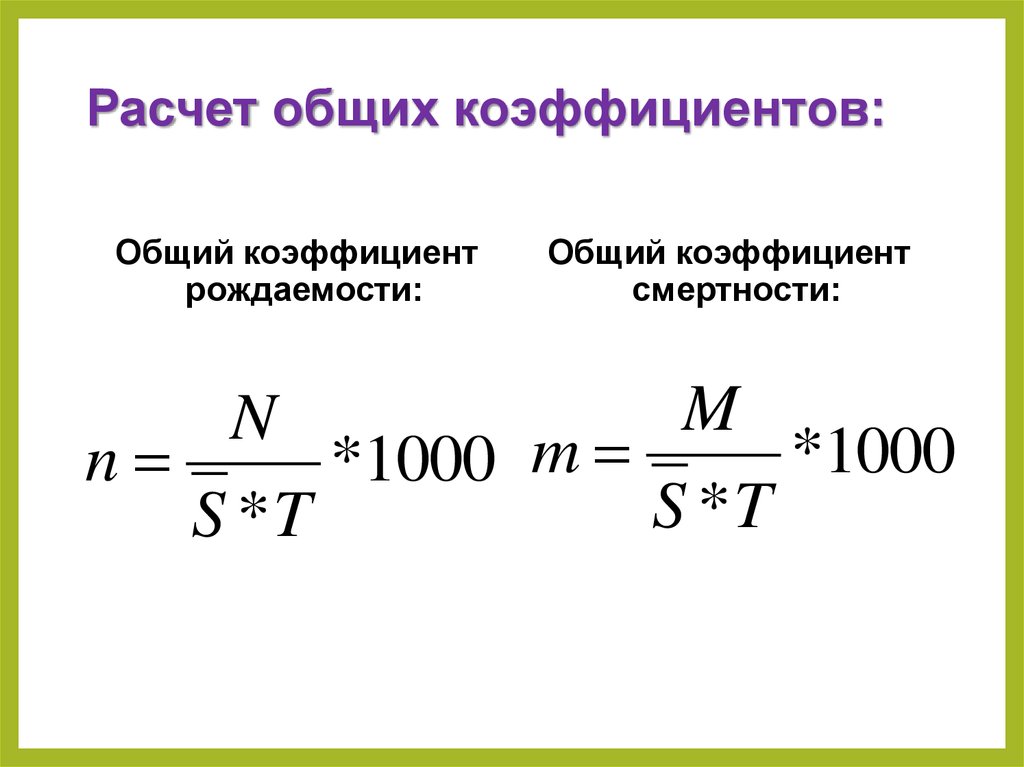
16. Расчет общих коэффициентов:

Общий коэффициент
рождаемости:
Общий коэффициент
смертности:
M
N
*1000
n
*1000 m
S *T
S *T

17. Где выше рождаемость? в Китае (16 млн. рождений ежегодно) или в Дании (64,8 тыс. рождений ежегодно)

18.

Число
рождений,
N
Численность
населения на
середину года,
S01.07.2005
Общий
коэффициент
рождаемости,
n
КИТАЙ
ДАНИЯ
16
млн.
1 303,7
млн.
64,8
тыс.
5,2
млн.
12 ‰
12 ‰

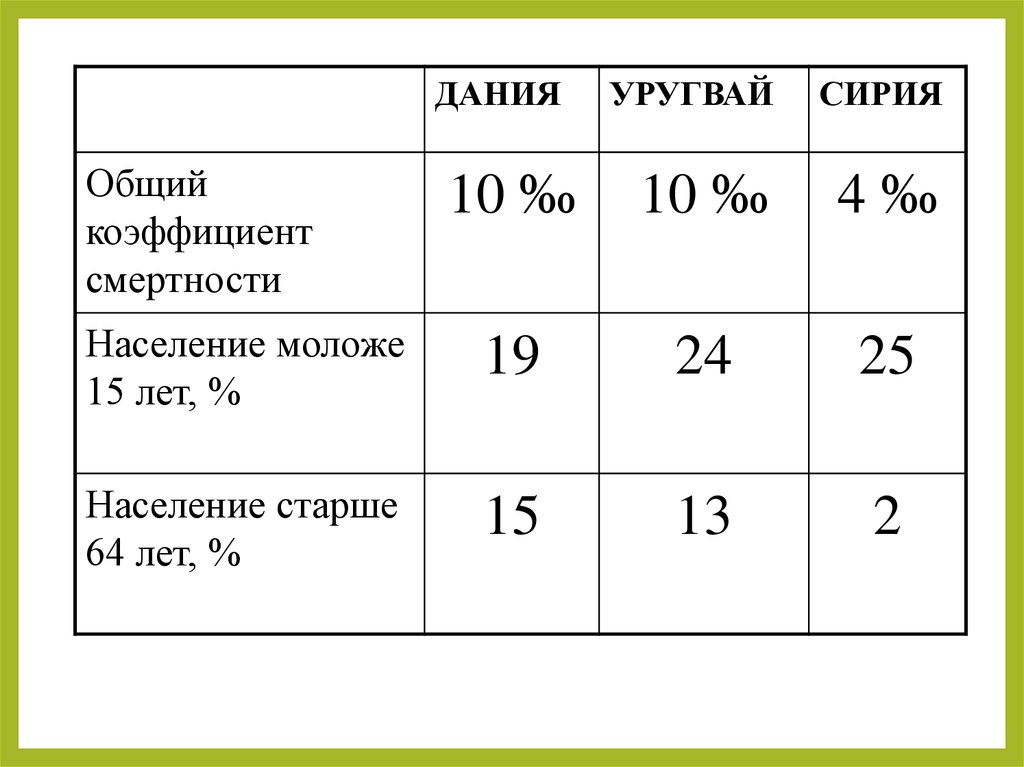
19. Где выше смертность? в Уругвае , в Сирии или в Дании ?

20.

ДАНИЯ
УРУГВАЙ
СИРИЯ
10 ‰
10 ‰
4‰
Население моложе
15 лет, %
19
24
25
Население старше
64 лет, %
15
13
2
Общий
коэффициент
смертности

21. Достоинства и недостатки общих коэффициентов

+
• НЕ
ЗАВИСЯТ ОТ
ЧИСЛЕННОСТИ
НАСЕЛЕНИЯ
• Легко рассчитать
(нужно мало данных) –
преимущество для
лентяев!!!
• СУЩЕСТВЕННО
ЗАВИСЯТ
ОТ СТРУКТУРЫ
НАСЕЛЕНИЯ И ПОЭТОМУ
ЗАЧАСТУЮ НЕПРИГОДНЫ
ДЛЯ СРАВНЕНИЯ, могут
ввести в заблуждение

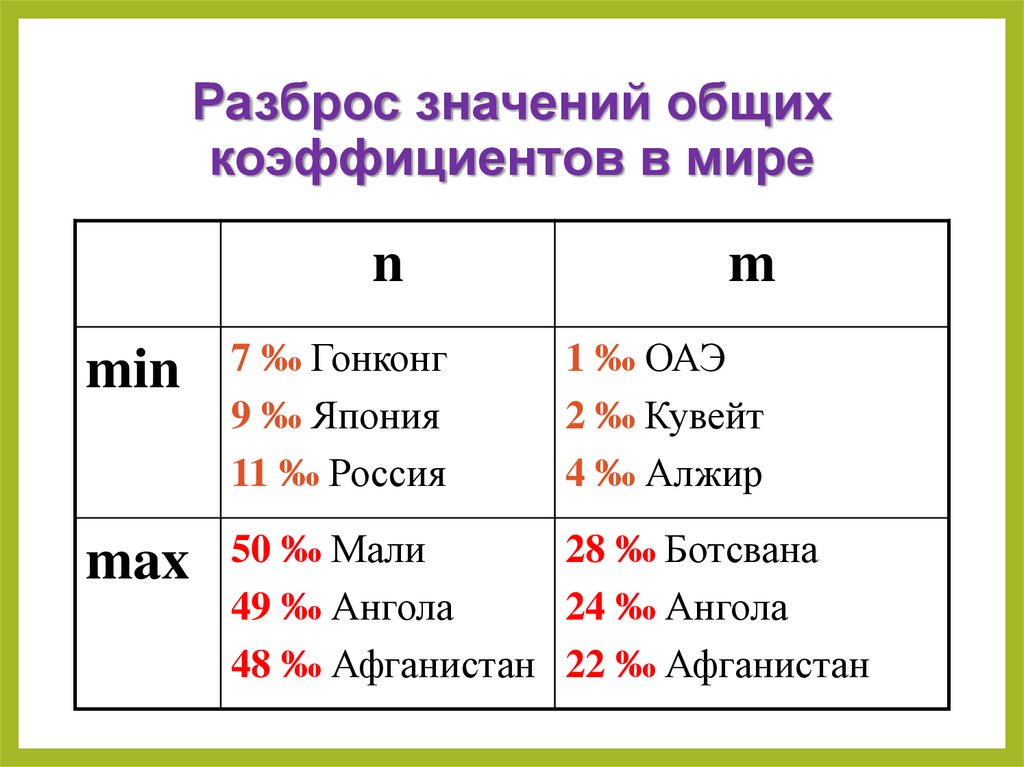
22. Разброс значений общих коэффициентов в мире

n
m
min
7 ‰ Гонконг
9 ‰ Япония
11 ‰ Россия
1 ‰ ОАЭ
2 ‰ Кувейт
4 ‰ Алжир
max
50 ‰ Мали
28 ‰ Ботсвана
49 ‰ Ангола
24 ‰ Ангола
48 ‰ Афганистан 22 ‰ Афганистан

23. ИЗБАВЛЯЕМСЯ ОТ ВЛИЯНИЯ СТРУКТУР Населения (возрастной структуры)

ИЗБАВЛЯЕМСЯ ОТ ВЛИЯНИЯ
СТРУКТУР НАСЕЛЕНИЯ
(ВОЗРАСТНОЙ СТРУКТУРЫ)
1.
2.
3.
ОБЩИЕ КОЭФФИЦИЕНТЫ
ВОЗРАСТНЫЕ И СПЕЦИАЛЬНЫЕ
КОЭФФИЦИЕНТЫ
(СУММАРНЫЕ КОЭФФИЦИЕНТЫ,
СТАНДАРТИЗОВАННЫЕ КОЭФФИЦИЕНТЫ)

24. Виды демографических процессов

СПЕЦИАЛЬНЫЙ КОЭФФИЦИЕНТ
РОЖДАЕМОСТИ – зависит от
структуры знаменателя
f спец
N
1000
f
S
T
49 15

25. СПЕЦИАЛЬНЫЙ КОЭФФИЦИЕНТ РОЖДАЕМОСТИ – зависит от структуры знаменателя

ВОЗРАСТНОЙ КОЭФФИЦИЕНТ
РОЖДАЕМОСТИ – не зависит от
возрастной структуры, особенно если
рассчитан для однолетних интервалов
n
N
n
х
fх
1000
f
S
T
n х

26. ВОЗРАСТНОЙ КОЭФФИЦИЕНТ РОЖДАЕМОСТИ – не зависит от возрастной структуры, особенно если рассчитан для однолетних интервалов

ВОЗРАСТНОЙ КОЭФФИЦИЕНТ
СМЕРТНОСТИ
M
n
х
m
1000
n
х
S
T
n х

27. ВОЗРАСТНОЙ КОЭФФИЦИЕНТ СМЕРТНОСТИ

КОЭФФИЦИЕНТ СУММАРНОЙ РОЖДАЕМОСТИ
(КСР), Total fertility rate (TFR) – не зависит от
возрастной структуры
TFR
49
n
f
nx
x 15

28. КОЭФФИЦИЕНТ СУММАРНОЙ РОЖДАЕМОСТИ (КСР), Total fertility rate (TFR) – не зависит от возрастной структуры

Численность населения
(демографической совокупности под риском
события)
на начало возрастного интервала –
знаменатель любой
демографической вероятности

29. Численность населения (демографической совокупности под риском события) на начало возрастного интервала – знаменатель любой

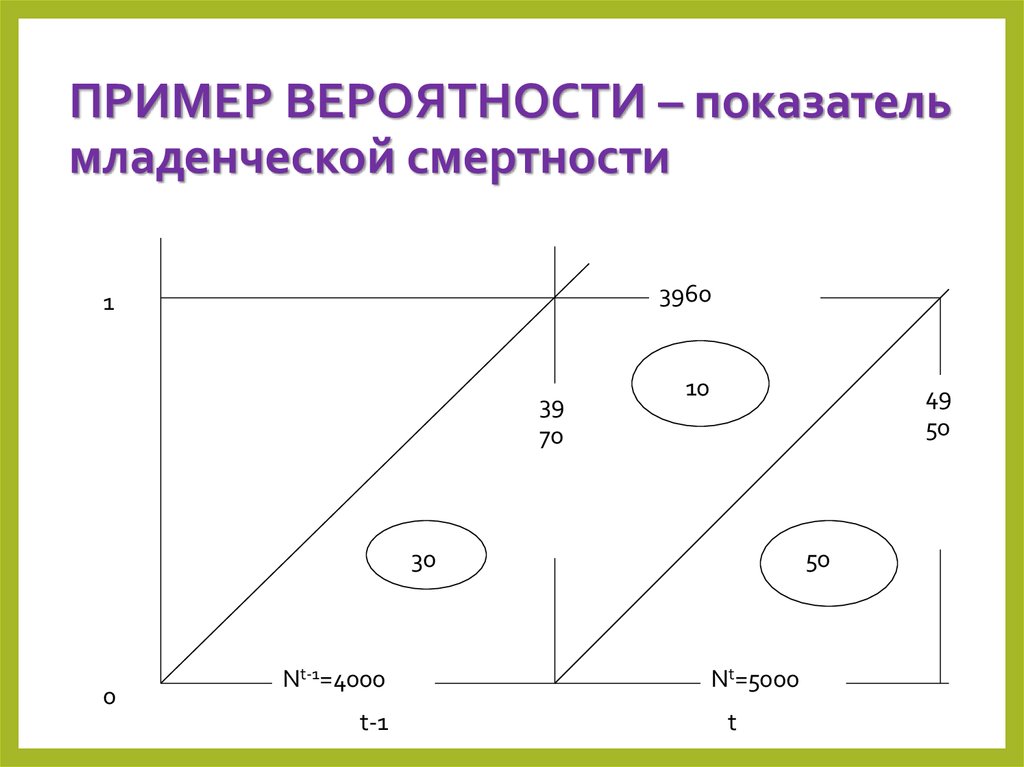
ПРИМЕР ВЕРОЯТНОСТИ – показатель
младенческой смертности
3960
1
39
70
10
49
50
30
0
Nt-1=4000
t-1
50
Nt=5000
t

30. ПРИМЕР ВЕРОЯТНОСТИ – показатель младенческой смертности

Показатель младенческой
смертности – самый грубый
t
0
t
M
m
*1000
N
0
0
10 50
m
*1000 12
5000
0
0

31. Показатель младенческой смертности – самый грубый

Показатель младенческой смертности,
рассчитанный по формуле Ратса
(с применением эмпирически найденных весовых коэффициентов,
отражающих нелинейность функции распредления риска смерти на
интервале первого года жизни новорожденного)
t
0
M
m
t 1
t
k' N k'' N
0
0

32. Показатель младенческой смертности, рассчитанный по формуле Ратса (с применением эмпирически найденных весовых коэффициентов,

Соотнесение весов формулы Ратса с
уровнем младенческой смертности
Уровень
младенческой
смертности, m0 (‰)
к’
к’’
200
60
40
150
67
33
100
75
25
50
80
20
25
85
15
15
95
5
Веса (%)

33. Соотнесение весов формулы Ратса с уровнем младенческой смертности

ПОКАЗАТЕЛЬ МЛАДЕНЧЕСКОЙ
СМЕРТНОСТИ,
рассчитанный по методу РОССТАТа
t /t
0
t
M
m (
N
t
0
t / t 1
0
t 1
M
N
) 1000

34. ПОКАЗАТЕЛЬ МЛАДЕНЧЕСКОЙ СМЕРТНОСТИ, рассчитанный по методу РОССТАТа

• Коэффициент
младенческой
смертности в году t:
m0
10 50
1
(3970 4950)
2
*1000
m0 12,87
• Вероятность
умереть
в возрасте до 1 года в
году t:
50
10
m (
) 1000
5000 4000
0
0
m 12,5
0
0

35.

КАЛЕНДАРЬ ДЕМОГРАФИЧЕСКОГО ПРОЦЕССА
Расчет среднего возраста матери при рождении
ребенка:
49
x
n
( x ) nf x
2
15
49
f
n
15
x

36. КАЛЕНДАРЬ ДЕМОГРАФИЧЕСКОГО ПРОЦЕССА Расчет среднего возраста матери при рождении ребенка:

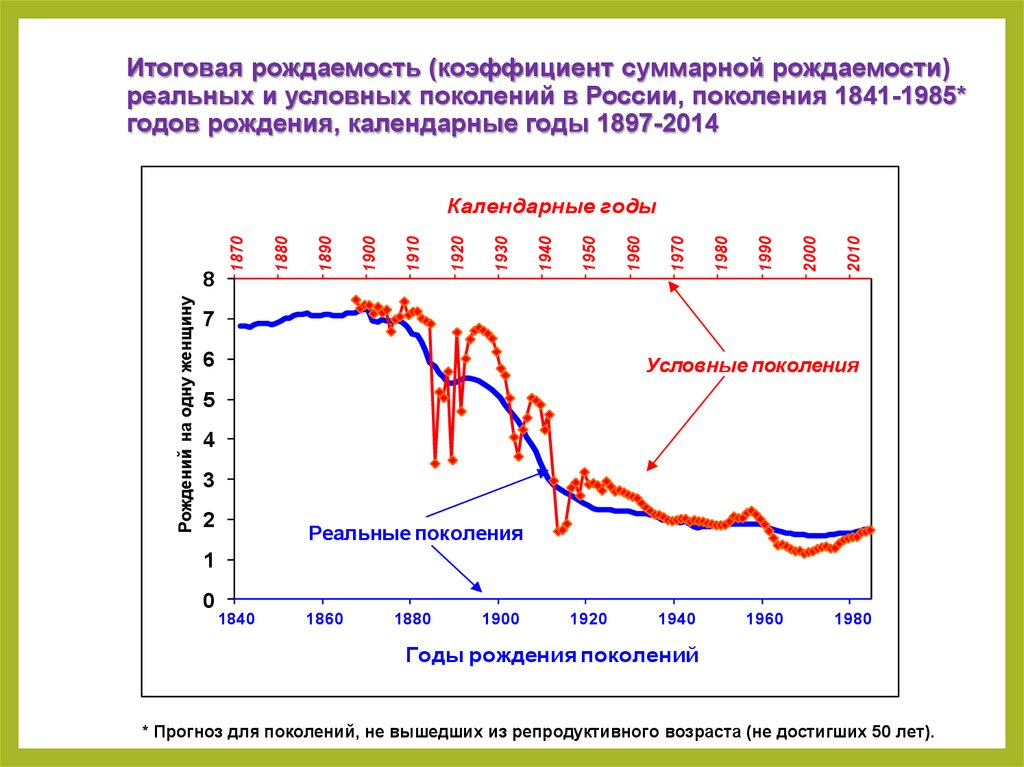
Итоговая рождаемость (коэффициент суммарной рождаемости)
реальных и условных поколений в России, поколения 1841-1985*
годов рождения, календарные годы 1897-2014
Рождений на одну женщину
2010
2000
1990
1980
1970
1960
1950
1940
1930
1920
1910
1900
1890
1880
8
1870
Календарные годы
7
6
Условные поколения
5
4
3
2
Реальные поколения
1
0
1840
1860
1880
1900
1920
1940
1960
1980
Годы рождения поколений
* Прогноз для поколений, не вышедших из репродуктивного возраста (не достигших 50 лет).

37. Итоговая рождаемость (коэффициент суммарной рождаемости) реальных и условных поколений в России, поколения 1841-1985* годов

СТАНДАРТИЗАЦИЯ
общих коэффициентов
устранение влияния
возрастной структуры
(в общем виде - состава демографической
совокупности: возрастного, брачного, по
длительности проживания и пр.)

38. СТАНДАРТИЗАЦИЯ общих коэффициентов - устранение влияния возрастной структуры (в общем виде - состава демографической

ПРЯМАЯ СТАНДАРТИЗАЦИЯ
Дано: Сравнить общие коэффициенты смертности mA и mB
Два населения
Возрастные
структуры
Распределение
умерших по
возрасту
Можно
рассчитать
возрастные
коэффициенты
смертности
А
S
В
A
x
М
S
М
A
x
М
m
S
A
x
В
x
A
x
A
x
В
x
В
x
В
x
М
m
S
В
x

39. ПРЯМАЯ СТАНДАРТИЗАЦИЯ

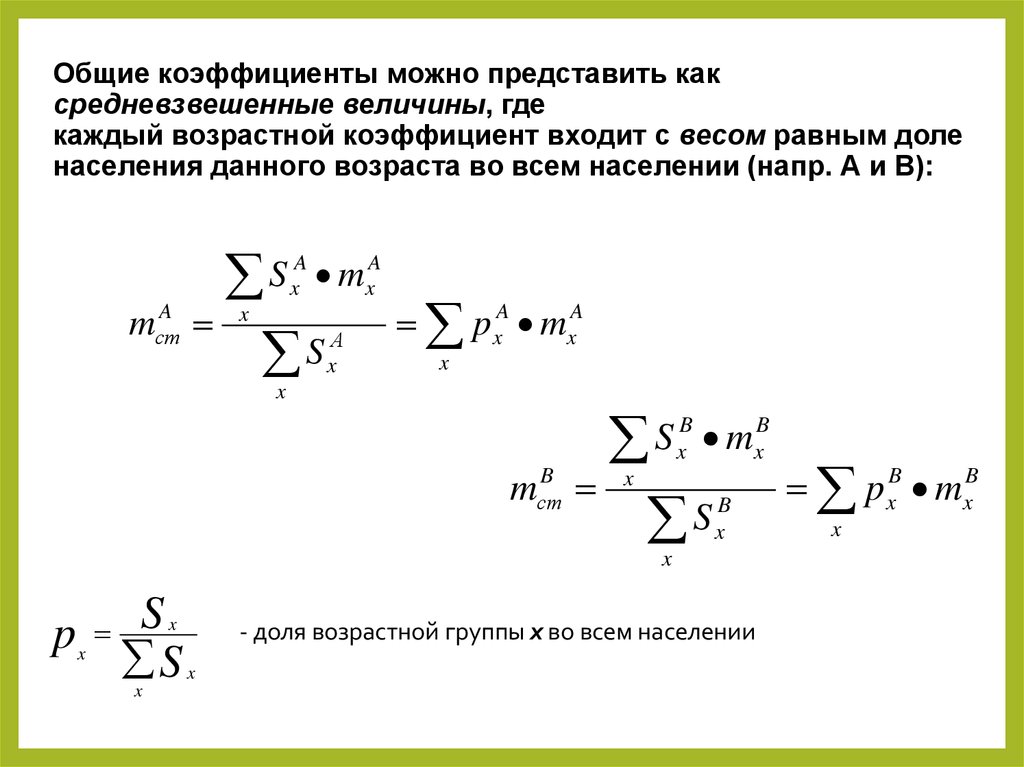
Общие коэффициенты можно представить как
средневзвешенные величины, где
каждый возрастной коэффициент входит с весом равным доле
населения данного возраста во всем населении (напр. А и В):
A
mст
A
A
S
m
x x
x
А
S
x
p xA mxA
x
x
B
mст
B
B
S
m
x x
x
B
S
x
x
p
x
S
S
x
x
- доля возрастной группы x во всем населении
x
p xB mxB
x

40. Общие коэффициенты можно представить как средневзвешенные величины, где каждый возрастной коэффициент входит с весом равным

Прямая стандартизация
станд
Выбираем население – стандарт.
x
Его возрастную структуру будем считать одинаковой и в
населении А, и в населении В и рассчитаем
стандартизованные общие коэффициенты:
S
Для А:
A
mст
станд
A
S
m
x
x
x
станд
S
x
x
Для В:
В
mст
станд
В
S
m
x
x
x
станд
S
x
x

41. Прямая стандартизация

При прямом методе стандартизации фактические
среднегодовые численности населения в этом равенстве
заменяют на некоторые стандартные (их называют весами
для стандартизации) и подсчитывают, сколько бы человек
умерло, если бы возрастной состав населения, был таким
же, как в населении, принятом за стандарт.
Разделив условное число умерших для каждого из
сравниваемых населений на численность населения,
принятого за стандарт, мы получим стандартизованные
прямым способом общие коэффициенты смертности.
В них устранены различия в возрастном составе
населения и поэтому они более правильно отражают
соотношение уровней смертности при пространственных и
временных сопоставлениях.

42. При прямом методе стандартизации фактические среднегодовые численности населения в этом равенстве заменяют на некоторые

Стандартизованные общие коэффициенты:
• Не
зависят от влияния возрастной структуры, то есть
отражают только влияние возрастной (смертности)
• Их
величина зависит от выбранного стандарта, поэтому
можно сравнивать только те коэффициенты, которые
рассчитаны при одинаковом стандарте
• Стандартизованные
коэффициенты сравниваются
словами «больше» - «меньше»

43. Стандартизованные общие коэффициенты:

Пример: Классическая задача применения
метода стандартизации коэффициентов
Данные: Петроград, 1923
Возрастные
группы
Дворники
Число
живущих
Число
умерших
Милиционеры
Число
живущих
Число
умерших
20-29
2277
19
2158
28
30-39
2541
28
1237
22
40-49
3014
69
442
9
50-59
3118
78
106
3
Всего
10950
194
3943
62

44. Пример: Классическая задача применения метода стандартизации коэффициентов Данные: Петроград, 1923

Смертность выше среди дворников или милиционеров?
Решение: Шаг 1 (расчет коэффициентов и структур, выбор
метода – прямая стандартизация)
Возрастные
группы
Дворники
Милиционеры
Возрастной
состав, %
Возрастные
коэф.-ты,
на 1000
Возрастной
состав, %
Возрастные
коэф.-ты,
на 1000
20-29
20,8
8,34
54,7
12,97
30-39
23,2
11,02
31,4
17,78
40-49
27,5
22,89
11,2
20,36
50-59
28,5
25,02
2,7
28,30
Всего
100,0
17,72
100,0
15,72

45. Смертность выше среди дворников или милиционеров? Решение: Шаг 1 (расчет коэффициентов и структур, выбор метода – прямая

Смертность выше среди дворников или
милиционеров?
Решение: Шаг 2 (Выбор стандартного «населения»)
Возрастной состав Возрастной состав
населения
совокупности
Петрограда, 1923,% «дворники+милиционеры»,%
20-29
39,2
29,8
30-39
29,2
25,4
40-49
20,4
23,2
50-59
11,2
21,6
Всего
100,0
100,0

46. Смертность выше среди дворников или милиционеров? Решение: Шаг 2 (Выбор стандартного «населения»)

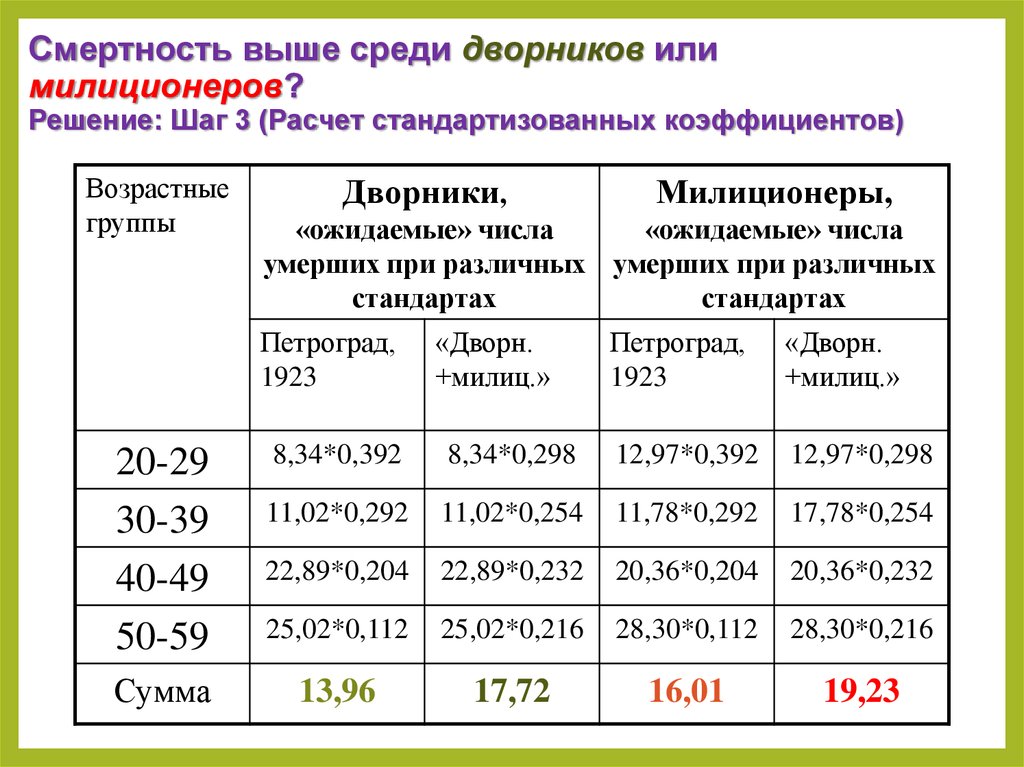
Смертность выше среди дворников или
милиционеров?
Решение: Шаг 3 (Расчет стандартизованных коэффициентов)
Возрастные
группы
Дворники,
«ожидаемые» числа
«ожидаемые» числа
умерших при различных умерших при различных
стандартах
стандартах
Петроград,
1923
20-29
30-39
40-49
50-59
Сумма
Милиционеры,
«Дворн.
+милиц.»
Петроград,
1923
«Дворн.
+милиц.»
8,34*0,392
8,34*0,298
12,97*0,392
12,97*0,298
11,02*0,292
11,02*0,254
11,78*0,292
17,78*0,254
22,89*0,204
22,89*0,232
20,36*0,204
20,36*0,232
25,02*0,112
25,02*0,216
28,30*0,112
28,30*0,216
13,96
17,72
16,01
19,23

47. Смертность выше среди дворников или милиционеров? Решение: Шаг 3 (Расчет стандартизованных коэффициентов)

Смертность выше среди дворников или
милиционеров?
Решение: Шаг 4 (Сравнение результатов и выводы)
Дворники
Общий коэффициент
смертности (факт)
17,72
Милиционеры Милиц.
/Дворн.
15,72
0,89
Стандартизованные коэффициенты при различном стандарте
возрастного состава
Стандарт – Население
Петрограда, 1923
13,96
17,60
1,26
Стандарт –
«дворники+милиционеры»
16,01
19,23
1,20

48. Смертность выше среди дворников или милиционеров? Решение: Шаг 4 (Сравнение результатов и выводы)

Пример европейского и мирового стандартов, которые
используют в межстрановых сравнениях общих коэффициентов, в
особенности смертности от отдельных причин смерти
Возраст
(лет)
Eвропейский
стандарт
Mировой
стандарт
Возраст
(лет)
Eвропейский
стандарт
Mировой
стандарт
0
0.016
0.024
45-49
0.070
0.060
1-4
0.064
0.096
50-54
0.070
0.050
5-9
0.070
0.100
55-59
0.060
0.040
10-14
0.070
0.090
60-64
0.050
0.040
15-19
0.070
0.090
65-69
0.040
0.030
20-24
0.070
0.080
70-74
0.030
0.020
25-29
0.070
0.080
75-79
0.020
0.010
30-34
0.070
0.060
80-84
0.010
0.005
35-39
0.070
0.060
85+
0.010
0.005
40-44
0.070
0.060

49. Пример европейского и мирового стандартов, которые используют в межстрановых сравнениях общих коэффициентов, в особенности

КОСВЕННАЯ СТАНДАРТИЗАЦИЯ
Дано: Сравнить общие коэффициенты смертности mA и mB
Два населения
Возрастные
структуры
Общие числа
умерших
Нельзя
рассчитать
возрастные
коэффициенты
смертности
А
S
A
x
М
?
В
S
A
В
x
М
?
В

50. КОСВЕННАЯ СТАНДАРТИЗАЦИЯ

Косвенная стандартизация
станд
x
m
Выбираем население – стандарт.
Рассчитаем отношение реального количества
смертей к «ожидаемому», которое могло бы
быть при реальной возрастной структуре и
возрастных коэффициентах смертности
стандарта, и умножим его на общий
коэффициент смертности стандарта :
A
mст
МА
станд
m
А
станд
S
m
x x
x
В
mст
МВ
станд
m
В
станд
S
m
x x
x

51. Косвенная стандартизация

При косвенном методе стандартизации объектом замены служат
возрастные коэффициенты смертности.
Подсчитывается, сколько бы человек умерло, если бы возрастные
коэффициенты смертности, были такими, как в населении, принятом за
стандарт.
В качестве стандарта принимается обычно некоторое третье население,
для которого имеются данные о возрастном составе и возрастные
коэффициенты смертности.
При сравнении коэффициентов по регионам страны стандартом может
служить население всей страны или одного из сравниваемых регионов.
Разделив фактическое общее число умерших для каждого из
сравниваемых населений на условное, получим индекс смертности,
показывающий соотношение чисел смертей в фактическом населении и в
населении, принятом за стандарт, при одинаковой, на этот раз
фактической, возрастной структуре.
А умножив этот индекс на общий коэффициент смертности населения,
принятого за стандарт, получим коэффициент смертности,
стандартизованный косвенным способом.
Он также не зависит от различий в возрастном составе сравниваемых
населений, однако вместе с тем учитывает особенности их возрастной
смертности.

52. При косвенном методе стандартизации объектом замены служат возрастные коэффициенты смертности. Подсчитывается, сколько бы

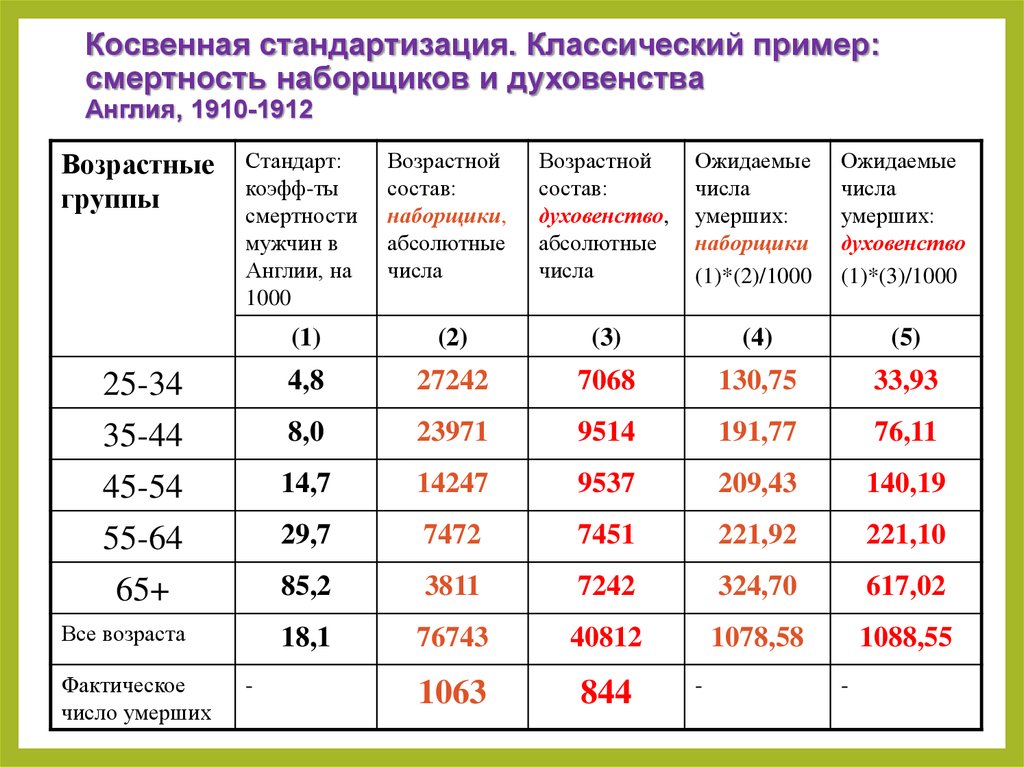
Косвенная стандартизация. Классический пример:
смертность наборщиков и духовенства
Англия, 1910-1912
Стандарт:
коэфф-ты
смертности
мужчин в
Англии, на
1000
Возрастной
состав:
наборщики,
абсолютные
числа
Возрастной
состав:
духовенство,
абсолютные
числа
Ожидаемые
числа
умерших:
наборщики
(1)*(2)/1000
Ожидаемые
числа
умерших:
духовенство
(1)*(3)/1000
(1)
(2)
(3)
(4)
(5)
25-34
4,8
27242
7068
130,75
33,93
35-44
45-54
55-64
8,0
23971
9514
191,77
76,11
14,7
14247
9537
209,43
140,19
29,7
7472
7451
221,92
221,10
65+
85,2
3811
7242
324,70
617,02
18,1
76743
40812
1078,58
1088,55
1063
844
Возрастные
группы
Все возраста
Фактическое
число умерших
-
-
-

53. Косвенная стандартизация. Классический пример: смертность наборщиков и духовенства Англия, 1910-1912

Выше смертность среди наборщиков
или среди духовенства?
Стандартизованные
коэффициенты
Наборщики
Духовенство
(1063/1079)*18,1
= 17,8
(844/1089)*18,1
= 14,0

54. Выше смертность среди наборщиков или среди духовенства?

Методика получения
стандартизованных специальных
коэффициентов рождаемости
не отличается от описанной ранее.
Однако они рассчитываются только
для женщин 15-49 лет.

55. Методика получения стандартизованных специальных коэффициентов рождаемости не отличается от описанной ранее. Однако они

Стандартизованные коэффициенты
независимо от способа получения
(прямой, косвенный метод) пригодны
только для сравнений. Это
абстрактные математические
величины и самостоятельного
значения не имеют.
Сравнения стандартизованных
коэффициентов можно проводить только в тех
случаях, когда они исчислены с применением
одного и того же стандарта.
• Желательно, чтобы выбранный стандарт
максимально возможно соответствовал
«усредненной» характеристике сравниваемых
совокупностей

56.

Использование метода стандартизации
в практике демографического анализа
Прямой метод стандартизации
• Стандартизованные
по возрасту коэффициенты
смертности по причинам смерти (международная практика
с установленным «стандартным населением»:
«европейский», «мировой» стандарты)
• Стандартизация
по возрасту и полу вероятностей
наступления событий (коэффициентов интенсивности,
распространенности) при сравнении сильно неоднородных
совокупностей (широкая практика для анализа
социологических данных).

57. Использование метода стандартизации в практике демографического анализа

Косвенный метод стандартизации
• Пространственно-временное
сравнение общих
коэффициентов демографических процессов, когда
неизвестны фактические возрастные профили процессов
(возрастные коэффициенты неизвестны или ненадежны).
Примеры: Индексы рождаемости Коула (стандарт – брачная
рождаемость секты Гуттеритов), ГМЕР Борисова (стандарт
– модельная оценка минимальных коэффициентов
рождаемости при отсутствии намеренного ограничения
рождаемости в семье).