Перпендикулярность прямой и плоскости

1.

2.

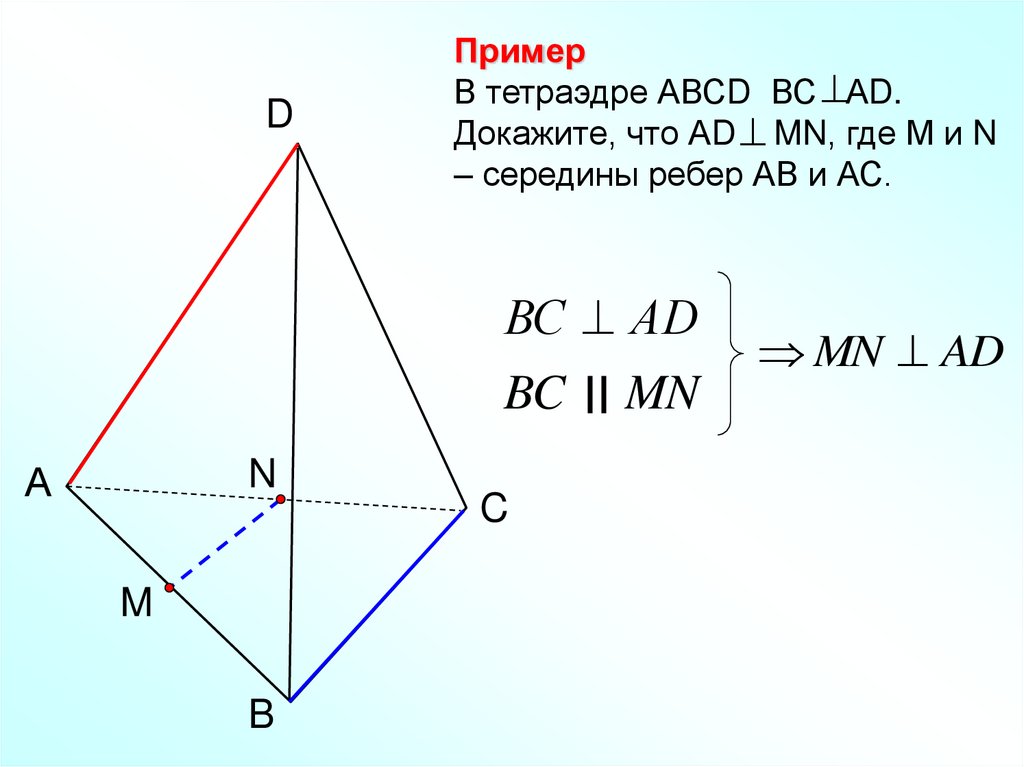
D
Пример
В тетраэдре АВСD ВС АD.
Докажите, что АD MN, где М и N
– середины ребер АВ и АС.
ВС АD
BC II MN
N
А
M
B
C
MN AD

3.

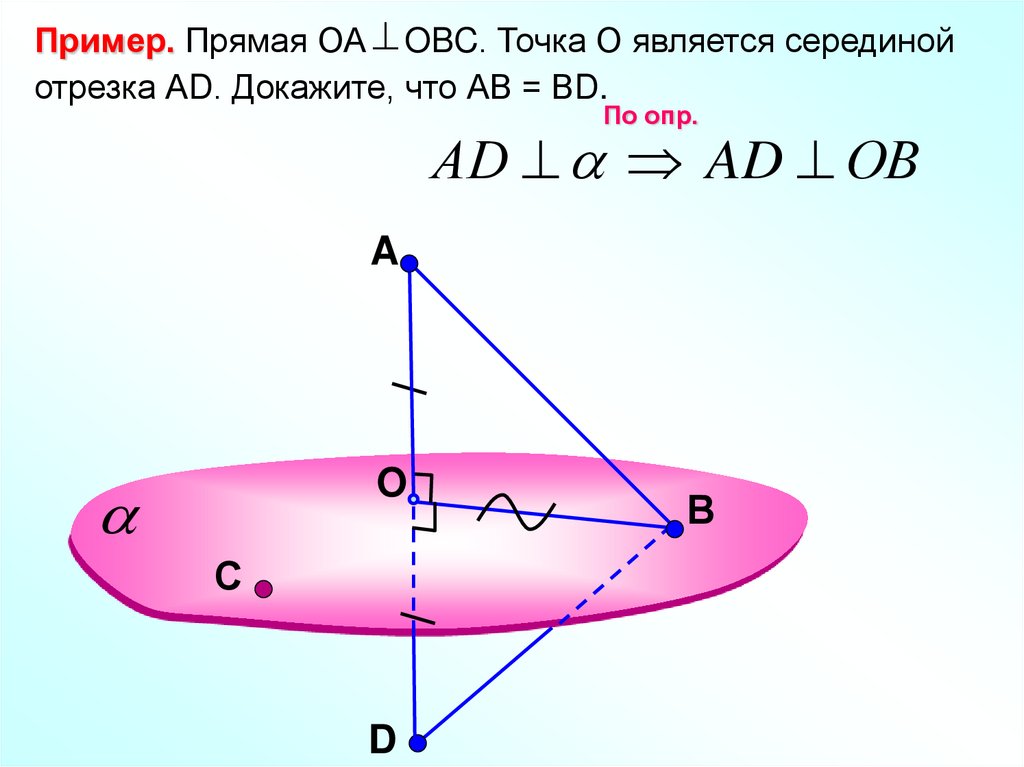
Пример. Прямая ОА OBC. Точка О является серединой
отрезка АD. Докажите, что АВ = ВD.
По опр.
АD AD ОВ
A
O
С
D
В

4.

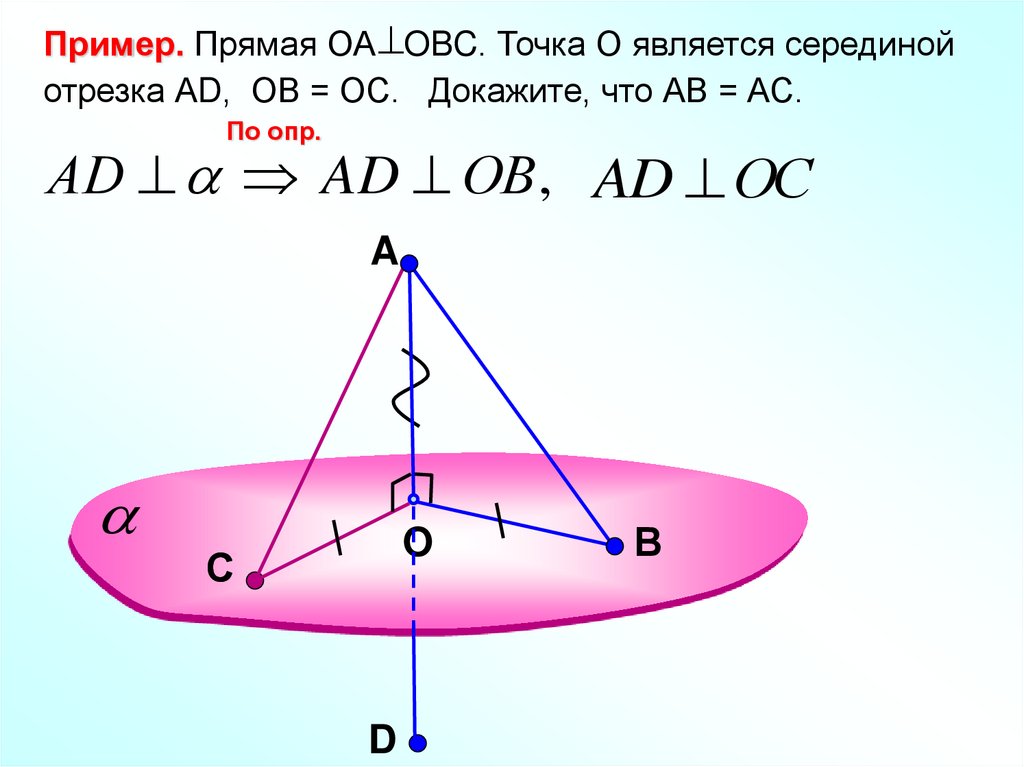
Пример. Прямая ОА OBC. Точка О является серединой
отрезка АD, ОВ = ОС. Докажите, что АВ = АС.
По опр.
АD AD ОВ , AD ОС
A
O
С
D
В

5.

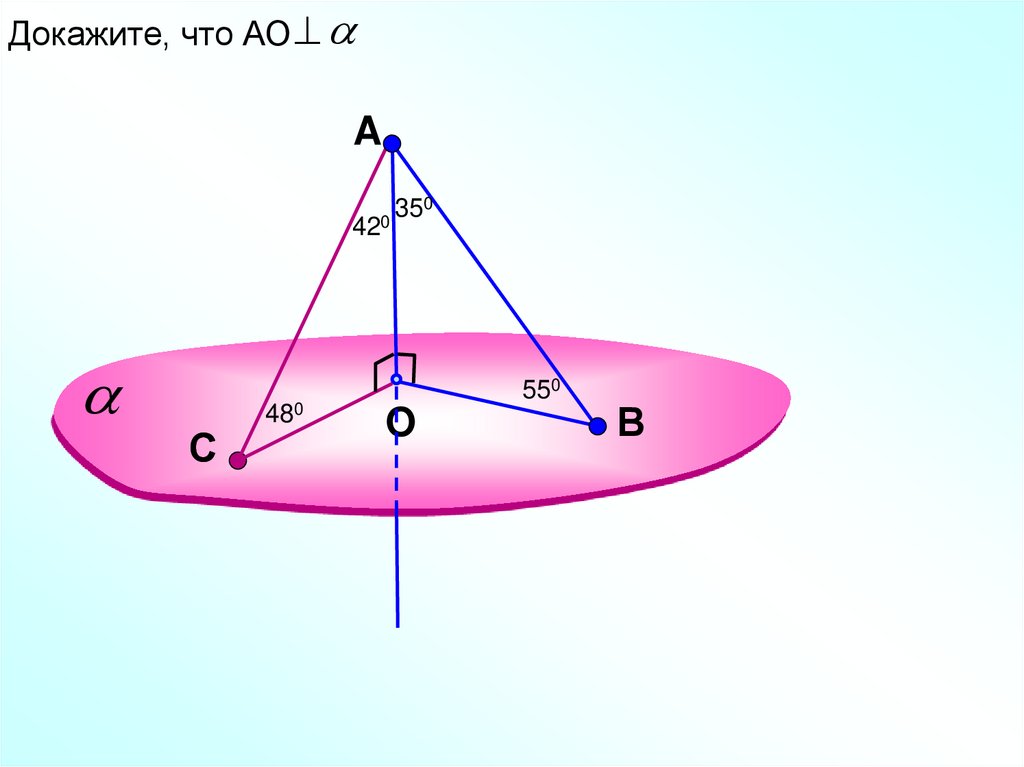
Докажите, что АО
A
0
35
420
С
480
550
O
В

6.

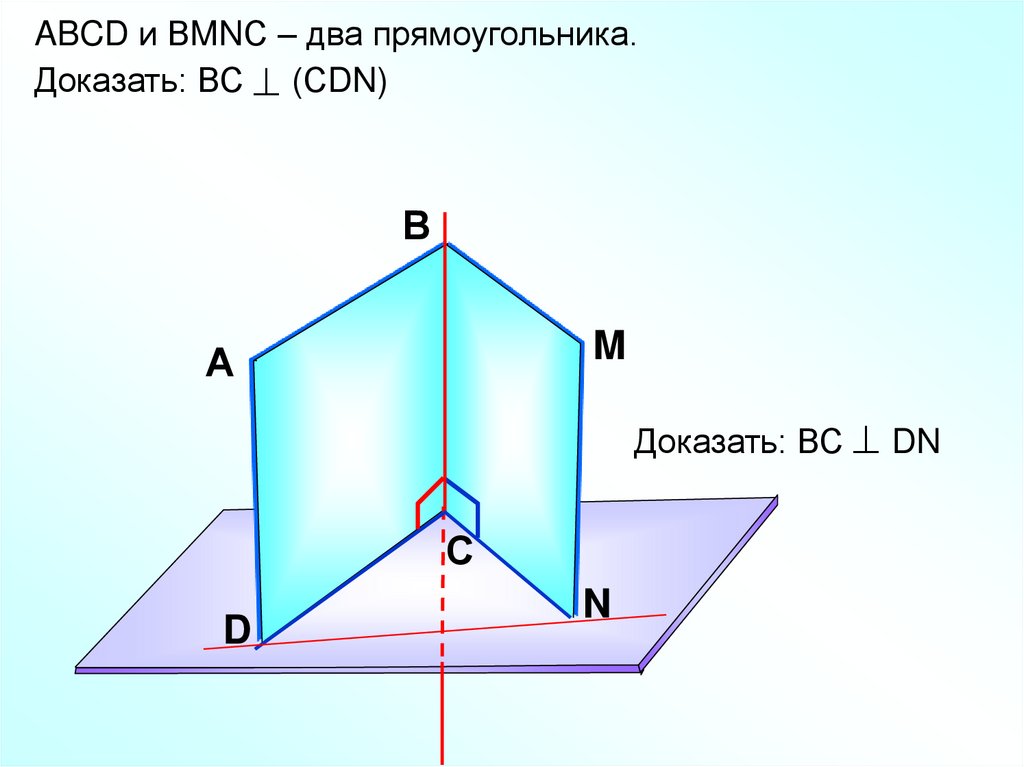
ABCD и ВMNС – два прямоугольника.
Доказать: ВС (СDN)
В
M
А
Доказать: ВС DN
С
D
N

7.

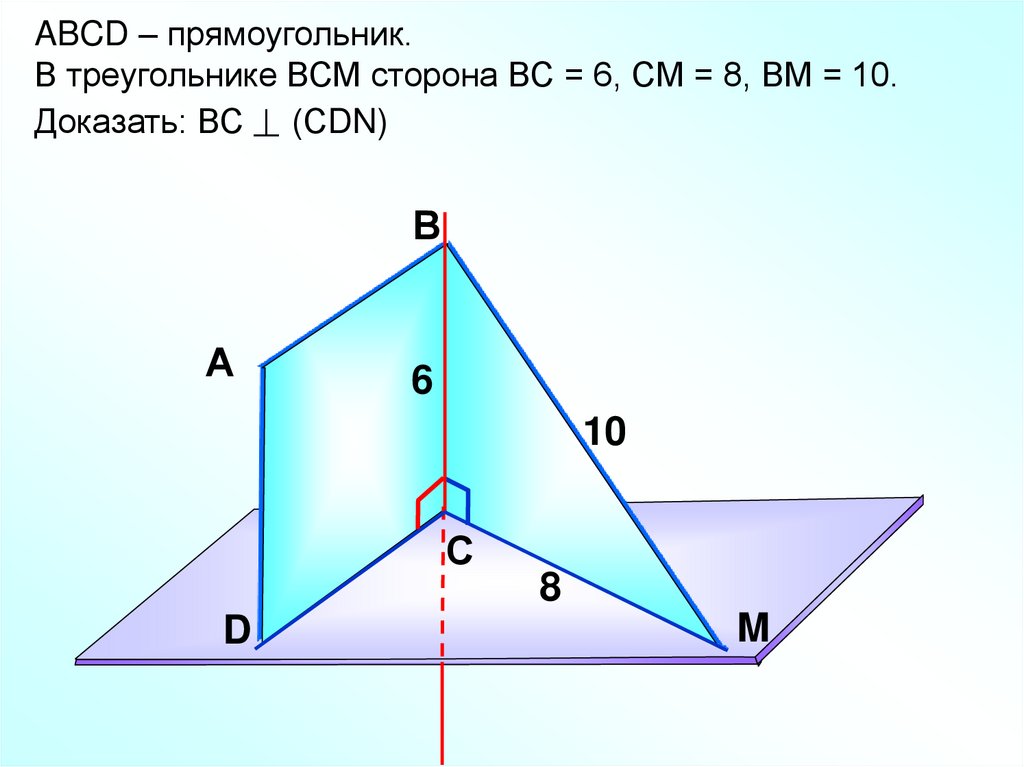
ABCD – прямоугольник.
В треугольнике ВСМ сторона ВС = 6, СМ = 8, ВМ = 10.
Доказать: ВС (СDN)
В
А
6
10
С
D
8
M

8.

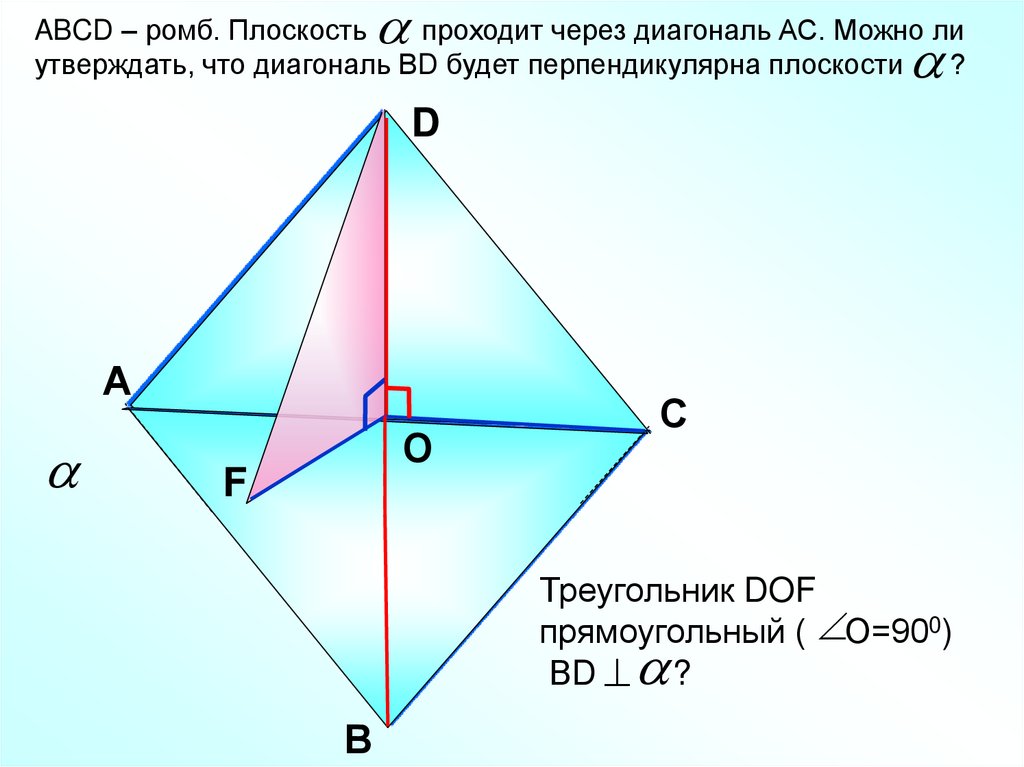
ABCD – ромб. Плоскость
проходит через диагональ АС. Можно ли
утверждать, что диагональ ВD будет перпендикулярна плоскости
?
D
А
О
F
С
Треугольник DOF
прямоугольный ( О=900)
ВD ?
В

9.

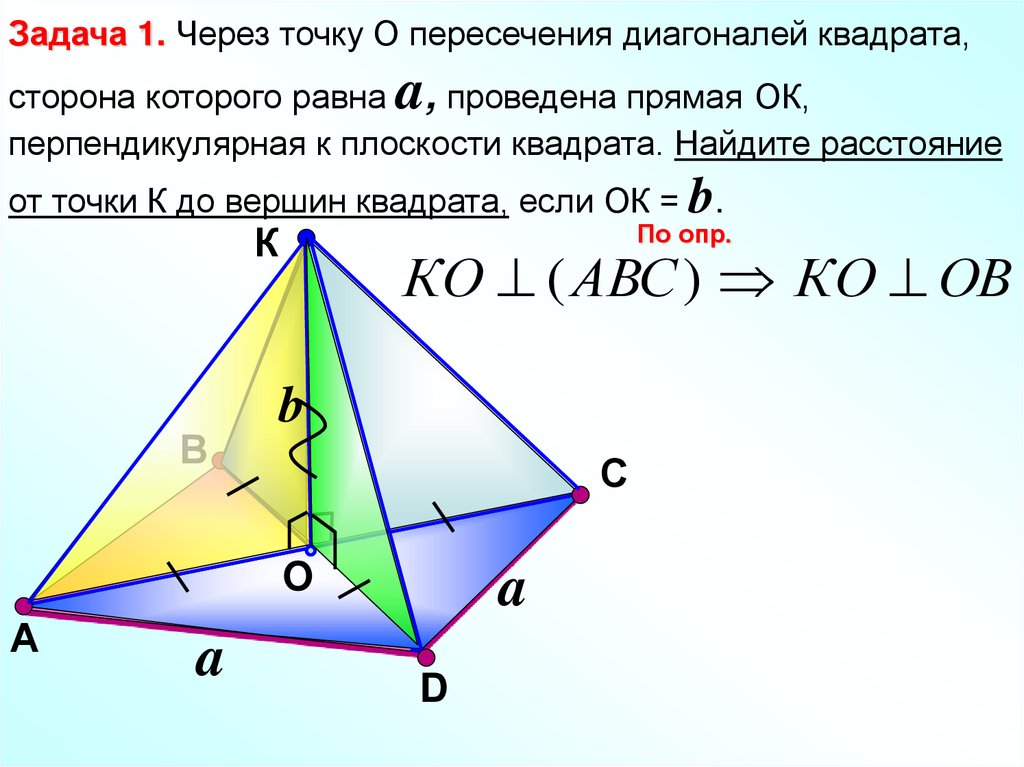
Задача 1. Через точку О пересечения диагоналей квадрата,
a
сторона которого равна , проведена прямая ОК,
перпендикулярная к плоскости квадрата. Найдите расстояние
от точки К до вершин квадрата, если ОК = b.
По опр.
К
В
КО ( АВС ) КО ОВ
b
С
O
А
a
a
D

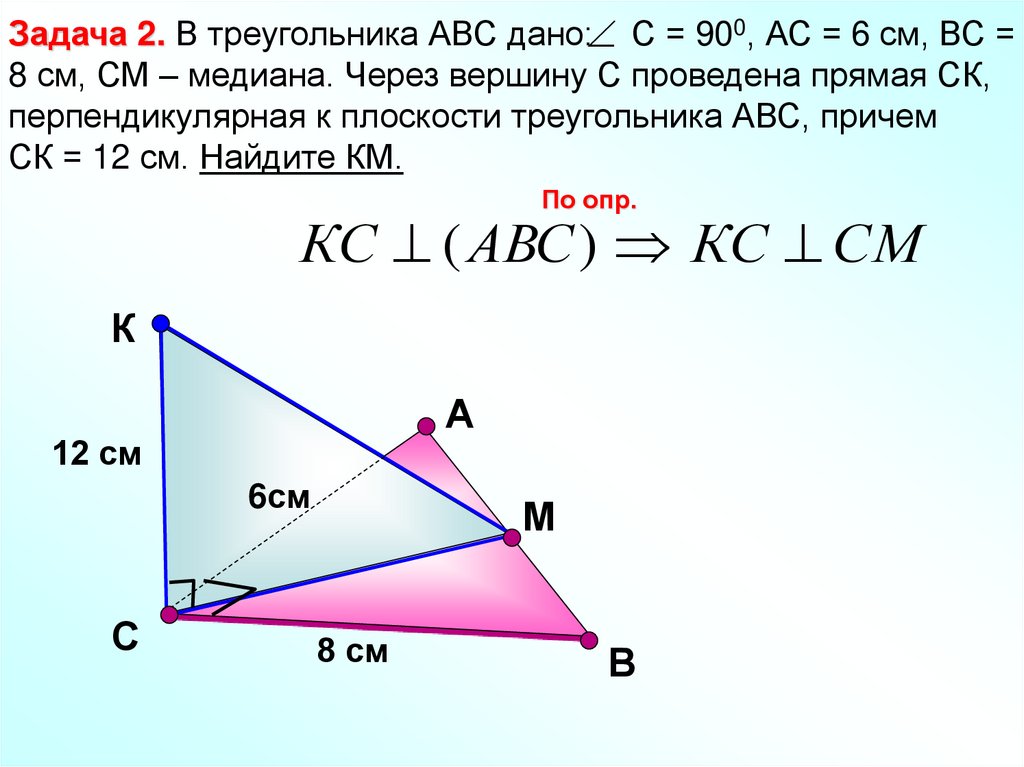
10.

Задача 2. В треугольника АВС дано: С = 900, АС = 6 см, ВС =
8 см, СМ – медиана. Через вершину С проведена прямая СК,
перпендикулярная к плоскости треугольника АВС, причем
СК = 12 см. Найдите КМ.
По опр.
КС ( АВС ) КС СМ
К
А
12 см
6см
С
М
8 см
В

11.

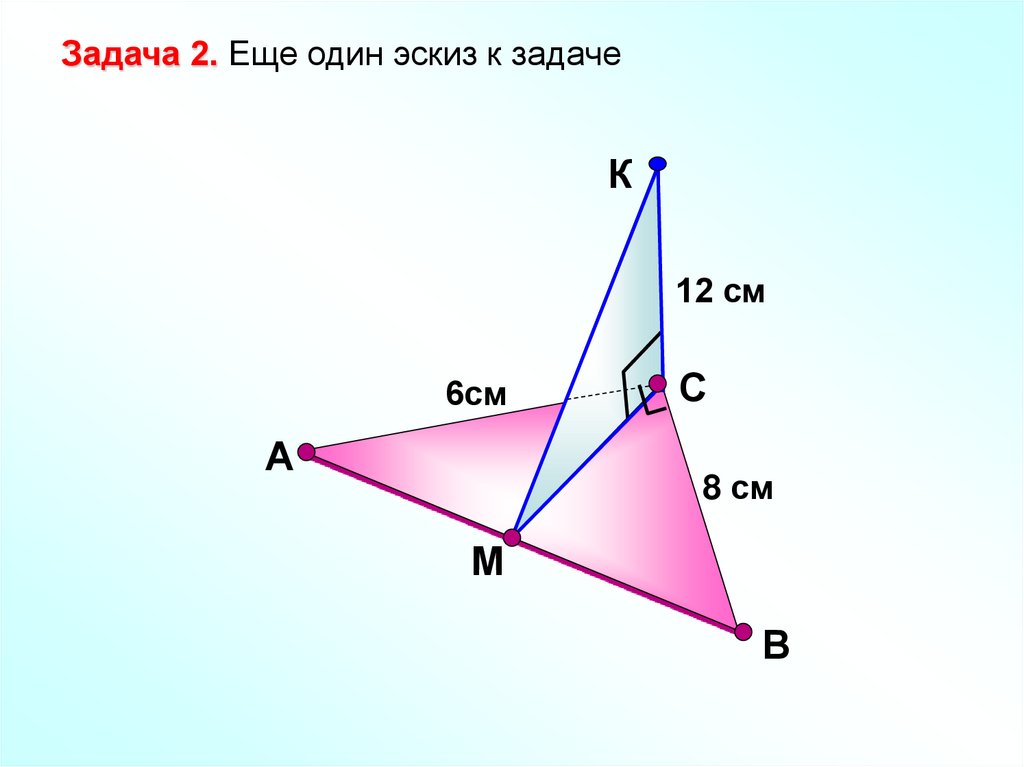
Задача 2. Еще один эскиз к задаче
К
12 см
6см
А
С
8 см
М
В

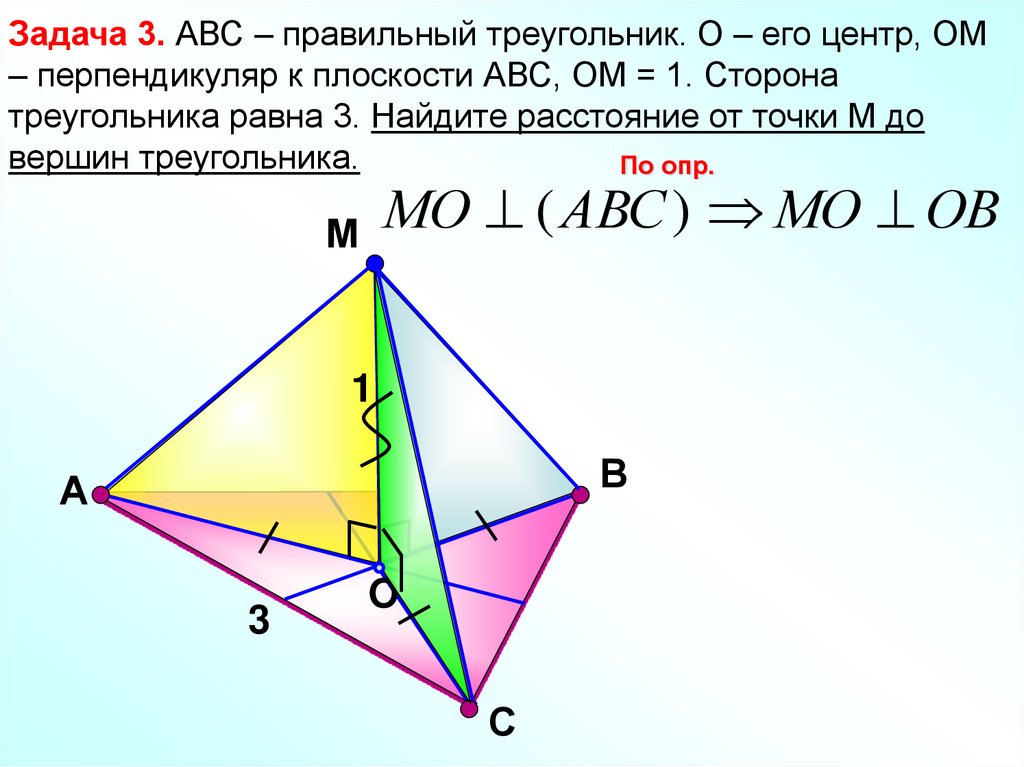
12.

Задача 3. АВС – правильный треугольник. О – его центр, ОМ
– перпендикуляр к плоскости АВС, ОМ = 1. Сторона
треугольника равна 3. Найдите расстояние от точки М до
вершин треугольника.
По опр.
МО ( АВС ) МО ОВ
М
1
В
А
3
O
С

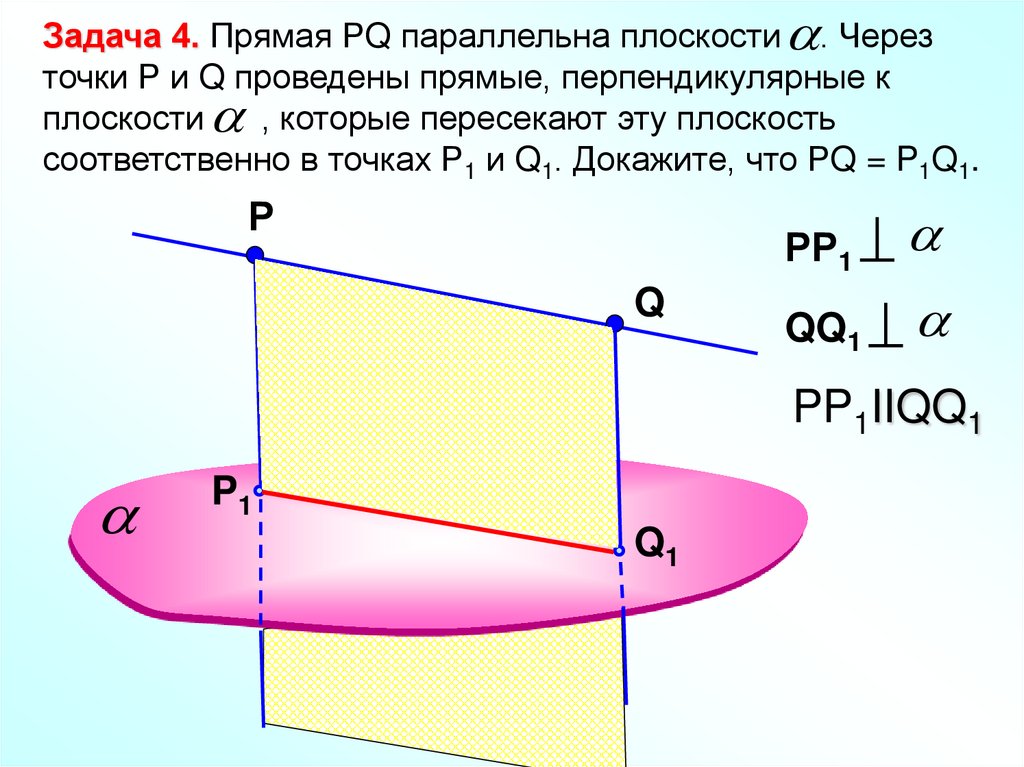
13.

Задача 4. Прямая РQ параллельна плоскости . Через
точки Р и Q проведены прямые, перпендикулярные к
плоскости , которые пересекают эту плоскость
соответственно в точках Р1 и Q1. Докажите, что РQ = P1Q1.
Р
Q
РР1
QQ1
PP1IIQQ1
P1
Q1

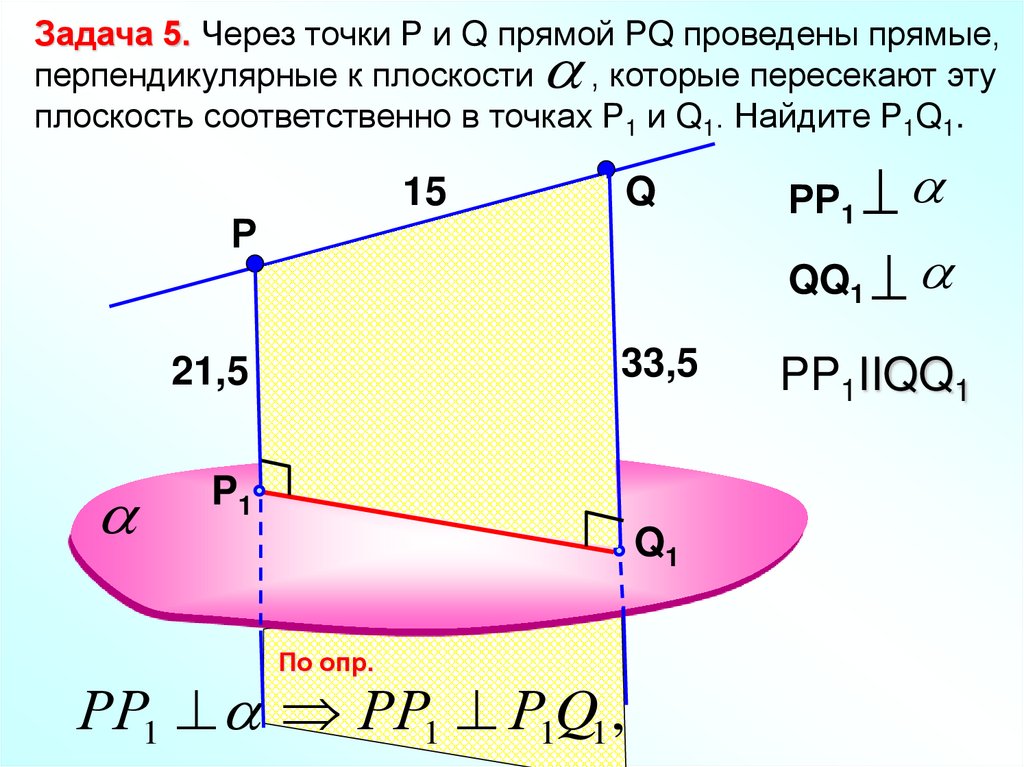
14.

Задача 5. Через точки Р и Q прямой PQ проведены прямые,
перпендикулярные к плоскости
, которые пересекают эту
плоскость соответственно в точках Р1 и Q1. Найдите Р1Q1.
15
Р
33,5
21,5
Q
P1
Q1
По опр.
РР1 РР1 Р1Q1 ,
РР1
QQ1
PP1IIQQ1

15.

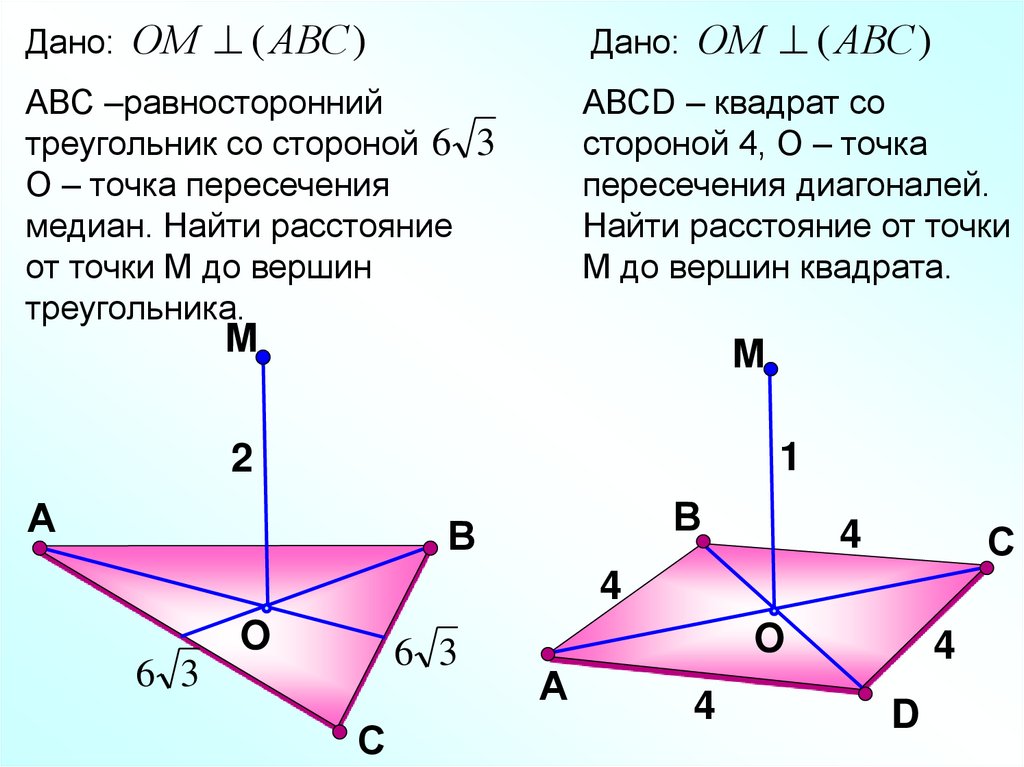
Дано:
ОМ ( АВС )
Дано:
АВС –равносторонний
треугольник со стороной 6 3
О – точка пересечения
медиан. Найти расстояние
от точки М до вершин
треугольника.
ОМ ( АВС )
АВСD – квадрат со
стороной 4, О – точка
пересечения диагоналей.
Найти расстояние от точки
М до вершин квадрата.
М
М
1
2
А
В
В
4
С
4
O
6 3
6 3
С
O
А
4
4
D

16.

D
К
Дано: ABC – р/с;
О – центр ABC
CD (ABC); ОК || CD
АB = 16 3, OK = 12; CD = 16
Найти: AD; BD; AK; BK.
16
Решение:
12
В
C
O
А