Производная на графиках

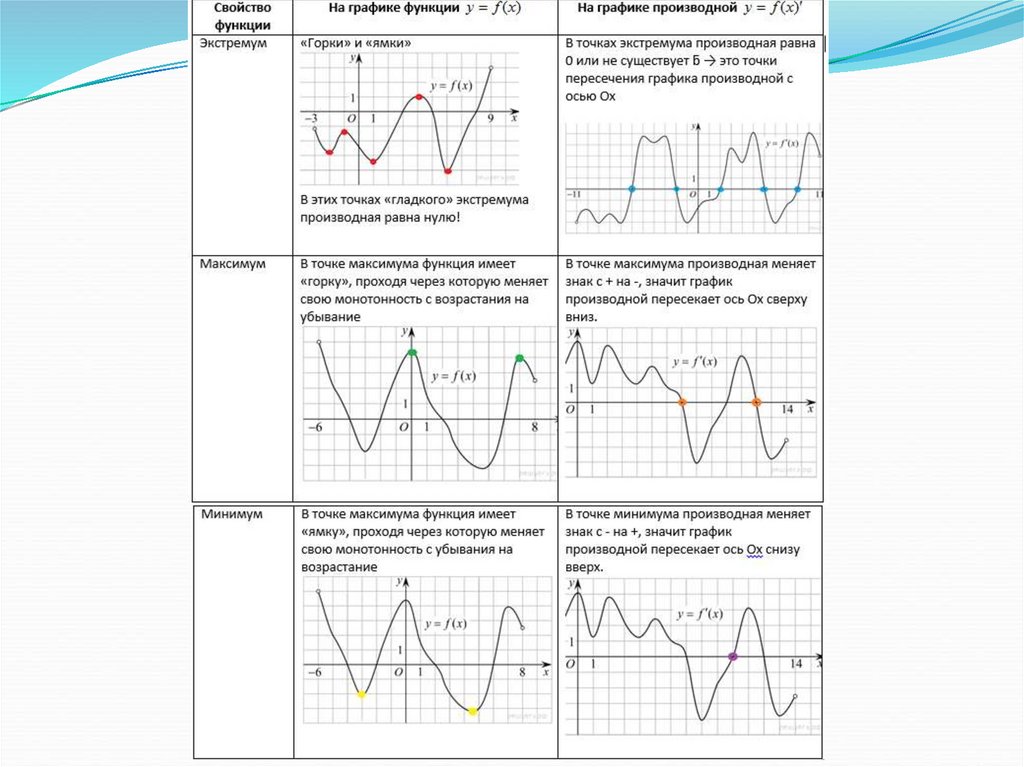
1.

2.

3.

4.

5.

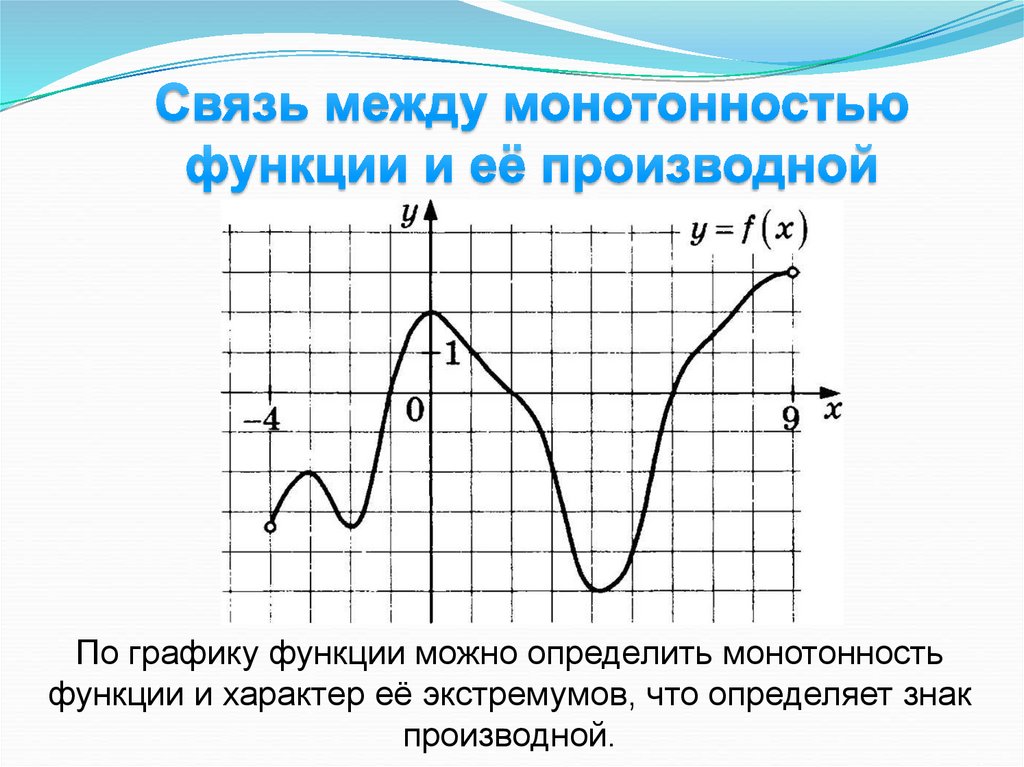
По графику функции можно определить монотонность
функции и характер её экстремумов, что определяет знак
производной.

6.

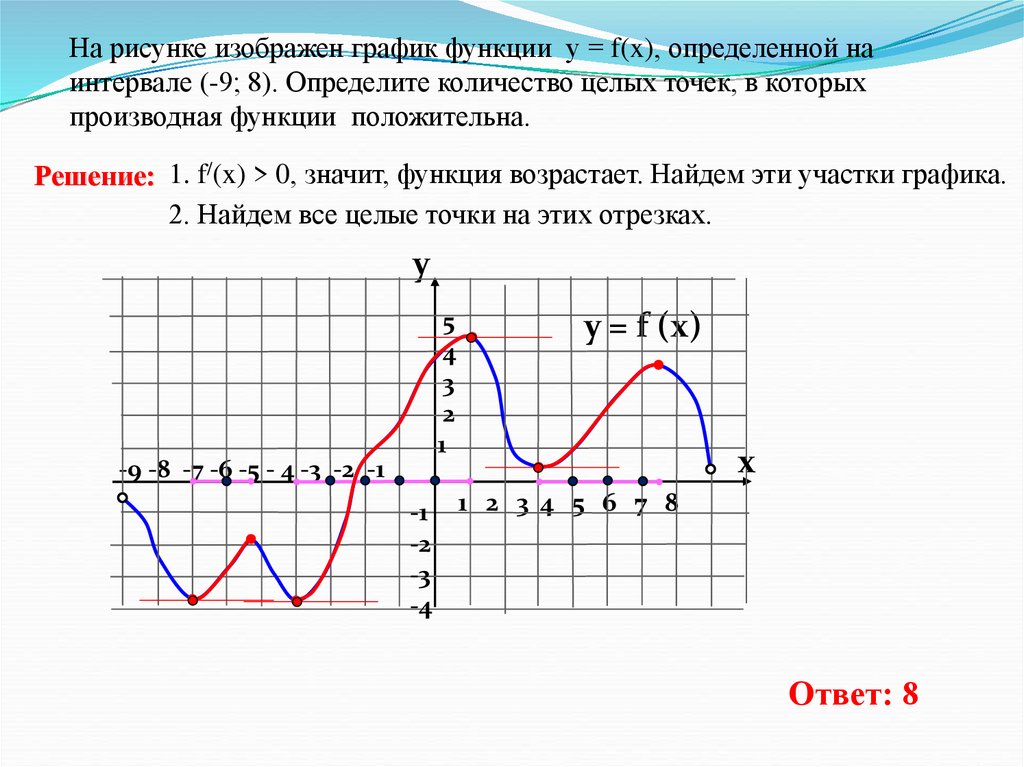
На рисунке изображен график функции у = f(x), определенной на
интервале (-9; 8). Определите количество целых точек, в которых
производная функции положительна.
Решение: 1. f/(x) > 0, значит, функция возрастает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
y
5
4
3
2
1
-9 -8 -7 -6 -5 - 4 -3 -2 -1
-1
-2
-3
-4
y = f (x)
x
1 2 3 4 5 6 7 8
Ответ: 8

7.

На рисунке изображен график функции у = f(x), определенной на
интервале (-5; 5). Определите количество целых точек, в которых
производная функции отрицательна.
Решение: 1. f/(x) < 0, значит, функция убывает. Найдем эти участки графика.
2. Найдем все целые точки на этих отрезках.
y
5
4
3
2
1
-9 -8 -7 -6 -5 - 4 -3 -2 -1
-1
-2
-3
-4
y = f (x)
x
1 2 3 4 5 6 7 8
Ответ: 5

8.

На рисунке изображен график y=f'(x) — производной функции f(x) ,
определенной на интервале (-6;8) . Найдите промежутки возрастания функции
f(x) . В ответе укажите длину наибольшего из них.
Ответ: 6

9.

На рисунке изображен график y=f'(x) — производной функции
f(x),
определенной на интервале (-8;6). Найдите промежутки убывания
функции f(x). В ответе укажите длину наибольшего из них.
Ответ: 3

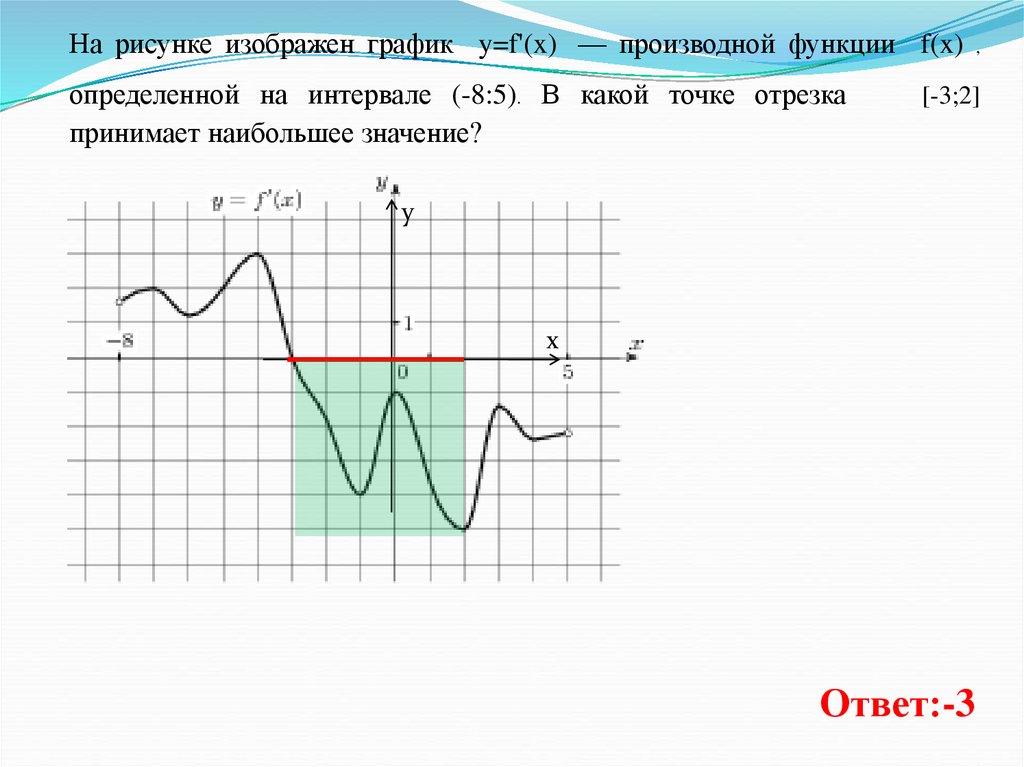
10.

На рисунке изображен график y=f'(x) — производной функции f(x)
определенной на интервале (-8:5). В какой точке отрезка
принимает наибольшее значение?
,
[-3;2]
у
х
Ответ:-3

11.

Ответ: -7

12.

По графику производной определяется знак
производной, что определяет характер
монотонности и вид экстремумов

13.

На рисунке изображен график функции
f(x), определенной на
интервале (-3;10) . Найдите сумму точек экстремума функции f(x) .
2 3
-1 0
1
6 7 8 9
-1 + 0 + 1+2 + 3 + 6 + 7+ 8 + 9= 35
Ответ: 35

14.

На рисунке изображен график y=f'(x)
— производной функции f(x) ,
определенной на интервале (-2;20) . Найдите количество точек максимума
функции f(x) , принадлежащих отрезку [-1;18] .
f ( x) 0
f ( x) 0
f/(x)
f(x)
+
–
+
–
+
_
+
x
Точка максимума – точка перехода от
графика функции к
f ( x) 0
f ( x) 0
Ответ: 3

15.

Непрерывная функция у = f(x) задана на отрезке [a;b]
На рисунке изображен ее график. В ответе укажите количество точек
графика этой функции, в которых касательная параллельна оси Ох.
y
y = f(x)
a
b
x
Ответ: 5

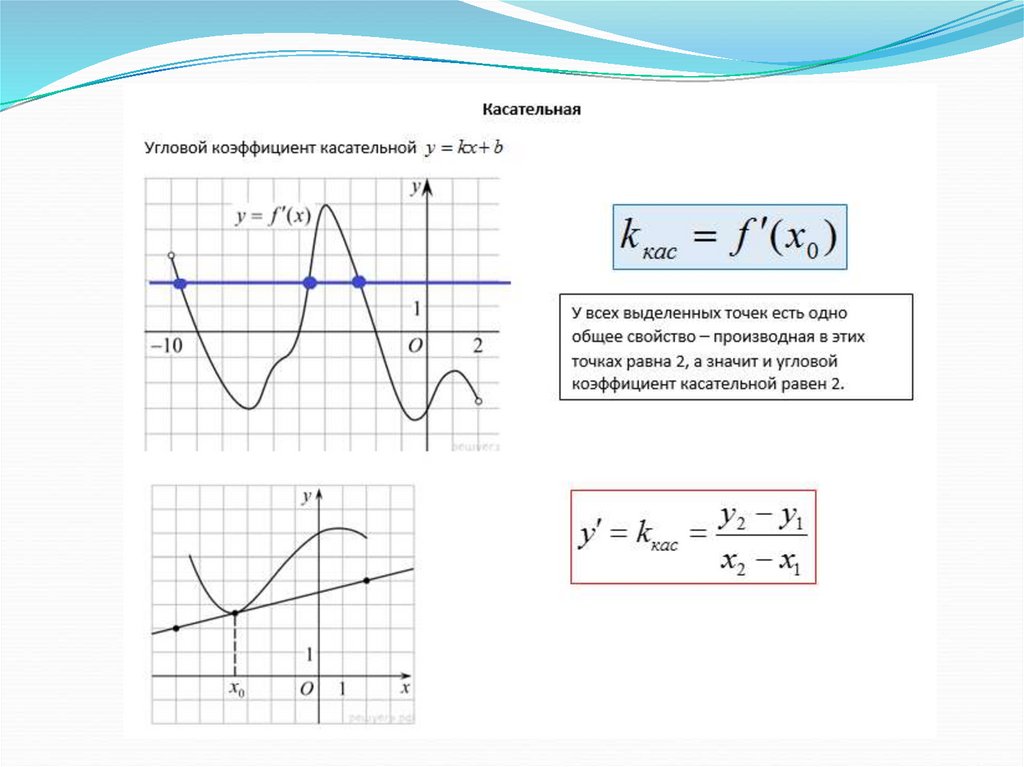
16.

На рисунке изображен график функции y = f(x), определенной на интервале
(−5; 5). Найдите количество точек, в которых касательная к графику
функции параллельна прямой y = 6 или совпадает с ней.
Ответ: 4

17.

На рисунке изображен график функции y = f(x), определенной на интервале
(−3; 9). Найдите количество точек, в которых касательная к графику функции
параллельна прямой y = 12 или совпадает с ней.
Ответ: 5

18.

На рисунке изображен график производной функции f(x), определенной
на интервале (−10; 2). Найдите количество точек, в которых касательная к
графику функции f(x) параллельна прямой y = −2x − 11 или совпадает с
ней.
Ответ: 5

19.

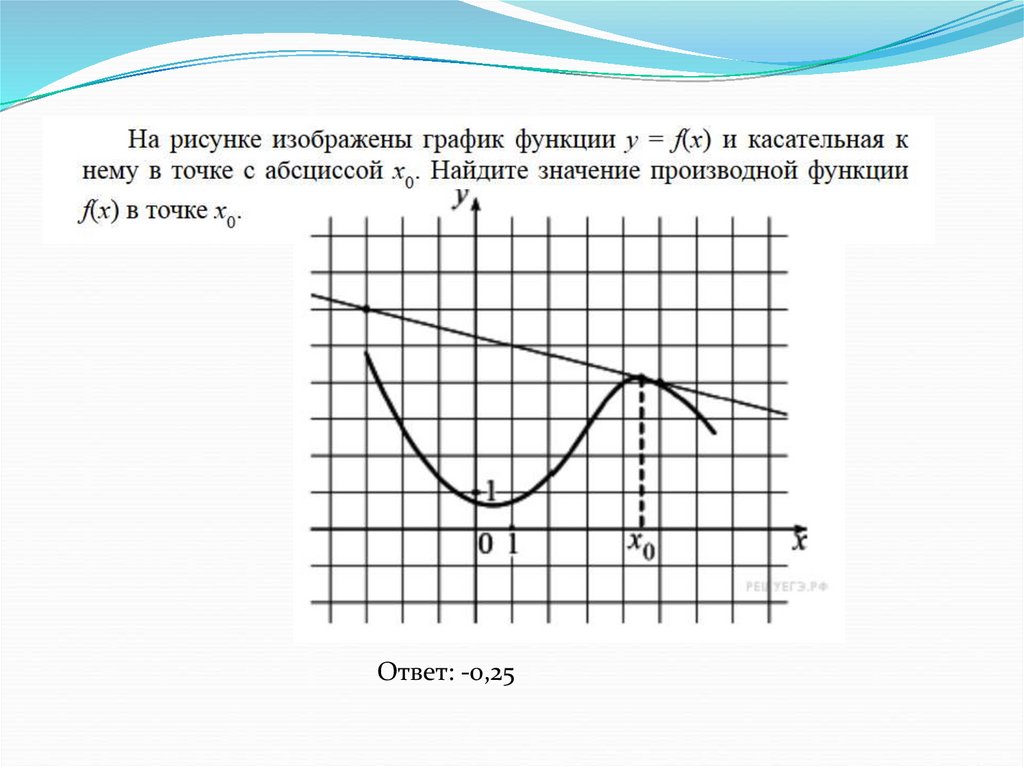
Ответ: -0,25

20.

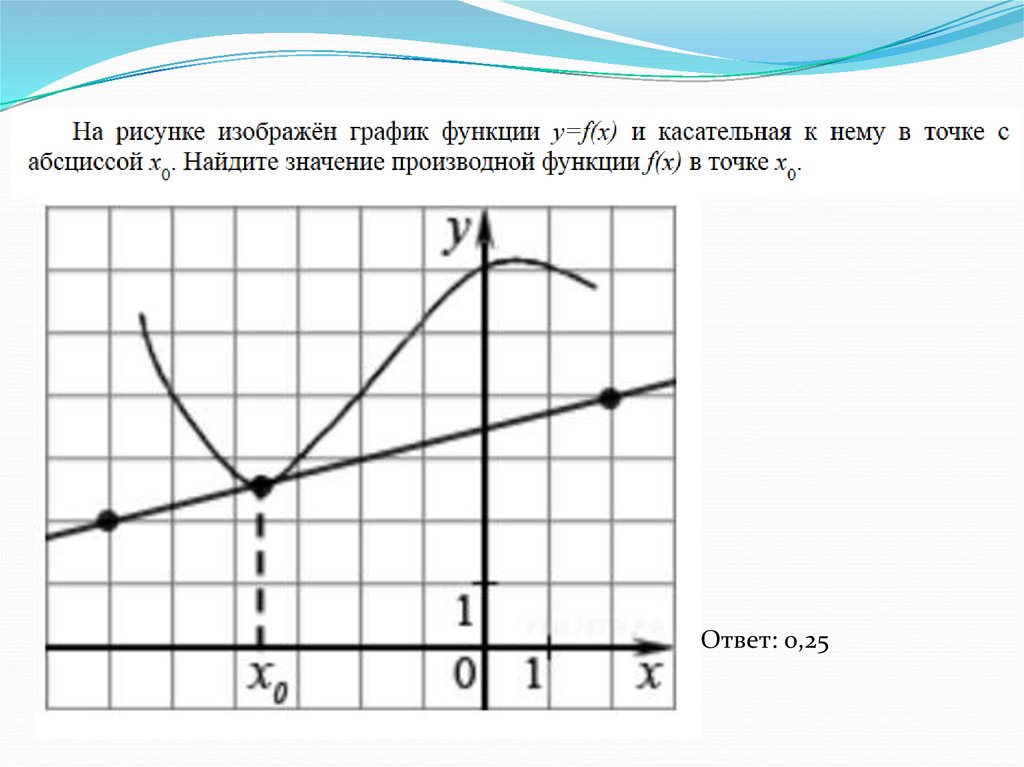
Ответ: 0,25

21.

Домашнее задание
1. Просмотреть и разобрать решение
заданий из презентации
Ссылка https://ppt-online.org/689726
2. Доработать практическую работу
практическую работу. Задания
практической работы выложены в
Вконтакте.
3. Подготовиться к проверочной работе на
сайте Решу ЕГЭ
https://ege.sdamgia.ru/test?theme=68
https://ege.sdamgia.ru/test?theme=70