Similar presentations:
Исходные понятия и определения термодинамики и молекулярной физики
1. Исходные понятия и определения термодинамики и молекулярной физики
2.
Макросистемы – системы, состоящие изочень большого числа частиц (молекул, атомов,
электронов, фотонов и др.). Пример: газ.
Методы изучения макросистем:
• термодинамический
термодинамики);
(лежит
в
основе
• статистический
(лежит
в
основе
молекулярной или статистической физики).
3.
В основе термодинамического методалежат несколько общих законов (их называют
начала термодинамики), которые являются
обобщением опытных фактов. При этом
микроскопическая
картина
не
рассматривается, т.е. можно «забыть» об
атомно-молекулярном строении вещества. При
термодинамическом
методе
изучения
используют понятия и физические величины,
относящиеся к системе в целом. Например,
идеальный газ в состоянии равновесия
характеризуют
объёмом,
давлением
и
температурой.
4.
Статистическийметод
опирается
на
теорию
вероятностей, а в его основе лежат представления
молекулярно-кинетической теории – МКТ, именно: а) атомномолекулярное
строение
вещества;
б)
хаотичность,
беспорядочность теплового движения молекул.
В этом методе для характеристики свойств большого
ансамбля частиц не нужно знать движение каждой из его
частиц. Свойства макросистемы есть суммарный результат
действия всех молекул. Достаточно знать средние величины,
характеризующие движение большой совокупности молекул,
чтобы установить связь между поведением макросистемы в
целом с поведением и свойствами отдельных частиц.
Теория вероятности позволяет находить средние, используя
так называемые функции распределения. Распределение
молекул по скоростям описывается функциями распределения
Максвелла.
5.
Молекулярно-кинетическаятеория идеальных газов
6.
Термодинамика имеет дело с термодинамическойсистемой – совокупностью макроскопических тел, которые
взаимодействуют и обмениваются энергией как между собой,
так и с другими телами (внешней средой).
Состояние макросистемы характеризуют величинами,
которые называют термодинамическими параметрами
(параметрами состояния) Обычно в качестве параметров
состояния выбирают температуру, давление, объем и др.
Если
термодинамические
параметры
имеют
определенные и постоянные значения для любой части
макросистемы, то ее состояние называют равновесным. На
диаграммах состояния (Р−V, V−T, Р−T и др.) равновесное
состояние изображается точкой.
Из неравновесного состояния изолированная система
сама приходит в равновесное состояние спустя время,
которое называется временем релаксации. Если процесс
изменения состояния системы происходит в течение времени,
много большего, чем время релаксации, то такой процесс
можно считать равновесным.
7.
Температура–
физическая
величина,
характеризующая состояние термодинамического
равновесия макросистемы. Если при установлении
теплового контакта между телами, одно из тел
передаёт
энергию
другому
посредством
теплопередачи, то считают, что первое тело имеет
большую температуру, чем второе.
В настоящее время можно применять только
две температурные шкалы – термодинамическую и
Международную практическую, градуированные
соответственно в кельвинах (К) и в градусах Цельсия
(°С).
Температура t по шкале Цельсия связана с
температурой Т по шкале Кельвина:
t = T - 273,15;
8.
В молекулярно-кинетической теории пользуютсяидеализированной моделью идеального газа, согласно
которой:
1) собственный объем молекул газа пренебрежимо мал
по сравнению с объемом сосуда;
2) между молекулами
взаимодействия;
газа
отсутствуют
силы
3) столкновения молекул газа между собой и со
стенками сосуда абсолютно упругие.
Модель идеального газа справедлива для реальных
классических и квантовых газов при достаточно
высоких температурах и разрежениях.
9.
Уравнение состояния идеального газа10.
Междутермодинамическими
параметрами
системы
существует определённая связь, называемая уравнением состояния.
Наиболее простой вид имеет уравнение состояния идеального газа.
Идеальным называют газ, уравнение состояния которого
имеет вид:
m
pV RT ;
pV
M
RT ;
его называют уравнением Менделеева-Клайперона.
m
; - количество вещества, измеряемое числом молей;
где
M
m –масса газа;
M – молярная масса (масса 1 моля);
R = 8,314 Дж/(моль∙К); - универсальная газовая постоянная;
Моль – количество вещества, содержащее число частиц, равное
постоянной Авогадро:
NA= 6,022∙1023 моль-1;
R
23 Дж
k
1,38 10
;
NA
К
- постоянная Больцмана;
11.
Основное уравнение молекулярнокинетической теории идеальных газов12.
Длявывода
основного
уравнения
молекулярно-кинетической теории рассмотрим
идеальный газ. Предположим, что молекулы газа
движутся
хаотически,
число
взаимных
столкновений
между
молекулами
газа
пренебрежимо мало по сравнению с числом
ударов о стенки сосуда, а соударения молекул со
стенками сосуда абсолютно упругие.
Давление с точки зрения МКТ – это средний
импульс,
ежесекундно
передаваемый
поверхности единичной площади в результате
соударений с ней молекул газа. В результате
можно
получить
основное
уравнение
молекулярно-кинетической теории газов:
13.
12
p nm0 v кв ;
3
2
p n E ;
3
или иначе:
14.
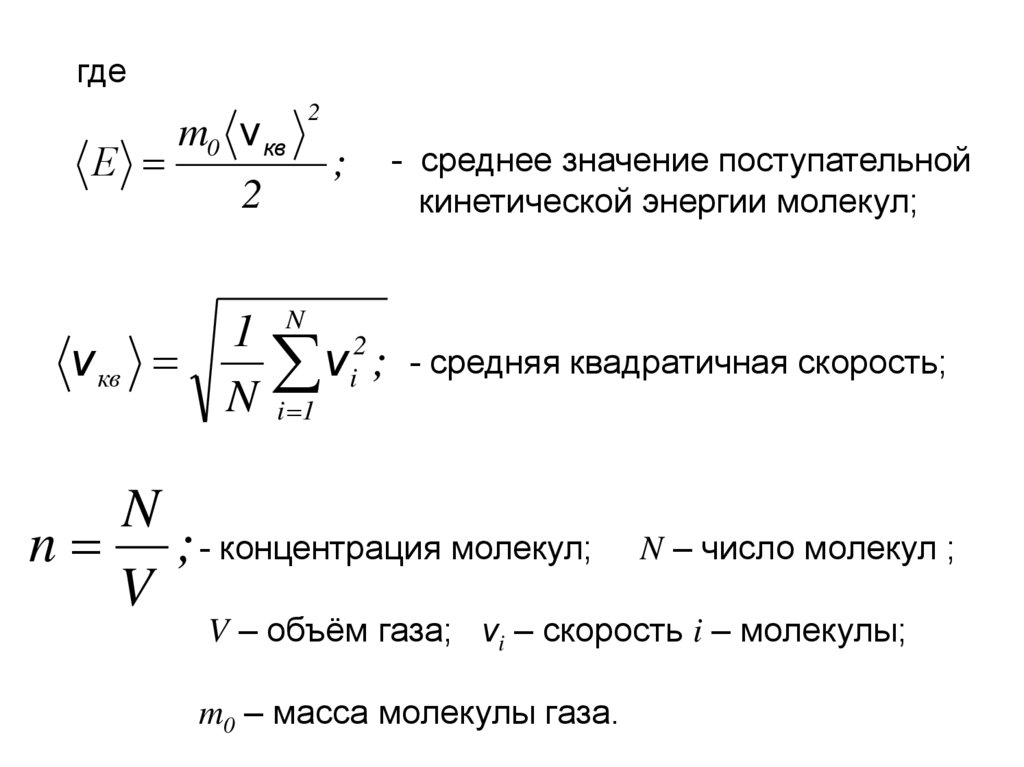
гдеЕ
m0 v кв
v кв
2
2
;
1 N 2
vi ;
N i 1
- среднее значение поступательной
кинетической энергии молекул;
- средняя квадратичная скорость;
N
n ; - концентрация молекул;
V
N – число молекул ;
V – объём газа; vi – скорость i – молекулы;
m0 – масса молекулы газа.
15.
Основное уравнение молекулярно-кинетическойтеории газов раскрывает физический смысл давления:
давление газа на стенку определяется средним
значением поступательной кинетической энергии
молекул.
Сопоставив основное уравнение молекулярнокинетической теории газов с уравнением МенделееваКлайперона получим:
3
Е kT ;
2
где k – постоянная Больцмана.
Эта формула раскрывает физический смысл
температуры Т: температура Т выражает среднюю
кинетическую энергию молекул.
16.
Заменив в выражении2
p n E ;
3
Е
получим:
его выражением
3
Е kT ;
2
p nkT ;
n – концентрация молекул;
Это другая форма уравнения состояния
идеального газа.












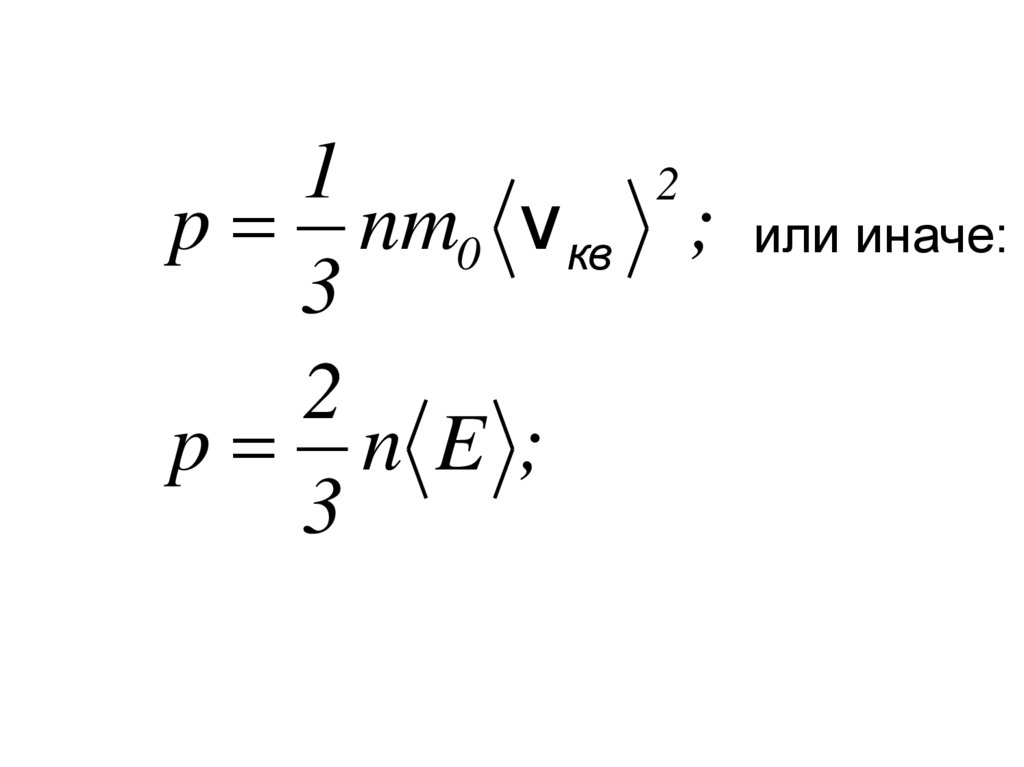


 physics
physics








