Similar presentations:
Углы с сонаправленными сторонами
1.
2.
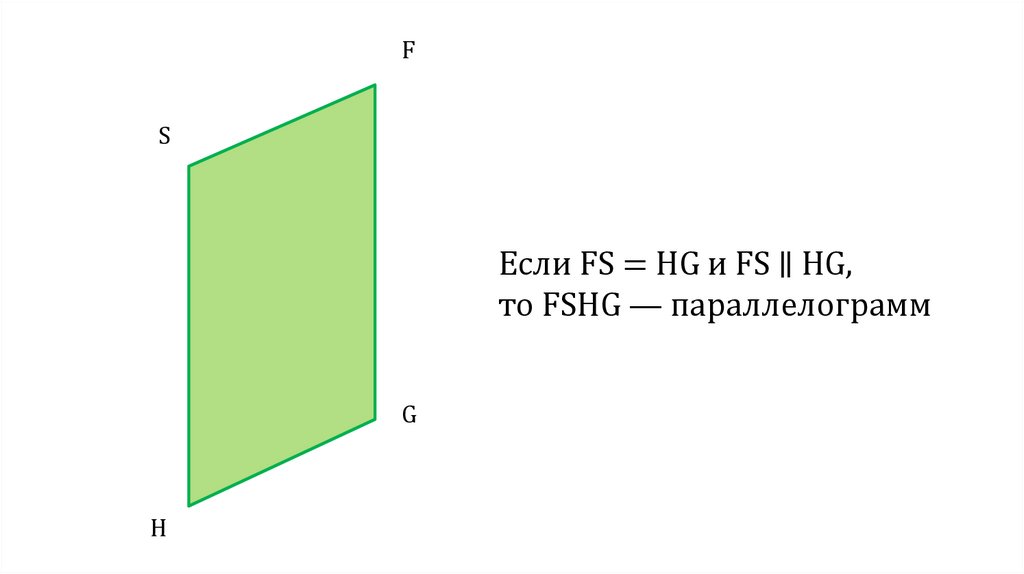
FS
Если FS = HG и FS ∥ HG,
то FSHG — параллелограмм
G
H
3.
АксиомаЛюбая прямая a, лежащая в плоскости,
разделяет плоскость на две части,
называемые полуплоскостями.
Прямая a называется границей каждой
из этих полуплоскостей
4.
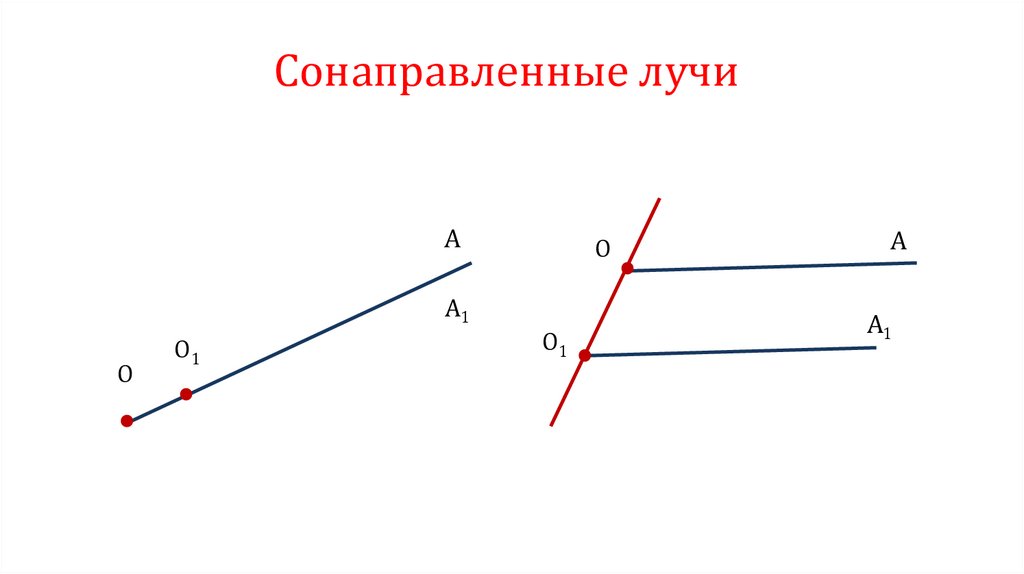
Сонаправленные лучиA
O
A1
O
O1
O1
A
A1
5.
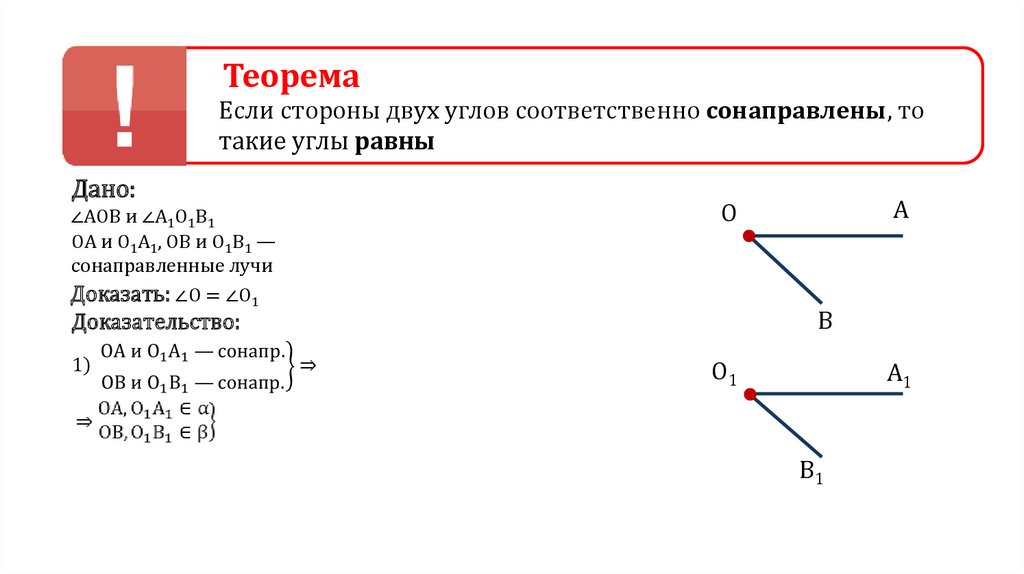
ТеоремаЕсли стороны двух углов
соответственно сонаправлены,
то такие углы равны
6.
ТеоремаЕсли стороны двух углов соответственно сонаправлены, то
такие углы равны
Дано:
∠AOB и ∠А1О1В1
ОА и О1А1, ОВ и О1В1 —
сонаправленные лучи
Доказать: ∠О = ∠О1
A
O
B
Доказательство:
O1
A1
B1
7.
ТеоремаЕсли стороны двух углов соответственно сонаправлены, то
такие углы равны
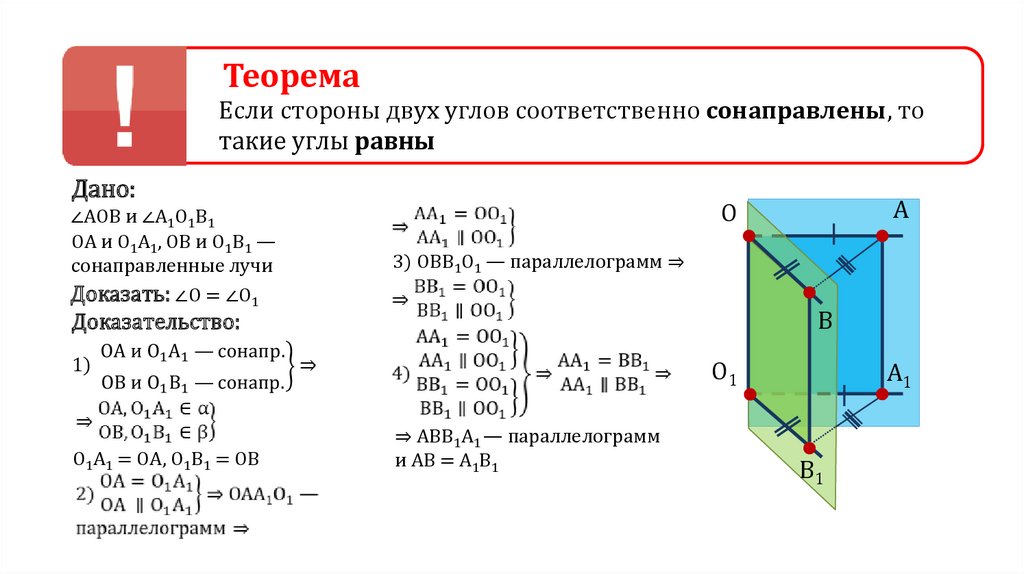
Дано:
∠AOB и ∠А1О1В1
ОА и О1А1, ОВ и О1В1 —
сонаправленные лучи
Доказать: ∠О = ∠О1
A
O
3) OBB1O1 — параллелограмм ⇒
B
Доказательство:
O1
O1A1 = ОA, O1B1 = OB
⇒ ABB1A1 — параллелограмм
и АВ = А1В1
A1
B1
8.
ТеоремаЕсли стороны двух углов соответственно сонаправлены, то
такие углы равны
Дано:
∠AOB и ∠А1О1В1
ОА и О1А1, ОВ и О1В1 —
сонаправленные лучи
Доказать: ∠О = ∠О1
A
O
3) OBB1O1 — параллелограмм ⇒
B
Доказательство:
O1
O1A1 = ОA, O1B1 = OB
⇒ ABB1A1 — параллелограмм
и АВ = А1В1
5) ΔAOB = ΔA1O1B1
(АВ = А1В1, ОA = O1A1, OB = O1B1) ⇒
⇒ ∠О = ∠О1
A1
B1
Теорема доказана
9.
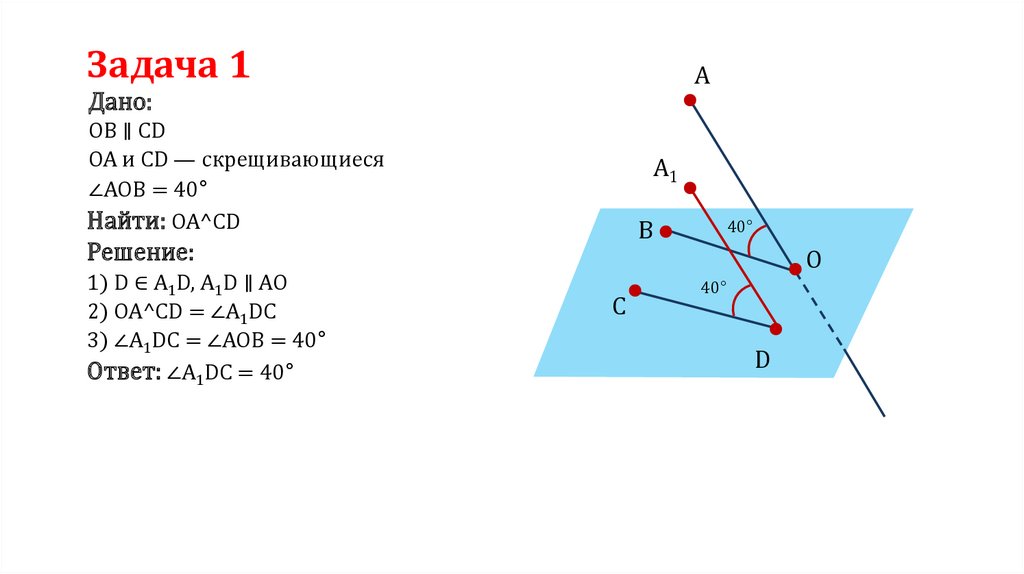
Задача 1A
Дано:
OB ∥ CD
OA и CD — скрещивающиеся
∠AOB = 40°
Найти: OA^CD
A1
B
Решение:
1) D ∈ A1D, A1D ∥ AO
2) OA^CD = ∠A1DC
3) ∠A1DC = ∠AOB = 40°
Ответ: ∠A1DC = 40°
40°
O
C
40°
D
10.
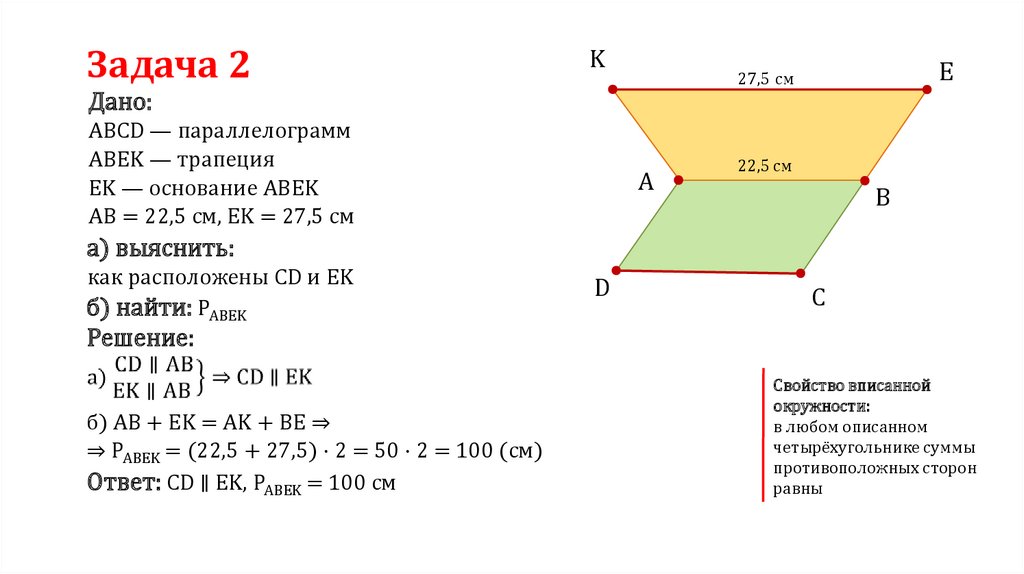
Задача 2K
E
27,5 см
Дано:
ABCD — параллелограмм
ABEK — трапеция
EK — основание ABEK
AB = 22,5 см, EK = 27,5 см
A
22,5 см
B
a) выяснить:
как расположены CD и EK
б) найти: PABEK
D
C
Решение:
б) AB + EK = AK + BE ⇒
⇒ PABEK = (22,5 + 27,5) · 2 = 50 · 2 = 100 (см)
Ответ: CD ∥ EK, PABEK = 100 см
Свойство вписанной
окружности:
в любом описанном
четырёхугольнике суммы
противоположных сторон
равны




 mathematics
mathematics








