Электростатическое поле. Лекции 1, 2

1. Электростатическое поле

Лекции 1,2

2. Электростатическое поле

• Электромагнитное поле – особый вид
материи, является носителем энергии и
обладает характерными
электрическими и магнитными
свойствами
• Электростатическое поле – частный вид
электромагнитного поля, создается
совокупностью неподвижных
электрических зарядов, величина
которых не меняется во времени.

3. Электрический заряд

• Из курса физики известно, что вещество
состоит из элементарных заряженных частиц,
окруженных электромагнитным полем.
• В теории э-м поля рассматривают процессы в
макроскопическом смысле, т.е. рассматривают
общий электрический заряд тела.
Электрические заряды можно считать
бесконечно делимыми и пользоваться
понятиями:
• объемной плотности заряда:
dQ
или q dV
dV
v

4. Электрический заряд

• Из курса физики известно, что вещество
состоит из элементарных заряженных частиц,
окруженных электромагнитным полем.
• В теории э-м поля рассматривают процессы в
макроскопическом смысле, т.е. рассматривают
общий электрический заряд тела.
Электрические заряды можно считать
бесконечно делимыми и пользоваться
понятиями:
• поверхностной плотности заряда:
dQ
или q dS
dS
s

5. Электрический заряд

• Из курса физики известно, что вещество
состоит из элементарных заряженных частиц,
окруженных электромагнитным полем.
• В теории э-м поля рассматривают процессы в
макроскопическом смысле, т.е. рассматривают
общий электрический заряд тела.
Электрические заряды можно считать
бесконечно делимыми и пользоваться
понятиями:
• линейной плотности заряда:
dQ
или q dl
dl
l

6. Электрический заряд

• В основу определения электрического
поля положено его механическое
проявление – закон Кулона
F
q1q 2
4 0 R
2
R 0- единичный вектор,
Где
направленный по линии,
соединяющей заряды.
0 8,86 10 12 ф / м
F
R 0 к
q2
q1
R0

7. Напряженность электростатического поля

F , действующая
• Напряженность поля – сила
на единичный положительный пробный заряд
(q), внесенный в электростатическое поле
заряда Q:
F
E
q
В / м
• Напряженность поля точечного заряда Q:
E
Q
4 0 R
2
R 0 В / м

8. Принцип суперпозиции электрических полей

• Если поле создано несколькими
электрическими зарядами, то
напряженность результирующего поля в
каждой точке равна векторной сумме
напряженностей от каждого из зарядов в
отдельности
n
Е Е1 Е 2 ... Е n
i 1
Ei

9. Графическое представление поля

• Электростатическое поле изображают с
помощью линий напряженности поля или
силовых линий поля. Эти линии проводят
так, чтобы касательные к ним в каждой точке
пространства совпадали с вектором
напряженности в данной точке. Линии
напряженности никогда не пересекаются.
• Величину напряженности поля
характеризуют числом линий
напряженности,пронизывающих единицу
поверхности, перпендикулярной линиям.

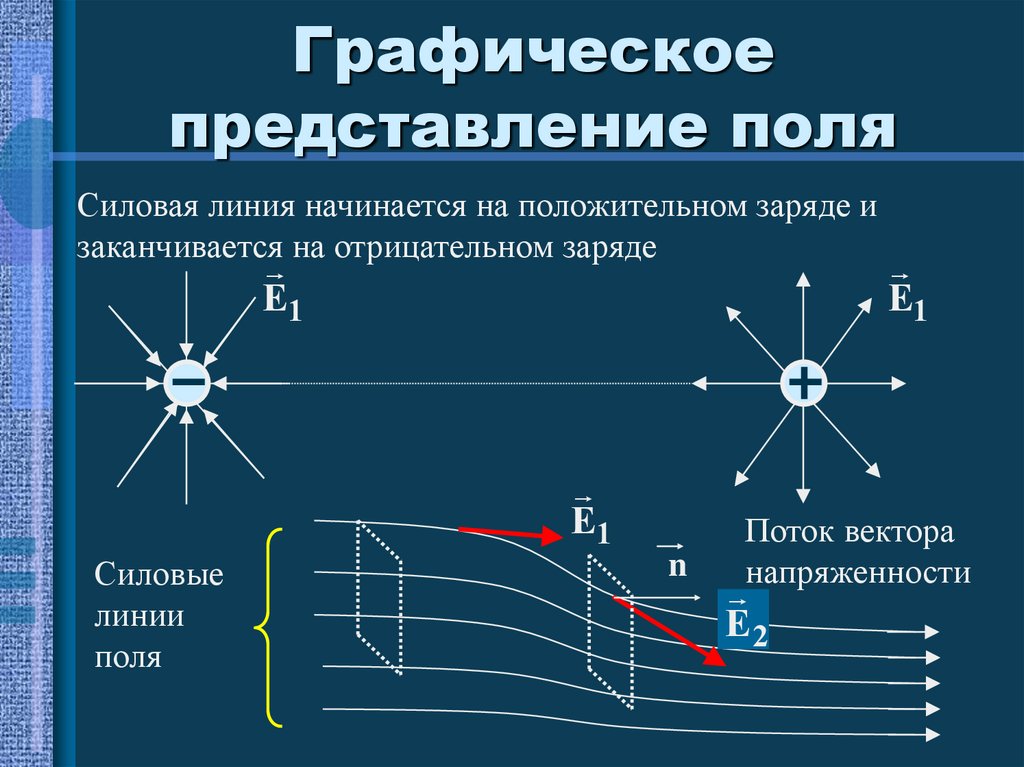
10. Графическое представление поля

Силовая линия начинается на положительном заряде и
заканчивается на отрицательном заряде
E1
E1
Силовые
линии
поля
n
E1
Поток вектора
напряженности
E2

11. Поток вектора напряженности поля

• - это число линий напряженности, пронизывающих элементарную площадку dS, нормаль
n к которой образует угол с вектором E
dФ E E dS n
dS n - Вектор, модуль которого равен dS, а направление
совпадает с нормалью к площадке.
E Для произвольной замкнутой
поверхности:
En
n
ФE
E dS n
s
Поток вектора Е – скалярная величина

12. Теорема Гаусса (в вакууме)

E1
Поток вектора напряженности сквозь
сферическую поверхность радиуса r,
охватывающую точечный заряд
Q,
находящийся в ее центре:
Q
Ф E E n dS
4 r
2
0
4 0r
S
Q
2
Если окружить сферу замкнутой поверхностью
произвольной формы, то каждая линия напряженности,
пронизывающая сферу, пройдет и сквозь эту поверхность.

13. Теорема Гаусса (в вакууме)

E1
Поток вектора напряженности сквозь
сферическую поверхность радиуса r,
охватывающую точечный заряд
Q,
находящийся в ее центре:
Q
Ф E E n dS
4 r
2
0
4 0r
S
Q
2
Если замкнутая поверхность не охватывает заряд, то поток
сквозь нее равен нулю, так как число линий
напряженности, входящих в поверхность, равно числу
линий напряженности, выходящих из нее.

14. Теорема Гаусса (в вакууме)

• Общая формулировка теоремы Гаусса:
• Поток вектора напряженности
электростатического поля в вакууме
через произвольную замкнутую
поверхность равен алгебраической сумме
заключенных внутри этой поверхности
зарядов, деленной на 0 .
1
Ф E En dS
0
S
n
i 1
1
Qi
dV
0
v

15. Вектор электрического смещения

• Вектор электрического смещения
(электрической
индукции) в вакууме:
• Вектор D совпадает по направлению с Е
D 0E
Теорема Остроградского-Гаусса:
Поток вектора электрического смещения в
вакууме через произвольную замкнутую
поверхность равен алгебраической сумме
заключенных внутри этой поверхности зарядов
Ф D D n dS 0 En dS
S
S
n
Qi dV
i 1
v

16. Циркуляция вектора напряженности электростатического поля

Точечный
заряд
перемещает
ся из 1 в 2
по перемещению
заряда в пути:
•Работа
Работа
на элементарном
F
q
1
dl
r
r1
r2
электростатическом поле зависит только
от положения начальной и конечной
1 qQ
точки
и
не
зависит
от траектории
dA Fdl cos
dl cos
2
4 0 r
движения.
так
как dl cos dr ,полето
Электростатическое
2
ПОТЕЦИАЛЬНОЕ,
1 qQ
dA
dr
2
4 0 r
Электростатические
силы КОНСЕРВАТИВНЫ
Работа
по перемещени ю заряда из 1 в 2
r2
A12
Q
Заряд,
создающий
поле
r1
qQ
dA
4 0
r2
r1
dr
1
r 2 4 0
qQ qQ
r2
r1

17. Циркуляция вектора напряженности электростатического поля

В ПОТЕНЦИАЛЬНОМ
• РАБОТА
РаботаСИЛ
на элементарном
пути:
Точечный
заряд
перемещает
ся из 1 в 2
F
1
dl
r
r1
ПОЛЕ ВДОЛЬ ЗАМКНУТОГО КОНТУРА
РАВНА НУЛЮ
1 qQ
dA Fdl cos
dl cos
2
dA 4 q0 rEdl 0
так как dl cos dr , то
L
L
2
1 qQ
dA
dr
Этот интеграл называется –
2
4
Edl 0 r ЦИРКУЛЯЦИЯ ВЕКТОРА
Работа по перемещени
ю заряда из 1 в 2
НАПРЯЖЕННОСТИ
L
r2
A12
Q
Заряд,
создающий
поле
r1
qQ
dA
4 0
r2
r1
dr
1
r 2 4 0
qQ qQ
r2
r1

18. Безвихревой характер электростатического поля

Edl 0
Циркуляция вектора напряженности
электростатического поля равна 0
L
Используя теорему Стокса , можно записать
Edl rot E dS
L
S
Так как циркуляция вектора напряженности электростатического поля равна 0, то и ротор равен нулю:
rot E 0
Электростатического поле - безвихревое

19. Потенциал электрического поля

• Тело, находящееся в потенциальном поле
обладает потенциальной энергией, за счет
которой силами поля совершается работа.
• Работу сил электростатического поля можно
представить как разность потенциальных
энергий, которыми обладает точечный заряд в
начальной и конечной точках.
1 qQ qQ
U1 U 2
A 12
4 0 r1
r2
Потенциальная энергия заряда q в
поле заряда Q:
С-произвольная константа
qQ
U
C
4 0r

20. Потенциал электрического поля

При r C 0 , потенциаль ная энергия поля :
Qq
U
4 0r
U
Отношение
не зависит от величины пробного заряда q
q
и является энергетиче ской характерис тикой поля ,
U
называемой потенциало м :
q
Потенциал в произвольной точке электростатического
поля – физическая величина, определяемая потенциальной
энергией единичного положительного заряда, помещенного
в эту точку. Единица потенциала [B]= [Дж]/[К].

21. Потенциал электрического поля

• Потенциал поля, созданного несколькими
зарядами равен алгебраической сумме
потенциалов полей всех этих зарядов.
n
U
Ui
i 1
Потенциал – скалярная энергетическая
характеристика поля.
Напряженность – векторная силовая
характеристика поля

22. Напряженность поля как градиент потенциала

• Работа по перемещению единичного
заряда из точки 1 в точку 2 вдоль оси X
1
1
E
Ex
dx
2
2
d
1 2 d E x dx или E x
dx
d
Производная
выражает быстроту
dx
изменения потенциала в направлении по оси х.
Повторив аналогичные рассуждения для осей y и z, получим:
d d d
E
i
j
k , где i , j , k единичные вектора
dy
dz
dx

23. Напряженность поля как градиент потенциала

E
i
j
k , где i , j , k единичные вектора
y
z
x
Где оператор набла:
x i y j z k
Градиентом скалярной величины в векторном анализе
называют вектор, направление которого совпадает с
направлением быстрейшего увеличения величины .
Знак
минус означает,
что вектор напряженности
поля всегда
Напряженность
электрического
поля равна градиенту
направлен
в сторону
убывания
потенциала.
потенциала
с обратным
знаком:
E grad

24. Силовые и эквипотенциальные линии поля

Для графического изображения распределения потенциала
электростатического поля пользуются эквипотенциальными
поверхностями – поверхностями, во всех точках которых
потенциал имеет одно и то же значение.
Так как все точки эквипотенциальных поверхностей имеют
одинаковый потенциал, то работа по перемещению пробного
единичного заряда вдоль этих поверхностей всегда равна нулю,
следовательно сила, действующая на заряд направлена
перпендикулярно траектории движения (эквипотенциальной
поверхности).
Таким образом силовые линии напряженности поля всегда
направлены нормально к эквипотенциальной поверхности

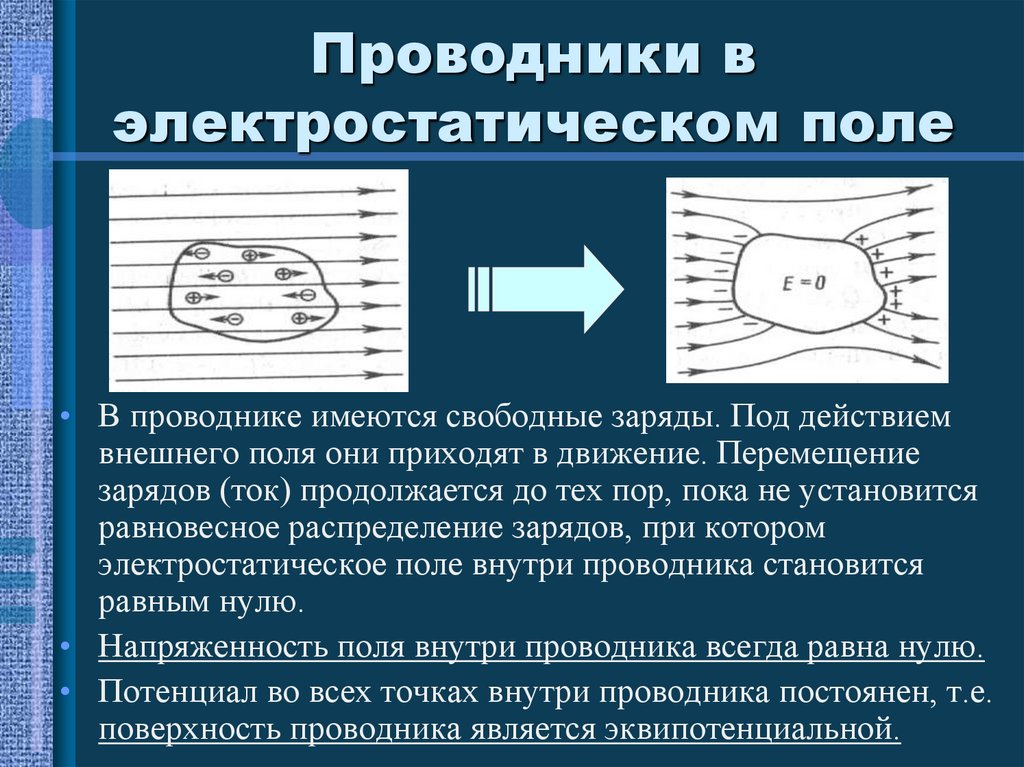
25. Проводники в электростатическом поле

• В проводнике имеются свободные заряды. Под действием
внешнего поля они приходят в движение. Перемещение
зарядов (ток) продолжается до тех пор, пока не установится
равновесное распределение зарядов, при котором
электростатическое поле внутри проводника становится
равным нулю.
• Напряженность поля внутри проводника всегда равна нулю.
• Потенциал во всех точках внутри проводника постоянен, т.е.
поверхность проводника является эквипотенциальной.

26. Проводники в электростатическом поле

• Если проводящее тело внутри полое, то в
полости электростатическое поле также
отсутствует. Это используют для
электростатического экранирования.
Для защиты от внешних полей
измерительные приборы, радиоэлектронные
схемы помещают в замкнутые
металлические оболочки, называемые
экранами.
Часто экраны выполняют из мелкой сетки и
заземляют, чтобы потенциал экрана был
равен 0.
Свинцовая оболочка кабеля также выполняет
роль экрана
Конструкция кабеля

27. Поляризация диэлектриков

+++++
------+++ +++
• В отсутствие электрического поля
диэлектрик нейтрален
• Приблизим к электрометру
стеклянную пластину. Показания
электрометра уменьшатся. Отсюда
можно сделать вывод:
• На диэлектрике в электрическом
поле возникают заряды. Причем на
ближайшей к заряженному телу
части диэлектрика появляются
заряды противоположного знака, а
на удаленной части диэлектрика
возникают одноименные заряды
Это явление называют
поляризацией
диэлектриков

28. Свободные и связанные заряды.

• Свободными называют заряды, которые под
воздействием сил поля могут свободно
перемещаться в веществе, их перемещение не
ограничивается внутримолекулярными силами.
Свободные заряды имеются в проводниках
• Связанными зарядами называют заряды,
связанные с молекулами вещества. Эти заряды
при воздействии внешнего поля могут
незначительно перемещаться внутри молекул.
Связанные заряды имеются в диэлектриках.

29. Поляризация диэлектриков

+++++
------+++ +++
• Поляризация диэлектрика –
это упорядоченное
изменение расположения
связанных зарядов в теле,
вызванное электрическим
полем.

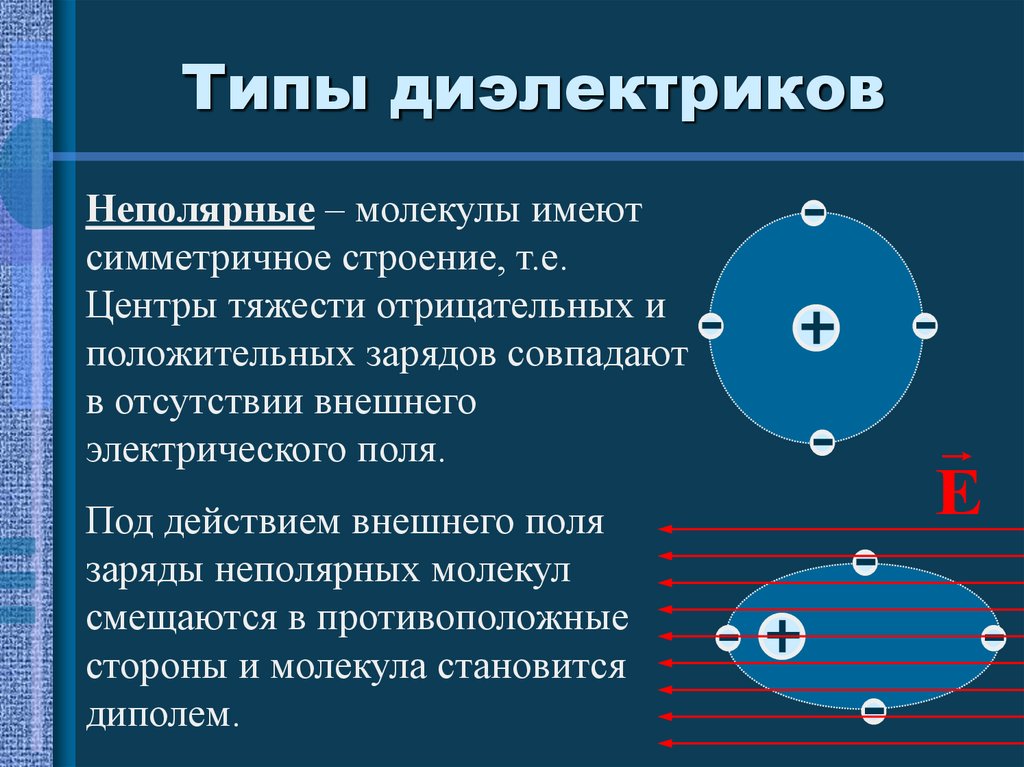
30. Типы диэлектриков

Неполярные – молекулы имеют
симметричное строение, т.е.
Центры тяжести отрицательных и
положительных зарядов совпадают
в отсутствии внешнего
электрического поля.
Под действием внешнего поля
заряды неполярных молекул
смещаются в противоположные
стороны и молекула становится
диполем.
E

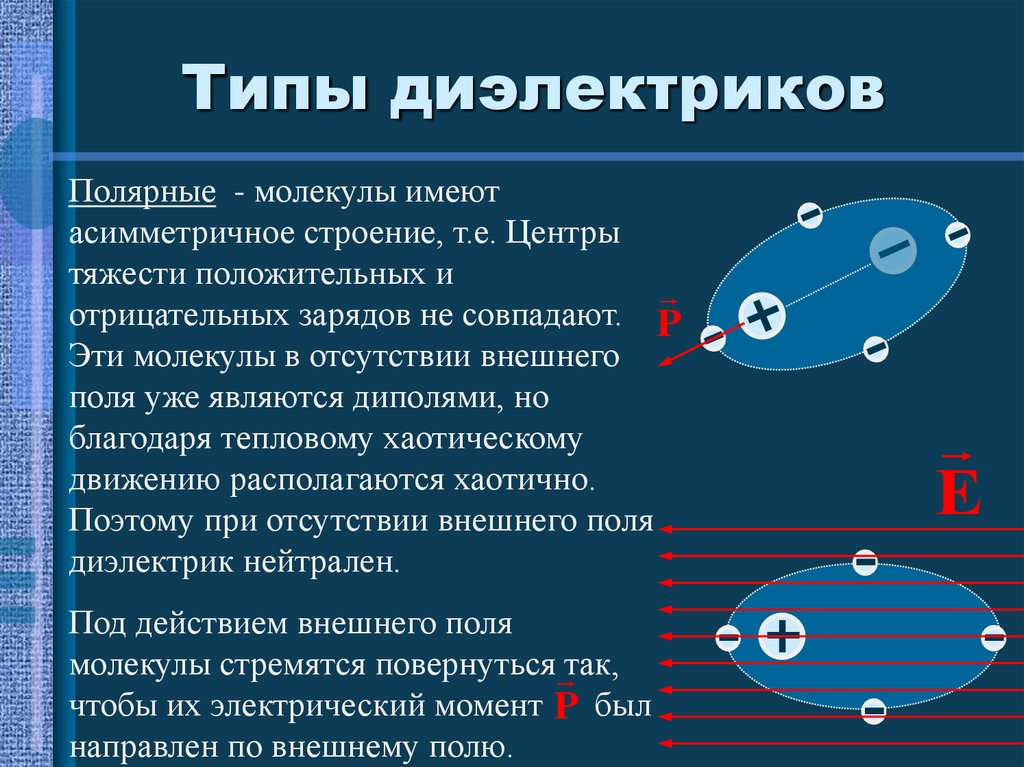
31. Типы диэлектриков

Полярные - молекулы имеют
асимметричное строение, т.е. Центры
тяжести положительных и
отрицательных зарядов не совпадают. P
Эти молекулы в отсутствии внешнего
поля уже являются диполями, но
благодаря тепловому хаотическому
движению располагаются хаотично.
Поэтому при отсутствии внешнего поля
диэлектрик нейтрален.
Под действием внешнего поля
молекулы стремятся повернуться так,
чтобы их электрический момент P был
направлен по внешнему полю.
E

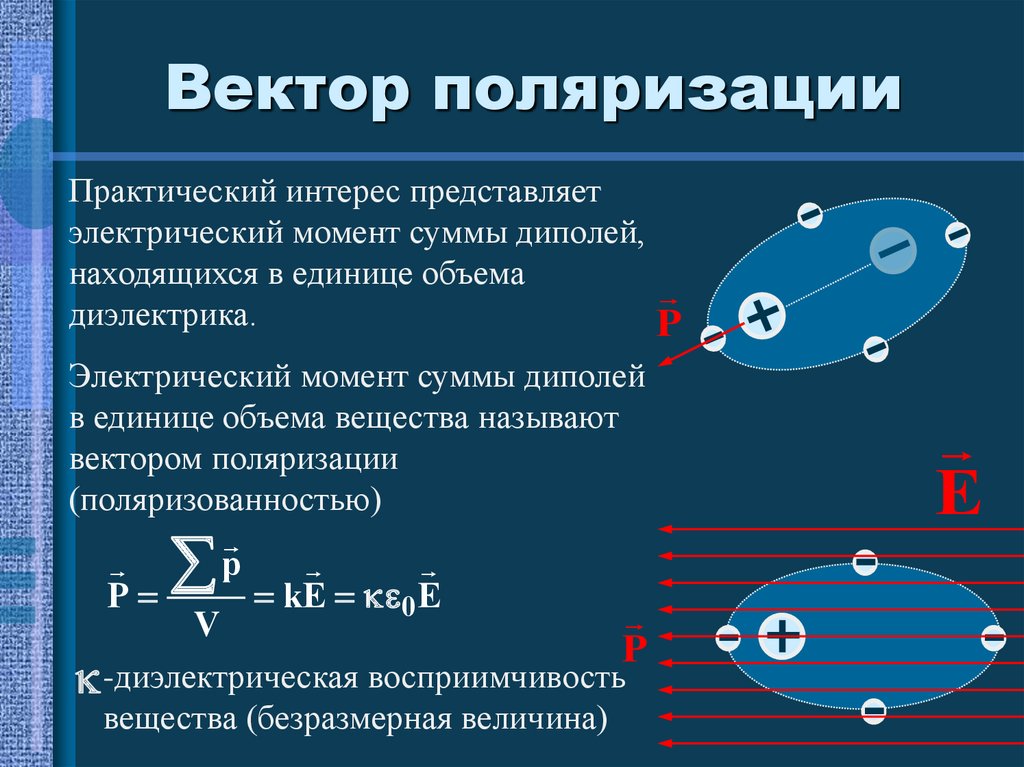
32. Вектор поляризации

Практический интерес представляет
электрический момент суммы диполей,
находящихся в единице объема
диэлектрика.
P
Электрический момент суммы диполей
в единице объема вещества называют
вектором поляризации
(поляризованностью)
P
V
p
kE 0 E
P
-диэлектрическая восприимчивость
вещества (безразмерная величина)
E

33. Вектор электрического смещения в диэлектриках

• Связанные заряды в
диэлектрике, помещенном во
внешнее электрическое поле
создают свое внутреннее
поле, напряженность которого
будет направлена
противоположно
напряженности внешнего
поля. Поэтому напряженность
результирующего поля в
диэлектрике будет меньше ,
чем напряженность внешнего
поля.
Eвне ш
E внут
E ре з E вне ш E внут

34. Вектор электрического смещения в диэлектриках

Вектор электрического
смещения в диэлектриках
В результате часть линий
напряженности внешнего поля
обрывается на связанных
зарядах в диэлектрике.
E внут
Eвне ш
Другая часть линий
напряженности проходит
сквозь диэлектрик.
• Таким образом вектор
напряженности поля на
границе раздела вакуумдиэлектрик изменяется
скачкообразно.

35. Вектор электрического смещения в диэлектриках

•Поэтому оказалось целесообразным
ввести еще одну характеристику поля –
вектор электрического смещения,
E внут
который равен сумме двух векторов:
Eвне ш
D ре з 0 E P 0 (1 )E
обозначим 1 , тогда D ре з 0 E
относитель ная диэлектрич еская проницаемость
Вектор D не зависит от свойств среды в отличие от вектора E.
Он описывает электростатическое поле, создаваемое
свободными зарядами, но при таком их распределении в
пространстве, какое имеется при наличии диэлектрика.

36. Линии электрического смещения

Поле вектора D изображается с помощью
линий электрического смещения, направление
и густота которых характеризуют поле.
Линии вектора E могут начинаться и
заканчиваться на любых зарядах – свободных и
связанных.
Линии вектора D начинаются и заканчиваются
только на свободных зарядах.
Через области, где находятся
связанные
заряды, линии вектора D проходят не
прерываясь.

37. Теорема Гаусса (в интегральной форме)

• Поток вектора электрического смещения сквозь
произвольную замкнутую поверхность равен
алгебраической сумме свободных
электрических зарядов, заключенных внутри
этой поверхности.
Ф D D n dS
S
n
Qi dV
i 1
v

38. Теорема Гаусса (в дифференциальной форме)

• Разделим обе части уравнения на одну и ту же
скалярную величину – объем V:
n
DndS Qi dV
S
V
i 1
V
v
V
DndS
• Найдем предел выражения при V
0: lim
v 0
S
V
Предел отношения потока векторной величины сквозь
замкнутую поверхность, ограничивающую некоторый объем
к объему называют дивергенцией (истоком) вектора (div D).
div D
ТЕОРЕМА ГАУССА В
ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ

39. Определение дивергенции векторной функции

E x E у E z
По определени ю div E
,
x
y
z
Покажем , что скалярное умножение
оператора
на векторную функцию E , означает взятие
дивергенци и от этой векторной функции :
E x E у E z
E i
j
k i Ex j E y kE z
,
y
z
x
y
z
x
при этом учитываем что скалярное произведен ие
х ортов равно
ых 0 :
одноименны
1, а разноименн
i i j j k k 1 1 cos 0 1 , i j i k j k 1 1 cos( / 2) 0
Таким образом можно
записать
:
E div E

40. Теорема Гаусса (в дифференциальной форме)

div D
ТЕОРЕМА ГАУССА В
ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
(первая форма записи)
div E
0
ТЕОРЕМА ГАУССА В
ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
для однородной и изотропной среды
(вторая форма записи)
своб связ
div E
0
ТЕОРЕМА ГАУССА В
ДИФФЕРЕНЦИАЛЬНОЙ ФОРМЕ
для неоднородной среды
(третья форма записи)

41. Уравнения Пуассона и Лапласа для электростатического поля

Получены уравнения:
div E
0
E grad
div grad
После подстановки, получим:
0
Дивергенцию градиента называют лапласианом (оператором
Лапласа) и обозначают:
2
Уравнение Пуассона
В тех точках поля, где нет зарядов –
уравнение Лапласа
2
x
2
2
y
2
0
2
2 0
2
z 2

42. Общее решение уравнения Пуассона

• Пусть в объеме V имеются точечные объемные,
поверхностные, и линейные заряды: dv , ds , dl
• Потенциал в некоторой точке пространства
складывается из трех составляющих:
От объемного заряда
dv
4 0 R
От поверхностного заряда
От линейного заряда
ds
4 0 R
dl
4 0 R
Полное значение потенциала в точке пространства
1
4 0
dv
1
V R 4 0
ds
1
S R 4 0
L
dl
R

43. Теорема единственности решения

• Покажем, что если найдена напряженность электрического
поля, которая удовлетворяет уравнению Лапласа-Пуассона и
заданным граничным условиям, то это решение единственное . Допустим, что есть два решения Е1 и Е 2 .
Тогда для Е1 div(ε 0εE 1 ) ρ и rotE1 0
и для
Е 2 div(ε 0εE 2 ) ρ и rotE 2 0
Найдем дивергенци ю и ротор разности E1 E 2 :
div(E1 E 2 ) divE1 divE 2 0
rot(E1 E 2 ) rotE1 rotE 2 0
Если у вектора E1 E 2 и дивергенци я и ротор равны 0,
то такой вектор сам равен нулю, т.е. E1 E 2 0, а E1 E 2
оба решения одинаковы.

44. Граничные условия в электростатическом поле (1)

1
2
Рассмотрим границу двух непроводящих сред,
диэлектрические проницаемости которых 1
и 2 .
Пусть на границе двух сред имеется свободный заряд с поверхностной плотностью .
Построим замкнутую цилиндрическую
поверхность, пересекающую поверхность
раздела двух сред. По теореме Гаусса:
D ds D1 ds D2 ds D ds S
s
s
s
sбок

45. Граничные условия в электростатическом поле (1)

1
При S 0 можно считать , что
D1 ds D1n S
s
2
и
D2 ds D2n S
s
При малой высоте цилиндра можно считать ,
что поток через боковую поверхност ь 0.
Тогда D1n S D 2 n S S, отсюда
1 ое граничное условие :
D1n D 2 n или 1E1n 2 E 2 n
Нормальная составляющая вектора электрической индукции
на границе двух непроводящих сред изменяется скачком,
равным поверхностной плотности зарядов, распределенных
на границе.

46. Граничные условия в электростатическом поле (1)

1
При S 0 можно считать , что
D1 ds D1n S
s
2
и
D2 ds D2n S
s
При малой высоте цилиндра можно считать ,
что поток через боковую поверхност ь 0.
Тогда D1n S D 2 n S S, отсюда
1 ое граничное условие :
D1n D 2 n или 1E1n 2 E 2 n
Если поверхностная плотность зарядов равна 0, то:
D1n D 2 n или 1E1n 2 E 2 n
Нормальная составляющая вектора D непрерывна.

47. Граничные условия в электростатическом поле (2)

1
2
Проведем замкнутую линию L так,
чтобы одна ее часть находилась в первом
диэлектрике, а друга во втором.
Зададимся направлением обхода по
контуру 1-2-3-4 и составим циркуляцию
вектора напряженности.
В электростатическом поле циркуляция
вектора напряженности равна 0:
12
E1dl Edl
23
E 2dl Edl 0
34
41
при dl 0 можно считать Е const, тогда
E1dl E1 l и
E12dl E 2 l
12
34

48. Граничные условия в электростатическом поле (2)

1
E1dl
12
Edl
23
E 2dl Edl 0
34
(1)
41
при dl 0 можно считать Е const, тогда
E1dl E1 l и
E12dl E 2 l
12
34
Если отрезки 2 3 и 4 1 уменьшать так ,
чтобы они 0 , то отрезки l совпадут с
граничной поверхност ью и Edl Edl 0
2
23
41
На границе двух непроводящих сред касательные составляющие
тогда (1) можно записать в виде
вектора напряженности электрического
поля
а
E1
l E 2равны,
l
0
,
потенциал непрерывен.
отсюда второе граничное условие
1 2
E1 E 2 или
D1 D 2
1
2

49. Условия на границе раздела двух диэлектриков

1. Нормальная составляющая вектора электрической индукции
на границе двух непроводящих сред изменяется скачком,
равным поверхностной плотности зарядов, распределенных на
границе.
D1n D 2 n или 1E1n 2 E 2 n
2. Если поверхностная плотность зарядов равна 0, то
нормальная составляющая вектора D непрерывна.
D1n D 2 n или 1E1n 2 E 2 n
3. Касательные составляющие вектора напряженности
электрического поля равны:
D1 D 2
E1 E 2 или
а потенциал непрерывен: 1 2
1
2
,

50. Условия на границе раздела проводящего тела и диэлектрика

В проводящей среде векторы поля равны нулю, а потенциал
всех точек проводника один и тот же. Если первая среда
диэлектрик, а вторая – проводник, то граничные условия:
E 2 0 , D 2 0 , 2 const,
D1n D1 или 1E1 ,
E1 0 или D1 0 .

51. Электрическая емкость

• Емкость C между двумя телами, на которых
имеются равные по величине и противоположные
заряды есть абсолютная величина отношения заряда
на одном теле к напряжению между телами:
Q
ф ,
C
U
1 кулон
1 фарада [ф]
1 вольт

52. Электрическая емкость

• В системе нескольких заряженных тел потенциал каждого тела определяется не только зарядом данного тела, но и зарядами всех остальных тел.
Возможны 2 случая:
Если тело А2 мало, то
можно пренебречь
q2
q2
искажением поля ,
возникающим от
индуцированных зарядов
на этом теле.
В общем случае потенциал U1 определяется как зарядом, распределенным на теле А1, так и зарядами, индуцированными на теле А2.
1.
2.
Если заряды обоих тел отличны от нуля, то потенциалы тел могут быть
найдены на основе принципа наложения:
U1 U1 U1 11q1 12q 2
U U U q q
2
2
2
21 1
22 2

53.

Электрическая емкость
В общем случае, когда имеется n заряженных тел:
U1 11q1 12q 2 ... 1k q k ... 1n q n
U 2 21q1 22q 2 ... 2 k q k ... 2 n q n
U k k1q1 k 2q 2 ... kkq k ... knq n
U n n1q1 n 2q 2 ... nkq k ... nnq n
kk собственны е потенциаль ные коэффициенты .
kn взаимные потенциаль ные коэффициенты

54.

Электрическая емкость
Часто выражают заряд каждого тела через разности
потенциалов данного тела и других тел, в том числе
и земли:
q1 С11 ( U 1 0) C12 ( U 1 U 2 ) ... C1k ( U 1 U k ) ... C1n ( U 1 U n )
q k C k1 ( U k U 1 ) C k 2 ( U k U 2 ) ... C kk ( U k 0) ... C kn ( U k U n )
q n C n1 ( U n U 1 ) C n 2 ( U n U 2 ) ... C nk ( U n U k ) ... C nn ( U n 0)
C kk собственные емкости,
С kn взаимные емкости

55. Энергия взаимодействия точечных заряженных тел

• При перемещении точечного заряда Q1 из
точки 1 в бесконечность необходимо
совершить работу, против сил поля.
1
Fdl E1Qdl Q1 E1dl Q1 1
1
1
• Энергия взаимодействия двух зарядов Q1 и
Q 2.
2
Q1 1 Q 2 2
W
2
1
2
Qn n
n 1

56. Энергия электростатического поля

Если поле возбуждается объемными и поверхност ными зарядами ,
то элементарн ые заряды dQ dv и dQ ds можно считать
точечными.
ED
Энергия поля : W 2 dv 2 ds
dv .
2
v
s
v
В однородных и изотропных средах D 0 E , тогда энергия поля :
0 E 2
W
dv
2
v
Физический смысл этого уравнения заключаетс я в том , что носителем
энергии является электричес кое поле, распределе нное
dW ED 0 E 2
в пространстве с объемной плотностью :
dv
2
2