Similar presentations:
Функция, её свойства и график
1. ___.01.22 г.
Функция у ах вх с ,её свойства и график
2
2. Пример 1. Построить график функций
у 3х 6 х 12
у 3( х 2 х) 1
2
3(( х 2 х 1) 1) 1
2
3( х 1) 3 1
2
3( х 1) 4
2
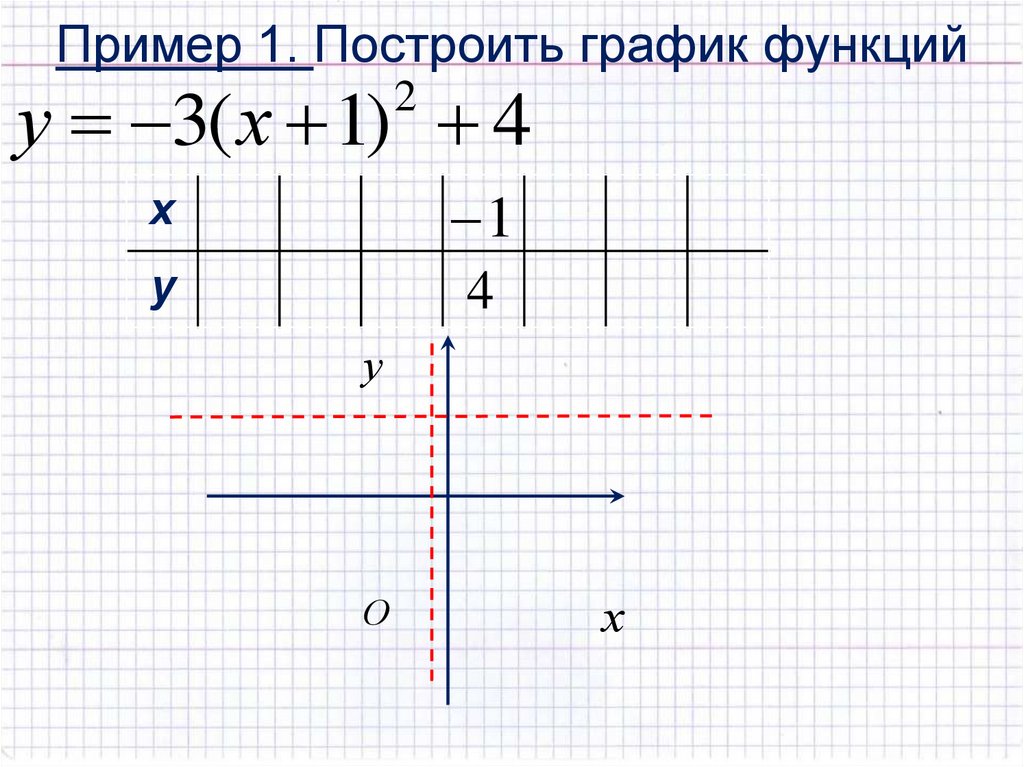
3. Пример 1. Построить график функций
у 3( х 1) 42
х
1
у
4
у
О
х
4. Теорема
Графиком квадратичной функции2
у ах вх с является парабола,
которая получается из параболы
2
у ах параллельным переносом
5. Доказательство:
22выделения полного
Воспользуемся
методом
у ах вх с (ах вх) с
квадрата.
в Имеем:
2
а( х х) с
2
2
а в
в
в
2
а(( х 2 х 2 ) 2 ) с
2а 2 4 а
4а
в 2 в
а( х ) с
2а
4а
2
в 2 4ас в
а( х )
.
2а
4а
6. Доказательство:
Итак, нам удалось преобразовать2
квадратный трёхчлен ах вх с к виду
2
у а( х l ) m , где
в 2 4ас в
у а( х )
.
2а
4а
2
l
m
Вершина параболы О(0; 0) сместилась
параллельным переносом в точку (-l; m)
7.
Обратите внимание, что вершиной сталаточка (-l; m), значит осью параболы
в
является прямая х = -l, т.е. х
2а
в 2 4ас в
у а( х )
.
2а
4а
2
l
m
8.
Итак, осью параболы у ах вх св
является прямая х
;
2а
х0 абсцисса вершины
вычисляется именно по этой
формуле
2
9. Пример 2. Не выполняя построения графика функции ответьте на вопросы:
у 3х 6 х 12
1) Какая прямая служит осью параболы?
10. Пример 2. Не выполняя построения графика функции ответьте на вопросы:
у 3х 6 х 12
2) Каковы координаты вершины
параболы?
11. Пример 2. Не выполняя построения графика функции ответьте на вопросы:
у 3х 6 х 12
3) Куда направлены ветви параболы?
12.
На уроке:1) Новая тема – 15 минут
2) §24: №1 - 4 устно, 5 - 6(а, б), 11(б),12 (г)
Дома:
§24: № 5 - 6 (а, б), 7 (а), 8 (б), 10 (а), 11 (а),
12 (б)











 mathematics
mathematics








