Функции

1. ФУНКЦИИ

Свойства функций
Домашнее задание
Учебник: с.252-253 – читать;
Выполнить № 778; 780(а, б); 785(б).

2. Цель нашего урока

• графики реальных зависимостей,
• практические работы, вопросы и
задачи прикладного и
практического характера.
• моделировать с помощью
изучаемых функций самые
разнообразные реальные
ситуации.
• описывать свойства функции на
основе её графического
представления.
• читать графики реальных
зависимостей.
Как мы считываем
информацию с графиков
реальных зависимостей? Если
мы имеем дело с графиком, то
ищем на нём верхнюю и
нижнюю точки. Кроме того,
смотрим, где график
располагается выше
горизонтальной оси, а где —
ниже. Наконец, нас интересуют
промежутки, на которых график
поднимается вверх или
опускается вниз.

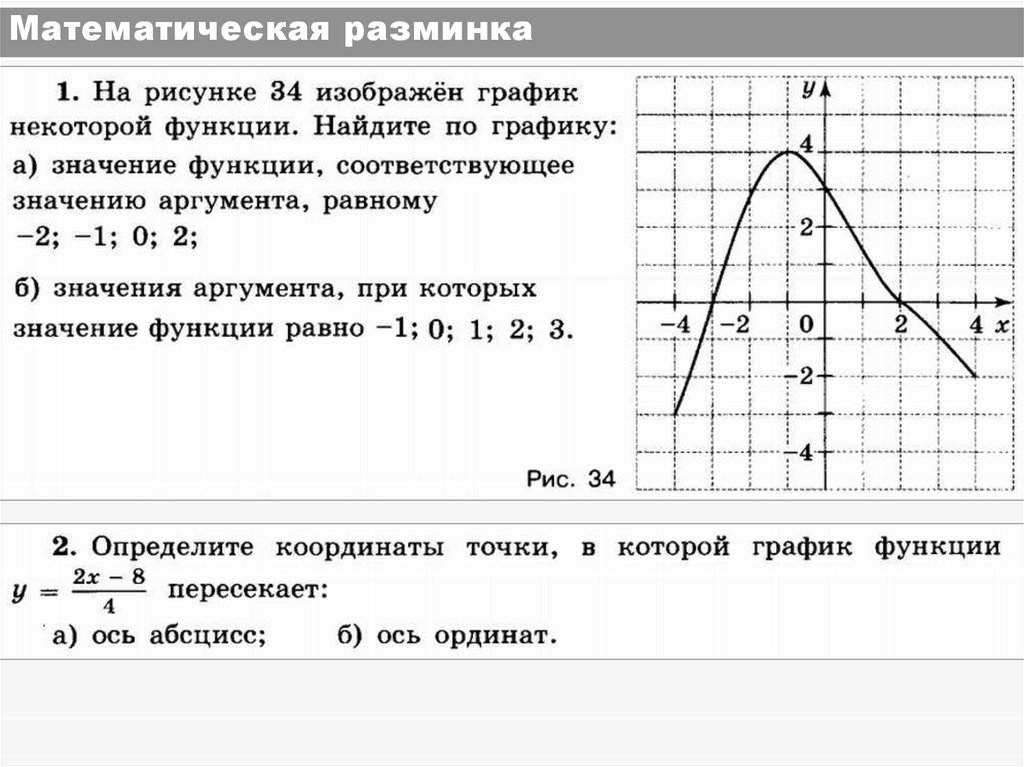
3. Математическая разминка

4. Свойства функции

Стр.252
Работа с учебником
Пример
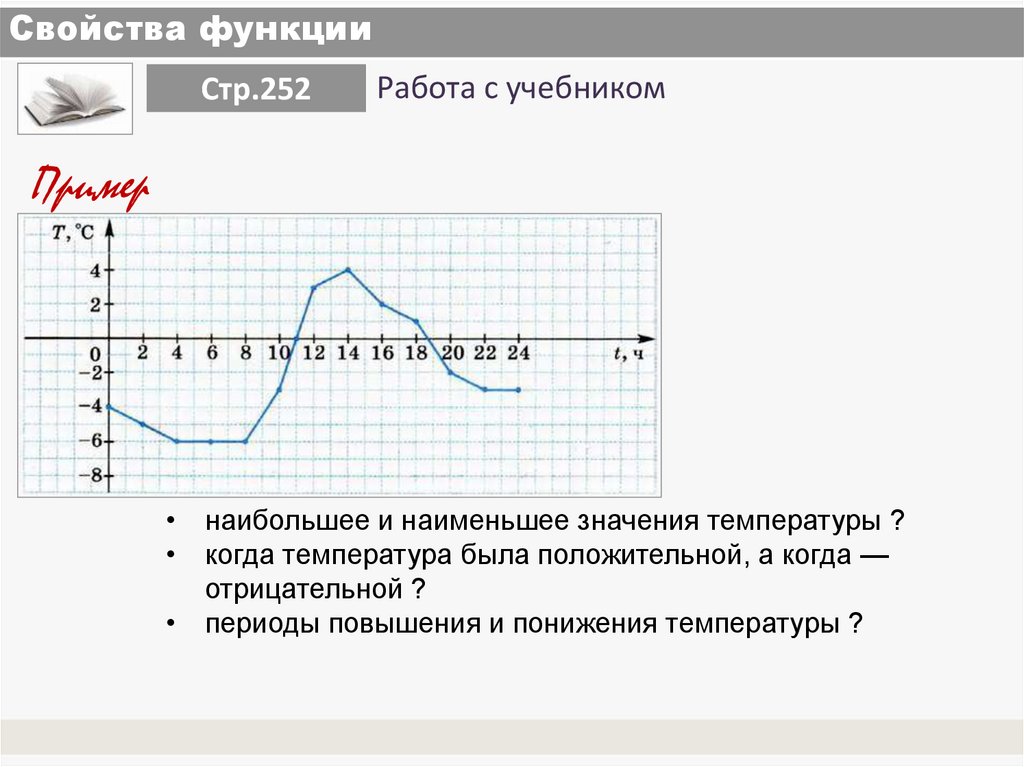
• наибольшее и наименьшее значения температуры ?
• когда температура была положительной, а когда —
отрицательной ?
• периоды повышения и понижения температуры ?

5. Свойства функции

Стр.252
Работа с учебником
график всякой функции, являясь её геометрическим
изображением, наглядно отражает все её свойства.
у функции у = f(x) есть наибольшее и наименьшее
значения.
Значения аргумента, при которых функция
обращается в нуль, называют нулями функции.
на промежутках (-4; -2) и (4; 8) значения функции положительны, а на
промежутке (-2; 4) значения функции отрицательны.
на промежутке [-4; 2] функция убывает.
на промежутке [2; 6] функция возрастает.

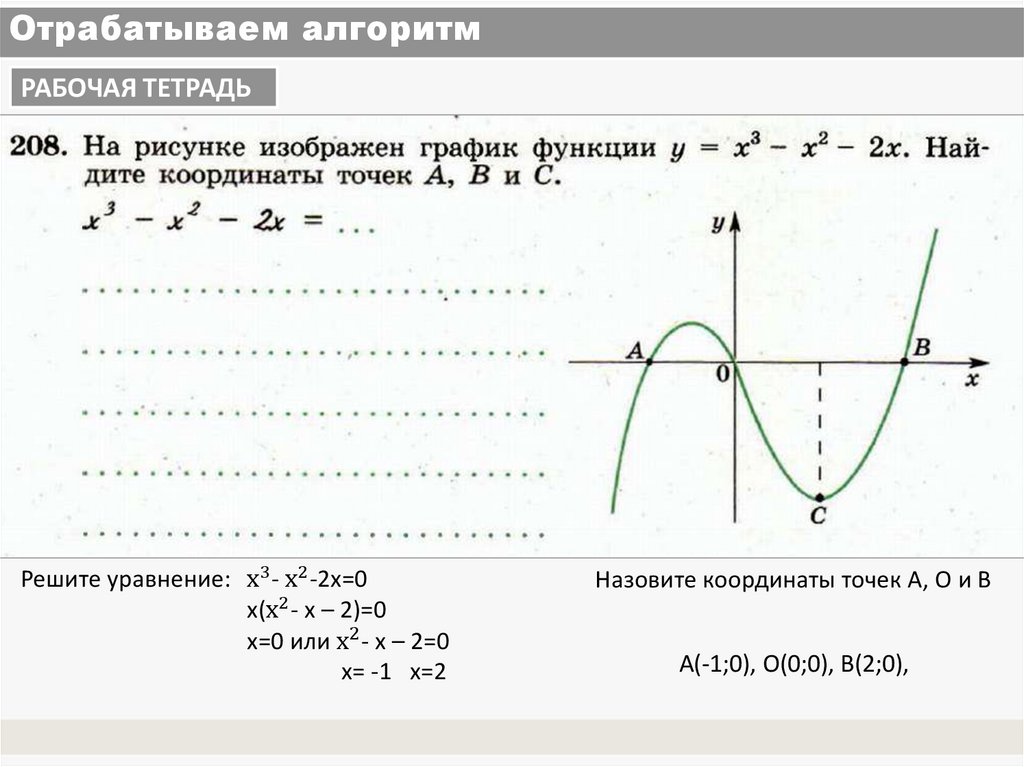
6. Отрабатываем алгоритм

РАБОЧАЯ ТЕТРАДЬ
Решите уравнение: х3 - х2 -2х=0
х(х2 - х – 2)=0
х=0 или х2 - х – 2=0
х= -1 х=2
Назовите координаты точек А, О и В
А(-1;0), О(0;0), В(2;0),

7. Отрабатываем алгоритм

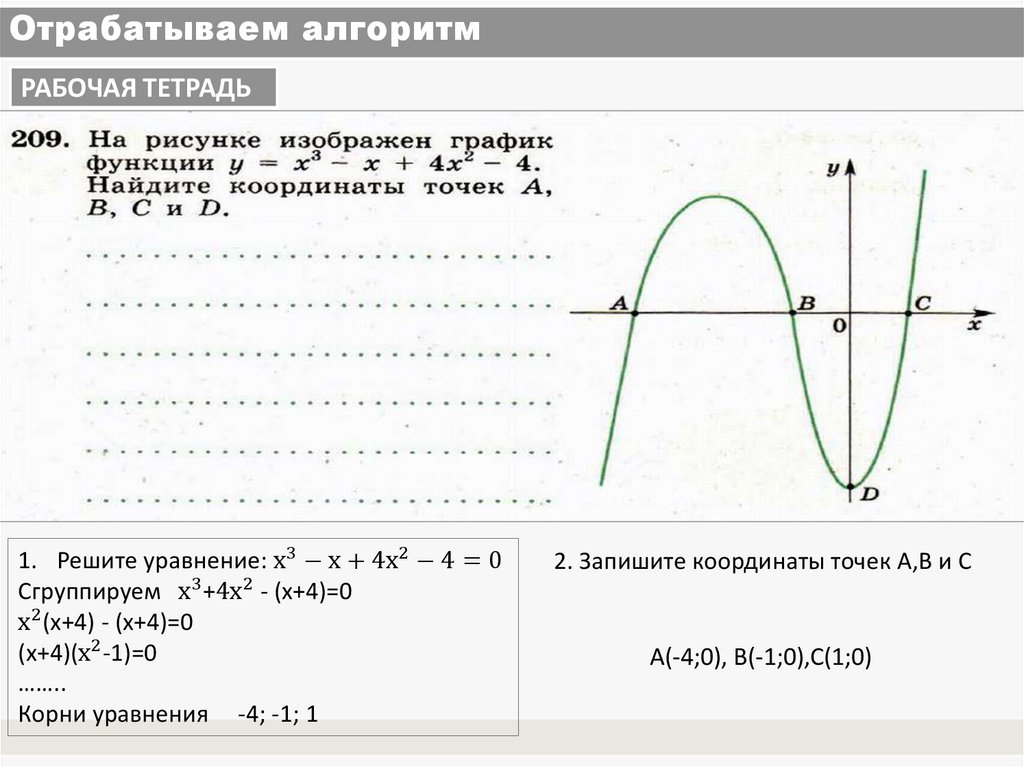
РАБОЧАЯ ТЕТРАДЬ
1. Решите уравнение: х3 − х + 4х2 − 4 = 0
Сгруппируем х3 +4х2 - (х+4)=0
х2 (х+4) - (х+4)=0
(х+4)(х2 -1)=0
……..
Корни уравнения -4; -1; 1
2. Запишите координаты точек А,В и С
А(-4;0), В(-1;0),С(1;0)

8. Отрабатываем алгоритм

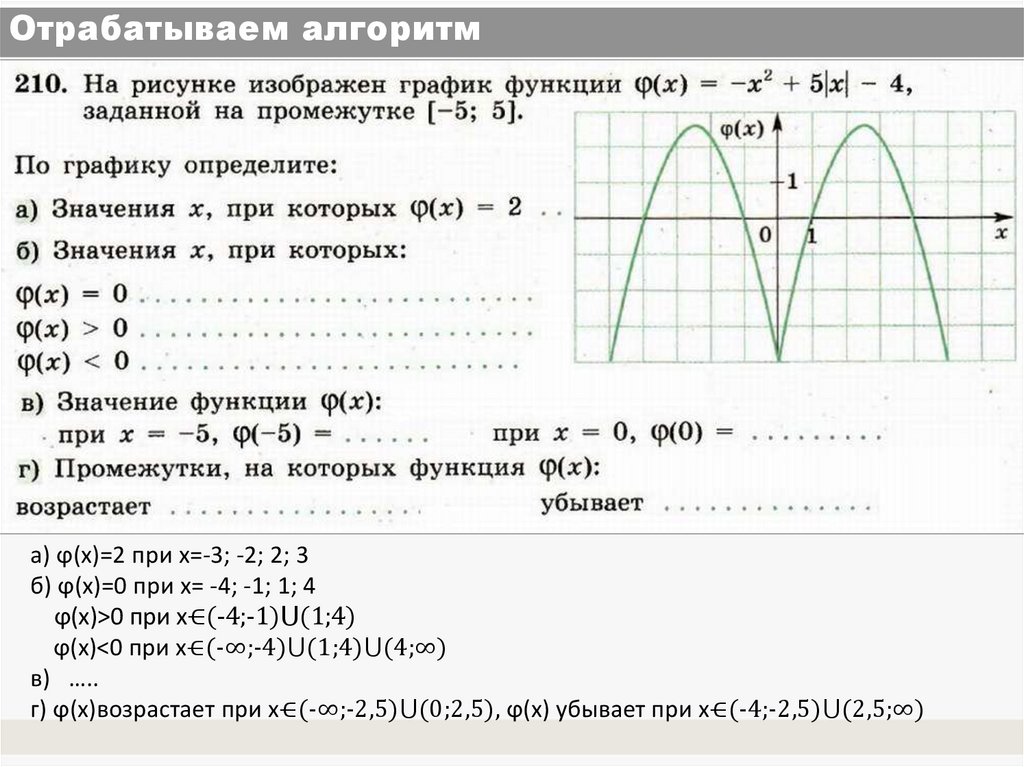
а) ϕ(х)=2 при х=-3; -2; 2; 3
б) ϕ(х)=0 при х= -4; -1; 1; 4
ϕ(х)>0 при х⋲(-4;-1)⋃(1;4)
ϕ(х)<0 при х⋲(-∞;-4)⋃(1;4)⋃(4;∞)
в) …..
г) ϕ(х)возрастает при х⋲(-∞;-2,5)⋃(0;2,5), ϕ(х) убывает при х⋲(-4;-2,5)⋃(2,5;∞)

9. Отрабатываем алгоритм

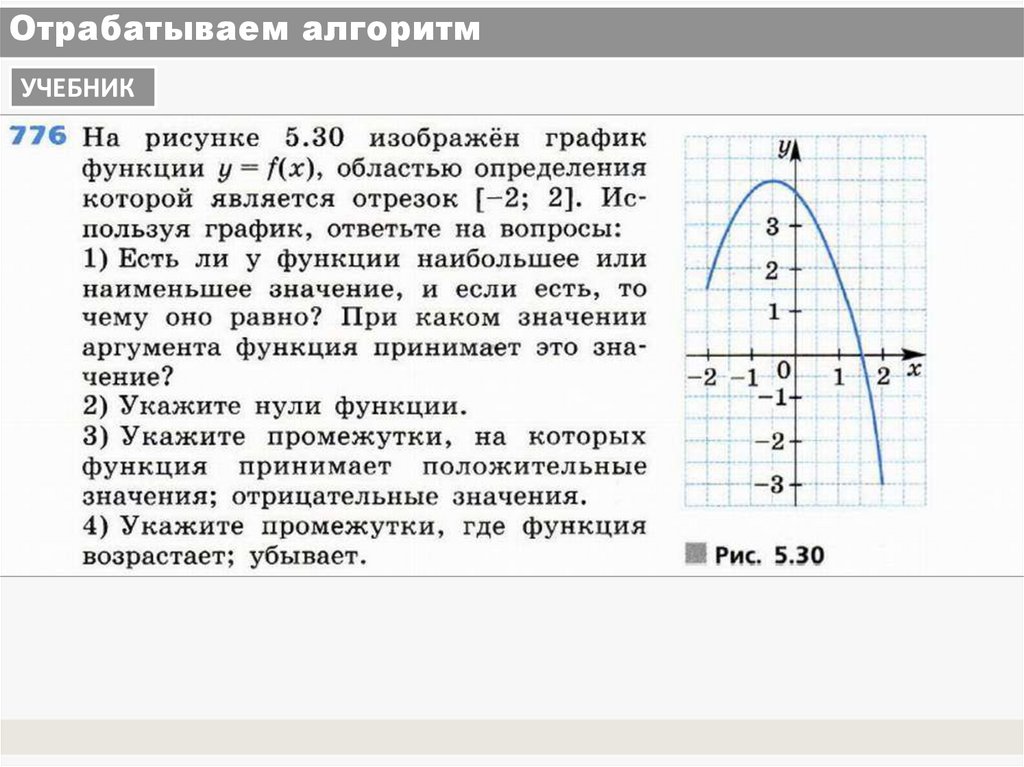
УЧЕБНИК

10. Отрабатываем алгоритм

УЧЕБНИК
2
3
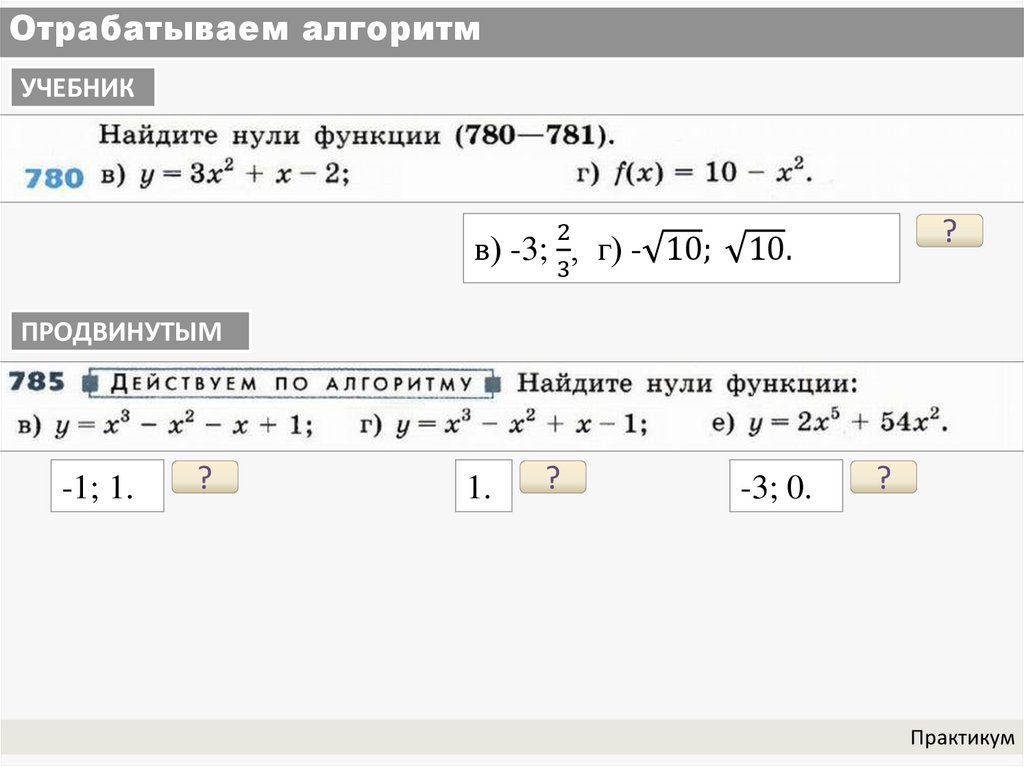
в) -3; , г) - 10;
?
10.
ПРОДВИНУТЫМ
-1; 1.
?
1.
?
-3; 0.
?
Практикум

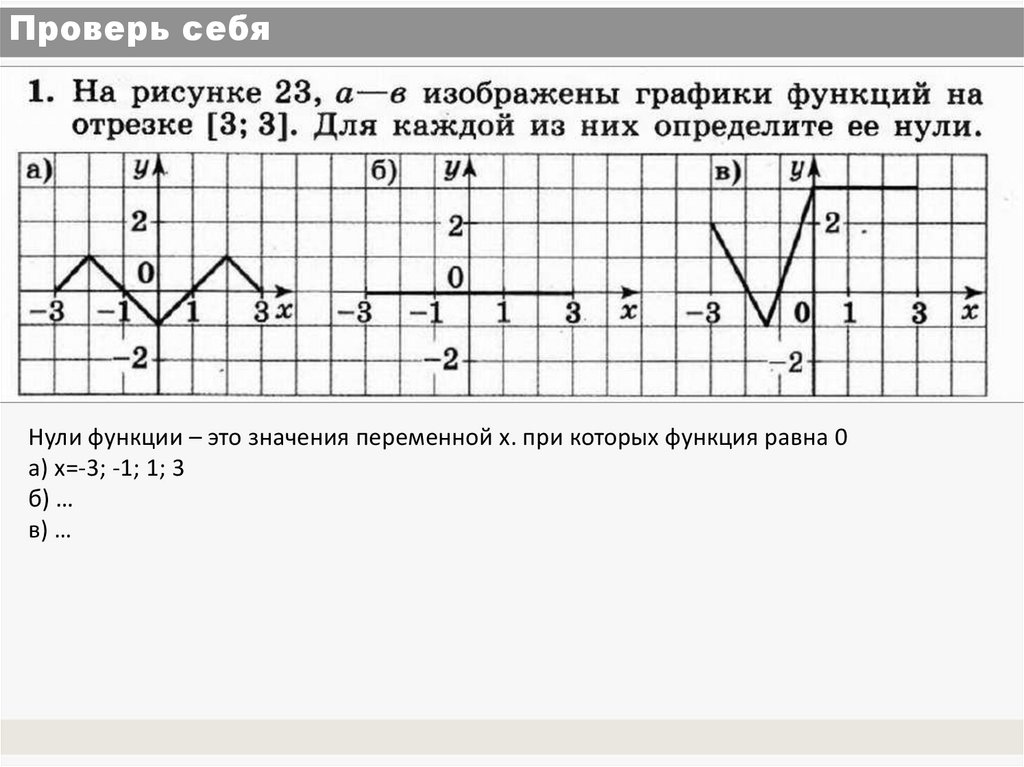
11. Проверь себя

Нули функции – это значения переменной х. при которых функция равна 0
а) х=-3; -1; 1; 3
б) …
в) …

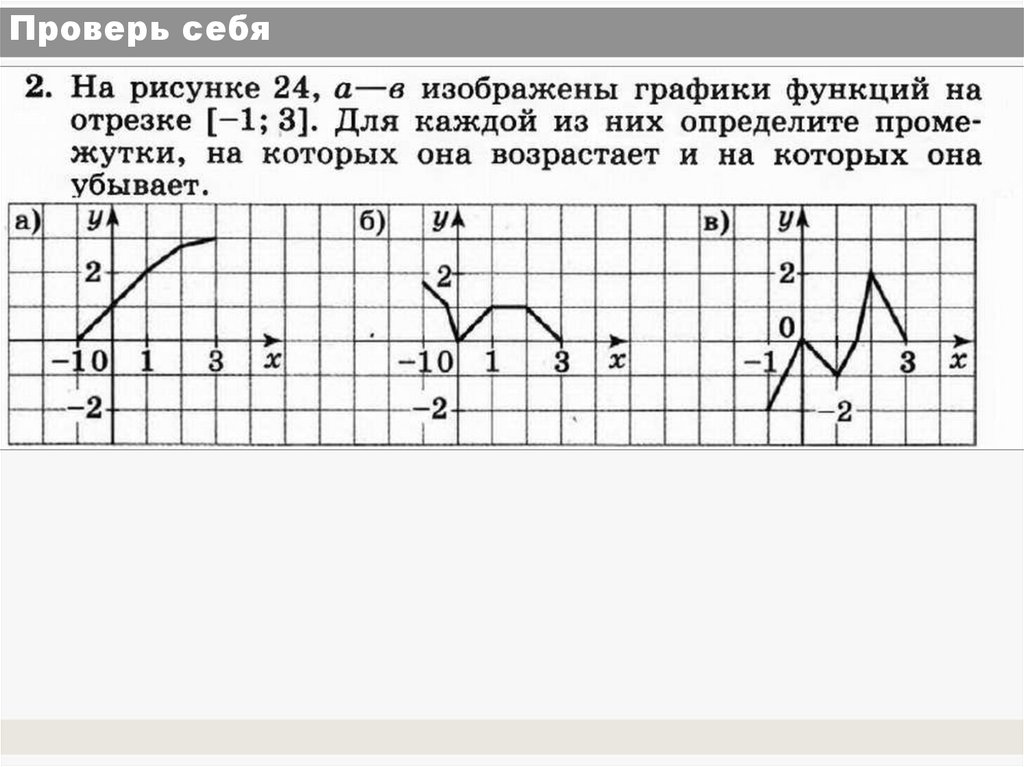
12. Проверь себя

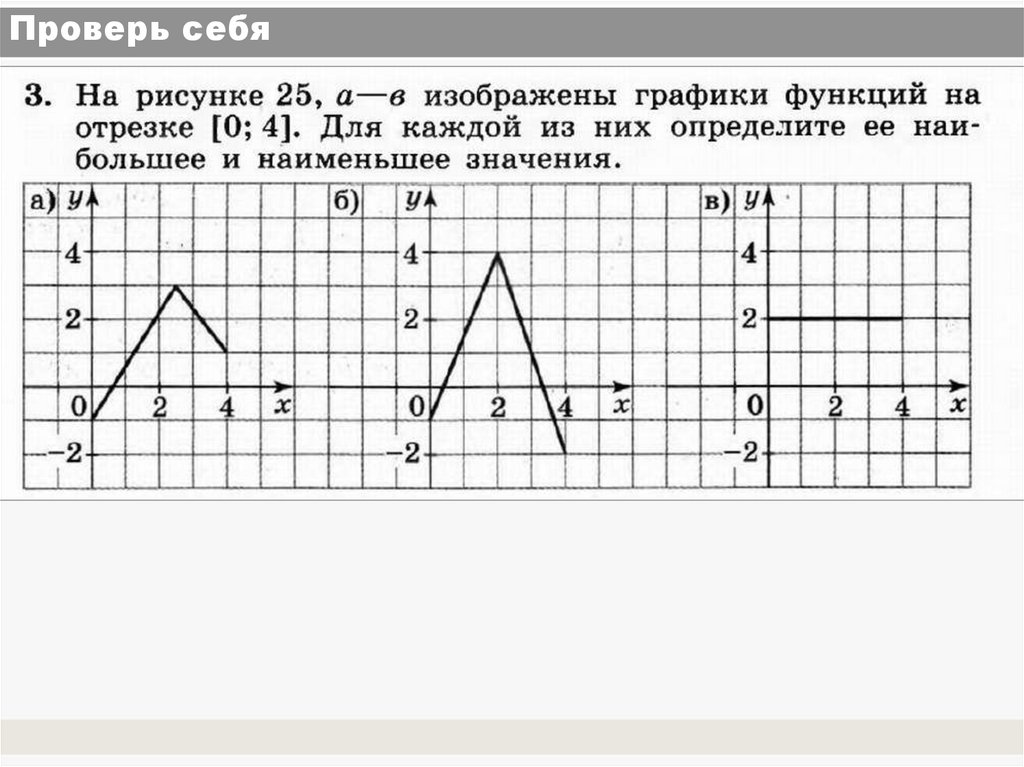
13. Проверь себя

14. Проверь себя

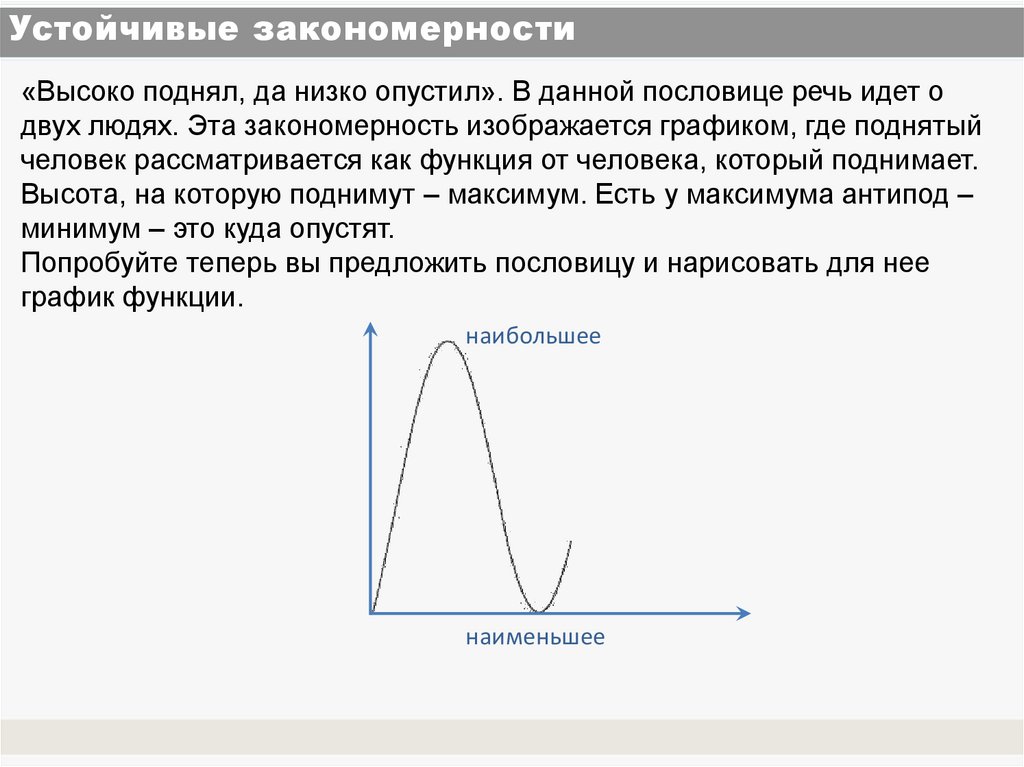
15. Устойчивые закономерности

«Высоко поднял, да низко опустил». В данной пословице речь идет о
двух людях. Эта закономерность изображается графиком, где поднятый
человек рассматривается как функция от человека, который поднимает.
Высота, на которую поднимут – максимум. Есть у максимума антипод –
минимум – это куда опустят.
Попробуйте теперь вы предложить пословицу и нарисовать для нее
график функции.
наибольшее
наименьшее