Similar presentations:
Геометрическая прогрессия
1.
Геометрическаяпрогрессия
2.
Геометрическая прогрессия – это числоваяпоследовательность, первый член которой
отличен от нуля и каждый член, начиная со
второго равен предыдущему умноженному
на одно и тоже не равное нулю число .
b1 , b2 , b3 ,..., bn ,... -геометрическая прогрессия,
если для всех натуральных n выполняется равенство
bn 1 bn q bn 0 q 0
q -знаменатель геометрической прогрессии (число)
3.
b1 , b2 , b3 ,..., bn ,...-геометрическая прогрессия
bn 1 bn q
bn 1
q
bn
знаменатель
геометрической прогрессии
(число)
q b2 :b1
q b3 :b2
q b4 :b3
4.
Формула n-го членагеометрической прогрессии
bn b1 q
n 1
5.
Свойство n-го членагеометрической прогрессии
b bn 1 bn 1
2
n
6.
Свойство n-го членагеометрической прогрессии
b bn 1 bn 1
2
n
Если все члены прогрессии положительны, то
каждый член геометрической прогрессии,
начиная со второго, равен среднему
геометрическому двух соседних с ним членов.
bn bn 1 bn 1
7.
Дома: Разобрать примеры 3 и 4 пункта 4.4Решить №641, №648(а) см.пример 1. Подсказка: знаменатель
q = 4/5 . Найти 5-ый член геометрической прогрессии. Реши
№652 см. пример 4. Подсказка: Найти по формуле хотя бы
первые три члена последовательности



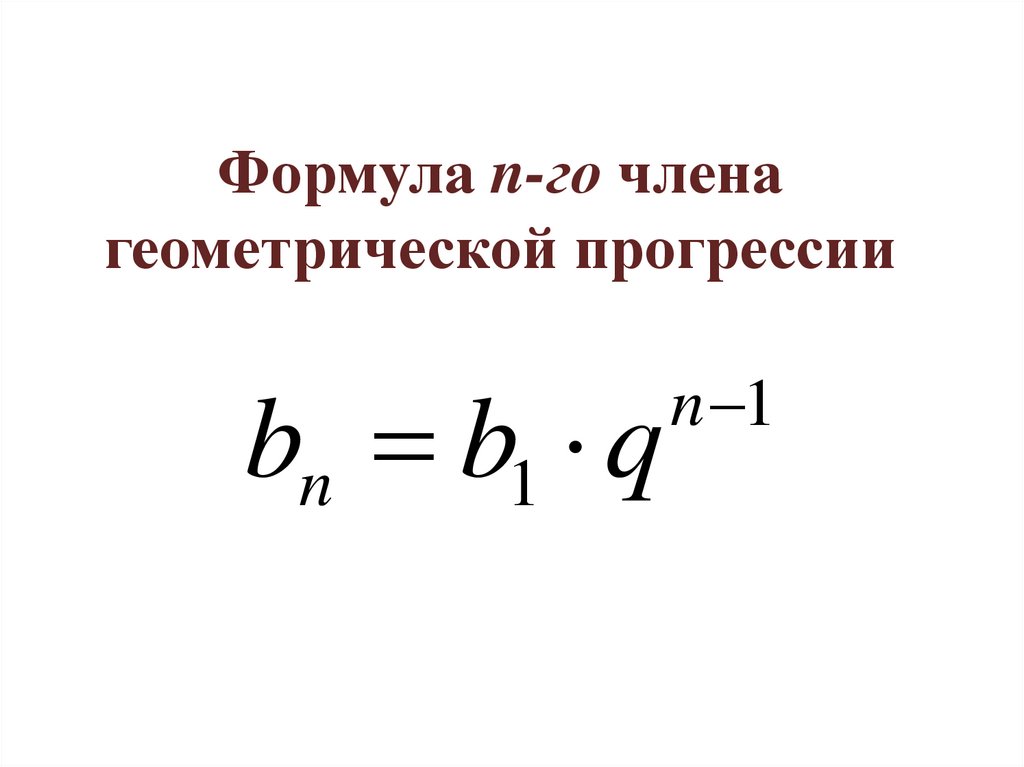
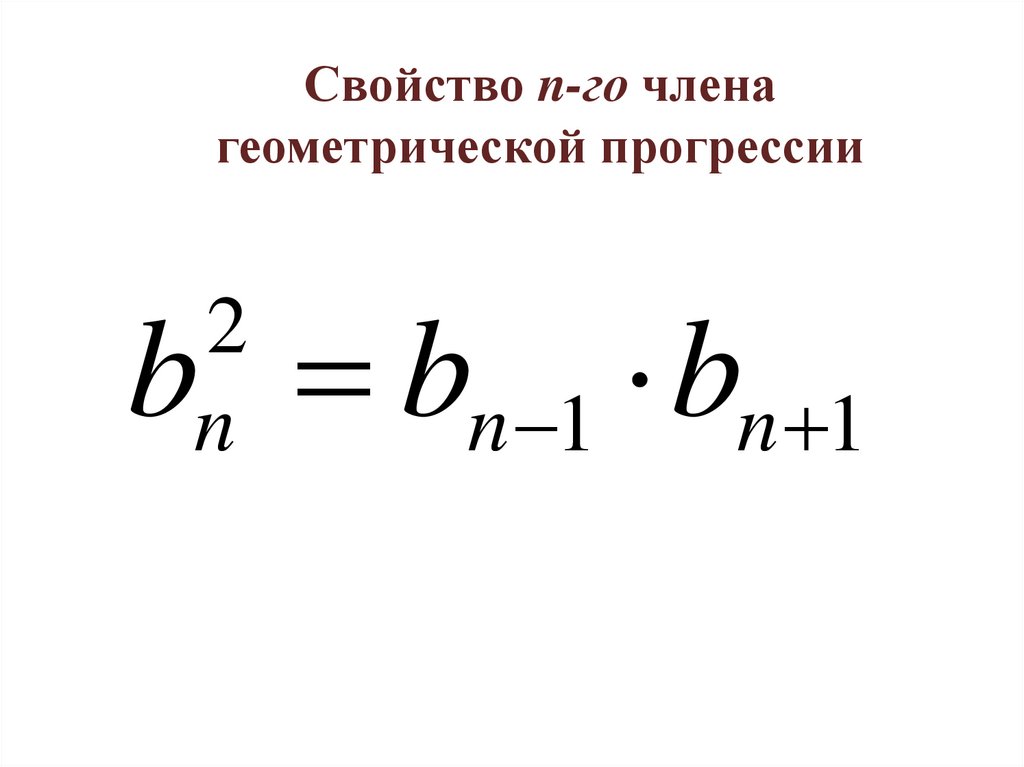


 mathematics
mathematics








